基于MATLAB的GPS周跳探测与修复
2021-11-18曹小鸿
曹小鸿
(三和数码测绘地理信息技术有限公司,甘肃 天水 741000)
GPS导航定位可以通过伪距和载波相位实现,而伪距的测量精度低于载波相位的精度,所以在高精度定位中一般用载波相位测量实现。而载波相位是由整周部分和不足一周的小数部分构成,整数部分的连续变化值可以通过多普勒计数得到,载波相位只能测量相位中小于一周的值,但如果在测量过程中信号受到遮挡、信噪比低以及接收机出现故障等情况都会导致整周计数部分发生突变,即发生整周跳变的现象[1-4],简称为周跳(cycle slip)。由于周跳在GPS高精度定位中影响特别大,所以必须进行修复。
1 周跳探测原理
GPS观测量是一种时间序列,周跳是GPS载波相位观测数据序列中的一种粗差。探测GPS载波相位观测量是否存在周跳,就是发现其是否发生突变,即通过比较观测量在相邻历元间的变化是否连续,从而判断周跳的位置和大小。周跳探测的方法比较多,各有优缺点[5-7]。本文主要介绍电离层残差法和Melbourne-Wübbena组合法。
1.1 电离层残差法
电离层残差法由Goad在1986年提出,利用双频载波相位测量的电离层残差进行探测和修复周跳[8]。它主要利用不同历元电离层误差的变化。在不考虑多路径效应和其他测量噪声的条件下,同一历元的双频载波相位测量值差为:
φ(t)=λ1φ1(t)-λ2φ2(t)
(1)
式中,t为观测时刻;φ1(t)和φ2(t)为L1和L2两个频率的载波相位;λ1和λ2为L1和L2两个频率对应的波长;N1和N2为L1和L2两个频率的整周未知数;f1和f2为L1和L2两个频率对应的频率;A(T)为其他项。将式(1)两端同除以λ1,则有:
(2)

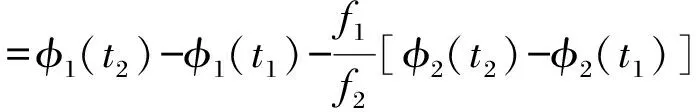
=Δion(t2)-Δion(t1)+ε
(3)
当电离层变化不大时,检测量D1的值会在0附近上下波动。若存在周跳,令ΔN1、ΔN2分别为L1、L2的周跳值,如式(4)所示:
(4)
1.2 Melbourne-Wübbena组合法
Melbourne-Wübbena组合法是由Melbourne和Wübbena提出的,简称M-W组合法[9-10]。由于M-W组合的波长约为86 cm,因为波长较长对探测周跳特别有利。M-W组合法是载波相位宽巷组合减去测码伪距窄巷组合,因此,其组合观测值如下:
(5)
式中,P1和P2为伪距观测值;L1和L2为载波相位观测值;f1和f2为对应的频率;λ1和λ2为对应的波长。则M-W组合的宽巷整周模糊度为:
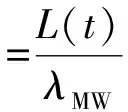
(6)
则M-W组合法周跳检测量D2为:
D2=N(t2)-N(t1)
(7)
1.3 电离层残差法和M-W组合法组合探测周跳
由于当L1和L2周跳比值为77/60时,电离层残差法无法探测出周跳,但M-W组合法可以探测出周跳;当L1和L2周跳比值为1时,M-W组合法无法探测出周跳,但电离层残差法可以探测出周跳。则可以采用电离层残差法和M-W组合法组合起来探测周跳,联立式(4)和式(6)得方程组:
(8)
则周跳值N为:
(9)
至此,GPS周跳发生的位置和大小可以求得。
2 算法实现
2.1 数据预处理
本文探测周跳的数据选择国内IGS站的SHAO站,由于MATLAB软件在数据处理方面有着特别强大的功能,编写了读取O文件的程序,然后,根据探测周跳的方法完成了程序的编写,电离层残差法和M-W组合法组合探测周跳方法核心代码如下:
f1=1575.42*10^6; %f1的频率
f2=1227.60*10^6; %f2的频率
C0=299792458; %光速
b1=C0/f1; %f1对应的波长λ1
b2=C0/f2; %f2对应的波长λ2
b3=C0/(f1-f2); %宽巷组合对应的波长λ3
for k=1:1:t
MW(k,1)=Obs_L1(k)-Obs_L2(k)-(f1*Obs_P1(k)+f2*f1*Obs_P2(k))/(b3*(f1+f2));
end
for j=1:1:(t-1)
GFMW(j,1)=Obs_L1(j+1)-Obs_L1(j)-(f1/f2)*(Obs_L2(j+1)-Obs_L2(j));
GFMW(j,2)=MW(j+1,1)-MW(j,1);
end
A1=[1 -f1/f2;1 -1];
D1=GFMW(1:t-1,1:2);
CycleJump(1:t-1,1:2)=((inv(A1))*D1')';
CycleJumpFix=fix(CycleJump (1:t-1,1:2));
实验选取了该站10号GPS卫星200个观测历元的连续观测数据,先对该200个历元的观测数据进行周跳探测与修复,形成一组无周跳的观测数据,然后,根据各种方法的优缺点人为的加入周跳,接着进行周跳探测,处理过的周跳图如图1所示。
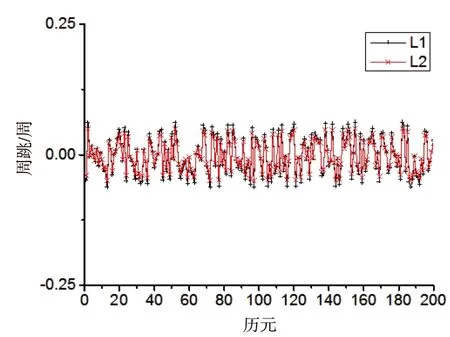
图1 无周跳的原始数据
2.2 周跳探测
根据不同方法的优缺点,人为的对L1和L2加入不同的周跳值,然后,分别用每种方法进行周跳探测,加入的周跳数如表1所示。

表1 周跳探测与修复结果
分析图2数据和表1内容,将人为加入的周跳值通过两种组合方法进行探测。因为小周跳探测比较困难,所以在第20和第50历元处对L1和L2分别加入了周跳值为1,探测结果也比较理想,探测结果残差值均较小(小于0.05周),取整后的结果完全一致,完全实现了小周跳的探测。在第80和第100历元处对L1和L2都加入较小的周跳值,再次验证组合方法对较小周跳的适用程度,残差值为0.01周,取整后的结果完全一致,结果表明组合方法对较小周跳完全适用。由于当L1和L2周跳比值为77/60时,电离层残差法无法探测出周跳,但M-W组合法可以探测出周跳,所以在第140历元的时候,在L1上加入了77周,L2上加入了66周,进行组合法探测,探测结果是正确的。当L1和L2周跳比值为1时,M-W组合法无法探测出周跳,但电离层残差法可以探测出周跳,在第170历元处对L1和L2都加入50周,探测结果残差值均小于0.05周,取整后的结果完全一致,周跳探测结果理想,证明组合法既对大周跳探测准确,又对L1和L2周跳比值为1的时候周跳探测是有效的。本文研究重点为通过人为模拟实验进行周跳探测,该方法对定位结果影响程度分析将在后续具体的实测数据中进行分析,本文将不再进行讨论。

图2 周跳探测结果
2.3 周跳修复
根据探测出周跳值和所在的位置,计算发生周跳的历元处的累计周跳值,然后,对两个频率的载波相位观测值进行修复,修复结果如图3所示。根据修复结果,再进行周跳探测,分析表明,未探测出明显周跳,说明修复效果较为理想,基本修复了人为加入的周跳。
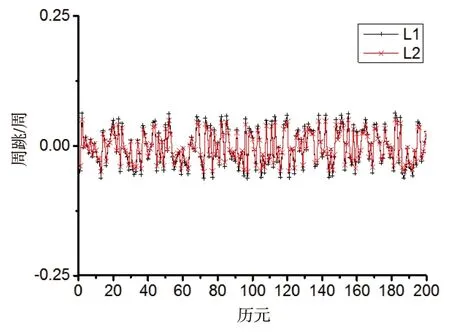
图3 修复完成后的周跳探测图
3 结 论
由于周跳在GPS精密定位中对定位精度影响极大,因此,在数据处理前必须先探测和修复周跳,由电离层残差法和M-W组合法组合成的方法可以避开这两种方法的缺点,利用其优点相互补充,可以实现载波相位发生的各种大小和任意比例周跳的探测,从而提高GPS精密定位的定位精度。
猜你喜欢
——记叙文选材组材创新方法之三
