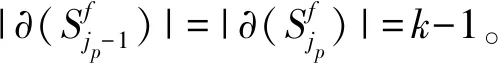k-割宽图的一个结构性质
2021-11-18张振坤叶希琼庞留勇
张振坤,叶希琼,庞留勇
(1.黄淮学院 河南 驻马店 463000;2.郑州电子信息工程学校 河南 郑州 450007)
0 引言
本文所考虑的图均为简单有限的连通图,文中图论概念均来源于文献[1]。自20世纪80年代图的标号(又称图的嵌入)问题提出以来,因为图的割宽与微电子芯片电路布线中一个称为“拥塞度(congestion) ”的基本物理参数密切相关[2-4],所以有学者对图的割宽问题展开深入研究。简明地,设G=(V(G),E(G))是一个具有n=|V(G)|个顶点的图,Pn=x1x2…xn是一个具有n个顶点的路,其中V(G)={vi:1≤i≤n}为G的顶点集,E(G) ={vivj:1≤i,j≤n}为G的边集,xj(1≤j≤n)是Pn的顶点,将G的每个顶点vi分别嵌入到路Pn的相应一个顶点xj上(简称G到Pn的一个嵌入),使得Pn上每一对连续的顶点xj,xj+1之间重叠的边数达到最小,这个最小边数就称为图G的割宽,表示为c(G)。这里的图G可以看成是一个微电子芯片的电路布线示意图,vi表示芯片电路板上的节点,边vivj表示连接节点vi,vj的电线。当这个电路安装在Pn上时,Pn上所有连续的顶点xj,xj+1之间重叠的电线根数的最大值就称为这个嵌入的拥塞度(congestion),这是一个度量电路性能的基本物理参数,是图论中割宽问题的主要物理背景。同时,图的割宽问题与超大规模集成电路、网络通信等实际问题也有关联[2,3,5,6]。理论上,图的割宽还与其他一些图论参数,如图的带宽、路宽、树宽等紧密相关[3, 7, 8]。
对一般图G来说,割宽的计算问题是NP-困难的[9], 即使G是最大度为3的平面图[10]。因此,自图的嵌入问题提出以来,确定在多项式时间内割宽可计算的图类及其结构特征一直是该问题的主要研究内容。然而,由于该问题的难度较大,所以取得的科研成果相对较少。目前,仅有的研究成果包含以下几个方面。算法方面,Chung和Makedon等人于1982年首先得到了计算最大度为d≥ 1的树的割宽的O(n(logn)d-2)算法[11]。1985年,Yannakakis在文献[12]中改进了这各个结果,并给出了计算任意树的割宽的多项式O(nlogn) 算法。其他的割宽可在多项式时间内计算的特殊图类有超立方体[13]、d-层树的r-维网格[14]、循环毛虫树[15]、完全二部图Km,n、格子图Pm×Pn,Pm×Cn,Cm×Cn和一些乘积图Km×Pn,Km×Kn,Pm⊗Pn[16],其中Km、Cm分别表示具有m个顶点的完全图和圈。k-割宽图的结构研究方面,文献[17]得到了4-割宽图的所有5个禁用子图,文献[18]给出了5-割宽树的所有18个禁用子图以及一些特殊的k-割宽树的禁用子图(k≥ 5), 文献[19]刻画了一般的k-割宽树的可分解性质(k≥4)。另外,Chung和Makedon 等人[11]于1982年给出了k-割宽树的特殊结构。本文将Chung和Makedon 等人的结果推进到了一般图的情形,证明了如下结果:对图G任意度数大于或等于3的点v∈D≥3(G), 假设Vi(1 ≤i≤m)为G-v的一个连通分支的一个点集,子图Hi=G[Vi∪{v}]。那么,c(G) ≤k当且仅当c(G(v;NHi(v),NHj(v)))≤k-1 (1 ≤i,j≤m)且v的邻点集NG(v)中至少存在两个点v1,v2使得vv1,vv2是G的割边。利用这个性质,本文研究了一类割宽为k的临界图的结构。
1 基本知识
对整数n>0,设集合Sn={1, 2, …,n},图G= (V(G),E(G)),其中V(G) = {vi: 1 ≤i≤n}为G的顶点集,E(G) = {vivj: 1 ≤i,j≤n}为G的边集,|V(G)| =n。Pn是一条具有n个顶点的路。
定义1.1图G的点集V(G)到Sn的一个映射f:V(G) →Sn称为图G的一个标号,也称为由f导出的G到路Pn的一个嵌入。
定义1.2如果
c(G,f)=max1≤j (1) 则称c(G,f)为图G关于标号f的割宽(或拥塞度)。 定义1.3图G的割宽是 c(G)=minfc(G,f), (2) 这里的最小值指的是取遍所有标号f的最小值。如果k=c(G,f), 则f以及由f导出的G到路Pn的一个嵌入称为G的k-割宽嵌入。在式(2)中取得最小值的标号f称为最优标号。例如,图1(a)是一个3-割宽图G,图1(b)中的标号是G的一个最优标号, 而图1(c)中的标号就不是G的一个最优标号。 图1 一个3-割宽图G和它的两个标号 (3) 对图G和整数i≥ 1,令Di(G) = {v∈V(G) :dG(v) =i},其中dG(v)表示点v∈V(G)的度数,D1(G)的任意点v称为G的悬挂点。设e是G的一条边,如果G-e包含至少两个连通分支,则称e是G的一条割边。对任意v∈V(G),NG(v) = {u∈V(G) :uv∈E(G)}称为v的邻点集。对V'⊂V(G)且V′≠∅, 则G[V′]称为V′的导出子图,且G[V(G)V′]=G-V′。如果V′={v},我们将用G-v代替G-{v}。相似地,G-E′表示从G中删除边集E′后所得到的图,且如果E′={e}则G-{e}将表示为G-e。如果v∈D2(G),NG(v) = {v1,v2}且v1v2∉E(G),则称G-v+v1v2为图G的一个序列缩减,该图表示在图G-v中添加一条新边v1v2。如果一个图不能进行任意序列缩减,则称G是同胚极小的。如果两个不相交的图G和G′都是同一个图H的序列缩减,则称G和G′是同胚的。 定义1.4设图G的割宽是k, 如果G满足(1) 对G的任意子图G′,c(G′) 根据定义,引理1.5是显然的。 引理1.5设G和G′是两个图, 则下列两个结论成立。 (1) 如果G′是G的一个子图,则c(G′)≤c(G); (2) 如果G′和G是同胚的,则c(G′)=c(G)。 作为极图理论的重要内容之一,k-割宽临界图在刻画割宽为k的图的结构特征方面具有重要的理论意义。在第三节,本文刻画了一类k-割宽临界图。 首先,对于整数n≥ 1,令P是一条路,其点集V(P) =Sn,且对任意1 ≤i 如果e∈E(G), 则c(G-e) ≤c(G)。 (4) 定义2.1(i) 对整数r≥ 1,设v0是G的度数dG(v0) >r的一个顶点,v1,v2, …,vr∈NG(v0), 则称G(v0;v1,v2, …,vr)为G-{v1,v2, …,vr}的一个包含v0但不包含点v1,v2, …,vr的连通分支(见例子图2(a))。 图2 定义2.1(i)的例子和定义3.1(ii)的示例图 (ii) 设|E(G)| ≥ 2, 则称M(G) = {G-e:e是G的一条悬挂边,或e∈E(Ct)}为G的所有不包含孤立点的极大真子图的集合,其中Ct表示G的长度为t(t≥3)的一个圈(见公式(4))。 引理2.2设f是G的一个最优标号,f(x) = 1,f(y) = |V(G)|,Px,y是在f下连接x,y的一条路。如果存在某个i0,c(Hi0)=β,且对任意v∈Vi0,v∉V(Px,y)和f(v)≠1,|V(G)|,则c(G)≥β+1。 证明:因为对任意点v∉Vi0,v∈/V(Px,y),所以x,y∉Vi0。同样地,由Hi0是G的一个连通分支知,对任意点u∈V(Px,y) {x,y},u∉Vi0。 这样,V(Px,y) ∩Vi0= ∅, 并且无论v0是否属于V(Px,y),Px,y在f下完全越过Hi0。因此,c(G)≥c(Hi0)+1=β+1。 引理2.3设v1,v2∈NG(v0),v0v1和v0v2是G的割边,c(G[V1]) ≤k-1,c(G[V2]) ≤k-1,c(G(v0;v1,v2))≤k-1,则c(G)≤k。 定理2.4对任意v∈D≥3(G), 设Vi(1 ≤i≤m)是G-v的一个连通分支的顶点集,Hi=G[Vi∪ {v}],则下列论断是等价的。 (i)c(G) ≤k; (ii) 对任意1 ≤i,j≤m,c(G(v;NHi(v),NHj(v)))≤k-1, 并且NG(v)中至少存在两个点v1,v2使得vv1,vv2是G的割边。 证明:(⟹) 反证法。假设(i)成立但是G中存在至少一个点v′∈D≥3(G)使得(ii)不成立,也即是说,对任意H′i=G[V′i∪{v′}],H′j=G[V′j∪{v′}],c(G(v′;NHi′(v′),NHj′(v′)))>k-1,其中V′i,V′j分别为G-v′的两个连通分支的顶点集。设f:V(G)→{1,2,…,n}是G的一个标号,c(G,f) =k,并令x,y∈V(G),f(x) = 1,f(y) =n,P是在标号f下连接x和y的一条路。我们考虑两种情形。 情形1:v′∈V(P)。 情形1.1:v′∉{x,y}。根据假设,令v′1,v′2∈NG(v′)∩V(P),NH′i(v′)={v′1},和NH′j(v′)={v′2}。也即是说,i=1,j=2且v′v′1,v′v′2是G的割边。则由已知,G(v′;NH′1(v′),NH′2(v′))=G(v′;v′1,v′2),G(v′;NH′1(v′))=G(v′;v′1),G(v′;NH′2(v′))=G(v′;v′2),且c(G(v′;v′1,v′2))>k-1。由于v′是P的内点,且v′1,v′2∈NG(v′),我们可设f(v′1)=min{f(v):v∈V(G(v′;v′1,v′2))}-1和f(v′2)=max{f(v):v∈V(G(v′;v′1,v′2))}+1。这样,如图3(a)所示,P=x…v′1v′v′2…y,且在f下P完全越过图G(v′;v′1,v′2)。 因此,由引理2.2,k=c(G,f)≥c(G)≥c(G(v′;v′1,v′2))+1,矛盾。同样地,如果v′1,v′2有一个属于V(P)或者v′1,v′2均不属于V(P),我们仍然可以得到同样的矛盾。事实上,如果v′1∈V(P),v′2∉V(P), 则P完全越过子图G(v′;v′2),进而由于G(v′;v′1,v′2)⊂G(v′;v′2),P完全越过图G(v′;v′1,v′2)(见图3(a))中的路P=x…v′1v′…y′)。对于v′1∉V(P),v′2∉V(P)的情形,令x∈V(Gi)和y∈V(Gj),这里i,j∉{1,2}。则我们可以看到P完全越过G(v′;NH′i(v′),NH′j(v′)),也是一个矛盾。 图3 定理2.4的图示 情形1.2v′∈{x,y}, 比如,v′=y。与情形1.1相似,令v′1∈NG(v′)∩V(P),f(v′1)=min{f(v):v∈V(G(v′;v′1))}-1。则由f(v′)=f(y)=n, 路P在标号f下也完全越过G(v′;v′1),见图3(b)。这样,根据G(v′;v′1,v′2)⊂G(v′;v′1),c(G(v′;v′1))>k-1。进而可得k=c(G,f)≥c(G)≥c(G(v′;v′1))+1>k,与c(G)≤k矛盾。 情形1.3:v′1∉V(P),v′2∉V(P)。验证过程与情形1.1相似,这里省略。 情形2:v′∉V(P)。验证过程和情形1一样,我们仍然可以得到和c(G) ≤k不一致的矛盾,这里省略。因此,结论(ii)成立。 (⟸) 假设(ii)成立。在G中固定一个点v0,其邻点集NG(v0) = {v1,v2, … ,vp},并且假设v0v1,v0v2是G的割边, 即NH1(v0) = {v1},NH2(v0) = {v2},G(v0;NH1(v0),NH2(v0))=G(v0;v1,v2)。 由已知,c(G(v0;v1,v2))≤k-1。 令H′1=G(v0;v2,v3,…,vp)-v0,H′2=G(v0;v1,v2),H′3=G(v0;v1,v3,…,vp)-v0。 (5) 证明完成。 推论2.5[3]设T是一个树,c(T)≤k当且仅当对T的任意度数大于或等于2的点v,总存在两个点v1,v2∈NT(v)使得c(T(v;v1,v2))≤k-1。 式(5)中的标号f称为f是由顺序(f1,f2,f3)或(V(H′1),V(H′2),V(H′3))定义的。 推论2.6设v是G的一个点,v∈D≥3(G),如果对任意1 ≤i,j≤m,c(G(v;NHi(v),NHj(v)))≥k-1成立,则c(G) ≥k,即使NG(v)包含两个点vi,vj使得vvi,vvj是G的割边。 由定理2.4, 我们可得到一类k-割宽临界图。根据文献[18],由于K1,2k-1是k-割宽临界的,在本节中我们约定对任意v∈V(G),其度数dG(v)≤2k-2。 定义3.1(i) 设G,H是两个不相交的图,u∈V(G),v∈V(H)。把u和v粘合成一个点z就是用一个新点z代u和v(即u=v=z), 且z分别和G中u的所有邻点、H中v的所有邻点均相连。这种运算得到的图表示为G⊙u,vH,即G⊙u,vH=(G-u)∪(H-v)∪{zw:w∈NG(u)∪NH(v)}, 其中z称为粘合点。 (ii) 设G1、G2、G3是3个不相交的图,D3(K1,3) = {u0},D1(K1,3) = {u1,u2,u3}。 对每一 个1≤j≤3,令vj∈V(Gj)。定义K1,3⨁ (G1,G2,G3)为分别将每一对uj和vj粘合在一起所得到的图(见图2(b)中的示例)。 引理3. 2设G是一个图,D1(G)≠∅,Pl=x0x1…xl是一个长度为l的路。则对意v0∈V(G),c(G⊙v0,x0Pl)=k。 (6) 定理3.3根据定义3.1(ii), 如果{G1,G2,G3}有至少一个图, 比如说G2, 是(k-1)-割宽临界的,且D1(G2)≠∅, 那么c(K1,3⨁(G1,G2,G3))=k。 证明:令G=K1,3⨁ (G1,G2,G3)。对任意1≤j≤3,如果dG(vj) = 2, 即dGj(vj)=1,则根据引理1.5先对图G进行序列缩减。因为u0v2是子图G2⊙u2,v2u0v2的一条悬挂边且G2是(k-1)-割宽临界的,所以,根据引理3.2,c(G2⊙u2,v2u0v2)=k-1。 因为G-{u0v1,u0v3}包含3个割宽为k-1的连通分枝G1,G2⊙u2,v2u0v2,G3, 所以,相似于式(5),我们可以得到一个由(V(G1),G2⊙u2,v2u0v2,V(G3))确定的最优标号,f:V(G)→{1,2,…,n}且c(G,f) ≤ (k-1) + 1 =k。 因此,由式(2),c(G) ≤k。 另一方面, 由推论2.6,c(G) ≥k。 这是因为对任意vi,vj∈NG(u0),c(G(u0;vi,vj))=k-1。这样,c(G)=k。 推论3.4根据定义3.1(ii), 对每一个1≤j≤3, 如果Gj是(k-1)-割宽临界的,vj∈D1(Gj), 则K1,3⨁ (G1,G2,G3)是k-割宽临界的。 证明:令G=K1,3⨁ (G1,G2,G3)。对每一个1≤j≤3,因为dG(vj)=2,所以我们首先对G进行至少3次序列缩减。为方便,我们仍然令NG(u0) = {v1,v2,v3}。 这样G(u0;v1,v2) =G3,G(u0;v2,v3) =G1,G(u0;v1,v3) =G2, 并且由假设和定理3.3可得c(G)=k。 其次, 我们验证G的k-割宽临界性,即对任意G′∈M(G),c(G′)≤k-1。由定义2.1(ii),任意G′都可以通过删除G的一条边xy得到,这里的xy即可以是G的悬挂边,也可以是G的圈Ct(t≥ 3)中的非悬挂边,即xy∈E(Ct), 但xy∈/{u0v1,u0v2,u0v3}。不失一般性, 不妨令xy∈E(G2)。对每一个1≤j≤3,因为Gj是(k-1)-割宽临界的,所以,c(G1-u0v1) ≤k-2,c(G2-xy) ≤k-2和c(G3-u0v3)≤k-2。这样, 相似于式(5), 我们可以得到G′的一个由(V(G1-u0v1),V(G2-xy),V(G3-u0v3))定义的标号f′:V(G′)→{1,2,…,|V(G′)|},并且c(G′,f′)=k-1。因此,根据式(2),c(G′)≤k-1。所以,G是k-割宽临界的。 对整数k≥ 1,本文首先刻画了k-割宽图的一个结构,改进和推广了己有结果。 其次,建立了一类k-割宽临界图,其中包含于推论3.4的方法可以构造更多的k-割宽临界图。对一个较大的整数k0≥4, 尽管找到所有的k0-割宽临界图是困难的,然而其中大部分图的结构是有规律可循的。因此,刻画它们的结构特征将是进一步研究的任务。
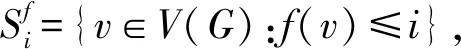
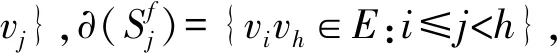
2 主要结果

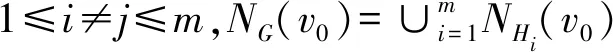

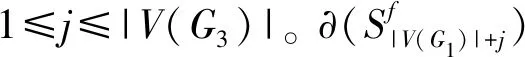
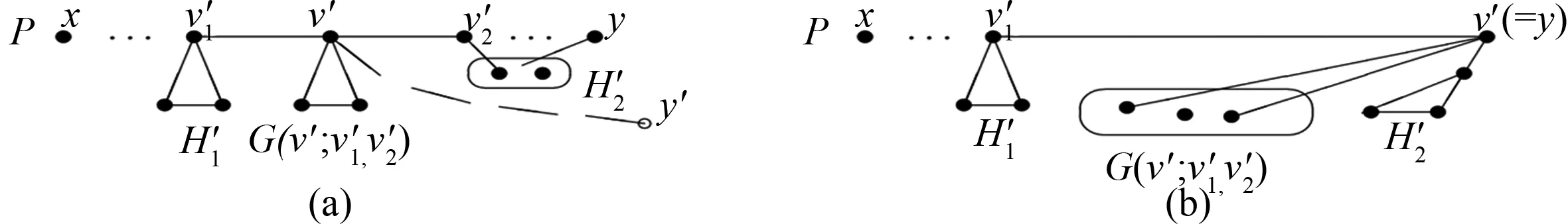


3 应用