聚焦核心素养 突出关键能力——2021年新高考数学Ⅱ卷评析

湖北省襄阳市第一中学 (441000) 叶德凤 王 勇

2021年新高考数学Ⅱ卷落实《课程标准》的理念，稳中求新，聚焦核心素养，突出关键能力的考查，体现了高考数学的科学选拔功能和育人导向作用.试题突出数学本质，重视理性思维，坚持素养导向、能力为重的命题原则，科学把握数学题型的开放性与数学思维的开放性，全面体现了基础性、综合性、应用性和创新性的考查要求.

试卷有利于科学选拔人才，有利于深化课程改革，有利于促进社会公平，对培养考生的创新精神、实践能力，落实“五育”并举，提升考生核心素养有积极的导向作用.

一、对单项选择题的评析

其中第4题、第8题有一定的难度，下面分别解析，供研读.

例1 (第4题)北斗三号全球卫星导航系统是我国航天事业的重要成果.如图1，在卫星导航系统中，地球静止同步轨道卫星的轨道位于地球赤道所在平面，轨道高度为36000km(轨道高度是指卫星到地球表面的最短距离)，把地球看成一个球心为O，半径r为6400km的球，其上点A的纬度是指OA与赤道所在平面所成角的度数，地球表面能直接观测到的一颗地球静止同步轨道卫星的点的纬度的最大值记为α，该卫星信号覆盖的地球表面面积为S=2πr2(1-cosα)(单位km2)，则S占地球表面积的百分比约为( ).

图1

A.26%B.34%C.42%D.50%

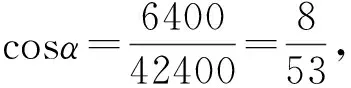
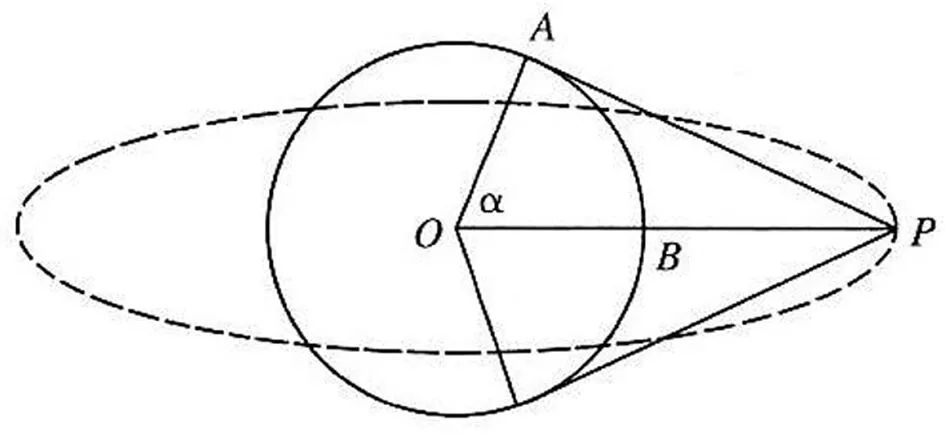
图2

点评：本题以北斗三号全球卫星导航系统为背景，考查解三角形在实际生活中的应用，引导考生关注我国科技进步与发展，增强民族自豪感与自信心.

例2 (第8题)设函数f(x)的定义域为R，且f(x+2)为偶函数，f(2x+1)为奇函数，则( ).

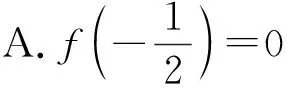
C.f(2)=0 D.f(4)=0

解析：因为f(x+2)为偶函数，所以f(-x+2)=f(x+2)，所以函数f(x)的图象关于直线x=2对称，所以f(x)=f(4-x).因为f(2x+1)为奇函数，所以f(-2x+1)=-f(2x+1)，则f(1)=0，且函数f(x)的图象关于点(1,0)对称，所以f(-1)=-f(3)=-f(1)，故选B.

点评：本题考查函数的奇偶性、对称性及周期性，求函数值等.考查的关键能力是逻辑思维能力、运算求解能力.考查的学科素养是理性思维、数学应用、数学探索.

二、对多项选择题的评析

考查目标第9题考查样本的数字特征第10题考查空间中直线与直线的位置关系第11题考查点与圆的位置关系、直线与圆的位置关系第12题考查对新定义的理解及活用

其中第12题值得认真研读和品味.

例3 (第12题)设正整数n=a0·20+a1·21+a2·22+…+ak-1·2k-1+ak·2k，其中ai∈{0,1}(i=0,1,2,…,k)，记ω(n)=a0+a1+…+ak，则( ).

A.ω(2n)=ω(n) B.ω(2n+3)=ω(n)+1

C.ω(8n+5)=ω(4n+3) D.ω(2n-1)=n

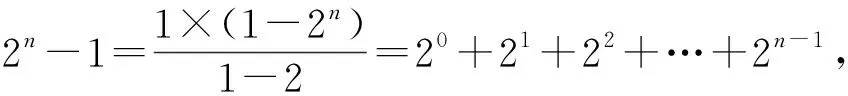
点评：本题是一道信息迁移题，考查考生的阅读理解能力及创新意识.抓住ω(n)表示n的二进制数各位上的数字和是求解问题的关键，对于B选项通过特例法作出判断简化了解题过程.

三、对填空题的评析

考查目标第13题考查双曲线的几何性质第14题考查函数的奇偶性和单调性、函数的导数的应用第15题考查平面向量的模与数量积运算第16题考查导数的几何意义、函数的图象及目标式取值范围的界定等

其中第14题、第16题颇有研讨价值，下面分别详解，供研讨.

例4 (第14题)写出一个同时具有下列性质①②③的函数f(x)=.

①f(x1x2)=f(x1)f(x2)；②当x∈(0,+∞)时，f′(x)>0；③f′(x)是奇函数.

解析：由②和③可知f(x)=x2符合要求，又f(x)=x2满足f(x1x2)=f(x1)f(x2)，即具有性质①，故f(x)=x2满足题意.(本题答案不唯一，符合题意即可)

点评：本题是一道开放性试题，答案不唯一，求解方法多样化，有利于考查考生思维的灵活性和发散性.本题是开放性填空题，是新高考题型改革创新的新动向.

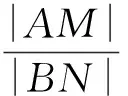
解析：作出函数f(x)=|ex-1|的图象如图3所示，由题意知两条切线的斜率存在且不为零.

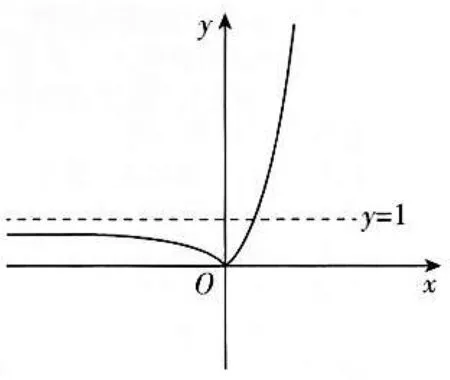
图3

当x∈(-∞,0)时，

f(x)=1-ex，f′(x)=-ex，在点A(x1,f(x1))处的切线斜率k1=f′(x1)=-ex1；当x∈(0,+∞)时，

f(x)=ex-1，f′(x)=ex，在点B(x2,f(x2))处的切线斜率k2=f′(x2)=ex2.因为两条切线互相垂直，所以k1k2=-1，即(-ex1)ex2=-1，即ex1+x2=1，所以x1+x2=0.在点A(x1,1-ex1)处的切线方程为

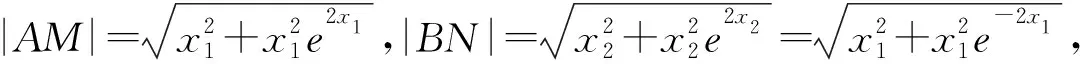
四、对解答题的评析

1.数列题——中规中矩送大礼

本题考查等差数列的通项公式与前n项和公式，考查运算求解能力、推理论证能力，考查数学运算核心素养.第(1)问利用已知条件及等差数列的通项公式和前n项和公式求解出a1和d的值，即可求解；第(2)问在第(1)问的基础上求出等差数列的前n项和Sn，再将Sn>an进行转化，解不等式即可得解.本题与学生平时的训练题极为相似，绝大多数考生当笑纳“大礼”.

2.三角题——平平淡淡考功底

本题考查正弦定理、余弦定理、三角形的面积公式，考查运算求解能力，考查划归与转化思想.第(1)问利用正弦定理求出a,b,c的值，结合余弦定理及三角形的面积公式即可求解；第(2)问根据已知条件得要存在满足条件的正整数a，则角C为钝角，利用余弦定理及三角形的三边关系即可得解.

3.立体几何题——难易适中合情理

本题考查面面垂直的证明及二面角余弦值的求解，考查空间想象能力、运算求解能力.第(1)问由等腰三角形的性质结合勾股定理的逆定理证明线面垂直，再由面面垂直的判定定理即可得证；第(2)问以E为坐标原点建立适当的空间直角坐标系，分别求出平面BQD与平面DQA的一个法向量，利用空间向量的夹角公式即可得解.

4.解析几何题——精打细算求真理

本题考查椭圆方程、椭圆的几何性质、直线与圆、椭圆的位置关系等，考查运算求解能力、推理论证能力、化归与转化思想.第(1)问非常简单，近乎“送分”；第(2)问运算量较大，细节问题要考虑周全，有一定的难度，具有较好的区分和选拔功能.

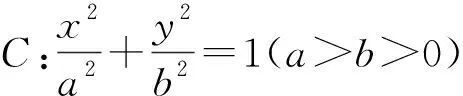
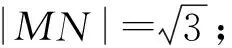
5.概率统计题——想说爱你不容易

本题考查数学期望、利用导数研究函数的单调性与极值、零点存在性定理等，考查阅读理解能力、数据处理能力、推理论证能力，考查的学科素养是理性思维、数学探索.第(1)问比较简单，绝大多数考生志在必得；第(2)问难度较大，考查导数知识的灵活应用；第(3)问在第(2)问的基础上，只有真正领悟了问题的实质方可圆满解答.

例7 (第21题)一种微生物群体可以经过自身繁殖不断生存下来，设一个这种微生物为第0代，经过一次繁殖后为第1代，再经过一次繁殖后为第2代，…，该微生物每代繁殖的个数是相互独立的且有相同的分布列，设X表示1个微生物个体繁殖下一代的个数，P(X=i)=pi>0(i=0,1,2,3).

(1)已知p0=0.4，p1=0.3,p2=0.2,p3=0.1，求E(X)；(2)设p表示该种微生物经过多代繁殖后临近灭绝的概率，p是关于x的方程p0+p1x+p2x2+p3x3=x的一个最小正实根，求证：当E(X)≤1时，p=1，当E(X)>1时，p<1；(3)根据你的理解说明第(2)问结论的实际含义.

解题思路：(1)由数学期望公式即可求解；(2)对方程变形，构造函数，并对其求导(二次求导)，分E(X)≤1和E(X)>1两种情况讨论即可得证；(3)根据第(2)问中的结论结合理性分析即可获得其实际含义.

6.函数与导数题——结构不良添新意

本题考查利用导数研究函数的单调性和极值、函数的零点，考查运算求解能力、推理论证能力.第(1)问多数考生可顺利求解；第(2)问是一道结构不良问题，对考生的逻辑推理、数学抽象、直观想象等素养有较深入的考查，体现了素养导向、能力为重的命题原则.

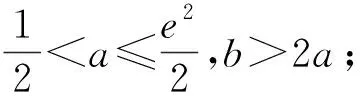
注：如果选择两个条件分别解答，那么按第一个解答计分.

解题思路：(1)f(x)→f′(x)

总之，2021年新高考数学Ⅱ卷试题闪耀着理性思维的光芒，以问题情境设置为载体，考查核心价值和能力素养.试题聚焦学科主干知识，突出学科关键能力，关注社会生活和实践应用，很好地体现了“一核四层四翼”的考查要求，很好地把握了稳定、改革与创新之间的关系，彰显了立德树人价值引领与核心素养育人导向.