基于场协同理论的圆管内插入多孔介质的数值模拟研究
2021-11-18朱江程
曹 颖 杜 辉 江 标 朱江程
(珠海格力电器股份有限公司 珠海 519070)
引言
换热器是应用广泛的换热设备,强化换热器的换热一直是国内外学者的研究热点。研究表明改变换热管的结构对增强换热的效果很明显,国内外学者研究了很多不同结构换热管的换热特性。Shohel Mahmud等[1]采用有限容积法进行数值模拟,得出理想条件下正弦波纹管内压降、速度及传热特性的分布规律。刘伟等[2]证实在圆管内插入金属材料的多孔介质可以强化管内传热。但是对管内插入多孔介质的局部结构对传热、流动热性的研究报道较少。过增元院士[3,4]从速度场和温度场相互配合的角度分析提出了对流换热的场协同原理,场协同原理能够很清晰地显示换热管内部每一点的换热效果。为强化换热管的换热提供了理论指导。因而本文运用FLUENT软件,采用模平均角[5]的计算公式来计算场协同角,以此作为多孔介质换热管的强化传热场协同性的评价标准,分析在圆管内分段插入多孔介质、分层插入多孔介质和插入环状多孔介质的局部换热机理,研究结构对流动及换热性能的影响。
1 计算模型和数值条件
1.1 控制方程
多孔介质换热管管内传热与流动过程受物理守恒定律的支配,即必须要遵循质量守恒定律、动量守恒定律和能量守恒定律。计算流体动力学的控制方程是对这些守恒定律的数学描述,控制方程[6]的通用形式为:

1.2 数值计算模型及边界条件
本文选取的多孔介质换热管管模型如图1所示,具体结构参数如表1所示。

表1 多孔介质模型尺寸

图1 多孔介质填充模型
流体在多孔介质换热管内周期性流动,为了使管内流体充分发展在入口段加长为1 500 mm的圆管,同时为防止尾流段对模拟结果产生影响,在尾部加200 mm的直管段。选择基于压力的隐式稳态求解器,采用非结构化的六面体网格。能量与动量方程的离散格式采用采用QUICK格式,压力与速度耦合方式采用SIMPLEC算法,收敛条件为连续性方程,动量方程以及能量方程的计算残差均小于10-6。以水为工质,采用速度入口和压力出口边界条件。空气的进口温度293 K,出口处的回流温度为293 K,圆管壁面无滑移,采用定壁温350 K加热条件,管壁温度为恒定值350 K,无速度滑移壁面边界条件。不考虑壁面厚度,忽略重力影响。
2 管内分段插入多孔介质的流动与传热特性分析
2.1 多孔介质分段填充方法对管内流动与换热的影响
图2(a)、图2(b)给出了插入不同长度多孔介质和不同长度空隙的管内平均Nu数和摩擦阻力系数与Re数之间的关系曲线。总体所有管型的Nu数都随Re数的增大而增大,摩擦阻力系数都随Re数的增大而减小,从图中1#、4#和5#管很明显地看出,当圆管中按不同距离插入相同长度的多孔介质时,多孔介质间隙越小的Nu数随大,即管内总体插入多孔介质越多Nu数随大,换热效果越好。但是相应的摩擦阻力系数也变大了;从图中1#、2#和3#管可以看出,当固定多孔介质的间隙,分段插入不同长度的多孔介质时,插入多孔介质的长度越长的管子换热效果越好。但是,值得注意的是,无论采用何种分段插入方式,其换热效果均小于全部填充多孔介质。虽然管内全部填充多孔介质时换热最好,但是其摩擦阻力系数也是最大的。

图2 变化曲线
2.2 传热强化综合因子


表2 流体的入口速度和雷诺数

式中:
Nu0和f0—圆管或波纹管内流体的努塞尔数和流体阻力系数。
图3显示了分段插入多孔介质时传热强化综合因子随着Re数的增加呈现逐渐减小的趋势,从图中可以看出,无论以何种方式分段插入多孔介质,其综合换热换热效果均没有全部插入多孔介质时换热好,但是管内全部填充多孔介质大大增加了管内流动阻力,为了既减小阻力又可以强化管内换热,下面采用管内分层插入多孔介质方式,对管内传热与流动进行研究与分析。

图3 综合传热因子
这一结论为工程应用选择管型提供了依据。
3 管内分层插入多孔介质的流动与传热特性分析
3.1 多孔介质孔隙率对管内传热与流动的影响
图4(a)、图4(b)为在圆管内分两层插入多孔介质的传热与流动阻力曲线关系图,从7#、8#和9#管的曲线图中可以看出,当外层均插入孔隙率为0.95的多孔介质,内层分别填满孔隙率为0.8、1、0.9的多孔介质时,当Re<1 500时,内层多孔介质孔隙率越小,其换热越好;当Re<1 500时,内层多孔介质孔隙率越大,换热效果越好。但是管内的摩擦阻力随着内层多孔介质孔隙率的减小而增大。
图4(a)显示了在圆管内分两层插入不同孔隙率的多孔介质的传热强化综合因子变化曲线图。从图中可以看出,无论内外层孔隙率如何变化,只有在管内孔隙率为1,即不填充任何多孔介质的情况下,其综合换热效果最好。下面我们研究管内插入环状多孔介质的填充厚度对管内传热与流动的影响。

图4 分层插入多孔介质时Nu数和f随Re数变化曲线
3.2 传热强化综合因子
图5显示了在圆管内分两层插入不同孔隙率的多孔介质的传热强化综合因子变化曲线图。从图中可以看出,无论内外层孔隙率如何变化,只有在管内孔隙率为1,即不填充任何多孔介质的情况下,其综合换热效果最好。下面我们研究管内插入环状多孔介质的填充厚度对管内传热与流动的影响。
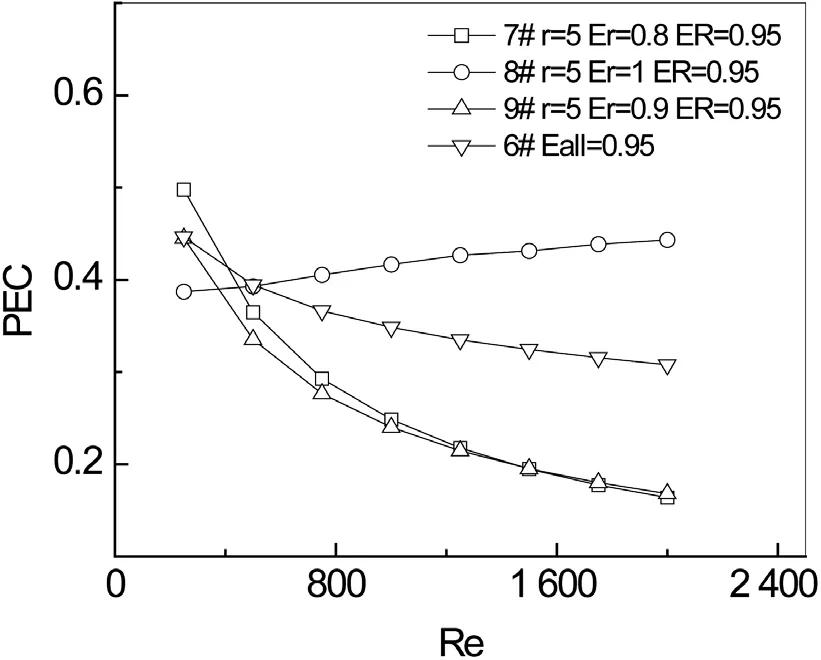
图5 综合传热因子
4 管内插入环状多孔介质的流动与传热特性分析
4.1 环状多孔介质填充厚度对管内换热与摩擦阻力的影响
图6(a)、图6(b)为在圆管内插入环状多孔介质的传热与流动阻力曲线关系图,8#、11#、12#为分别在管内插入厚度为5 mm、7 mm和3 mm的多孔介质。从图中可以看出,管内插入多孔介质的厚度越大,其换热越好,但是摩擦阻力越大。

图6 管内插入环状多孔介质时Nu数和f随Re数变化曲线
4.2 环状多孔介质填充厚度对管内换热与摩擦阻力的影响
图7为在圆管内插入环状多孔介质的传热强化综合因子变化曲线图。可知,当Re<1 700时,厚度为7 mm的环状多孔介质综合换热效果好;当Re>1 700时,厚度为5 mm的多孔介质综合换热效果好。得出在所研究的条件下,5#管的换热效果最好。这为换热管的选型提供了理论依据。
5 场协同理论分析管内插入多孔介质的换热机理
5.1 协同角沿轴向位置变化
为了全面考察管内插入多孔介质的圆管内温度场和速度场协同效果,对协同角沿轴线的分布情况进行了分析。图8为Re=1 000时各种不同管型平均协同角随截面轴向位置的变化曲线。从图中可以看出,分段插入多孔介质时,每逢流体进入多孔介质时,由于多孔介质内的空隙,是流体分流,协同角在多孔介质区域增加,导致其内温度场和速度场的协同效果变好,流体在多孔介质区域换热效果较好。当管内分层插入多孔介质时,协同角的变化区域平稳,但是均值较大。但仅仅是插入环状的多孔介质时,其管内协同角存在跳跃,均值相对来说较小,协同效果较好。
5.2 协同角沿径向位置变化
为了准确的分析不同多孔介质的插入方法对管内部协同角沿径向的分布特点,同样选择上述四种管型为研究对象,提取Re=1 000时,x=1.725 m时圆管轴向中心处对应的轴截面的数据分析计算。图9中横坐标表示无量纲的径向位置,纵坐标表示微元面的平均协同角。从图中7#、11#管可以看出,分层插入多孔介质的圆管,内层孔隙率小或者是没有插入多孔介质,流体往管子中心聚拢,扰乱了流体流动方向,在管子中心处形成较大的漩涡,因而越靠近管子中心区域协同角越小,换热效果越好。但是靠近壁面处的的换热相对差些。从图中4#、6#管可以看出,管内协同角区域跳动,但是平均值相对较低。
6 结论
通过大量的数值计算,获得了不同结构的波纹管湍流流动与的特征与规律,并利用场协同理论,分析了流场和温度场的协同特征,得出以下结论:
1)管内分段插入多孔介质时,多孔介质区域轴线中心处形成漩涡;所有管型的Nu数都随Re数的增大而增大,摩擦阻力系数都随Re数的增大而减小。插入相同长度的多孔介质,间隙越小Nu数越大。间隙相同时,插入多孔介质的长度越长换热越好;但综合换热效果管内填充满多孔介质时要好于分段插入多孔介质。
2)管内分层插入多孔介质时,填充大孔隙率的外层温度梯度较小,填充小孔隙率的内层温度梯度变化较大;当Re<1 500时,内层多孔介质孔隙率越小,其换热越好;当Re≥1 500时,内层多孔介质孔隙率越大,换热效果越好;在所研究的范围内,分层插入多孔介质时,当管内层插入的孔隙率为1,即内层不插入任何多孔介质时,换热效果最好。
3)管内插入环状多孔介质时,管内温度梯度相对前两个均小,除了入口段处温度梯度较大外,其余部分的温度等值线均趋于沿轴向方向,环状多孔介质的插入均匀化了管内温度分布;管内插入多孔介质的厚度越大,其换热越好,但是摩擦阻力越大;当Re<1 700时,厚度为7 mm的环状多孔介质综合换热效果好;当Re>1 700时,厚度为5 mm的多孔介质综合换热效果好。综合所研究的几种管型5#管的换热效果最好。
