基于改进布谷鸟搜索算法的多传感器调度方法*

魏文凤，刘昌云，田桂林，岳韶华

（1.空军工程大学防空反导学院，西安 710051；2.空军工程大学研究生院，西安 710051）

0 引言

20 世纪以来，随着通信技术的飞跃发展，现代战争正在逐步信息化，多传感器数据融合技在获取探测信息和数据采集方面有着广泛的应用。为了进行最优数据获取，对有限的传感器资源进行合理的分配利用是非常重要的。多传感器资源调度是依据一定的优化准则，在确定的时间区间内，为传感器网络中的各传感器资源安排跟踪探测任务，以满足对多目标的跟踪要求，从而达到某项或某些指标的综合最优［1-2］。传感器调度可以改善多传感器系统的系统性能，提高其运行速率，因此，合理的传感器调度是机动目标跟踪领域中的研究热点。

本文是在多传感器多目标跟踪任务下进行研究，在该领域多数研究有在给定传感器序列下对所有目标跟踪精度的计算方法，如Chakravarty［3］提出的粒子滤波法；Preeti A［4］提出了决策树方法；乔成霖［5］等提出建立基于部分马尔可夫决策过程（POMDP）的目标跟踪与辐射控制模型，以随机分布粒子计算新生目标检测概率，以后验克拉美-罗下界（PCRLB）预测长时跟踪精度，利用基于贪婪搜索的分支定界算法求解最优调度序列；李建平［6］用跟踪目标的重要程度之和作为目标函数，建立了0-1规划的数学模型，并利用割平面方法求解得出最优调度策略。除此之外，近年来新兴的智能算法也开始被用于传感器调度的问题，如任俊亮［7］、刘建业［8］以及胡崇海［9］等分别采用了自适应粒子群算法、遗传模拟退火算法，以及动态连续蚁群算法来解决不同背景下的传感器调度问题。

多传感器多目标跟踪任务下的传感器是一个复杂的组合优化问题，目前，用来求解大规模优化问题时常用的方法有群智能算法，比如，遗传算法、模拟退火算法、蚁群算法等。这些算法都在可允许的时间范围内得出近似最优解。而布谷鸟算法［10-11］（Cuckoo Search，CS）是一种模仿布谷鸟行为的仿生算法，具有算法流程简单、计算速度快、参数少等特点，因而得到了广泛应用。但是布谷鸟搜索算法依赖随机步长，故存在收敛速度慢、精度较低的问题，且比较适用于求解连续型优化问题，而多传感器调度属于离散型的组合优化问题。因而，为提高多传感器调度算法的收敛速度和精度，在CS 算法过程中引入差分进化算法，提高布谷鸟算法种群多样性，以提高其收敛时间和精度。仿真结果表明，利用DE-CS 算法求解目标跟踪背景下的多传感器调度模型，具有较快的收敛速度和较高的精度。

1 多传感器多目标跟踪下的传感器调度模型

在多传感器多跟踪目标任务背景下，传感器调度需要综合考虑多方面的指标要求。首先，从任务完成方面来讲，要求尽可能提高跟踪任务的跟踪精度，此项指标可以从跟踪模型中传感器滤波协方差、传感器滤波估计状态与目标实际状态之间的位置均方误差反映得出；其次，从系统角度来讲，要求多传感器系统尽可能多地完成任务；第三，由于传感器节点的可利用资源是有限的，如何最有效地利用资源，尽可能延长传感器的生命周期，也是传感器调度过程中全都需要考虑的问题。

1.1 决策变量

1.2 调度指标及目标函数

1）跟踪精度Cα

针对单目标t，pt（k|k）是在时刻k 对目标状态的估计误差协方差矩阵，如果传感器调度结束的时刻为k，根据目标跟踪模型计算得到pt（k|k），pt（k|k）也就是在该调度序列下对跟踪任务t 的跟踪误差矩阵。跟踪精度需要综合考虑所有的目标跟踪精度，李国辉［12］等提出，利用pt（k|k）的迹（Trace）计算任务t 的跟踪精度dt，如式（1）。

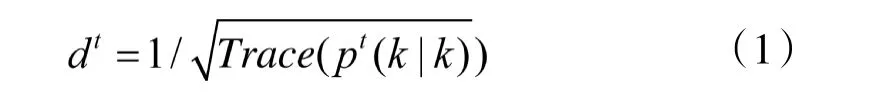
设M 为要跟踪的目标总数量，Cα是所有跟踪目标的精度均值，如式（2）。

2）任务完成率指标Cβ

在多目标跟踪场景下，有限的传感器资源可能无法满足所有目标的跟踪需求，这就需要区分目标的重要程度，以便对重点目标优先跟踪。也就是说，每一个观测目标都有各自的优先级，目标的优先级取决于目标的类型、速度、飞行距离、飞行航向角以及威胁程度等因素，每个目标的优先级是不同的。因为传感器跟踪观测的能力有限，所以在调度时为了能够更有效地完成任务，具有较高优先级的观测目标会比相对较低的观测目标有更大概率被合适的传感器资源跟踪。故本指标除了能够反应目标被跟踪的数量，也可以反映出在本问题中各目标的优先级。

设目标t 的优先级为pt，Cβ可以用已完成跟踪目标的优先级之和与所有跟踪目标的优先级之和来计算得出，如式（3）。

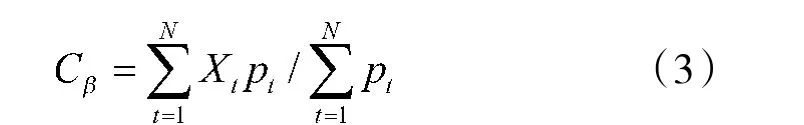
其中，Xt是二进制变量，表示任务t 是否被调度完成，N 是传感器总数量。

3）传感器资源消耗Cμ

传感器资源消耗是指传感器对目标进行探测时消耗的能量，传感器的能量是有限的，要在传感器资源范围内最大程度地进行探测。在此定义传感器资源能耗为Cμ，计算方法参考文献［13］，因为本文设定任务约束（由1.3 中提出），且本文目标函数计算最大值，故改进后计算方法如式（4）。

1.3 约束条件

本文所研究的传感器调度问题在几个方面存在约束：

1）观测时间约束

2 基于差分进化的改进布谷鸟算法

布谷鸟算法是Xin-she Yang 和Suash Deb 提出的一种模仿布谷鸟“巢寄生”行为的仿生算法，该算法流程简单、计算速度快，参数少。布谷鸟搜索算法近些年来得到颇多关注［10-11］，因为它不仅能够在本地搜索，还可以通过Levy 飞行来全球游走，从而进行全球搜索，故而收敛达到全局最优。

2.1 标准布谷鸟搜索算法

2.1.1 Levy 飞行

Levy 飞行是一种流行的随机游走，通过该随机游走可以定义动物或者昆虫在食物搜索空间内的运动。在Levy 飞行中，步长是由具有一定概率分布的分布步长定义的，即重尾概率分布，步长的方向是各向同性且随机的。布谷鸟算法在考虑基于Levy 飞行的随机游走时的效果比在单纯随机游走时更好。在二维平面里模拟Levy 飞行，如图1所示。

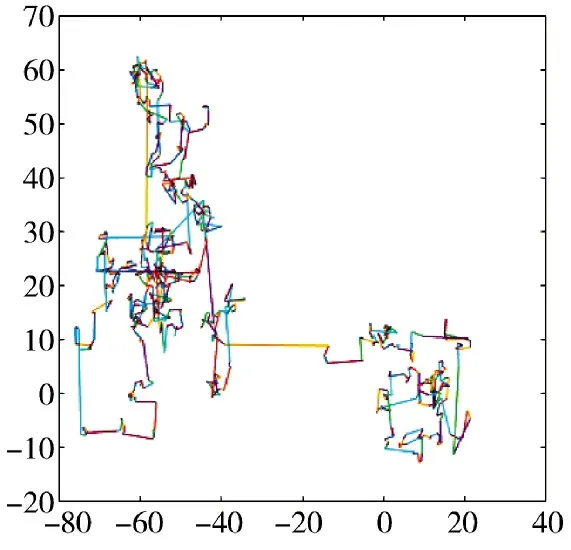
图1 Levy 飞行模拟图

2.1.2 布谷鸟算法的前提

布谷鸟算法以下列3 种假设为前提：

1）每只布谷鸟每次只孵化一个蛋，然后将它放在随机选择的巢中；

2）具有较高品质的巢被视为最佳孵化巢穴，并将延续到下一代；

3）可选用的宿主鸟巢数量是一定的，而布谷鸟的卵有可能被宿主发现而导致孵化失败。

基于以上前提，鸟巢位置更新公式为：

2.2 布谷鸟搜索算法的改进

标准的布谷鸟搜索算法依赖随机步长，故有收敛速度慢的现象，多位学者对该算法利用不同方法进行改进［14-16］。本文借鉴差分进化算法对CS 算法进行改进，以提高其收敛速度和精度，并将其离散化，从而适合解决NP-hard 问题。

差分进化算法［17］是基于种群差异、优胜劣汰的进化算法。该算法通过反复迭代，保留那些适合环境的个体，淘汰适应性弱的个体，是一种被广泛应用的全局优化算法。在标准的布谷鸟搜索算法中，是初始化种群后的鸟巢位置，对进行差分进化操作，此操作后的鸟巢个体可以部分甚至全部继承父辈优秀基因，从而使其像种群中的最优位置迅速靠拢。差分进化之后再回到标准CS 算法，利用Levy飞行对位置进行更行，从而增加了种群多样性，避免陷入局部最优，提高了收敛速度和精度。

具体操作为：

1）变异。变异操作是差分进化算法的关键，此操作可以获得多个个体的遗传信息。根据下式获得变异个体：

改进的布谷鸟搜索算法，称为DE-CS 算法，其具体步骤如下：

步骤1：初始化种群，设置初始参数，随机产生N 个鸟巢的位置。

步骤2：设置终止条件，判断是否有无鸟巢位置满足该条件，若停止，输出最优值，否则，继续步骤3。

步骤3：对初始化鸟巢进行评估并保留较好的位置，按照式（9）通过Levy 飞行随机搜索下一代鸟巢的位置。

步骤4：按照发现概率Pa对鸟巢进行丢弃操作。

步骤5：根据式（11）～ 式（13）进行差分进化操作，并根据式（5）计算目标函数值。然后比较新的鸟巢和之前鸟巢的适应值，保留较优的一个。

步骤6：重复进行步骤3～ 步骤5，判断是否满足终止条件，若满足，则输出最优值；否则，继续进行搜索鸟巢的操作。

3 基于DE-CS 算法的传感器调度仿真流程

根据DE-CS 算法进行传感器调度的仿真流程如图2 所示。

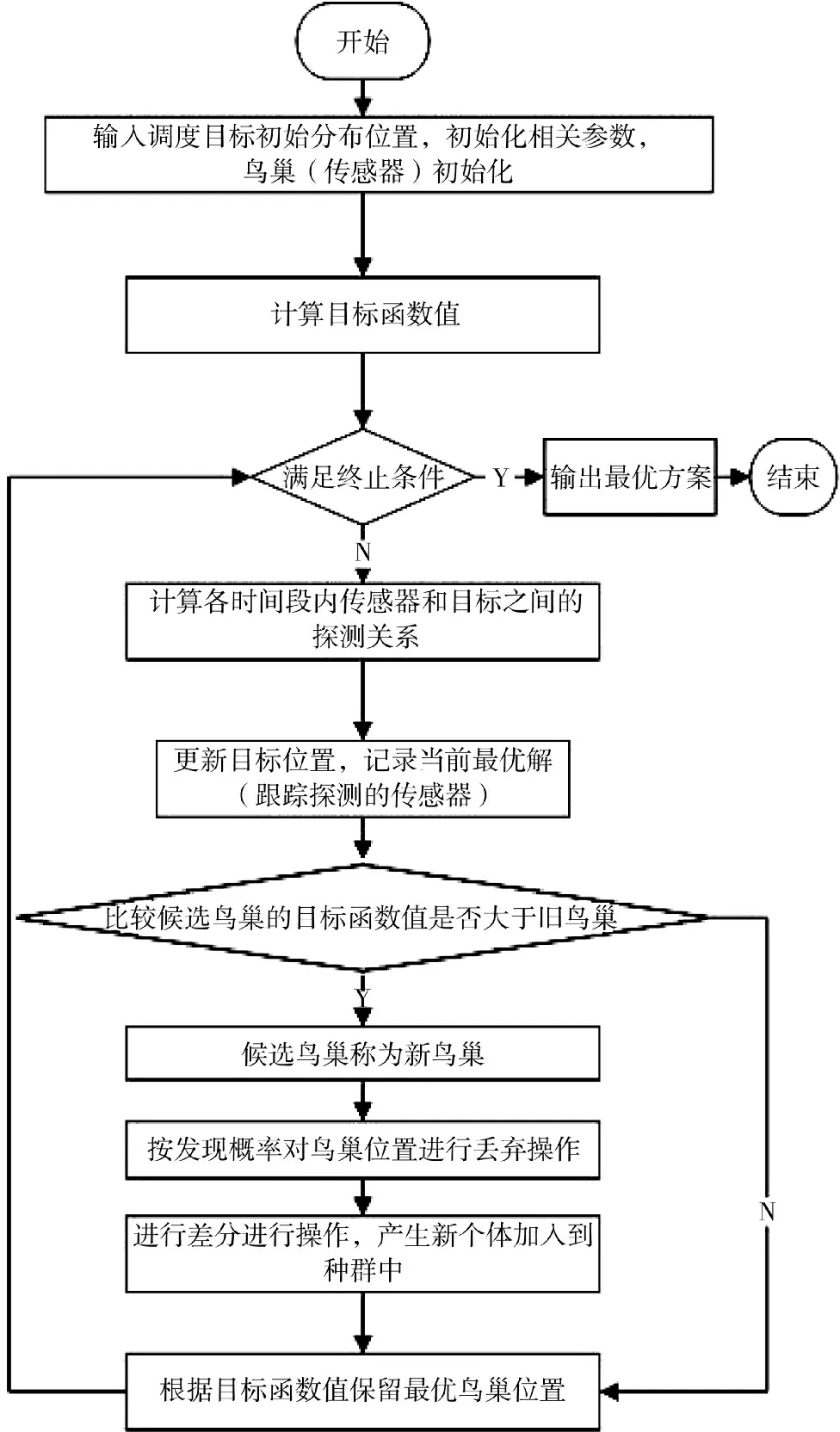
图2 基于DE-CS 算法的多传感器调度仿真流程图

4 仿真分析

4.1 仿真条件

假设作战区域是范围为1 000 km×1 000 km 的一块正方形区域，其坐标范围为从（0，0）至（1 000，1 000），该区域内设置5 个探测传感器。假设在一段时间0 s～1 000 s 内，该区域会出现5 个敌对来袭目标，其观测优先度根据其型号信息可得。为简化运算，这些目标均作直线运动，但其初始位置和方向都是不一样的。其运动轨迹如下页图3 所示。

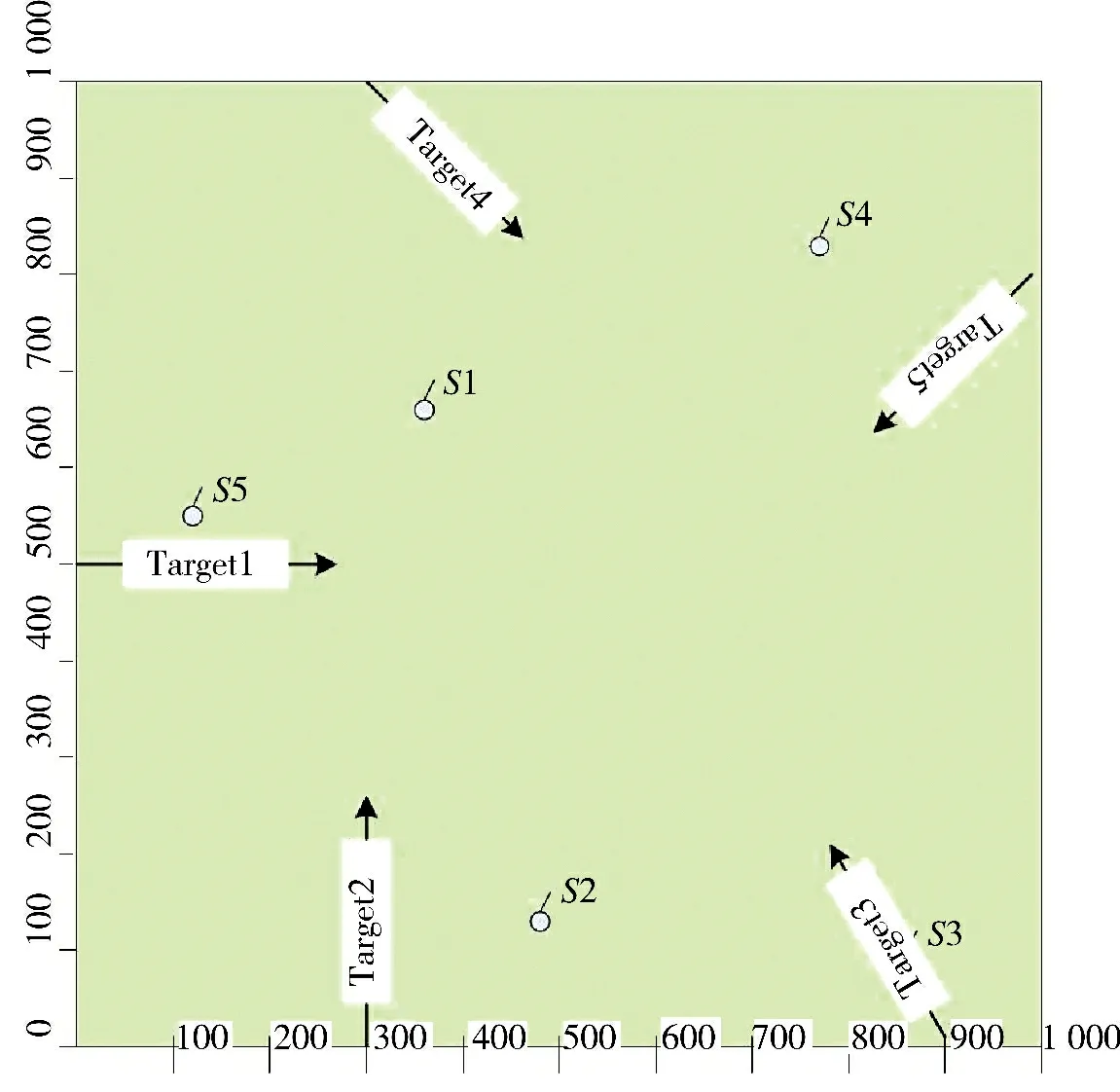
图3 来袭目标运动轨迹

仿真实验中假定的传感器和目标的信息分别如表1～表2 所示。

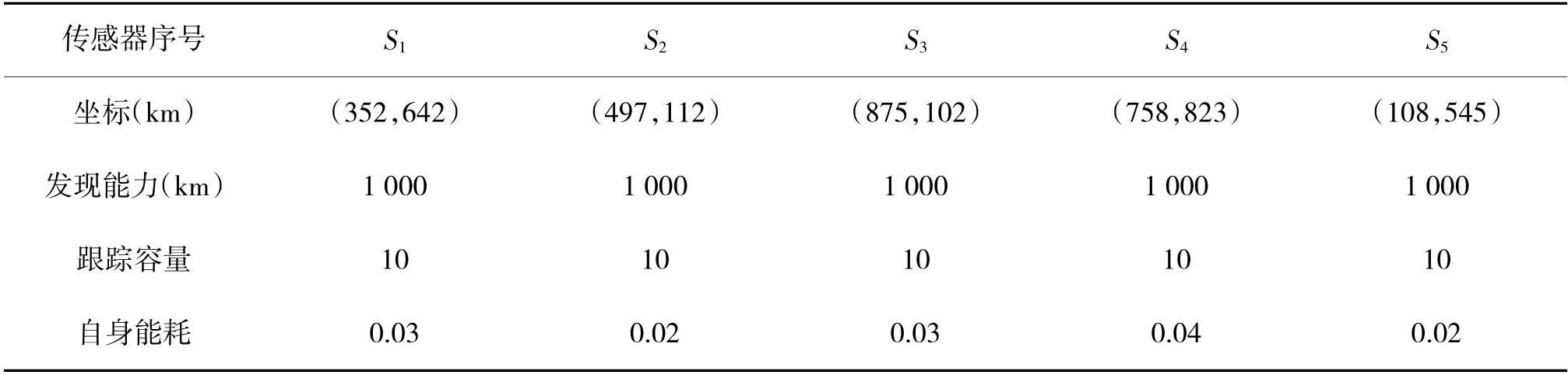
表1 传感器信息

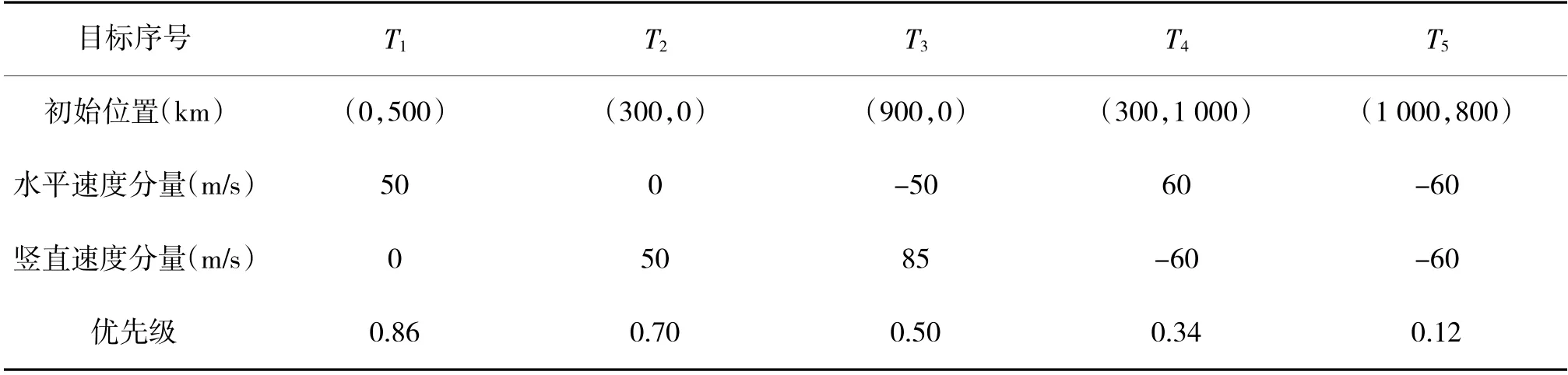
表2 目标信息

将一次调度周期按照时间划分的任务分解方法分成10 个片段，最小观测时间为20 s：［0，98］，［98，182］，［182，201］，［201，350］，［350，405］，［405，531］，［531，550］，［550，720］，［720，840］，［840，1 000］。假设各传感器在可探测时间内对任意目标均可进行探测，则传感器与目标之间一共有5×5×10=250 个可探测关系。调度目的就是在这段时间内将这些目标分配给传感器进行探测跟踪。

4.2 仿真结果与分析

设定布谷鸟搜索算法参数：最大迭代次数为100，发现概率Pa为0.25，交叉概率Pc为0.6。按照本文改进的布谷鸟算法，编制程序，进行仿真。传感器调度结果如图4 所示。

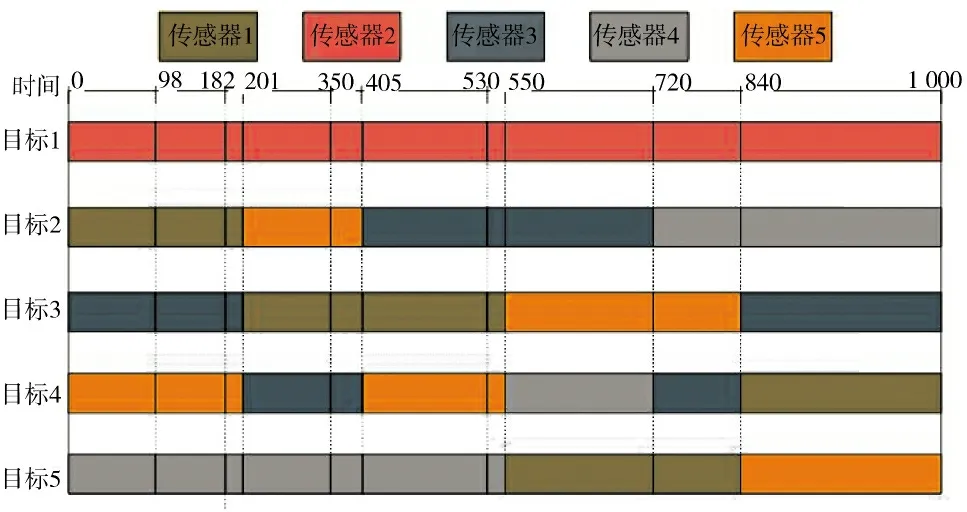
图4 传感器-目标调度结果

为了验证改进后的布谷鸟搜索算法是否具有有效性，将DE-CS 算法与CS 算法分别从性能、收敛敛速度收敛性和算法时间4 个方面进行仿真分析。

4.2.1 性能分析

在参数γα=0.3、γβ=0.5、γμ=0.2，迭代次数为100的条件下，分别对两种算法做10 组实验，实验结果如下页表3 所示。

由表3 中可得：采用DE-CS 算法所求得的最优适应度值高于基础CS 算法所求得的最优适应度值，计算得到DE-CS 算法平均值为0.640 4，CS 算法为0.637 1。这是因为DE-CS 算法在差分进化操作之后能获得更多遗传信息，生成新的个体，在迭代中能够增加种群的多样性，从而避免陷入局部最优，因此，其具有更好的寻优能力，更高的求解性能。

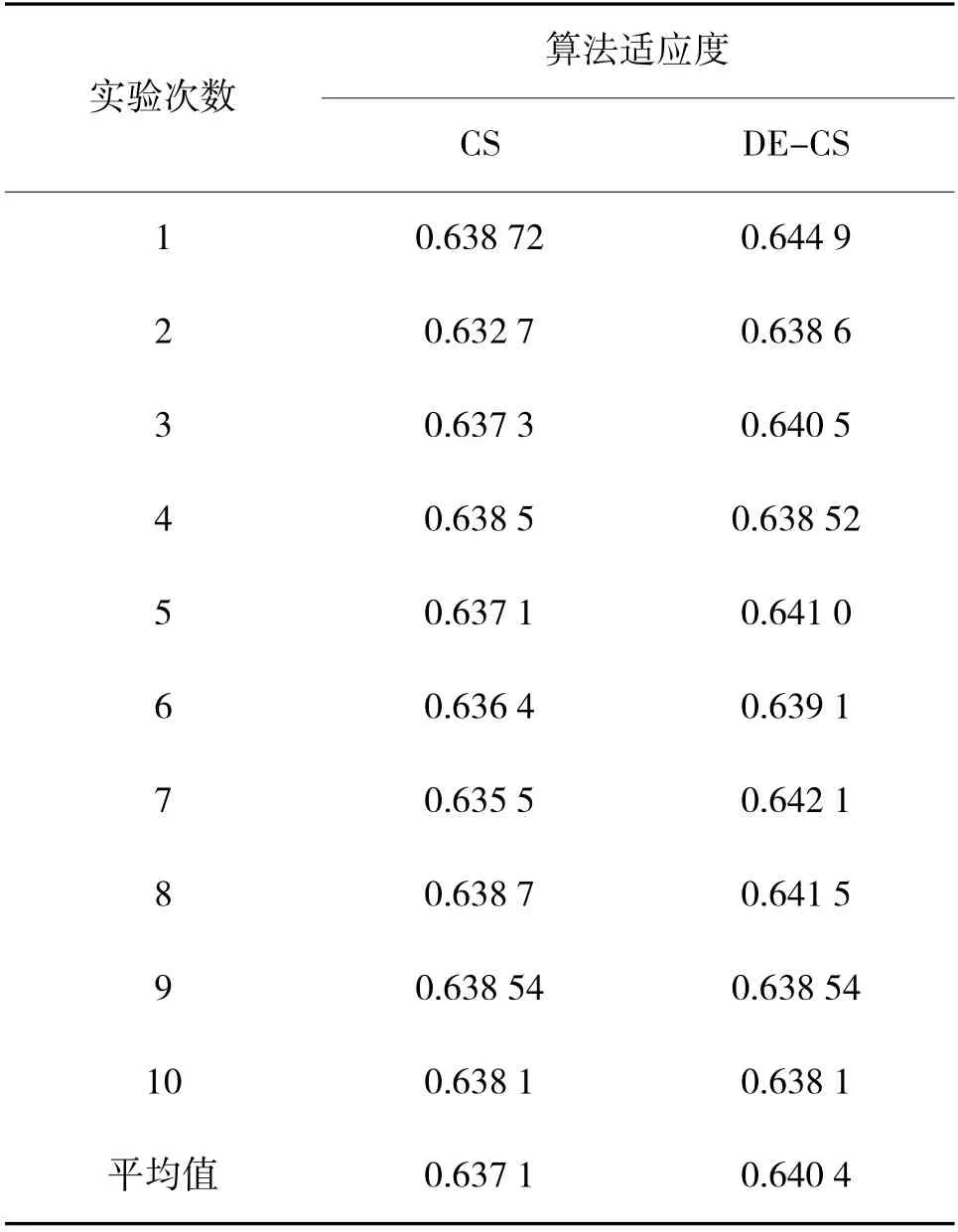
表3 算法最优适应度比较

4.2.2 收敛速度

分别设置迭代次数为10 次、20 次、50 次、100 次记录达到最优时迭代次数。

1）迭代次数为10 次

迭代次数为10 次的CS 算法与DE-CS 算法仿真结果如图5 所示。

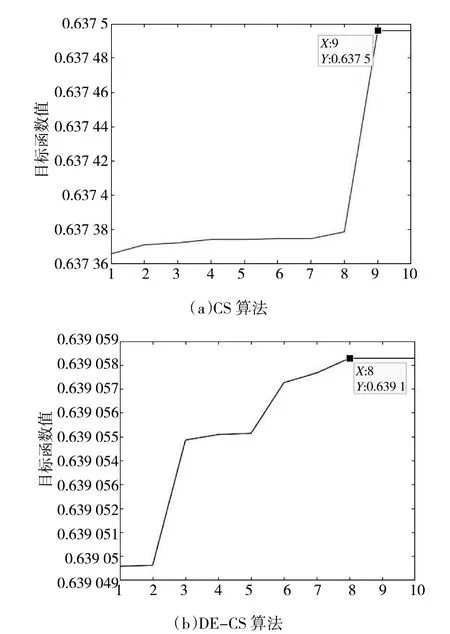
图5 迭代次数10 次对比

2）迭代次数为20 次

迭代次数为20 次的CS 算法与DE-CS 算法仿真结果如图6 所示。

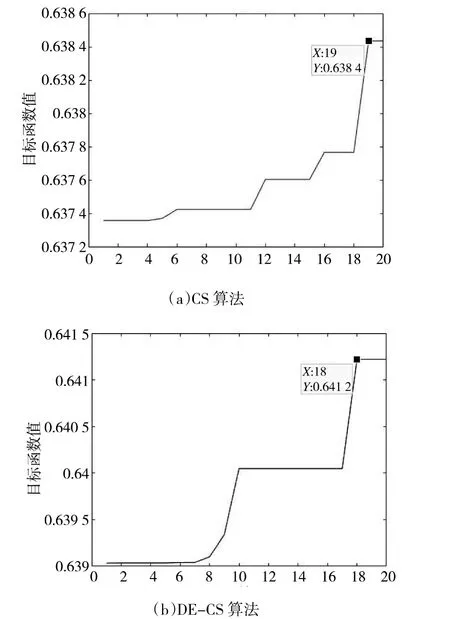
图6 迭代次数20 次对比

3）迭代次数为50 次

迭代次数为50 次的CS 算法与DE-CS 算法仿真结果如下页图7 所示。

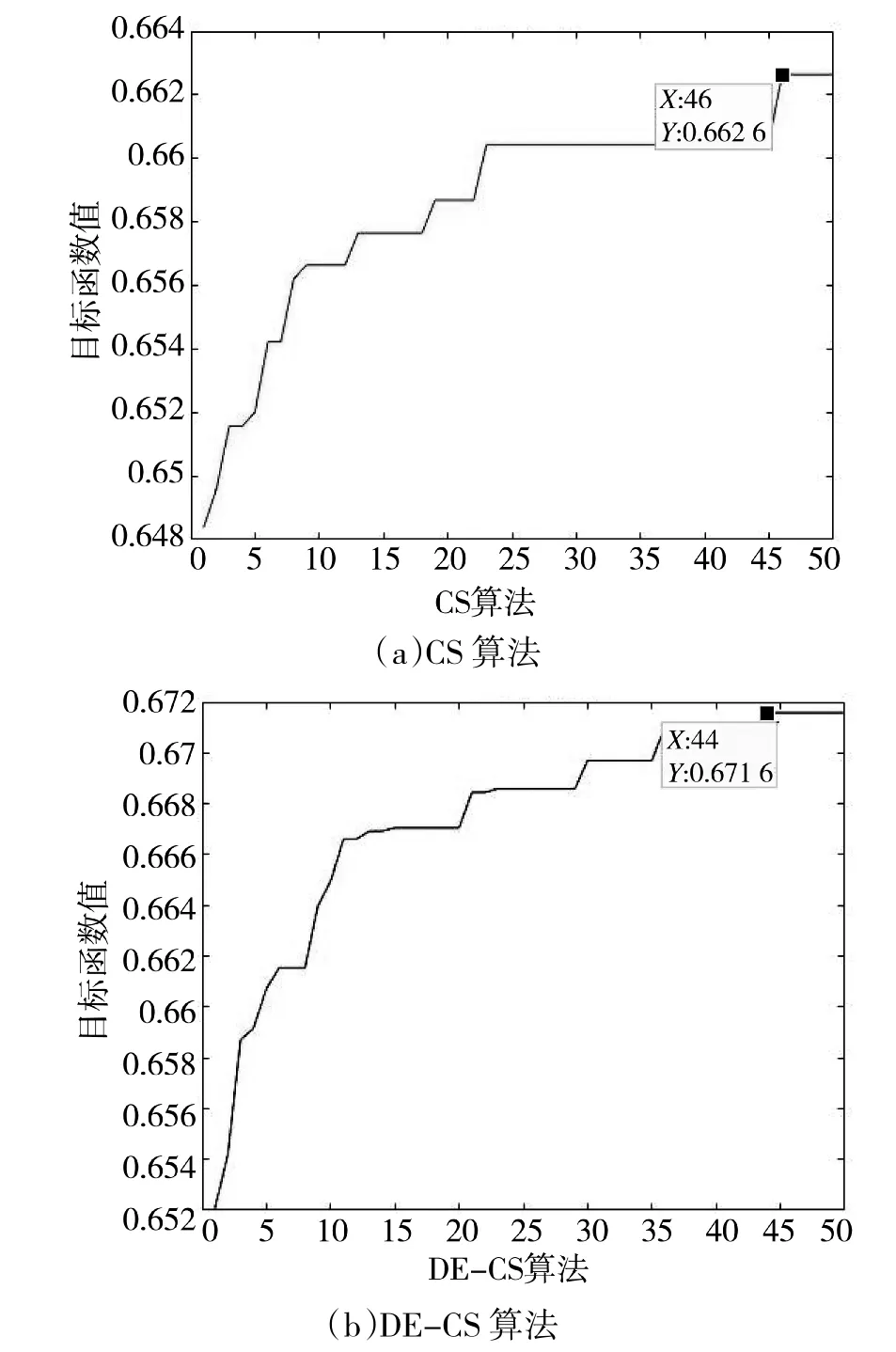
图7 迭代次数50 次对比

4）迭代次数为100 次

迭代次数为100 次的CS 算法与DE-CS 算法仿真结果如图8 所示。

在图5～图8 四组仿真实验图中，横坐标表示迭代次数，纵坐标为目标函数值，标注的点为达到收敛时的迭代次数以及目标函数值，其中，每组实验的（b）为不同迭代次数下DE-CS 算法的仿真结果，（a）为不同迭代次数下标准布谷鸟算法的仿真结果。从4 组仿真结果可得：在相同的条件下（如设置迭代次数为100 次时，DE-CS 算法在第81 次迭代时达到收敛，目标函数值为0.698；基础CS 算法在第91 次迭代时达到收敛，目标函数值为0.681 9），改进后的CS 算法相比于CS 算法除了有更高的适应度值外，且能更快地收敛到最优。

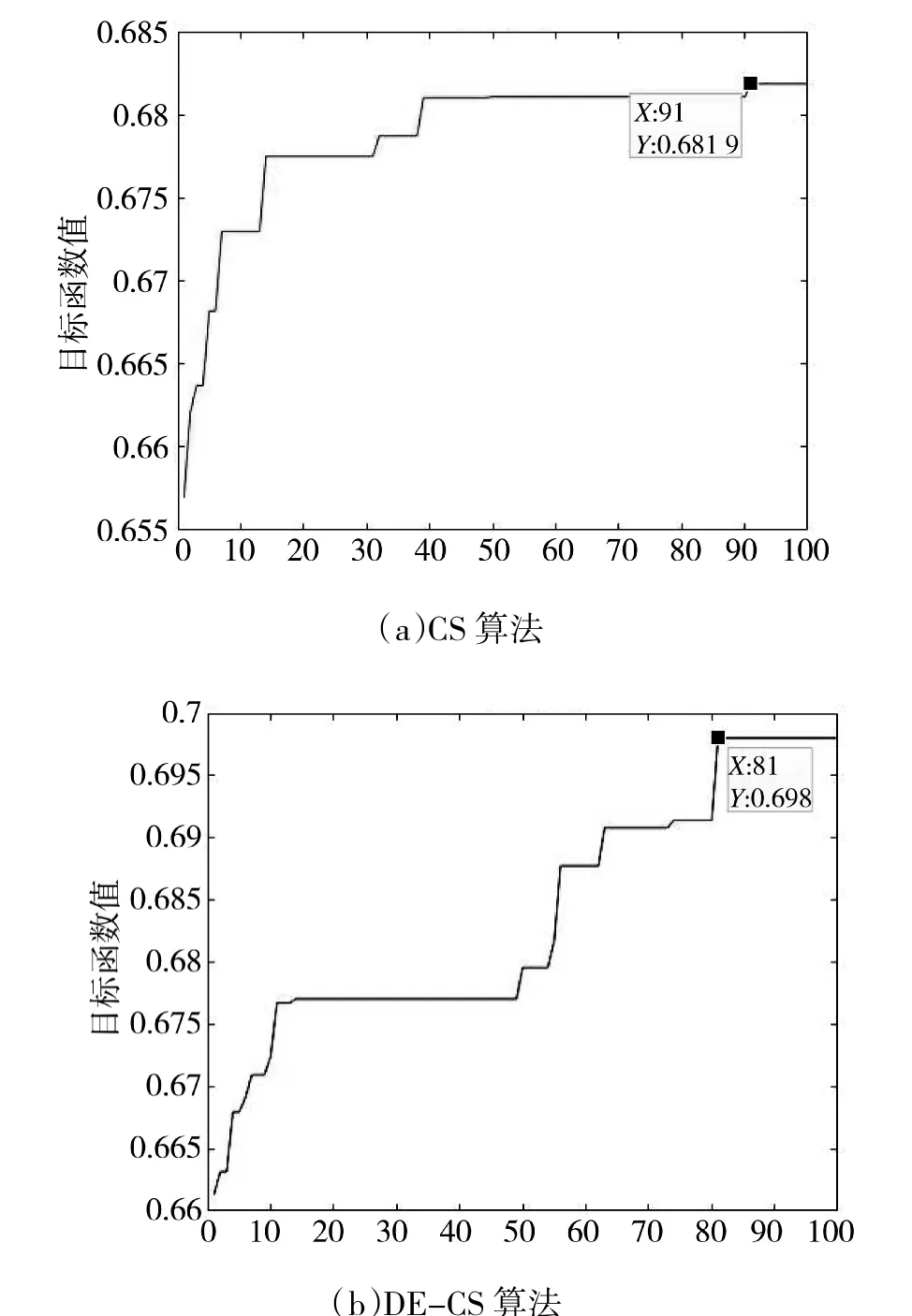
图8 迭代次数100 次对比

4.2.3 收敛性

图9～图10 分别为DE-CS 算法和CS 算法的收敛性曲线，两图相比除了可以看出改进后的DE-CS 算法的最佳适应度函数值高于CS 算法外，收敛性也更好。

图9 DE-CS 算法收敛图

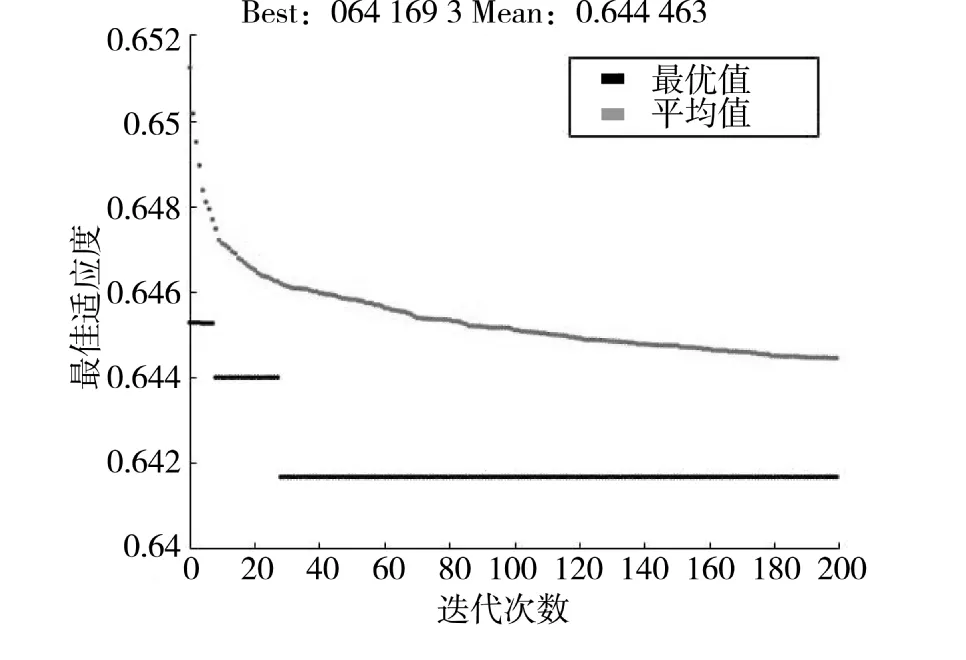
图10 CS 算法收敛图

4.2.4 算法时间

DE-CS 算法和CS 算法在迭代50 次的条件下分别进行10 次实验，平均耗时情况如表4 所示。

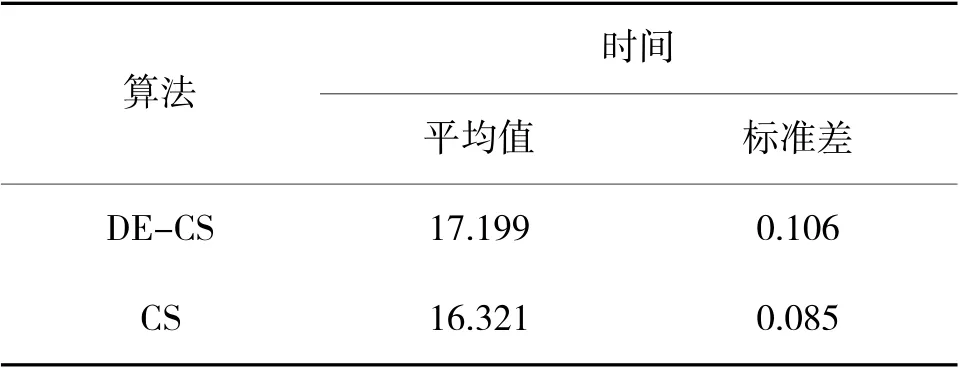
表4 算法时间性能对比

从表4 中可知：DE-CS 算法所耗时长略高于改进之前。两种算法的耗时差距体现在解空间的更新上，因为DE-CS 算法添加了交叉、变异操作，但是这些计算采用并行计算，所以两种算法的时间性能相差在可接受范围内。

综上所述，从算法性能、收敛速度、收敛性方面进行对比，在相同的实验条件下，DE-CS 算法比CS算法有着更好的性能。

5 结论

传感器调度问题是传感器网络管理中的一个重要研究方向，本文针对战场环境下多传感器资源调度问题的特点，建立了基于跟踪精度、目标优先级以及传感器资源消耗率为指标的多传感器调度模型，针对该问题进行任务分解，根据调度周期进行分割，构建目标- 时间- 传感器的模型求解流程，并将改进的CS 算法用于求解该模型，给出了仿真流程以及仿真实例，验证了本文提出的改进算法适用于多传感器多目标的调度问题。仿真实验表明，改进后的布谷鸟算法具有更快的收敛速度、更高的求解性能，对于多传感器多目标的调度问题求解具有更高的有效性。