受电弓混合建模与弓网耦合振动分析

周 群，杨 俭，宋瑞刚，袁天辰

(上海工程技术大学城市轨道交通学院，上海 201620)

1 引言

铁路车辆速度不断提高，受电弓与接触网关系的问题日益突出。接触网试验复杂艰巨，想要保证设计出的弓网系统在列车高速行驶时有良好的运行状态，就要从受电弓入手，分析研究受电弓参数对接触力的影响。当下国内应用的受电弓主要通过从国外引进整弓或零部件再加工，参数缺失，严重影响我国受电弓研发和列车提速的进程[1]。

传统对受电弓的研究多经过确定几何参数和几何运动关系，进而通过复杂物理模型和复杂的公式推导建立运动微分方程[2-3]。此类方法所需参数极多，对于根据特定弓型专门设计的相应的计算方式，当受电弓的类型改变时，应用有所不便。文献[4]针对高速受电弓的力学特点，同时考虑了受电弓的滑板、支架的平面运动以及弓头滑板条的俯仰运动。此类模型比线性模型更加合理全面，但是过于复杂，仿真计算就会困难。付秀通应用有限元方法可以将受电弓系统当做空间系统进行计算[5]。然而，受电弓与接触网的作用主要体现在垂直方向，并且考虑有限元不太适用于大型复杂结构的动态分析。

杨岗等人建立的弓网耦合模型，均是以受电弓线性模型为基础[6]。崔营波建立的弓网非线性模型，利用弓头与上臂杆之间弹簧的弹性系数和阻尼系数的变化模拟弓头的柔性[7]，比线性模型更能反应实际运动情况。但其采用弹簧的弹性系数与受电弓弓头位移的乘积表示弓网间的接触压力，并未将实际接触网结构参数纳入接触网模型构造的考虑中。

M. Tur提到接触导线不平顺的概念，研究了接触导线的不平顺性对弓网受流质量的影响[8]。本文将触网不平顺导致的受电弓弓头垂直方向的振动，即弓头的柔性引入以完善受电弓模型，并考虑到空气抬升力[9]、车体振动的环境影响，针对弓网垂向耦合振动过程，采用基于受电弓等效参数识别的非线性实验建模方法，进行了弓网振动分析。

2 受电弓的混合建模

2.1 受电弓非线性特征分析

将受电弓简单等效为二元归算质量块进行参数的等效。受电弓力学模型主要包括两个部分，如图1所示，由弓头、框架两质量块和其间的刚度阻尼构成。

图1 受电弓结构和二质量块模型图

质量块M1、K1、C1分别为弓头的等效质量以及弓头与框架间的刚度、阻尼；M2、K2、C2分别为框架的等效质量以及框架与基座间的刚度、阻尼；F0为受电弓本身受到的静态抬升力。

弓头与接触导线直接接触，接触网的不平顺将直接作用于弓头，导致弓头呈现非线性。考虑用弓头参数的振动模拟弓头的柔性。参数振动是由外部激励产生的，激励通过系统中参数的周期性变化来实现，这与施加到系统的外力不同[7]。建立的包含非线性平方项的受电弓微分方程组如下

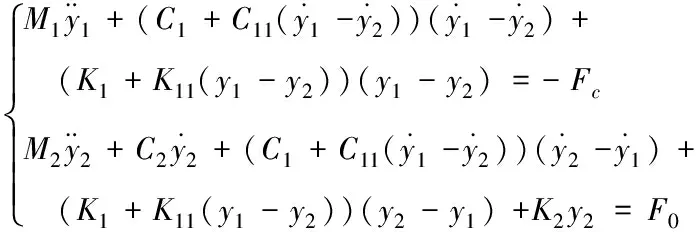
(1)

2.2 线性部分等效参数的测定

2.2.1 框架等效刚度

对于框架，如果严格满足静压力要求，框架的归算刚度应为零[10]。但若联系到工程实际，这么等效显然不满足实际情况，也会影响其它参数的等效结果。

框架在不同升弓高度处对应不同的等效参数值[11]。按我国电气化铁路标准规定，受电弓的工作高度范围是0.4 m-1.9 m，最重要的工作区段是1.5 m[12]。所以，试验利用激光测距仪和测力计采集受电弓1.30 m-1.65 m高度的位移、拉力数据对。拉测试验现场如图2所示。

图2 刚度测试现场图

由于受电弓正常工作时，接触线仅在几厘米的高度范围内变化，因此可将带有固有非线性属性的框架在此一定高度上做线性化处理，用一次线性方程拟合。为保证试验结果可靠，进行多组试验，取其中一组数据拟合结果如图3所示。

图3 实验数据拟合结果图

图中对应的曲线表示对框架横杆施加的拉力方向为自上向下拉测得的位移-力数据对与拟合图像。

测量结果表明，框架刚度存在弱非线性，可在1.30 m-1.65 m工作范围内近似为线性。拟合刚度结果如图中标示，故框架刚度为90 N/m。

2.2.2 框架等效质量与等效阻尼

采用自由振动周期法测框架质量和阻尼。为避免弓头影响，可将弓头直接拆下。考虑到工程实际和实验室条件，引入两个刚度各为150 N/m的拉簧，与受电弓框架并联，实现将受电弓拉离接触网模拟转盘，并能保证升弓高在1.5 m左右时达到平衡。测试系统简图如图4所示。

图4 周期测量结构图

对受电弓框架上部横梁施加初始激励，横梁上的加速度传感器采集某一点信号，梯形积分处理得位移衰减曲线。测试结果及处理图像如图5所示。

图5 加速度传感器测得的加速度、时间图像(上图)及处理得到的速度、位移衰减曲线(中图、下图)

在MATLAB中编程处理得到周期T=1.294 s。综合用到以下公式

(2)

其中：ω2为框架质量块振动的角频率，推导得：

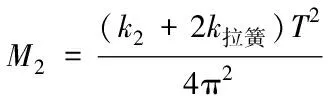
(3)

系统的刚度值为已经测得的框架本身的等效刚度和所加拉簧刚度的并联之和390 N/m。框架部分的等效质量还应该去掉夹具、未移除的上臂连接杆等。

保证1.5 m的升弓高度不变，进行多组试验，以增强测试结果准确性。将几组相似结果取平均值，得框架质量为16.54 kg。

利用自由振动衰减图像结合下式

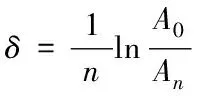
(4)

其中：A0，An为间隔n期的振幅。得到对数减缩率δ=0.5。

(5)

求出框架阻尼为12.783 N·s/m。

将弓头装上，用绳将框架固定住，依据同样原理获取弓头参数。得到受电弓的参数如下表1所示。

表1 受电弓模型参数

将所测受电弓质量块的等效参数补充进受电弓非线性方程中，至此，受电弓混合建模完成。

3 弓网耦合振动分析

3.1 改进的弓网耦合动力学模型描述

将改进的受电弓非线性模型代入目前广泛应用的受电弓二元归算质量块模型与接触网欧拉-伯努利梁的耦合模型中。

在作了一系列近似假设[13]后，考虑承力索、吊弦、支撑杆、定位器等参数，某锚段的弓网耦合优化模型如图6所示，具体参数详见文献[13]。

图6 某锚段的弓网耦合模型

在图中，L表示锚段的长度，TA和TB分别是承力索与接触线的张力，Mci、Mpi、Mdi分别为第i个腕臂与承力索之间的质量、第i个支撑杆与接触线之间的质量、第i个吊弦的质量，Kci、Kpi、Kdi对应为刚度，Cdi对应为阻尼，EIA和EIB分别为承力索与接触线的抗弯刚度，ρA和ρB对应于线密度。

弓网耦合模型接触网的主要参数如表2所示。

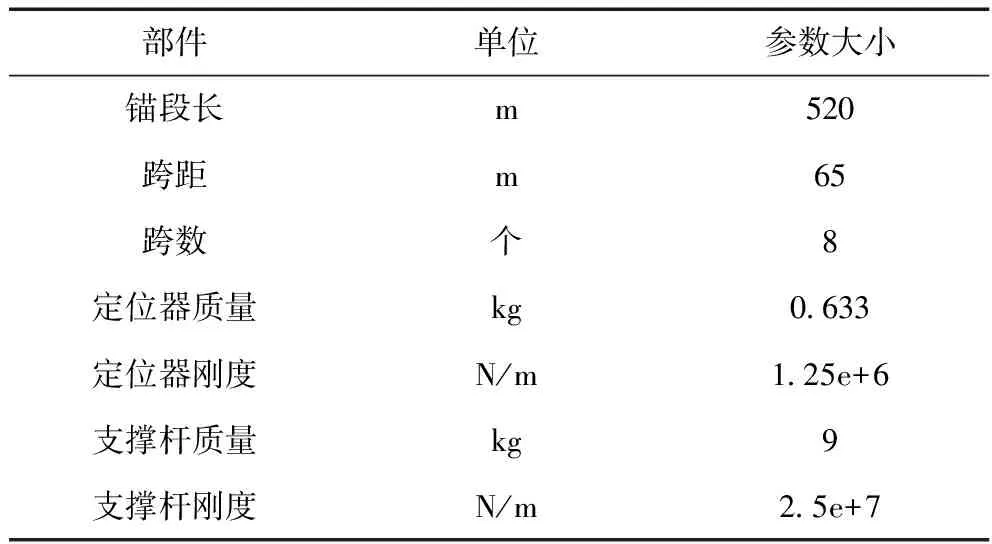
表2 接触网模型主要参数

接触刚度Kc=82300 N/m，将受电弓与接触网耦合在一起。同时，考虑到空气抬升力、车体振动的环境影响。

经工程试验模拟可知，受电弓的平均抬升力的目标值为[14]

Fm=F0+Faer=F0+kaerv2

(6)

其中，Fm为受电弓受到的总抬升力；Faer为受电弓受到的气动抬升力；kaer为空气阻尼系数，取值0.00097。

此外，用功率为0.01，均值为0.01的白噪声z模拟轨道不平顺造成的车体振动。

通过将能量等效原理与第二拉格朗日方程相结合，可以得到非线性受电弓—接触网系统耦合微分方程组。

(7)

图7 v=120 km/h模型改进前后对应的接触压力曲线

3.2 速度、物理参数对弓网接触力的影响

受电弓参数影响高速铁路接触压力平均值。标准偏差反映接触压力在动态接触压力平均值附近的波动情况。计算公式为：

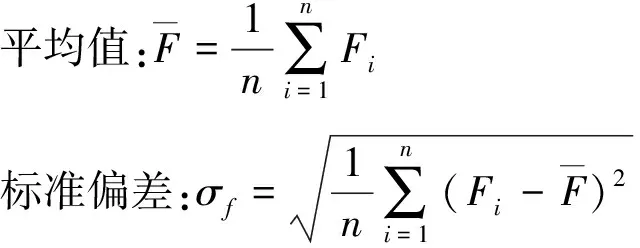
(8)

采用Newmark-β法编制数值仿真程序。图7图8分别为F0=100 N时，v=120 km/h，v=320 km/h对应的接触压力曲线。图7中接触力最大值和最小值都在规定范围内[7]，因此模型有效。

可以看出，接触力最大相差1.76 N，此时的弓头柔度、车体的振动、气动抬升力对接触力有较小的影响。但在图8中，与改进前模型对比，接触力最大相差13.94 N。可见高速运行时，非线性等因素不可忽略。

图9为改进前后两类模型对应的随速度变化的接触力标准差仿真结果。图10为改进后模型对应的随速度变化的弓网接触力性能指标仿真结果。F0=100 N，速度v=120 km/h，控制其它参数按给定参数条件不变，将弓头、框架的质量、刚度、阻尼线性参数按10%的比例增加并对两类模型下的接触力指标进行数值模拟，见图11。

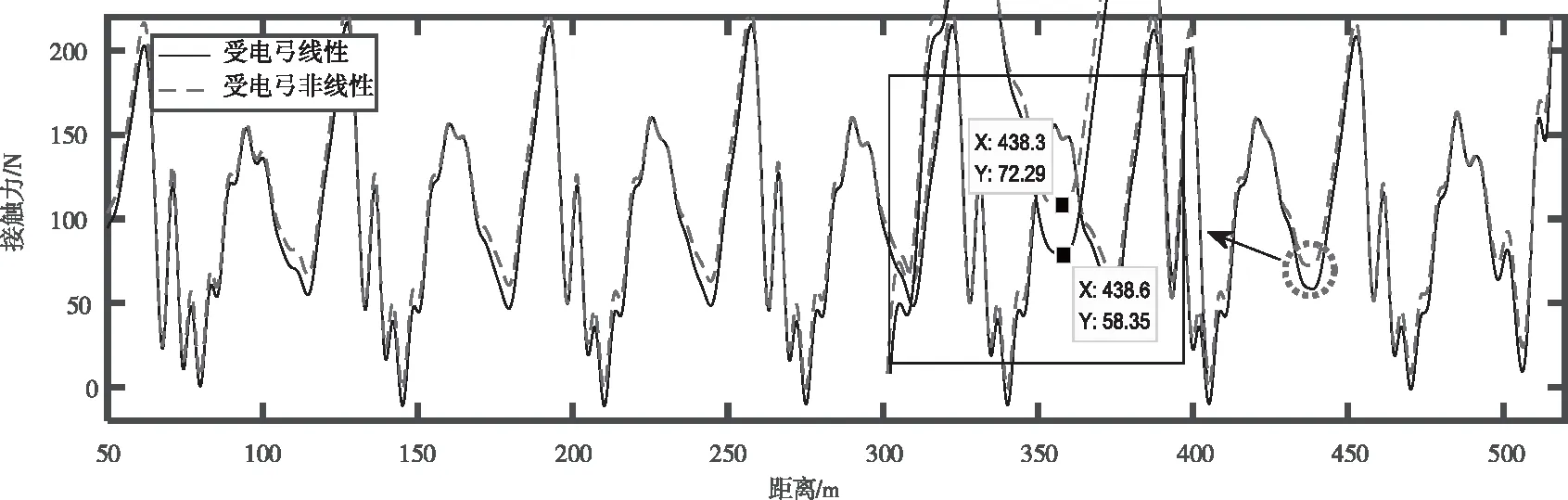
图8 v=320 km/h模型改进前后对应的接触压力曲线

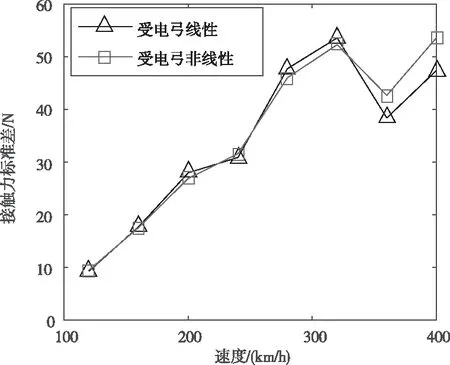
图9 不同运行速度下接触力标准差的计算结果

图10 不同运行速度下接触力的计算结果

图9表明，在给定模型参数和实测参数下改进前后两类弓网耦合模型在速度区间120 km/h - 260 km/h对应的接触压力标准差σf是接触压力平均值的10%-30%左右，说明所建改进前后非线性弓网耦合模型有效。同文献[7]中仿真数据进行比较，也验证了数值仿真的效果。在120 km/h-320 km/h的速度区间内，空气阻尼，接触网抬升量都在随速度不断变化的情况下，模型改进前后对应的σf差异并不明显，σf由10 N增加至50 N，反映出接触压力在动态接触压力平均值附近的波动加剧；超过320 km/h后，对应的σf差异增大，此速度前后σf会有明显的下降趋势。

从图10中看出，列车速度不断增加，弓网接触力最大值整体呈上升趋势，最小值呈下降趋势。接触力平均值在低速时基本保持不变，高速时则增率变大，整体变化相对接触压力最值不明显。当列车速度约为320 km/h左右时，弓网接触不稳定，容易发生拉弧等事故；当列车速度超过360 km/h，接触力急剧变化，因此需要严格控制列车提速至此危险速度。

图11中黑色实线表示模型改进前对应的接触力各项性能指标仿真结果，红色虚线表示模型改进后对应的接触力各项性能指标仿真结果。六次模拟再次证实，当列车以120 km/h的低速行驶时，改进前后模型对应的弓网接触力没有太大差异。其中性能指标Fmean变化不大。K1、C2的影响基本可以忽略，K2在参数变化的小范围内对接触力的影响也可被忽略，不然则需要被考虑。随M1、M2的增大，离线和磨耗的风险将增大，其中M2对应的Fmin值的变化幅度是M1的的2倍，因此在其它参数的给定条件下，框架质量是弓网离线的关键影响参数。而C1对应的Fmax值的变化幅度是M1和M2的2倍，因此弓头阻尼在其它参数给定条件下是弓网磨耗加剧的关键影响参数。

4 结论

本文为获得更加贴合实际的弓网耦合非线性模型，在参数获取上，基于实验室受电弓，摆脱实验室条件的局限，通过自由振动周期法等具有通用意义的实验方法，利用公式推导得出受电弓各项参数。对传统弓网耦合模型进行改进，将弓头柔性、接触网结构参数、空气抬升力和轨道不平顺引起的车体振动考虑进弓网耦合非线性振动分析中。

得出的结论有：

1)改进后的受电弓混合模型既没有归算质量模型简化程度过大，属于线性结构的局限，也比全柔性体模型具有更高的计算效率。改进后的弓网非线性耦合模型既可以简化计算又能更加反映工程实际。

2)弓网耦合模型改进前后在列车低速和高速时对应的接触力仿真结果最大差异值分别为1.76 N和13.94 N，因此高速运行时非线性等因素不可被忽略。随列车速度提高，弓网接触不稳定，易发生磨损或离线、拉弧现象。当列车速度超过360 km/h，接触力急剧变化，需严格控制列车提速。

3)弓头和框架质量、框架刚度、弓头阻尼是影响接触网系统与受电弓系统合理匹配的关键参数。其中框架质量和弓头阻尼分别是离线和磨耗现象的重要影响参数。在未来的受电弓研发以及改善受电弓受流质量的研究上应给予重点关注。