环量控制翼型非定常气动力建模

雷玉昌，张登成，张艳华

(1.空军工程大学 研究生院，西安 710051；2.中国人民解放军95034部队，百色 533600；3.空军工程大学 航空工程学院，西安 710038）

在航空技术应用中，使用环量控制技术作为主动流动控制的解决方案越来越引起人们的注意［1-2］。环量控制技术是指在翼型后缘表面开缝以形成沿着物面切向的射流，用以增加沿着翼型表面的环量，进而增加升力［3-4］。风洞试验和数值仿真结果表明，环量控制技术能够大幅度提高翼型升力，并在高升力条件下改善升阻比［5-6］。环量控制技术最初就是因为其卓越的高升力性能而引起关注，经过八十多年的发展，该技术逐渐在无尾飞行器的气动力控制、风力涡轮机的载荷控制、降低噪声、降低飞行器结构质量及提高隐身性能等方面表现出优越的性能［7-10］。特别是在无尾飞行器的控制方面，逐渐表现出了替代传统控制舵面的发展趋势。英国BAE系统公司先后试飞了“恶魔(Demon）”、“Magma”等技术验证无人机，利用环量控制技术进行了滚转操作，验证了环量控制射流替代传统舵面的可行性［11-12］。虽然已经证明了环量控制技术的相关优越性，但要实现可用的环量控制射流，还有很多关键理论和技术问题需要研究。其中考虑迎角改变时环量控制射流对于非定常气动力的瞬态反应是必不可少的。因为一方面环量控制射流并不能像传统舵面一样，在迎角改变时与翼型保持同步偏转，而是存在时间迟滞效应；另一方面高动量系数情况下会导致机翼提前失速，导致翼型在中小迎角下就会出现失速分离情况。因此，传统飞行器的非定常气动力模型将无法适用于环量控制飞行器。而飞机过失速机动时会产生流动分离和漩涡破碎，使得气动力和气动力矩呈现高度的非线性和非定常特性［13-14］。建立环量控制翼型在机动过程中的非定常气动力模型，对于准确理解射流作用机理及进行飞行控制系统设计具有重要意义。

目前，关于环量控制技术的研究中并未建立起高精度的非定常气动力模型。Loth和Englar等［15-16］给出了基于定常实验数据的曲线拟合公式，其中，文献［15］给出的经验公式在较低迎角、单射流情况下与可用实验数据有较好的一致性。Hoholis［17］针对二维环量控制翼型的气动参数进行了曲线拟合，并添加了稳定性导数以凸显其非定常效应，结果表明，该方法对升力和力矩系数预测结果较好，对阻力系数预测较差，而且并不能准确预测非定常效应的气动力迟滞效应。Krukow和Dinkler［18］在进行环量控制机翼的气动弹性研究中利用高阶多项式拟合得到了定常气动力模型。Semaan等［19］使用LASSO方法辨识了周期性射流和脉冲型射流叠加后对机翼升力系数的增量影响。综上所述，目前对于环量控制飞行器气动力模型的建立多集中在定常模式下，对非定常气动力模型的研究较为匮乏。而传统飞行器非定常气动力建模的发展已经历经了几十年，逐渐发展形成了气动导数模型［20］、状态空间模型［21］和微分方程模型［22］等数学模型和模糊逻辑模型［23］、神经网络模型［24］等人工智能模型。这些模型都能在一定程度上描述传统飞行器在大迎角下的非定常气动力变化趋势。

因此，本文借助高精度的数值仿真技术，分析环量控制翼型非定常流动状态。基于微分方程模型，添加环量控制射流参数源项。通过两步线性回归参数辨识方法建立适用于环量控制翼型的非定常气动力数学模型，并对高动量系数下的非线性影响进行修正。通过对任意条件下的非定常流动充分建模，用于环量控制技术的非定常状态研究。

1 数值计算方法与验证

1.1 计算模型和网格

超临界翼型有着钝前缘、大厚弦比的特点，内部能够容纳环量控制技术所需要的供气机构或管道等，因而成为环量控制技术良好的研究翼型。本文采用修形过的超临界翼型进行相关研究。翼型相对厚度为17%，弦长c＝240 mm。采用文献［25］中的修形方法，将距后缘25%弦长的部分修形处理，按照后缘半径r／c＝2%绘制柯恩达后缘曲面，射流口高度h＝0.001c。图1为修形过的超临界翼型示意图。计算区域选取翼型弦长的30倍，网格剖分时采用结构网格，生成O型网格拓扑结构，边界层内第1层的网格高度约为1×10－5m，射流口附近第1层网格高度为2×10－6m，保证第1层高度的y＋均小于1，以满足黏性底层的计算要求。网格总数约为58万，进行非定常计算时采用FLUENT网格动态重构技术，图2为翼型网格划分及非定常计算过程迎角α从－5°变化到5°翼型后缘网格变形情况。可以看出，网格适应情况较好。

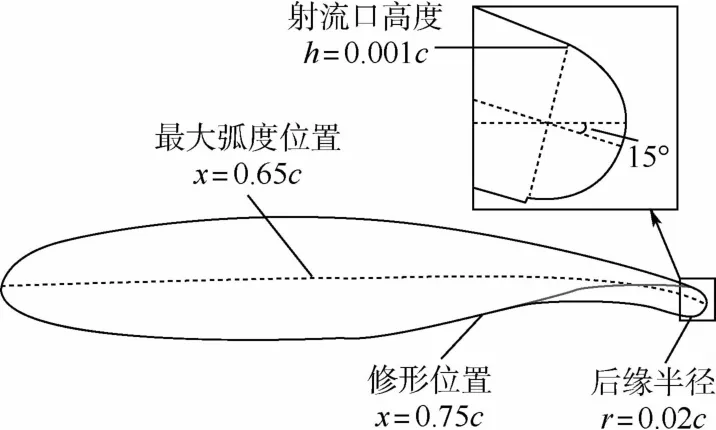
图1 修形后的超临界翼型Fig.1 Supercritical airfoil after modification

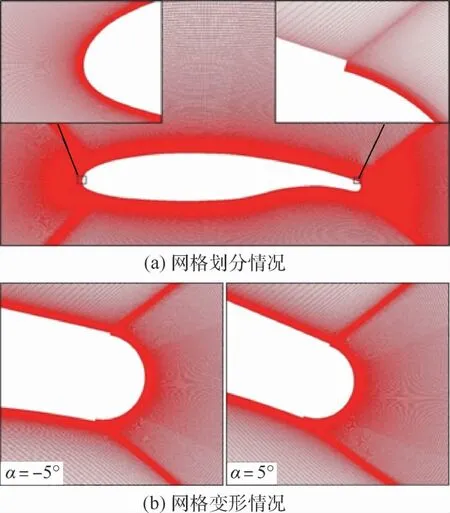
图2 翼型计算网格Fig.2 Airfoil’s computational grid

1.2 计算方法和验证

本文的数值模拟方法采用二维雷诺平均Navier-Stokes方程，其积分形式为

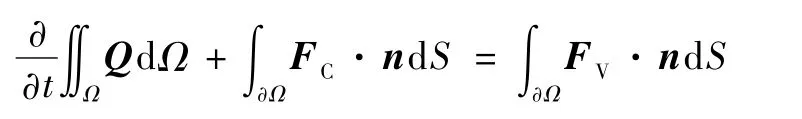
式中：Q为流动变量；Ω为控制体；FC和FV分别为无黏性通量和黏性通量；n为控制体面的外法线向量。采用k-εSST湍流模型，该模型对于有较大逆压梯度的边界层流动、分离预测性能较好。采用有限体积法离散控制方程，黏性通量采用二阶迎风格式离散。远场边界为压力远场，壁面边界采用无滑移壁面条件。

本文采用的数值仿真软件为商用软件FLUENT。采用的求解器为基于Simple方法的Pressure-Based Solver。对求解不可压缩流动及微可压流动效果较好。该方法对于非定常问题的流动计算，主要借助隐式时间积分方案，在每个计算时间步内进行迭代，在计算步之内的内迭代计算与普通稳态问题的内迭代计算是相类似的，在得到本时间步内的收敛解之后，转入下一个时间步进行继续计算。

为了验证本文所采用数值计算方法的准确性，分别对标模NACA0012翼型强迫俯仰振动下的非定常气动力数据及环量控制翼型在射流吹气下的定常气动力数据进行对比验证。

对于标模NACA0012翼型而言，计算过程中强迫翼型绕重心做俯仰振荡，其迎角变化规律为

式中：减缩频率k＝ωc／(2V）∞，c为弦长；V∞为来流速度为无量纲时间；α0为基准迎角；αm为振幅。减缩频率用来描述翼型的振荡频率。计算条件：k＝0.081 4，α0＝0.016°，αm＝2.51°。本文计算时采用的物理时间步长t＝0.01T，内迭代步数为50，其中T表示翼型非定常运动周期。为加快收敛，初始解从中心迎角处的定常收敛解开始计算。将计算结果与文献［26］中Landon的实验结果和Uygun的数值仿真结果进行对比，结果如图3所示。图中：CL为升力系数，α为迎角。在部分迎角下，仿真结果与实验数据存在差异，但是在总体上与实验数据是一致的，能够反映非定常流动时的气动力变化趋势。

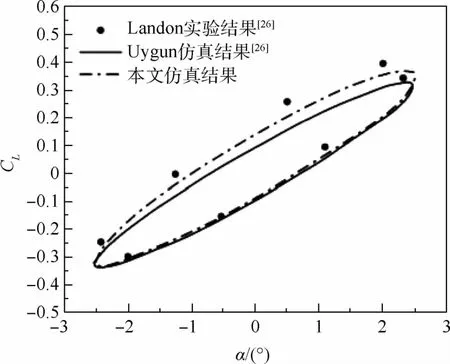
图3 NACA0012翼型非定常升力系数仿真与实验对比Fig.3 Comparison of simulation and experimental results of unsteady lift coefficient of NACA0012 airfoil

对于环量控制翼型而言，动量系数是影响环量控制中后缘射流控制效果的重要参数，升阻特性受动量系数影响较大，其定义为

式中：m˙为射流出口处的质量流量；Vjet为射流速度；ρ∞为来流密度；V∞为来流速度；S为二维翼型单位展长的面积，在数值上等于弦长c。假定气流等熵膨胀至射流出口，远前方来流静压为射流出口静压。通过调节射流出口速度，调节射流出口处的质量流量和动量系数。本文将使用上述参数作为后缘射流的边界条件，调整参数以进行相关研究。对0°迎角下不同吹气动量系数下的环量控制翼型进行数值模拟。计算条件为：来流速度为30 m／s，来流温度为293.15 K，雷诺数为5×105，动量系数在0～0.06之间变化。将仿真结果与文献［25］中的实验数据进行对比，仿真采用稳态方法，结果如图4所示，仿真结果与实验数据基本吻合。综上所述，本文采用的数值计算方法应当能够较好地模拟环量控制翼型的非定常气动力数据。

图4 环量控制翼型升力系数仿真与实验对比Fig.4 Comparison of simulation and experimental results of circulation control airfoil’s lift coefficient

2 定常气动力插值

借助数值仿真或风洞试验手段得到的翼型以迎角作为自变量的气动参数往往具有极大的离散性和不完整性，因此，在进行气动力和力矩建模时需要对离散的气动力数据进行拟合或插值，使之成为光滑的连续函数。本节基于Kriging模型对定常状态下的环量控制翼型气动力进行插值处理，并与传统气动导数模型的预测精度进行对比。

2.1 K riging模型

Kriging模型最初是由南非采矿工程师Krige在1951年提出的一种空间估计技术，最初应用于矿床储量计算和误差估计，经过几十年的发展，逐渐在地质、气象、航空航天、汽车等领域得到发展和应用［27］。Kriging模型由于其卓越的非线性函数插值预测能力和误差估计功能，正在受到越来越多的关注。

设m1，m2，…，mn为数量集上的一系列变量值。z(m1），z(m2），…，z(mn）为相应的参数值。则Kriging模型定义变量 m0处的插值结果z*(m0）为已知样本值的线性加权，即

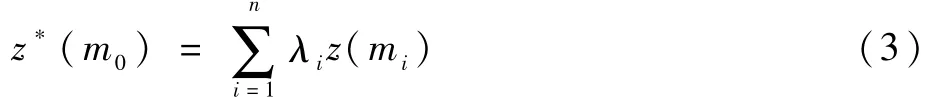
因此，通过求解加权系数λi就可以得到数量集中任意位置的参数估计值。关于Kriging模型的详细介绍和推导参见文献［27］。

影响环量控制翼型定常气动力的主要因素包括迎角α和动量系数Cμ。仿真计算了α为－5°～15°，Cμ为0～0.06之间的气动力参数。

环量控制翼型的气动力参数呈现高度的非线性特征，迎角α和动量系数Cμ对气动力的影响高度耦合，翼型失速与动量系数大小密切相关，动量系数越大，翼型失速迎角越小。以其气动力参数可作为两者的空间分布变量。选取样本数量集α为－5°～15°，Cμ为0～0.06之间的离散气动力参数。对样本数量集进行归一化后利用Kriging模型分不同方向进行函数计算，其预测结果和均方根误差结果如图5和图6所示。

图5 Kriging模型预测结果Fig.5 Prediction result of Kriging model

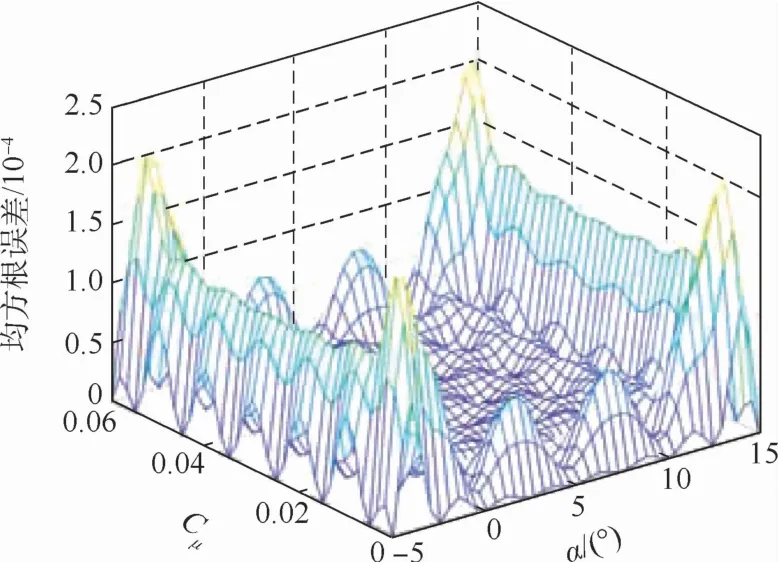
图6 Kriging模型预测误差Fig.6 Prediction error of Kriging model

从整体上来看，Kriging模型对于环量控制翼型的定常气动力插值结果精度较高，特别是对于采样点范围内的内插结果误差值低于1×104。对于边界值误差较高，这反映了模型对气动力参数的外插能力需要进一步提高。Kriging模型能够实现环量控制翼型气动力参数设计的光滑连续插值，且具有较高的预测精度。

2.2 传统气动导数模型

传统的气动导数模型是基于线性叠加原理，假设气动力可由飞行器迎角、舵面偏角、角速度等状态变量线性叠加，其本质是气动力的泰勒展开式分解后只保留其一阶表达式，保留的各状态变量系数分别被称为气动静、动导数。对于定常气动力而言，仅涉及气动静导数。为了提高气动导数模型在大迎角非线性情况下的预测精度，一般采用高阶展开式进行拟合，以升力系数为例可以表示为

将射流的影响分为两部分：一部分设置为初始状态量，包含在系数f0中，另一部分用于修正迎角带来的气动力影响，包含在系数f1和f2中。将系数fi设置为射流动量系数的三次多项式函数：

分别在不同的吹气动量系数下验证Kriging模型与传统气动导数模型的准确性，将2种模型的预测结果与CFD数值计算值进行比较，图7给出了不同动量系数下2种模型的预测情况。

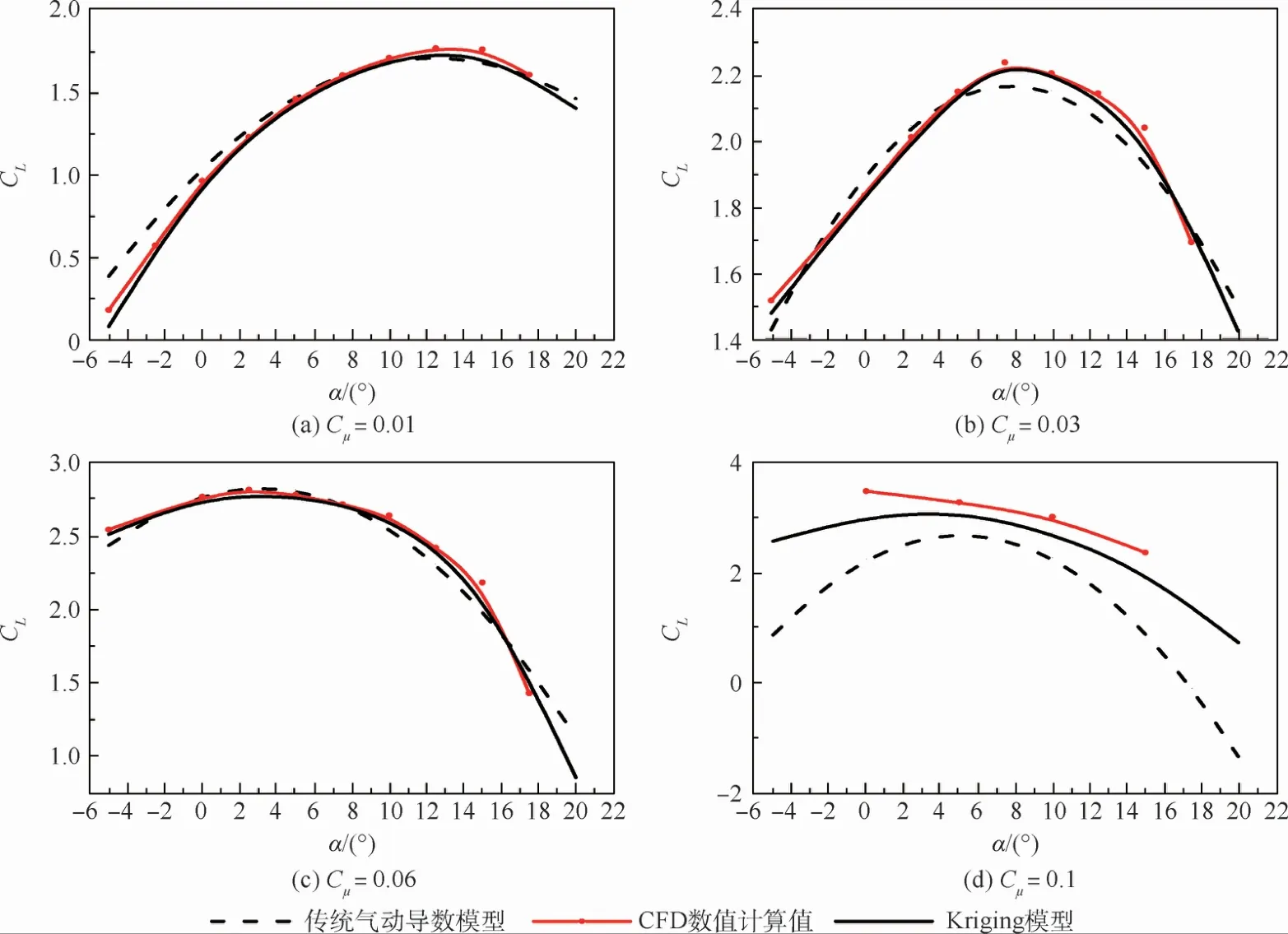
图7 Kriging模型与传统气动导数模型对比结果Fig.7 Comparison between Kriging model and aerodynamic derivative model

从图7中可以看出，在采样范围的动量系数(Cμ为0～0.06）作用下，Kriging模型较传统的气动导数模型预测精度有明显提升，预测结果更加接近CFD计算值，并能准确预测失速迎角范围；对于采样范围之外的参数，Kriging模型仍然能保持一定的预测精度，预测效果较传统气动导数模型有较大提升。

3 非定常气动力建模

环量控制射流相较于传统舵面而言可以大幅度提高翼型升力、改善升阻比，这使得环量控制飞行器往往在小迎角下就能够获得传统飞行器在大迎角下的气动力特性。因此，本文主要进行中低迎角(－5°～10°）下的环量控制翼型非定常气动力建模。

3.1 环量控制翼型非定常气动力模型

在机翼小振幅强迫振荡风洞试验中，若还未出现深动态失速现象，则根据小扰动假设，气动力参数可以由高阶线性状态方程表示，包括定常和非定常两部分［28］。其中定常气动力反映了机翼振荡过程中的气动力快速响应部分，非定常气动力部分则反映了机翼运动导致的流场内涡系移动产生的气动力迟滞效应。已有的研究表明［29］，环量控制射流通过改变翼型表面压力分布、控制分离点移动而改变气动力系数，这与迎角对气动力系数的作用机理一致。对于环量控制翼型而言，动量系数与迎角共同影响翼型的气动力系数，并且呈现高度耦合。以纵向运动为例，气动力参数可以表示为

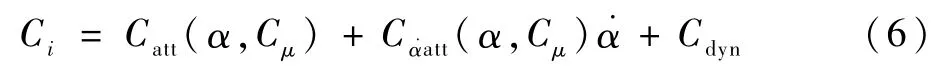
式中：Ci为气动力力矩系数；Catt(α，Cμ）为气流在附着流动的状态下，即无分离假设下的气动力系数；Cα˙att(α，Cμ）为机翼定常俯仰下的气动力导数，为迎角变化率；Cdyn为非定常气动力增量。

上述模型适用于尚未出现深动态失速时的气动力系数变化情况，其中，Cdyn采用以下线性微分方程式表示：

式中：τ为非定常运动中的特征时间常数；Cst(α，Cμ）为实际定常状态下气动力系数，即Kriging模型预测值；ΔC(α，Cμ）为由于气流分离导致的定常气动力增量。

对于环量控制翼型而言，假设在迎角俯仰过程中射流动量系数不变，这种假设是合理的，目前对于传统舵面飞行器在大迎角下非定常气动力模型的建立也是基于舵面偏角不变的情况。

3.2 非定常气动力模型参数辨识

借助经典的强迫振动法计算谐振运动过程中的非定常气动力，强迫翼型绕重心做小幅度的俯仰振荡，其迎角变化规律为

式中：Δα为迎角改变幅度。

非定常气动力系数可以看做时间¯t的连续函数，因此，可以将翼型小幅度俯仰振荡过程中的气动力系数变化按照减缩频率进行傅里叶分解，以升力系数为例，保留一阶形式可以表示为

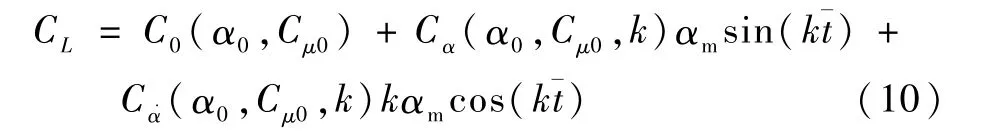
式(10）表示了气动力系数可类似于“小扰动”假设，由基准系数加上扰动系数构成。其中，C0(α0，Cμ0）表示中心迎角对应下的基准气动力系数；Cα(α0，Cμ0，k）称为同相导数；Cα˙(α0，Cμ0，k）称为异相导数。

基于小振幅情况下的线性假设：

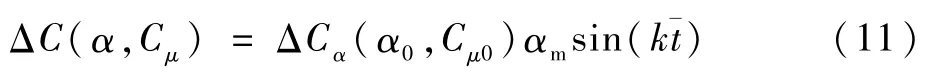
该假设表示在小振幅情况下实际静态气动力系数与气流不分离假设下静态气动力系数之量与迎角变化近似呈现线性关系。ΔCα(α0，Cμ0）表示该差值与迎角变化之间的导数。

借助欧拉方程求解微分方程式(7），即求解下述方程组：

使用微分算子法容易解得方程组(12）的解，将式(8）、式(9）的迎角变化规律代入式(6）中，与式(10）的相关系数作对比后整理得到以下关系：

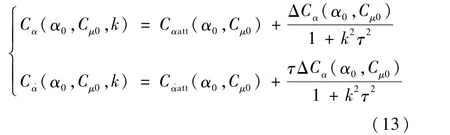
由上述推导可知，同相导数并不等同于静导数，异相导数也并不等同于动导数。

但是当τ非常小时，此时同相导数和异相导数分别退化为传统线性气动导数模型的静导数Cαst(α0，Cμ0）和动导数Cα˙att(α0，Cμ0），即如下关系式：

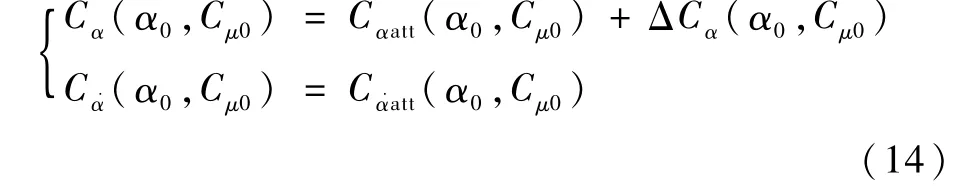
式中：Cα(α0，Cμ0）＝Cαst(α0，Cμ0）。

此时，Cdyn(0）＝0，C0(α0，Cμ0）＝Cst(α0，Cμ0）。

τ定量地表征了翼型非定常气动力效应的显著程度。解式(13）可得

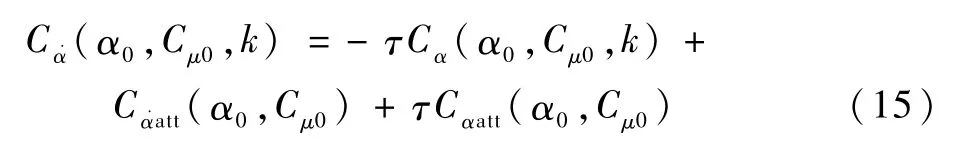
由于在同一中心迎角、不同减缩频率对应下的同相／异相导数数据点落在同一条直线上，而直线的斜率则表示特征时间常数的负值：－τ。

对于某一特定中心迎角下的小振幅强迫振动数据而言，采用最小二乘法可得到对应中心迎角下的同相／异相导数数据点，部分数据点如图8所示。

图8 不同迎角、减缩频率下的同相／异相导数Fig.8 In-phase and out-phase derivatives at different angles of attack and reduced frequencies

由上述分析可知，对于特定的小振幅流动状态(特定的迎角和动量系数）下，τ是固定的，计算得到的不同中心迎角、动量系数下的特征时间常数如图9所示。

图9 时间常数随动量系数的变化曲线Fig.9 Variation curve of time constantwith momentum coefficient

特征时间常数值受迎角和动量系数影响较大。总体来看，τ随Cμ增大呈现先降低后增加的趋势，这说明低动量系数下，翼型的非定常气动效应减弱，但是当动量系数增加到一定值后，翼型的非定常气动力效应增强，并且随着迎角的增大，该临界动量系数逐渐降低。当α0＝0°时，在全动量系数范围内时间常数趋于0，气动力模型可近似用传统线性气动导数模型代替。当α0＝10°时，在全动量系数范围内时间常数都较大，翼型处于临近动态失速或失速后状态，此时翼型的非定常气动力特性主要由后缘涡系的迟滞运动导致，传统线性气动导数模型不再适用。

对于τ较小的情况，基于传统线性气动导数模型，使用不同迎角和动量系数下非定常运动的若干离散点，借助最小二乘法辨识静导数Cαst(α0，Cμ0）和动导数Cα˙att(α0，Cμ0）。

对于τ较大的情况，由于无法使用传统的线性气动导数模型，在获得τ(α，Cμ）后，仍需要辨识同相／异相导数中的Cαatt(α0，Cμ0）、ΔCα(α0，Cμ0）和Cα˙att(α0，Cμ0）。

为了便于描述，将式(13）用以下方程描述：

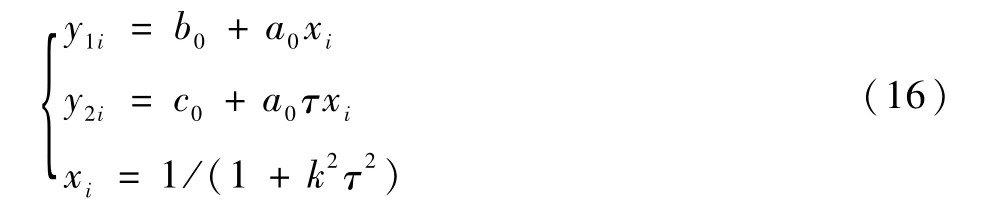
式中：y1i、y2i、b0、a0、c0分别为式(13）中的相关参数。为了辨识相关参数，引入以下误差函数：

式中：n为同一中心迎角和动量系数、不同频率下的仿真实验次数；y1i和y2i分别为特定小振幅流动状态下的同相／异相导数；b0、a0和c0为参数辨识后的相应值。该方法的核心思想是两步线性回归法，即先根据非定常运动的离散点辨识得到y1i和y2i，再根据得到的y1i和y2i辨识b0、a0和c0。辨识过程中，因为存在中心迎角、动量系数、减缩频率3个自变量，直接进行参数辨识需要耗费极大的仿真计算量，所以本节针对射流动量系数与迎角的相互作用特点，对b0、a0和c0做合理优化，提高计算效率。

对于b0而言，Jones［25］曾指出动量系数对气动力的影响呈现2个比较明显的线性阶段，其流动状态满足无分离假设，因此在低动量系数下b0可以用以下关系式代替：

式中：CαCμst(α0）为Cαst(α0）对Cμ的导数，可直接由Kriging模型插值得到，待辨识参量变为迎角。采用这样的简化方法在低迎角线性阶段可直接退化为Cαst(α0，Cμ0），与无分离情况下的气动导数一致。

对于c0而言，当自由来流不发生变化时，迎角俯仰导致翼型表面产生绕重心的旋转速度，与外流相对流动产生下洗效应，而后缘射流并不会直接随着翼型俯仰，而是由于后缘压力场的变化时刻处于动态平衡之中。由定常旋转产生的准定常气动力增量主要在小迎角时起作用，与迎角变化率近似呈线性关系。在较大迎角范围内，其引起的准定常气动力增量远小于非定常气动力增量。将动量系数作为修正参数，可以将c0表示为

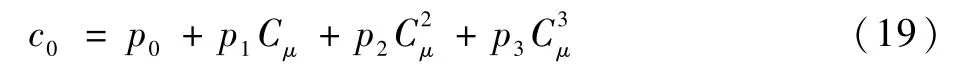
对于a0而言，a0＝Cst(α，Cμ）－Catt(α，Cμ），因此只需辨识b0即可。在辨识得到τ和ΔC(α，Cμ）后，根据非定常气动力增值周期性变化的特性，即Cdyn(0）＝Cdyn(2π／ω），即可求得初值Cdyn(0）。

以误差函数E最小为优化目标函数，以升力系数为例，得到的Cαatt(α0，Cμ0）曲线如图10所示。

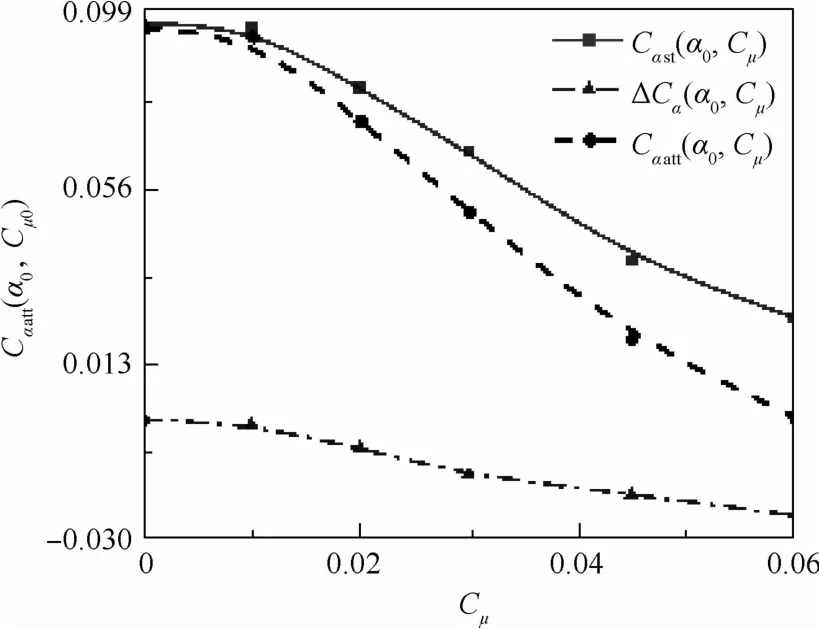
图10 Cαatt(α0，Cμ0）的辨识结果Fig.10 Identification results of Cαatt(α0，Cμ0）

3.3 非定常气动力模型与仿真数据对比验证

为了验证上述非定常气动力模型的准确性，分别对环量控制翼型在不同迎角、动量系数、振幅下的预测结果进行对比分析。预测结果取升力系数CL和俯仰力矩系数Cm进行对比分析。计算条件为：来流速度为30 m／s，来流温度为293.15 K。中心迎角、动量系数、振幅、减缩频率验证如图11、图12所示。

如图11所示，为了得到非定常气动力模型对大振幅情况下的预测结果，将大振幅的流动情况分段处理，每一段的气动力变化情况都可以用小振幅情况下迎角对应的同相／异相导数表示，分段处理后可以将大振幅情况下的预测结果近似表示为

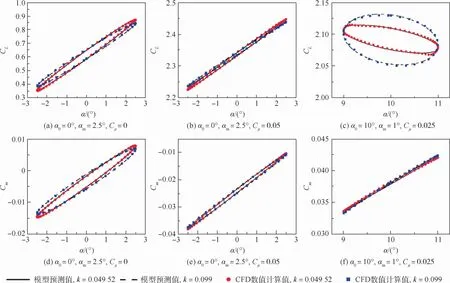
图11 小振幅流动状态下结果对比Fig.11 Comparison of results under small-amplitude flow

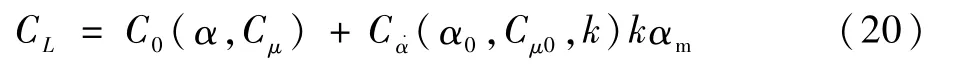
将分段处理的αm取为1°，得到非定常气动力模型对于大振幅情况下的预测结果，如图12所示。

图12 大振幅流动状态下结果对比Fig.12 Comparison of results under large-amp litude flow

可以看出，对于升力系数而言，线性非定常气动力模型对小振幅情况下流动状态有较好的预测精度，特别是在0°迎角下，此时升力系数线性特征明显，在较大振幅情况下(见图11(a）、图11(b））也能够取得较好的预测精度。但是在较大迎角、较高动量系数的流动状态下，如图12(c）所示，此时升力系数非线性特征明显，线性非定常气动力模型难以取得较高的预测精度。对于俯仰力矩系数而言，线性非定常气动力模型在各个动量系数下都能较好地预测力矩系数变化趋势。这是因为俯仰力矩系数主要受翼型上表面分离涡影响，当翼型上表面分离涡移动时，对应的负压区逐渐扩大或者缩小，导致俯仰力矩系数变化。高动量系数下翼型上表面不再分离，导致迟滞效应逐渐减弱。值得一提的是，在出现动态失速分离前，高动量系数具有减弱气动力迟滞效应的优势，如图11(f）、图12(f）所示，此时俯仰力矩的变化几乎不存在迟滞效应，与定常状态下的变化几乎一致。在出现动态失速后，同样能在线性小迎角阶段减弱迟滞效应，如图12(b）、图12(c）所示。

3.4 非定常气动力模型非线性修正

当振荡幅度增大并出现深动态失速的情况时，上述线性非定常气动力模型将会在失速段失去预测精度。这是因为在大振幅情况下进行分段处理完全忽略了洗流时差的累计效应，在非线性较为明显的阶段将完全丧失其预测精度。为了改善非定常气动力模型在动态失速情况下的预测精度，采用文献［30］的方法将非定常气动力增量式(7）改写为以下非线性形式：

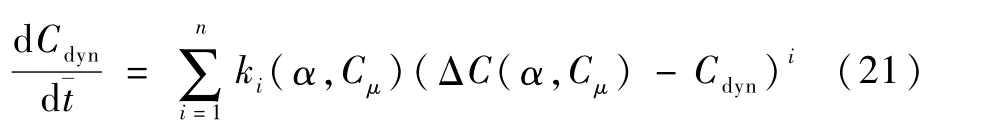
式中：ki(α，Cμ）＝1／τi(α，Cμ），该方法采用多次逼近的思想，避免了大振幅过程中仅用单一时间常数τ线性表示增量的误差，同时充分考虑了累计效应。利用上述线性非定常气动力模型辨识得到的Catt(α，Cμ）和Cα˙att(α，Cμ），可以获得线性假设下CL的变化，与实际CL的差值即非定常气动力增量，与线性假设下得到的Cdyn相叠加即实际情况下的Cdyn，保持ΔC(α，Cμ）和k1(α，Cμ）不变，利用最小二乘法即可辨识得到ki(α，Cμ），采用这样的假设能够有效降低参数辨识的难度。

上述线性非定常气动力模型已经能够满足无射流情况下中低迎角的大振幅预测精度，因此，非线性项主要用来提高高动量系数情况下的预测精度。为了提高辨识效率，本文仅对包含Kriging模型中静态失速点附近的流动状态进行参数辨识。采用三次非线性形式描述非定常气动力增量，辨识得到的k2(α，Cμ）和k3(α，Cμ）如图13所示。

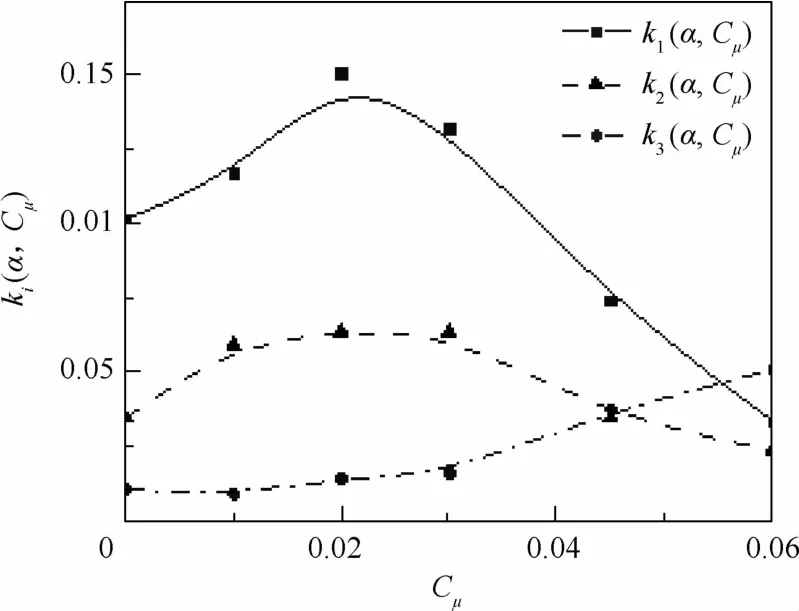
图13 ki(α，Cμ）辨识结果Fig.13 Identification result of ki(α，Cμ）

非线性项修正后的非定常气动力模型进行大振幅流动情况下的升力系数预测，结果如图14所示，其结果较线性模型有明显提升。

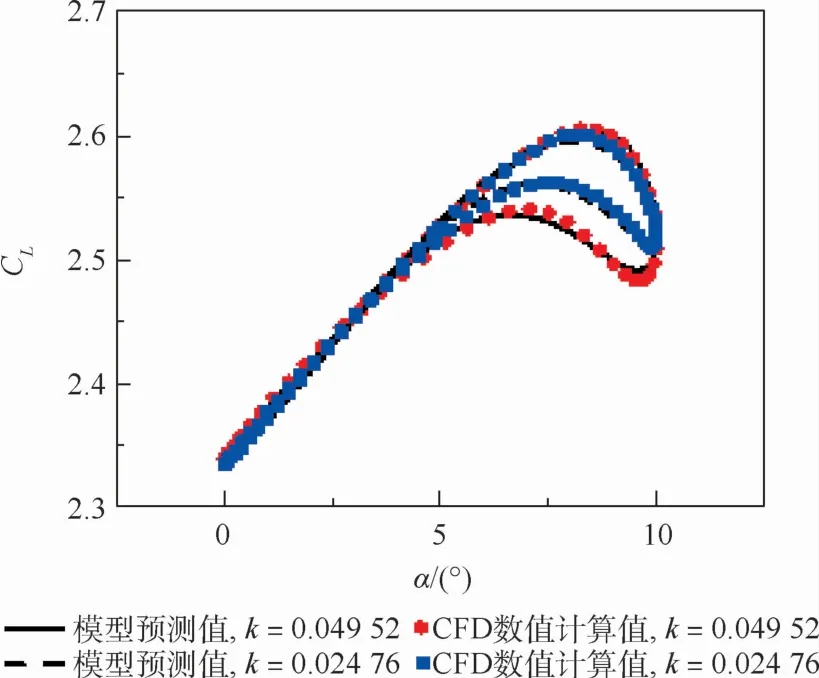
图14 非线性非定常气动力模型结果对比(Cμ ＝0.05）Fig.14 Comparison of results of nonlinear unsteady aerodynamic models(Cμ ＝0.05）

4 结论

本文主要进行了环量控制翼型非定常气动力的建模，通过上述分析，可以得到以下结论：

1）基于Kriging模型完成了环量控制翼型的定常气动力插值，能够精确的反映其定常气动力变化，插值精度要优于传统气动导数模型。

2）基于微分方程模型，通过添加射流参数源项，完成了适用于环量控制翼型的线性微分方程建模。对Cαatt(α0，Cμ0）和Cα˙att(α0，Cμ0）等参数简化处理，提高辨识效率。

3）对高动量系数情况下的非定常气动力模型进行非线性修正，能够较为准确的反映不同动量系数下的非定常流动特性。

4）对于升力系数而言，线性非定常气动力模型能够满足小振幅和低动量系数下大振幅流动状态；对于俯仰力矩系数而言，线性非定常气动力模型能够满足大部分流动状态。

环量控制翼型的非定常气动力耦合特性复杂，仍需要在以下方面进一步研究：①高动量系数下缺乏足够精度的数学模型来描述后缘涡的分离变化，需要对流场特性进行更深入的研究，进而优化模型结构。提高在高动量系数下非线性非定常气动力模型预测效果。②关于环量控制翼型的非定常气动力建模研究仍处于起步阶段，如何有效的结合已经较为成熟的大迎角非定常气动力数学模型是未来研究的途径之一。