疲劳统计学智能化中的高镇同法

徐家进

(力中国际融资租赁有限公司，广州 510620）

《疲劳应用统计学》［1］是高镇同先生在30多年前写的一本书，将统计学正式引入了解决各种疲劳问题的工程实践之中，建立了疲劳统计学这一学科［2］。

疲劳统计学是疲劳可靠性的理论基础，对于解决各类可靠性问题，特别是航空工业领域，其意义无论怎样强调都不为过。在疲劳统计学中，有一个非常独特而重要的统计分布就是威布尔分布。事实上，威布尔分布是疲劳统计学的一个最主要的内容之一。威布尔分布一个非常重要的特点就是具有最小寿命这个参数。但高镇同先生指出，最小寿命这个提法是不够全面的，因为按照威布尔分布的定义，应用于疲劳寿命时可明确为100%的可靠度之下的安全寿命。此提法是科学的，以后在疲劳统计学中就将这个参数改称为安全寿命。而这个参数对于像飞机这样产品的定寿起了关键性的作用。问题是威布尔分布的数学形式比较复杂，特别是在当时计算机的性能、使用和普及远远不如现在的情况下，使用起来比较困难。尽管目前已有了不少关于威布尔分布应用的软件，但绝大部分是二参数威布尔分布［3］，恰恰将安全寿命这个参数归零了。这样的简化显然是不合情理的。同时，高镇同先生强调威布尔分布是一种全态分布，既包括正态分布，也包括偏态分布。但因为威布尔分布的复杂性影响了它的推广和使用。因此，疲劳统计学智能化的当务之急就是要解决威布尔分布3个参数的估计问题。本文提出了与已有估计威布尔分布3个参数的2个方法不同的智能化解决方案

1 疲劳统计学的特点

疲劳统计学是将统计学原理应用到结构疲劳这个领域中去。三参数威布尔分布可以更好地描写结构疲劳寿命的特点，在疲劳统计学中具有非常重要的地位。但三参数威布尔分布并不为大家所熟知，这是因为其数学形式比较复杂，而且通过样本来确定其3个参数比较困难，应用起来也就有一定的难度［4-6］。自然也与对威布尔分布的意义认识不足有关，为此有必要先简要介绍一下威布尔分布的特点。

2 威布尔分布的特点

威布尔分布概率密度函数［1］为

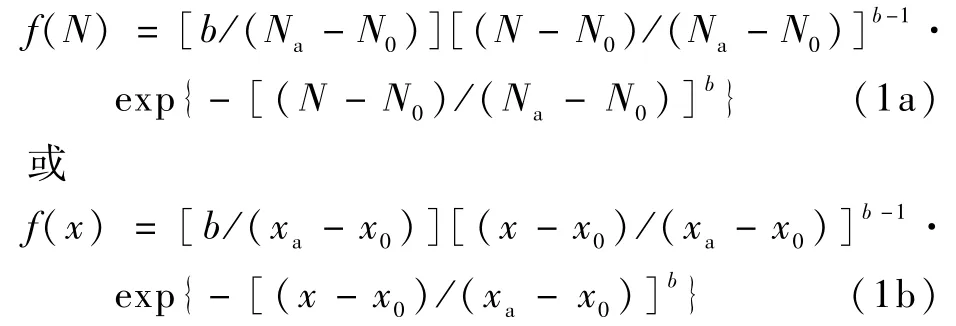
式中：N为疲劳寿命；N0为安全寿命；b为形状参数；Na为特征寿命；xa为特征参数；x0为位置参数；且0≤x0≤x＜∞。

为方便可设：

式中：λ为尺度或比例参数。

从统计分布角度看，由尺度参数λ代替特征参数更有一般性。这是因为x0＝0时，λ＝xa。即λ可看成x0＝0时的特征参数。因此，将式(3）代替式(1b）作为一般的三参数威布尔分布表达式。三参数分别为形状参数b、尺度参数λ和位置参数x0。

进一步，若设x0＝0，式(3）则为两参数威布尔分布概率密度函数。

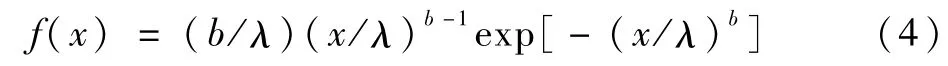
再设λ＝1就成了“标准”(一个参数）的威布尔分布概率密度函数。

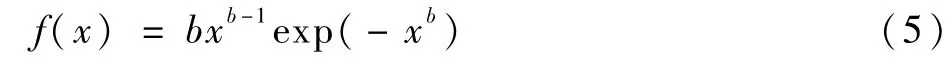
对于标准化的威布尔分布，b分别为0.5，2，3.5，5时，威布尔分布概率密度函数如图1所示。

由威布尔分布概率密度函数及图1可看出其有如下特点：

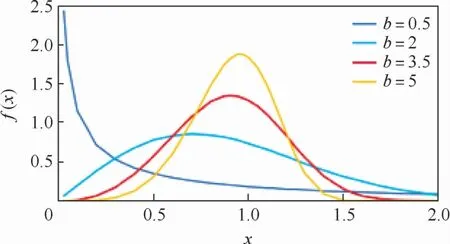
图1 标准威布尔分布概率密度函数Fig.1 Standard Weibull distribution probability density function

1）b为威布尔分布的形状参数是名至实归的。0＜b＜1时类似1／x函数，而1＜b＜3是左偏分布，3＜b＜4则近似正态分布，b＞4则为右偏分布。此外，当b＝1时为指数分布，b＝2时为瑞利分布。这也是高镇同先生为什么称威布尔分布为“全态分布”的主要原因。

2）威布尔密度函数有3个参数，比正态分布多1个，这是其优点(可描写安全寿命）但也是其缺点(数学形式比较复杂）的来源。正态分布能很好地描写对称状态的数据，问题是在现实生活中真正对称的数据只是一种理想状态，因此正态分布往往只是一阶近似。而威布尔分布既能描写对称状态(尽管是近似的），又能描写左偏或右偏的数据，故其应用范围要比正态分布大得多。

上文对威布尔分布做了定性的描述，现进一步对其做定量的研究。为方便，开始时仅对标准威布尔分布进行比较详细的研究，而二参数和三参数的威布尔分布均可得到类似的结果。

1）威布尔分布概率密度函数是满足归一化条件的。即要证明：

可设z＝xb，式(6）左边可变为

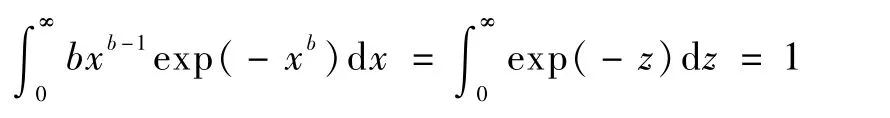
对于两参数和三参数的威布尔分布同样可得到这个结论，只要分别设：

2）容易证明，威布尔分布函数为

事实上，和1）相同可设z＝xb：

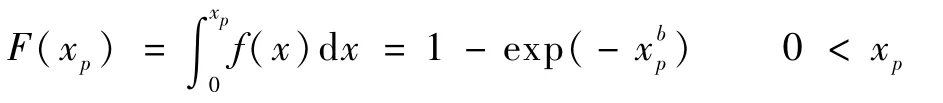
这个分布函数恰恰就是破坏率，而可靠度P为

式(9a）给出了可靠度的函数形式，对于应用有重大意义。即xp为与可靠度P相应x的值。两参数和三参数威布尔分布分别为

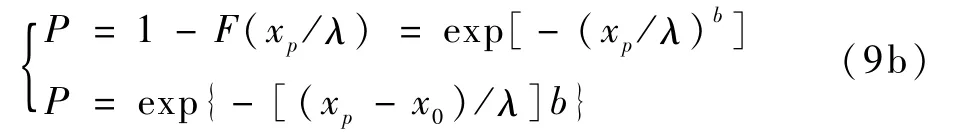
若此时取xp＝xa，xp－x0＝(x0＋λ）－x0＝λ，则

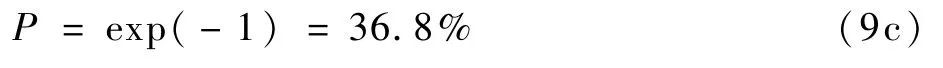
这表明任何威布尔分布当其值为特征参数时可靠度一定为36.8%，这是特征参数xa的一个物理意义。而取xp＝x0时P＝100%，也是参数x0为100%可靠度的安全寿命的由来。顺便指出，对于正态分布不可能有这个概念，因其左侧与水平轴不相交。

3）当b＞1时密度函数是凸函数，因此必有一个极(大）值。事实上：

令f′(x）＝0，即有b－1－bxb＝0。

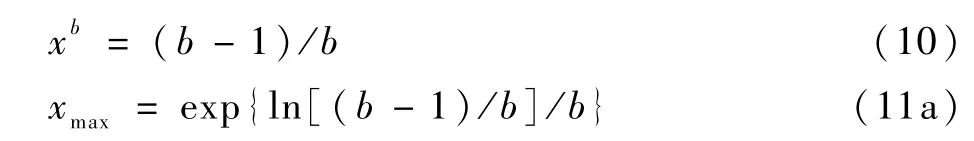
再求f(x）的二阶导数：

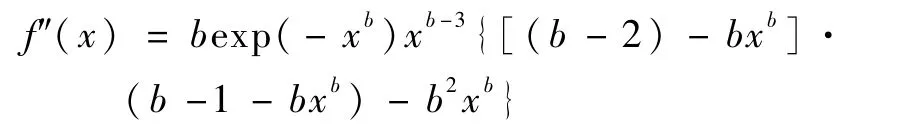
因f″(xmax）＝b exp(－xb）xb－3b(1－b）＜0，即证明了xmax为f(x）的极大值，且f(x）是凸函数。由式(11a）不难发现，当b越大时，ln［(b－1）／b］→0，xmax→1，峰值集中在x＝1处。

而对于两参数和三参数威布尔分布概率密度函数的极大值点位置分别为

4）威布尔分布的数学期望按照定义且设z＝xb可得

再注意到伽马函数的定义：

类似地，对于两参数和三参数威布尔分布的数学期望分别为

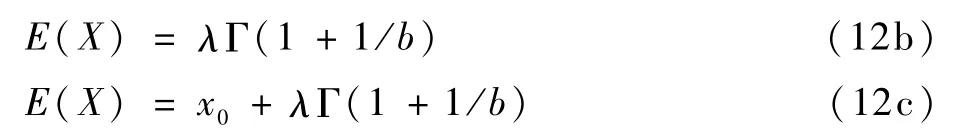
5）威布尔分布的方差。

同样按照定义可有

由式(13）可得

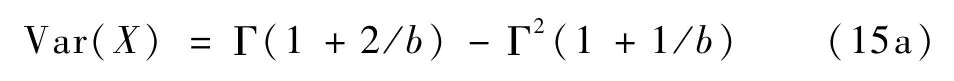
类似地，对于两参数和三参数威布尔分布的方差分别为

很明显，三参数的威布尔分布方差的期望值与x0没有直接关系。

6）关于威布尔分布和正态分布相似性的讨论。前面已提到当3＜b＜4时2种分布是相似的。正态分布意味着完全对称性，即均值、中值、峰值三者合一，而威布尔分布则不具备这个特点。不过在一定条件下，可让这3个值中的某2个值一致，如可令均值和中值相等，因此在这个意义上可认为与正态分布相似。均值可由式(12a）给出，而中值则可由式(9a）中P＝50%时给出，0.5＝exp(－），x50为50%可靠度的x值，可由式(12a）代替。

式(16）为超越方程，用Excel来解较麻烦。利用Python能很快得到结果。但不管哪一个方法都是利用牛顿二分法。为此可将式(16）改写为

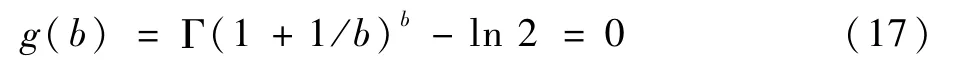
利用Excel可得b＝3.44(精确到10－5）。

Python中运行的结果为：k(对分次数）＝19，E(精度）＝1×10－8，b＝3.439 54。

Excel的优点在于直观，但在计算过程中需要人的介入，且效率较低。Python效率高，代码一旦调试成功，全部工作都可自动完成，精度也高。

顺便指出，这个结论虽然是从标准威布尔分布推出的，但对于两参数和三参数分布都是适用的，因对称性仅仅与形状参数b有关。另外按照文献［7］，威布尔分布的偏态系数为

不难看出，这个偏态系数也仅仅与b有关。同时，偏态系数为零时也应该是对称性最好的时候。亦是和正态分布最接近的时候，这对于比较这2种分布的异同意义重大，为此有必要求出这个b值。即要解如下方程：

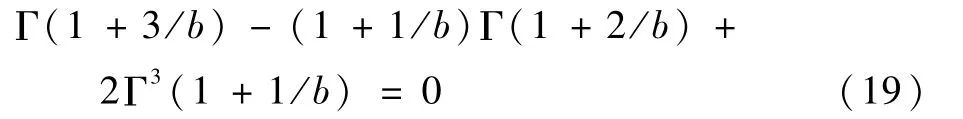
式(19）为一个关于b的超越方程，可利用相同Python代码得：k(对分次数）＝26，E(精度）＝1×10－8，b＝3.602 35。这与前文的b＝3.44比较接近，但并不重合，这也表明威布尔分布不可能完全对称。

3 疲劳统计学的智能化

20世纪80年代，计算机在中国刚刚开始起步和普及，做一些简单的统计工作没有问题，但在工程实践中应用较少。一方面是因为硬件不行，另外一方面懂得编程的工程技术人员不多。因此，各种现成的图表，如正态概率坐标纸、威布尔分布概率坐标纸等还是广为使用。这个方法虽然看起来比较简单实用，但误差较大，且必须将数据对数化，这从数学的角度看是一种空间变换，而这样一变换很可能会将这2种分布变得看起来不可区分。更加重要的是，这种方法难以将拟合程度量化。只能够看起来拟合不错，但实际上并非如此。所谓智能化，就是要将得到的数据直接通过计算机来得到人们要求的统计结果，即不仅是由计算机画出直观的图表，而且还有给出判断的定性与定量的结果。现举例说明。

例1取一组试件疲劳寿命如表1所示［1］。

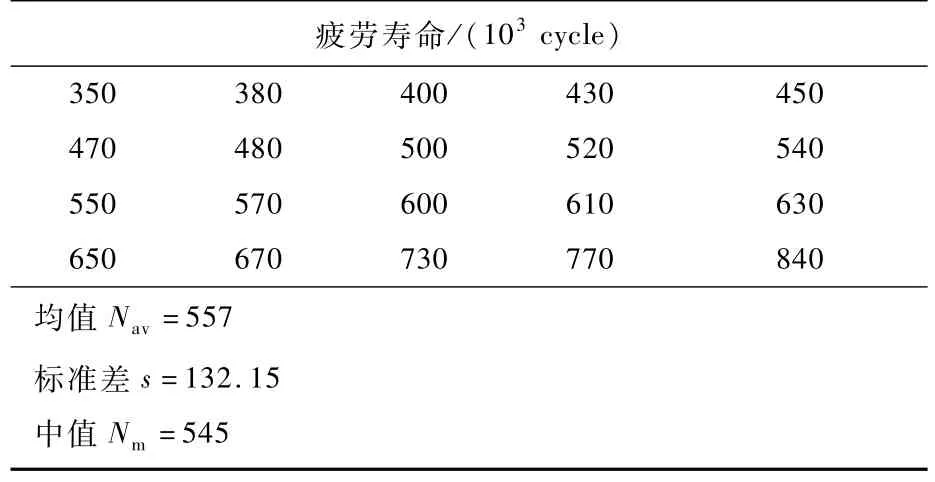
表1 一组疲劳寿命数据［1］Table 1 Aset of fatigue life data［1］

表1中：cycle表示循环次数，而均值Nav、标准差s及中值Nm皆由Excel得出。若这些数据是服从正态分布的，则相应的正态分布参数的估计值可由式(20）给出：

式中：“＾”表示估计值。

于是，相应的正态分布密度函数为

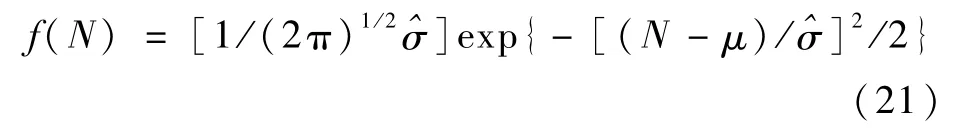
现若假定它们服从三参数威布尔分布，则求其3个参数，由式(9c）、式(12b）及式(15c）分别得到

式中：N0为估计安全寿命；Na为估计特征寿命。

从式(24）得

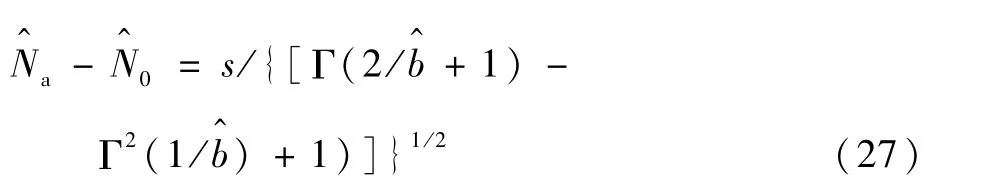
再由式(23）得

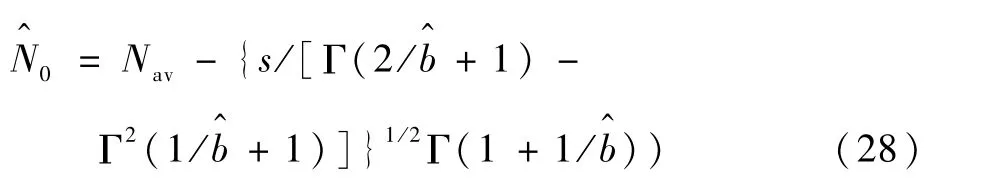
再将式(26）～式(28）代入式(22）可得

由以上参数和式(1a）得出相应的威布尔分布概率密度函数如下：

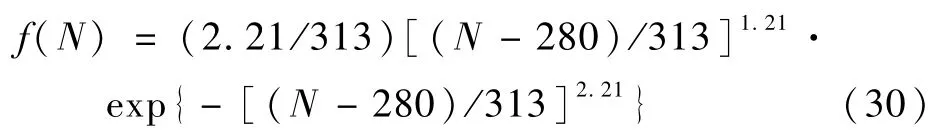
利用Excel，将由该数据得到的正态分布式(22）和威布尔分布式(30）的可靠度在图2中做一个比较。

但从图2中很难回答哪一个分布的可靠度估计更好一些。为此考虑到可靠度估计值［8-9］(也可参考文献［1］）：

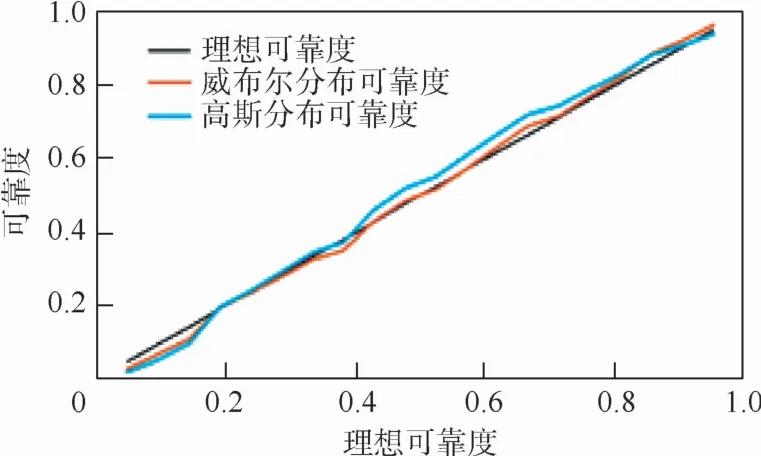
图2 正态和威布尔分布可靠度比较(例1）Fig.2 Comparison of normal and Weibull distribution reliability(Example 1）

式中：i为数据(观测值）由小到大排列的序数；n为数据的个数。

不过仍然可从另外一个角度来看正态分布是否被满足，即卡方检验，但此法相当麻烦，可参考文献［1］。

例2利用文献［1］表12-3中的数据绘制表2。

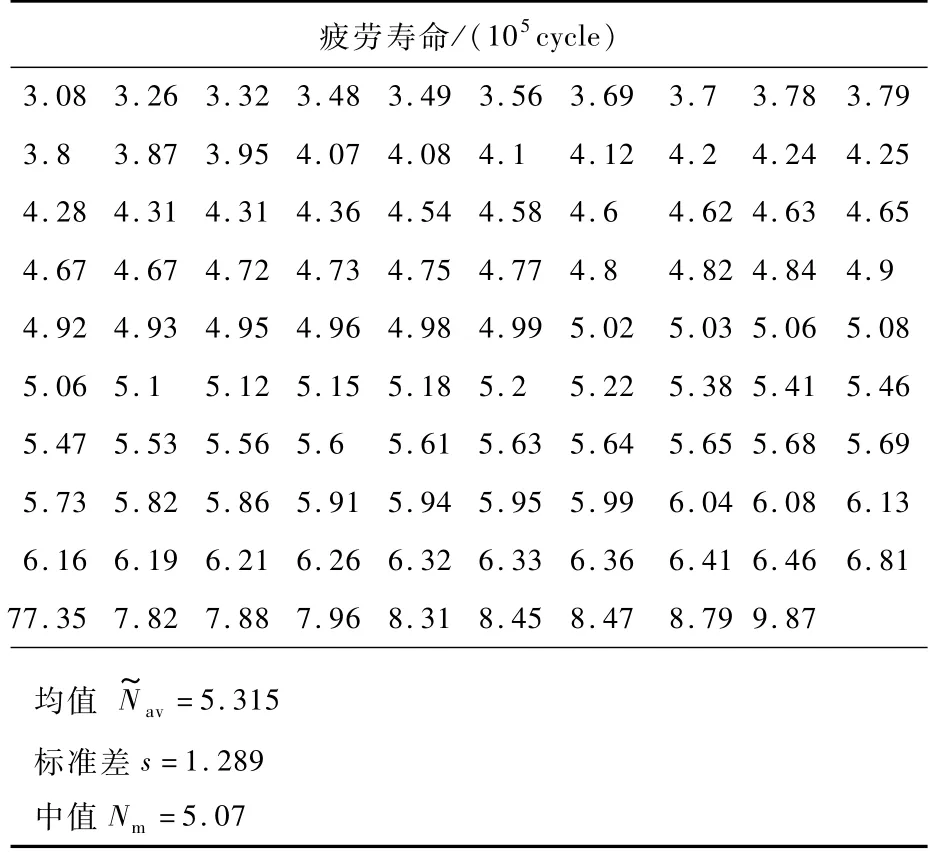
表2 100个试件在同一应力条件下疲劳寿命数据Table 2 Fatigue life data of 100 specimens under the same stress condition

对于例2，仍然可和例1一样画出正态分布和威布尔分布的可靠度拟合图，以及给出两者对于理想可靠度的决定系数［6］。不过，因为数据较多，采用Excel很困难，但用Python处理较容易。Python代码运行结果为：Nav＝5.315，s＝1.289，Nm＝5.07，Cs＝1.021，k(对分次数）＝20，E(精度）＝1×10－7，b＝1.526，N0＝3.39，Na＝5.53(102cycle）。

验算：Nav1＝5.315，s＝1.289，Nm1＝5.07，正态分布与理想可靠度的决定系数为0.979 14，威布尔分布与理想可靠度的决定系数为0.988 44。

在此要注意这里用的是决定系数［10］而不是相关系数来区分拟合水平，主要是因为图3的横坐标变成了疲劳寿命，这样其与可靠度的关系不再是线性关系。计算结果表明，威布尔分布的决定系数仍然比正态分布大，尽管不是大很多。最重要的是，这些数据是偏态的，用正态分布已经不能很好描述。而威布尔分布恰恰弥补了这个不足，如图3所示。不过，也必须指出用这个解析法来求威布尔分布的3个参数并非没有瑕疵。例如，经过计算，若这些数据满足威布尔分布，那么安全寿命是3.39，但开始3个数据是小于这个值的，则计算过程没有问题，很可能是因为这个方法先将形状参数b找出来后再计算N0和Na，就无法保证N0一定会小于输入的数据的最小值。故需要对威布尔分布参数算法做进一步的研究。

图3 正态和威布尔分布可靠度比较(例2）Fig.3 Comparison of reliability between Normal and Weibull distribution(Example 2）

4 高镇同法

第3节指出计算威布尔分布的解析算法还存在一些问题，如计算出来的安全寿命比实际的数据还要大，说明了这个算法是不自冾的。这里存在2种可能性：一是这些数据并不那么符合威布尔分布；二是上述计算威布尔参数的算法还存在问题，即用样本估计的均值和方差值来代替总体相应的均值和方差存在较大误差。为此，可从另外一个角度来计算这些参数，如用最小二乘法。为简单，从二参数的威布尔分布开始，由式(9c）可有

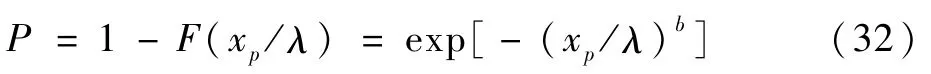
其估计值可利用式(31），式(32）在取二次自然对数后可得

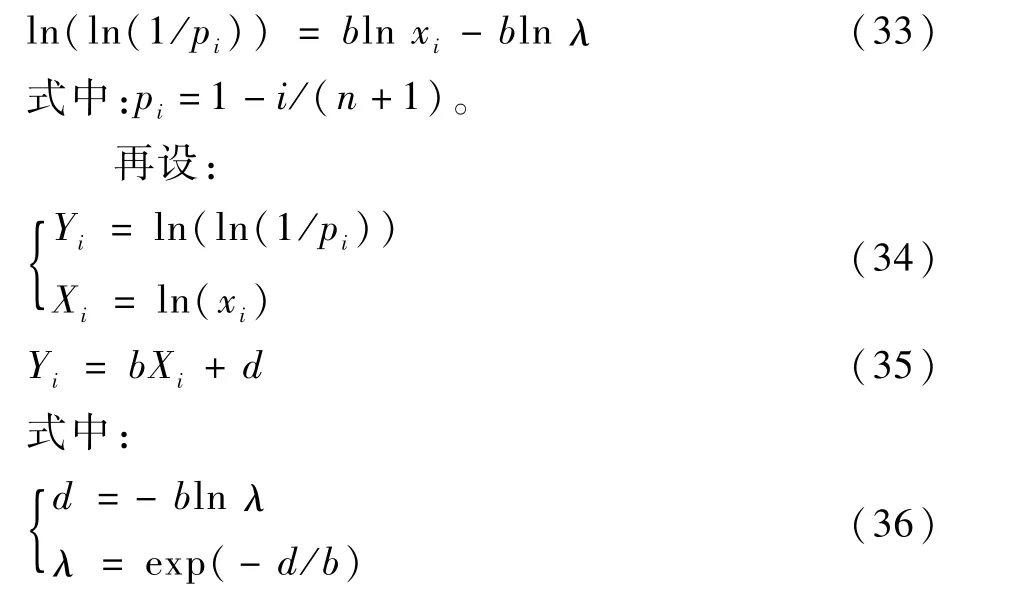
于是，可通过最小二乘法来求出b、d及λ。但问题并非那么简单，因为用二参数威布尔分布的前提是设位置参数或安全寿命x0＝0。在实际情况下，x0≠0，而且恰恰是因为这个x0≠0才显示出威布尔分布的优越性。事实上，系数b和λ及相应的相关系数r都是x0的函数，可通过解析法来求出使得相关系数r的极大值，但这种方法推导较麻烦，容易出错。用Python在0≤x0＜xmin区间中(这里的xmin就取给定数据的最小值）可直接将r关于x0的图画出来，如图4所示。然后用Python智能地将相关系数最大的r的x0找出来。理论上分为两步，但在实际编的代码中是一气呵成的，即以x0为变量，找出r的极大值同时将b和λ确定，这就是高镇同法。具体表述如下：

图4 安全寿命与相关系数的关系(例3）Fig.4 Safety life versus correlation coefficient(Example 3）

1）输入原始数据，若原始数据没有排好序，则先排序。

2）利用Python中的scipy可直接通过以给定精度的间隔来遍历x0的可能值区间［0，xmin］，以求出使得相关系数最大的x0，即x0max。

3）注意到，在scipy中计算相关系数时，事实上是先求出最小二乘法中直线方程的相应系数b和d，推出λ＝exp(－d／b）。因此一旦定出了x0max，则威布尔分布相应的参数b与λ也就同时得到了。

例3现利用例1的数据在Python代码上进行试算，可得到如下结果：N＝｛350，380，400，430，450，470，480，500，520，540，550，570，600，610，630，650，670，730，770，840｝，Nav＝557.0，s＝132.152，Nm＝545.0，Cs＝0.408，r＝0.999 218，bm＝2.040，λ＝320.98，N0＝276.60，Cs＝0.605，Nav1＝560.97，s＝146.04，Nm1＝544.79，解析法威布尔分布与理想可靠度的相关系数为0.999 20，高镇同法威布尔分布与理想可靠度的相关系数为0.999 22。

例4高镇同法与解析法最大不同是b值不同(前者b＝2.21，这里b＝2.040，相差8%），从而标准差s不同(132 vs 146，相差10%）。但相关系数r(0.999 20 vs 0.999 22）只有10－5，在这个意义上两者并没有什么大的差别。因解析法对例2的解是不自冾的，对Python的代码稍加修改可得如下结果：Nav＝5.32，s＝1.29，Nm＝5.07，km＝2 780，r＝0.993 763，bm＝2.147，λ＝2.87，N0＝2.780，Nav1＝5.32；s1＝1.25，Nm1＝5.20，正态分布与理想可靠度的决定系数为0.979 11，威布尔分布与理想可靠度的决定系数为0.989 03。

图5形象地给出了例4中的数据如何使用高镇同法。先求出相关系数和安全寿命N0的关系曲线，再找出使得相关系数最大的安全寿命。

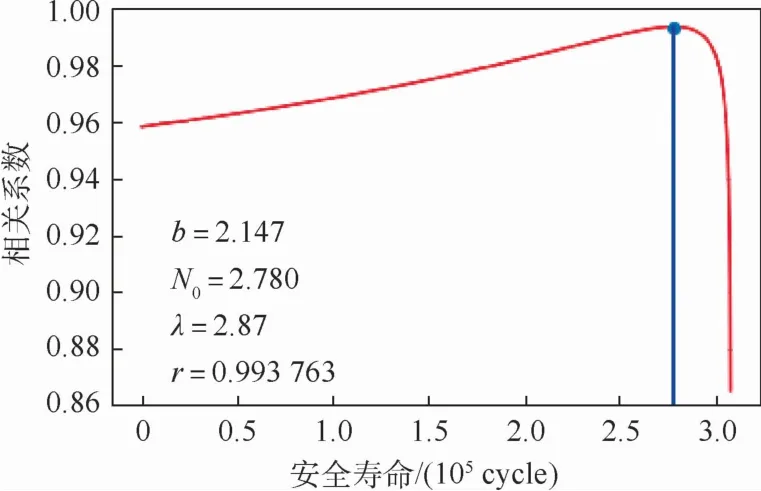
图5 安全寿命与相关系数的关系(例4）Fig.5 Safety life versus correlation coefficient(Example 4）

由此可见，高镇同法的结果与前面的解析法明显不同，即不存在超过安全寿命N0的原始数据。几个参数都较符合，即使是标准差也只有3%的误差，且高镇同法得到的相关系数明显大于解析法。在此意义上，可认为高镇同法是优于解析法的。

例5值得注意的是，高镇同法与文献［11］中提出的“确定威布尔分布三参数相关系数优化法”还是有所不同的，主要体现在：文献［11］中的数学推导较麻烦，相应的代码也会较复杂，仍然没有充分发挥出利用计算机智能的优势。将文献［11］中表3的数据放入同样的Python代码即得如下结果：N＝｛325，376.3，387.3，447.5，456.3，524.3，574.4，635.1｝，Nav＝465.77，s＝105.763，Nm＝451.9，Cs＝0.302，r＝0.992 976，bm＝1.747，λ＝250.00，N0＝251.84，Cs＝0.823，Nav1＝474.52，s1＝131.51，Nm1＝454.54。

图6给出了例5如何使用高镇同法(参照文献［11］中的表3数据绘制图6）。而得到的结果与文献［11］中的结果几乎一样，但要注意在文献［11］中得到的相关系数是负的，而这里是正的，主要是因为在文献［11］中设Y＝－ln［ln(1／p）］。

图6 安全寿命与相关系数的关系(文献［11］中的表3）Fig.6 Safety life versus correlation coefficient(Table 3 of Ref.［11］）

由此可见，本文方法相对简单，容易掌握，不会出现矛盾的结果。这表明高镇同法具有相当的优越性，值得推广。

5 高镇同法的应用

高镇同法对于拟合三参数疲劳性能曲线也是可以应用的。因为这与求威布尔分布的三参数在数学上是没有区别的。即用相关系数最大化来定出位置的同时，再由最小二乘法求另2个参数，即可智能化地同时得到3个参数。

例6文献［7］中给出了一个三参数幂函数表达式：

式中：S0、m和C为材料常数；Smax为最大应力。

文献［7］虽然也是用最小二乘法，利用相关系数最大化来求出S0，再去求另外2个参数，但较麻烦。现介绍高镇同法如何用应在例6中。设S0为已知，在式(37）两边取10为底的对数：

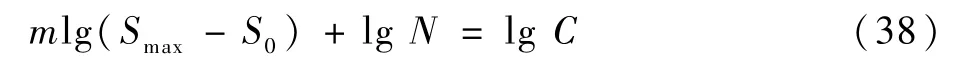
再设：Y ＝lg(Smax－S0），X ＝lg N。

即可得

按照高镇同法，可将S0根据需要而定的精度遍历区间［0，Smax］，以求出使得相关系数最大的S0，同时得出相应的b和d，再由式(39）定出m和C。结果与文献［7］几乎相同。以文献［7］第11章例4中的数据为例，绘制表3。

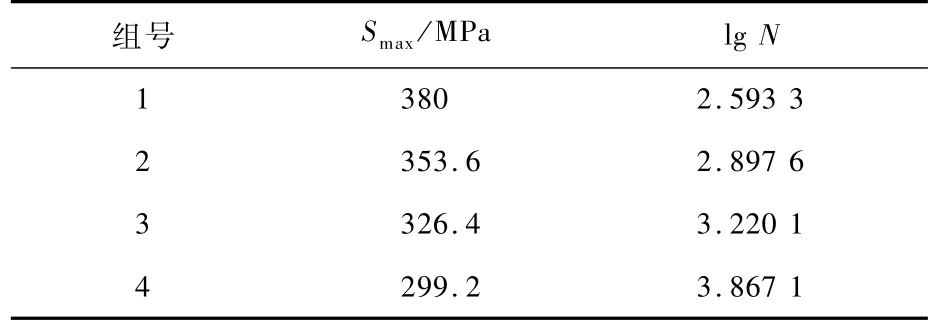
表3 例6的一组数据Table 3 Exam ple 6 aset of data

其Python代码与高镇同法类似(要注意此时相关系数是负的），可得如下结果：km＝27 089，r＝－0.999 14，S0＝270.89，m ＝2.146，C＝9.599 4×106。

由图7可知，高镇同法得到的曲线与实际值拟合得很好。图中：S0＝270.89，m＝2.146 4，C＝9.599×106，r＝－0.999 14。其结果和文献［7］的结果：r＝－0.999 1，S0＝270.89，m＝2.142 5，C＝9.444 5×106，除了C相差比较大一点(不超过1.7%），其他参数的相对误差都不到10－3。但用高镇同法计算较方便。

图7 S-N拟合曲线Fig.7 S-Ncurve fiting

例7以文献［7］中第11章例5中的数据为例，绘制表4。

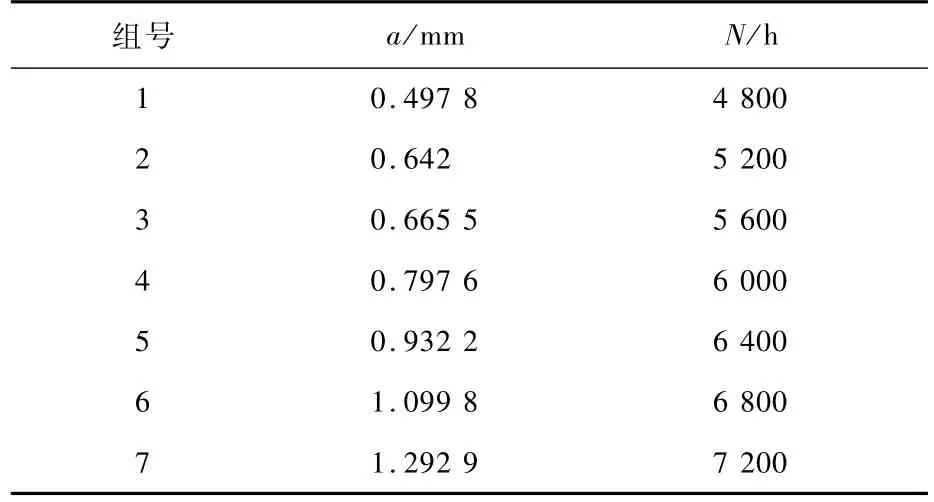
表4 例7的一组数据Table 4 Example 7 aset of data

表4中数据服从如下经验公式：

式中：a为试件出现裂缝的长度；C、m、a0(也称为初始裂缝长度）都是与材料有关的常数。

很明显，式(41）与式(37）是不一样的，物理意义更加不同。取对数后：

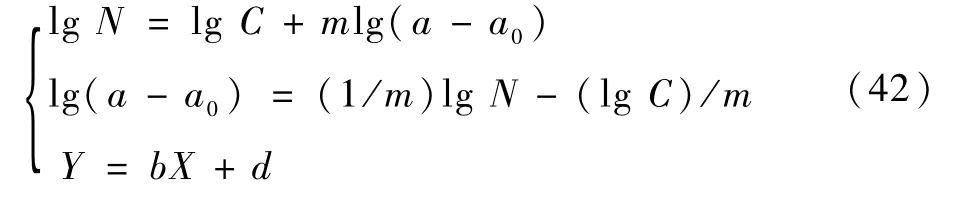
式中：Y＝lg(a－a0），X＝lg N。

同样用高镇同法，以视需要而定的精度使a0遍历区间［0，amin］，可求出使得相关系数r最大的a0。再根据式(43）定出C和m。将Python的代码做出适当的修改可得如下结果：r＝0.992 03，a0＝0.173，m＝0.343，C＝6.989 6×103。

图8表明，由高镇同法计算出来的结果与实际值拟合相当好。图中：a0＝0.173，m＝0.343 10，C＝6.989 6×103，r＝0.992 03。其结果与文献［7］的结果：r＝0.992 0，a0＝0.176，m ＝0.336 5，C＝6 976相差非常小。就相关系数而言，其差别可以忽略不计，如果仅从图形上看，两者也难以得出有多大差别。而对于其他系数，相对误差都不超过2%。即相关系数10－4的差异可能会引起拟合曲线各参数的差异扩大上百倍。这个结论也符合三参数威布尔分布，与取对数后的线性化是有关的。

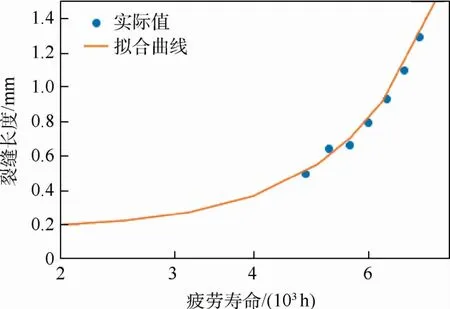
图8 a-N拟合曲线Fig.8 a-N curve fitting

最后，要对高镇同法的由来再做一个简要的说明。①高镇同法的基础严格来讲应该是最优拟合，最小二乘法只是其特例。在文献［11］中已给出了一些很好的例子。②在文献［11］的基础上，不少学者［12-15］都做了不少改进工作，取得了一定的成绩，特别是回看文献［15］离高镇同法只有一步之遥，很可惜没有再深入下去。③为了解决解析法出现的不自冾问题，不通过直接求相关系数极大值，而是利用scipy这个软件库将所有可能的相关系数求出来之后通过排序将最大值求出来，同时也将相应的威布尔参数求了出来。且从数学角度看此法对于负的相关系数也是同样适用的，很快就能推广到三参数疲劳性能曲线的拟合中使用。

6 结论

1）威布尔分布是一种全态分布，比正态分布更具有一般性，可以相信在大数据时代将发挥出更大的作用。特别是应用到疲劳统计学中具有100%可靠度的安全寿命，简称为安全寿命这个参数，其涉及可靠性的实际应用领域中具有重大意义。

2）将疲劳统计学智能化的一个重要切入点是将估计威布尔分布三参数智能化。威布尔分布的数学形式虽然比较复杂，但完全可用像高镇同法(充分利用Python的特点而创造出来的一种新算法）智能化地克服图解法和解析法的弱点，很方便地解决威布尔分布三参数的计算问题，不仅如此，同时可解决广义三参数疲劳性能曲线的拟合问题。

3）疲劳统计学智能化不仅是实际应用中必不可少的一个工具，在理论研究中也是功不可没。例如，如何确定威布尔分布的无偏性和对称性，若没有计算机智能的帮助其计算复杂性也是令人却步的。

4）本文提倡的疲劳统计学中的智能化主要是指：①不再需要各种各样的有关统计函数值的表，都可通过计算机得到；②所有的数据处理和图表都可由计算机自动完成；③只要给出(疲劳寿命）样本数据通过计算机就可判断该数据的总体服从的最佳分布(正态分布或威布尔分布），并同时给出该分布的参数。特别是高镇同法可使得威布尔分布的应用更加方便，对于其普及具有重大意义。

当然上面说的智能化还是处于初级阶段，这里有两层意思：一是疲劳统计学的智能化水平本身还不够高，二是使用的人还不够广泛，尽管Python已经非常容易学习和使用。随着计算机在疲劳统计学中的使用越益广泛和深入，可以相信达到比较成熟的智能化阶段并非遥不可及。

致谢感谢力中国际融资租赁有限公司万伟浩先生对于本文及有关研究工作的支持。