钢筋混凝土框架柱延性破坏准则研究
2021-11-17刘伯权
付 国,何 斌,刘伯权
(1. 西北农林科技大学水利与建筑工程学院,杨凌 712100;2. 长安大学建筑工程学院,西安 710061)
钢筋混凝土柱是框架结构的主要承重构件,研究其抗震性能量化方法对提升结构整体性能、实现大震不倒设防目标、防止过早发生倒塌破坏具有重要意义。建立便于工程应用、符合性能退化规律和破坏现象的破坏准则,一直是抗震研究领域的热点内容。近年来研究人员不断完善与发展现有破坏准则,以提升破坏准则的适用范围和精确度,取得了大量研究成果[1-6]。基于性能的抗震设计方法已经被工程界所认可,通过大量震害调查和试验研究,细化了不同类型结构的变形量化限值[7],变形准则、能量准则、Park-Ang 双参数准则是破坏准则研究的主要方向和内容。
变形准则具有定义明确、测量方便的特性,且经受了大量的试验验证,我国抗震规范定义的位移角限值1/50 是留有足够安全储备的[8],其本质上是结构不倒塌的标准而非倒塌标准。能量准则通过对比地震动输入能量和结构所能提供能量大小,可较好地定义构件破坏,但耗能划分和计算仍是研究的重点和难点问题。Park-Ang 双参数准则[9-10]选取变形和耗能的组合定义柱的破坏,反映了首超破坏和累积损伤的影响,变形、耗能对结构破坏的贡献大小及耦合作用仍需大量深入的量化研究。刘伯权[11]研究了等位移幅值加载下混凝土柱的低周疲劳特性,提出了等效延性破坏准则,但在准则应用和计算精度上仍需更多研究。
本文研究钢筋混凝土柱破坏现象、承载力退化和延性变化规律,考虑变形能力强弱对柱破坏的影响,提出一种改进的延性破坏准则。对柱低周反复加载和单调加载试验数据进行分析,考查延性破坏准则对构件破坏评估的有效性。
1 破坏准则概述
破坏准则应从宏观现象、承载力退化、变形增长、滞回耗能等方面解释性能退化规律和破坏机理,破坏指数计算需考虑变形、荷载、耗能等性能指标的影响,还应考虑加载制度、设计参数等因素的影响,同时兼具计算简便、破坏标准合理等特性。
1.1 变形准则
变形准则定义结构破坏为变形值超过某一临界状态,具有概念清晰、判定标准唯一的优点,适用于单调、低周反复、地震动等加载方式。

混凝土柱变形能力的影响因素包括:1)配筋率、配箍率、混凝土强度等设计参数等;2)试验方案中位移加载幅值、加载顺序、轴压比等;3)破坏过程中裂缝发育、保护层剥落、核心区破碎、纵筋箍筋失效类型等。不同混凝土柱的延性大小存在较大的差异,单一破坏标准很难反映构件破坏的差异性,甚至高估构件的变形能力和安全储备。
针对美国太平洋地震中心(PEER)混凝土柱数据库[12]的88 组矩形截面柱试验数据进行分析,重点研究峰值点(对应最大荷载)和极限点(对应最大变形)的位移角变化规律。
图1 是峰值点和极限点位移角的对比图,绝大多数柱破坏时位移角超过了1/50 限值且留有一定安全储备,但安全储备的多少具有显著差异。由图2 中位移角限值与极限点、峰值点对比曲线可知,两者没有特定比例关系且多次相交,说明位移角为1/50 时,承载力退化、变形程度与构件最终破坏缺乏比例关系。单一位移角限值不能合理定义性能退化规律与程度,很难在兼顾安全与经济的基础上判定混凝土柱的破坏。

图1 峰值点与极限点位移角对比Fig. 1 Comparison of displacement angle between maximum load and maximum deformation
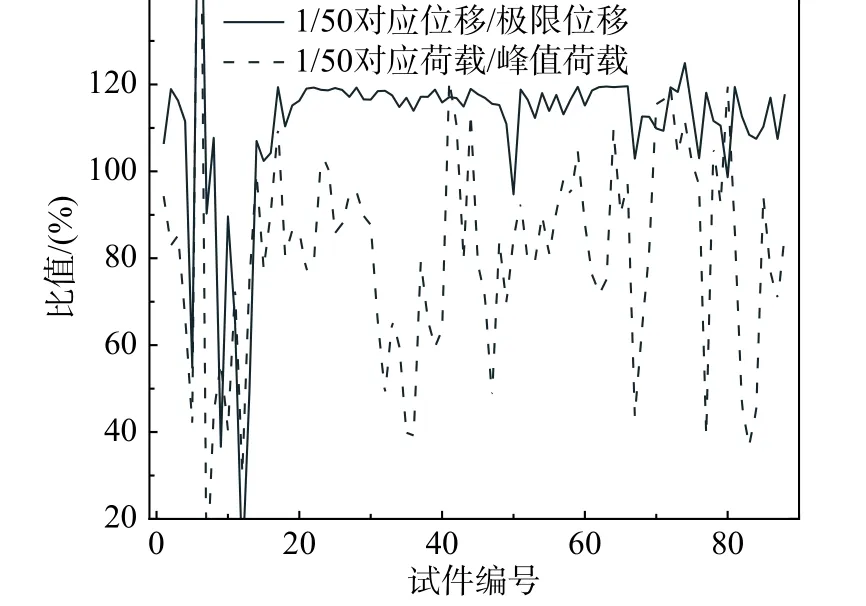
图2 1/50 位移角对应的变形与荷载曲线Fig. 2 Relationships between ultimate load and deformation of 1/50
图3 是峰值点变形与极限点变形、极限点荷载与峰值点荷载的比例关系图,混凝土柱的变形、荷载变化存在较大的差异,选择变形、承载力退化或两者组合的方式定义构件破坏仍有待深入开展。
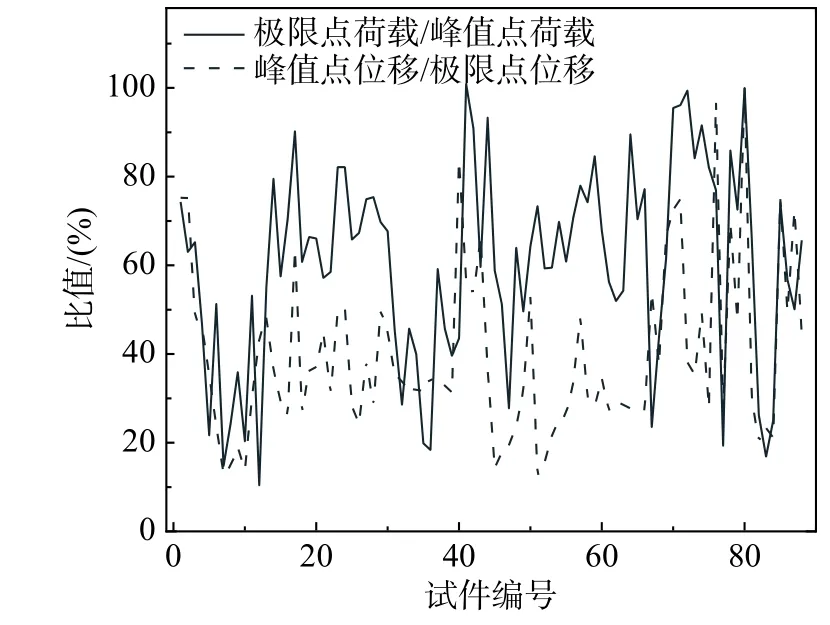
图3 承载力和变形的退化曲线Fig. 3 Degradation curve of load and deformation
1.2 能量准则
结构地震响应是一个能量输入和耗散的过程,能量准则在理论上最为合理,由于混凝土保护层开裂、纵筋屈服、保护层初始剥落、混凝土保护层完全剥落、箍筋拉断、纵筋屈曲和纵筋拉断等破坏过程中的不确定性,破坏对应总能量的统计和分类工作复杂且不易确定[7]。
不同加载幅值和加载制度使得构件破坏和对应滞回耗能也存在较大差异,刘伯权[11]完成了相同设计参数的20 个框架柱拟静力试验,由表1 可知不同加载幅值和加载顺序下构件破坏所需滞回耗能存在显著差异甚至相差数十倍。随加载幅值的增加单周滞回耗能值迅速增加,但构件破坏所需的总滞回耗能值却显著下降。

表1 钢筋混凝土柱低周疲劳试验参数[11]Table 1 Low-cycle fatigue experiment of RC columns
将能量划分为弹性变形能、塑性变形能和损伤耗散能量三部分能够更好定义破坏[13],其中损伤耗能的累积最终引起结构破坏,确定各部分能量所占比例大小是破坏准则研究的重点和难点。文献[14 - 16]探索了能量划分的方法和依据:1)直接引起结构或构件破坏的部分耗能为有效耗能;2)其余能量不引起破坏或延缓破坏,如核心区已压碎混凝土的研磨等,能量划分方法、合理性验证仍是后续研究的关键。
1.3 Park-Ang 双参数准则
Park-Ang 双参数破坏准则[9]定义结构破坏是由最大变形和累积耗能共同作用引起的。

Park-Ang 准则较好地考虑了首超破坏和累积耗能的影响,且破坏指数计算值与试验结果吻合较好,其中组合参数β 和倒塌指数不为1 等是后续研究的主要方向[17-20]。
考虑变形增减与耗能增减之间的耦合关系,由剪跨比、轴压比、纵筋配筋率、体积配箍率等参数组合得到的β 能否从理论上解释变形与耗能对破坏的影响规律仍需深入研究。根据不同加载幅值的构件耗能特性引入有效耗能假设,改进的Park-Ang 准则可更好的定义结构破坏,耗能计算是影响破坏指数准确性的重要参数[14]。以表1 的2 组对比试验为例(CF-12/CF-13、CF-14/CF-15),同位移幅值加载下单周滞后耗能基本相同,总耗能大小甚至相差十余倍,考虑耗能的巨大差异与柱破坏之间关系仍需开展广泛的试验研究和数据验算。
1.4 等效延性破坏准则
刘伯权[11]研究了框架柱的低周疲劳特性,提出包含延性大小和加载次数的等效延性破坏准则。


1)延性系数是柱塑性变形发育程度的量化指标,既反映变形的大小,也定义塑性变形发育程度的大小,较位移更适宜预测和评估构件破坏。
2)加载次数与加载幅值的组合反映了构件破坏的累积效应,加载次数越多、加载幅值越大,柱的破坏越严重。
3)延性准则适用于单调加载、低周反复加载、地震动加载三种不同的加载方式,实现了破坏准则形式上的统一。
2 延性破坏准则
2.1 延性准则计算式
根据已有试验研究资料,对混凝土柱的部分破坏特性总结如下:
1)考虑地震动作用的时间相对较短且往复次数有限,混凝土柱位移加载幅值低于屈服位移时,构件几乎不发生破坏,定义弹性范围内即延性系数μ<1 时柱不破坏,对应破坏指数为0。
2)单调、低周反复等加载方式下单调加载位移值最大,可取单调加载下的混凝土柱极限位移为柱的最大延性系数μmax。μmax考虑了轴压比、剪跨比、配筋率、混凝土强度等设计参数。
单调加载下柱的极限位移可由式(7)和式(8)计算得出[21]:


3)低周反复加载过程中位移幅值、加载次数对构件破坏的影响最为显著,是破坏准则中必须包含的参数。抗震理论和试验研究表明轴压比和配箍率对构件破坏和性能退化有显著影响。
综上,通过试件的试验数据计算研究,定义框架柱的延性破坏准则如下式所示:

2.2 参数定义与说明
小于屈服位移时 (μi-1)项为0,表示延性系数小于1 时柱不发生性能退化,随着延性增加构件破坏程度也进一步加剧。延性系数项取2,主要基于改进Park-Ang 准则研究和耗能计算中揭示的耗能与延性系数存在近似平方关系[14]:1)破坏指数增加与延性增加是非线性的;2)变形与承载力存在对应关系,参考耗能计算方法定义延性系数与破坏指数为平方关系,延性准则计算结果也表明平方关系能够较准确的定义混凝土柱破坏。
βi为相同位移加载幅值的循环次数,当循环次数小于3 时取实际循环数,循环次数大于3 时取βi=3。
轴压比影响系数kn解释了随轴压比增加构件破坏程度加剧的试验现象,22n关系式由破坏指数计算数据拟合得出。前期拟合数据均为轴压比0.2 的试件,系数取0.3 考虑n=0.2 时kn=1.019 ≈1.0。
配箍率影响系数kρv借鉴阿伦尼乌斯公式进行研究,由于混凝土柱低周反复加载试验中直接研究配箍率影响规律的试验较少,延性准则首先完成kρv=1.0 的计算研究。
需要指出的是μmax与kn计算式中均包含了轴压比系数,μmax是混凝土柱在单调加载下的理论最大变形能力,与低周反复试验无关;而kn是反复加载试验过程中延性系数与柱破坏程度之间关系的系数,两次轴压比计算的适用范围和目的不同。
3 延性破坏准则验证
3.1 低周反复加载试验验证
为验证延性破坏准则的合理性和准确性,首先对比了Park-Ang 准则[22]、改进Park-Ang 准则[14]与延性破坏准则的计算结果,并将全部加载循环对应的破坏指数进行对比,计算结果如表2 所示。

表2 破坏指数计算对比Table 2 Comparison of damage index
三种破坏准则对应的破坏指数平均值分别为1.408、1.084 和0.857,延性准则对应破坏指数最小,限于篇幅选取了试件Kzc4 和Kzb3,将Park-Ang 准则、改进Park-Ang 准则、延性准则计算结果分别绘成柱状图,如图4 所示。
由图4 可知延性系数为1 时,延性准则对应破坏指数为0,表明结构弹性阶段几乎不发生破坏;延性系数较小时,延性准则破坏指数显著小于Park准则和改进Park 准则,小位移幅值加载下结构破坏程度轻微,与试验现象更为吻合;接近破坏时延性准则对应破坏指数增加迅速,更好地解释了位移加载幅值越大破坏程度越严重的试验现象。
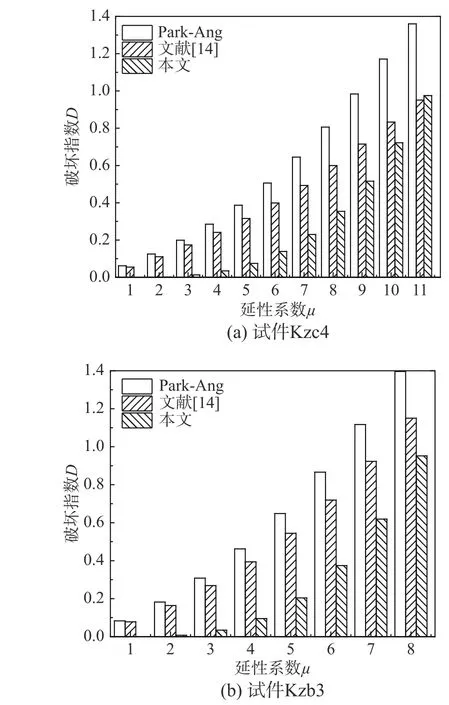
图4 三种准则对应的破坏指数对比Fig. 4 Comparison of damage index base on three failure criterion
为验证延性准则的合理性与准确性,选取日本Kawashima[23]数据库部分混凝土柱以及国内混凝土柱试验数据进行了计算和验证,由于数据较多,所有试验的详细参数不详细列出,文献来源和编号见表3,计算结果见图5。

图5 混凝土柱反复加载破坏指数Fig. 5 Damage index of RC columns under cyclic loading

表3 混凝土柱试件文献来源与编号Table 3 Literature sources and numbering of RC columns
105 组框架柱的破坏指数平均值为0.923,标准差为0.265,延性准则能够很好地预测构件破坏。离散性偏大的一个主要原因是承载力退化大小不统一,以文献[24]为例(破坏指数见图6),承载力退化至85%时破坏指数平均值为0.655,退化至40%为1.406,两者相差超过1 倍。

图6 承载力退化至85%与40%时的破坏指数Fig. 6 Damage index of capacity degradation with 85% and 40%
根据各试件的承载力退化值,将已完成的105 组数据按照承载力退化程度重新进行了排序(承载力退化值优先由文献得出,未明确给出的由滞回曲线得出),得到退化程度为20%~30%、30%~40%、40%~50%、50%~60%、60%~70%、70%~80%、80%~90%共7 组破坏指数平均值,如图7 实线所示。
对90%分组数据进行整理,李义柱[29]、刘金升[30]、钱稼茹[31]组试件按滞回曲线得到的承载力退化幅值分别为54.7%、37.0%、72.6%、60.6%、78.6%(数 据 由GetData 软 件 描 点 得 出),TP-15、TP-16 较TP-14 加[23]密区分别增长1 倍和2 倍,解咏平[26]组研究了构件的尺寸效应,对应2 组数据的加载循环数多,移除以上数据后90%分组包含了5 组试件,对应破坏指数平均值为0.631,调整后见图7 虚线。钢筋混凝土柱的承载力退化越严重,破坏指数越大,破坏程度越充分。

图7 破坏指数与承载力退化关系图Fig. 7 Relationship curves of capacity degradation and damage index
3.2 单调加载试验验证
把单调加载视为位移幅值为 Δmax、加载循环数为1/4 的滞回加载[11],单调加载下(μi=μmax)的延性破坏准则计算式可改写为:

延性破坏准则将两种加载方式对应的破坏指数计算统一到一个公式中,同时考虑了首超破坏和累积损伤破坏,反映了位移幅值和滞回循环对构件破坏的影响,对文献[11, 25, 41]的单调加载试验数据进行了分析,得到破坏指数如图8 所示。
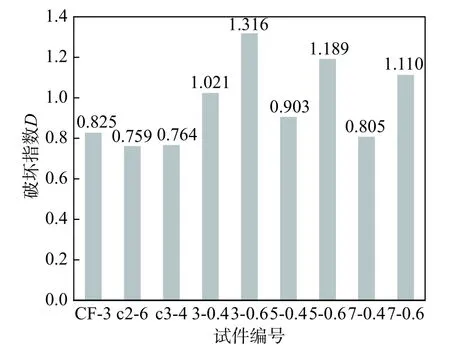
图8 钢筋混凝土柱单调加载破坏指数Fig. 8 Damage index of RC columns under monotonic loading
单调加载试验破坏指数计算结果表明,9 组试件的平均值为0.966,标准差0.191,延性准则也可以较好地定义混凝土的首超破坏,解释单调加载下构件的破坏规律。
4 考虑配箍率变化的延性破坏准则
4.1 配箍率影响系数
箍筋对增强核心区混凝土约束、抗震性能提升具有显著影响,收集到的试验数据中直接研究配箍率与破坏规律的数据较少,需要借鉴相关理论探索配箍率对构件破坏的影响。
阿伦尼乌斯公式是由瑞典的阿伦尼乌斯所创立的化学反应速率常数随温度变化关系的经验公式:

式中:k为速率常数;R为摩尔气体常量;T为热力学温度;Ea为表观活化能;A为指前因子。研究表明阿伦尼乌斯公式计算值与试验值吻合较好,在化学反应速率方面获得了广泛应用[42-43]。
如果把混凝土柱的破坏类比为化学反应,配箍率类比为温度,混凝土柱的破坏过程也可用阿伦尼乌斯公式进行说明。常数Ea对应配箍率对构件性能提升的最小值, 1/ρv表明配箍率较低时ρv增加对柱的性能提升影响显著,随着配箍率增加对构件破坏的影响趋缓。
为降低试验和文献来源的误差,将105 组数据按配箍率每隔0.1%划分一组,包括0.5%~0.6%、0.6%~0.7%、···、2.2%~2.3%、2.3%~2.4%共15 组数据,删除了数量过少或破坏指数显著偏大的3 组数据,每组取平均值后得到散点图如图9所示。

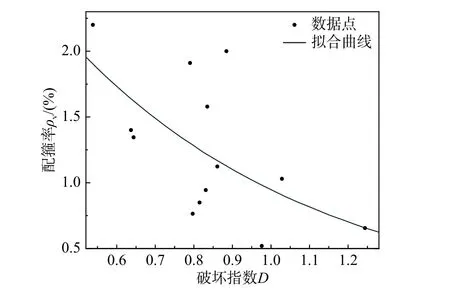
图9 kρv 拟合曲线Fig.9Curvefittingof kρv


图10 不同配箍率的混凝土柱破坏指数Fig. 10 The columns damage index in different stirrup ratio
4.2 改进后的延性准则计算研究
由于混凝土材料、加载制度、设计参数的差异性,且缺少柱破坏临界状态的统一标准,为说明改进后延性准则公式合理性,本文定义破坏指数随承载力退化值线性减少,即:
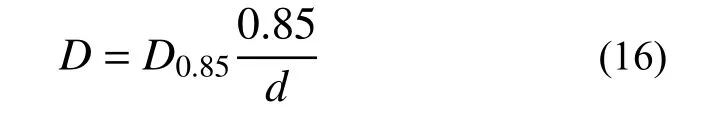
式中:D0.85为承载力退化至峰值承载力85%时结构的破坏指数;d为承载力退化值。
D0组破坏指数和Dρv组破坏指数根据承载力退化程度调整为85%后分别对应为D0,0.85组数据和Dρv,0.85组数据,两组破坏指数分布如图11 所示,四组破坏指数的平均值和标准差见表4。

表4 框架柱反复加载试验破坏指数Table 4 Statistical table of damage index under cyclic loading

图11 不同承载力退化程度的混凝土柱破坏指数Fig. 11 The columns damage index in different capacity degradation
D0组和Dρv组数据对比表明考虑配箍率影响后破坏指数平均值增大,但标准差增长较小,Dρv组数据能够更好揭示构件破坏特性。D0,0.85组数据与D0组数据的平均值和标准差变化均较小,Dρv,0.85组数据考虑了承载力退化和配箍率影响,破坏指数的平均值最接近1.0,且标准差变化不大。
4.3 改进后的单调加载延性准则计算研究
类似的将9 组单调加载试验对应的延性准则破坏指数也按四种情况分析,计算结果见表5。

表5 框架柱单调加载试验破坏指数Table 5 Statistical table of damage index under monotonic loading
单调加载试验结果中D0,0.85和Dρv,0.85数据标准差较大,原因是C3-4 和C2-6 试件破坏时承载力已退化至幅值承载力的33%,换算为承载力幅值85%时破坏指数显著降低。计算表明延性准则也能定义单调加载下柱的破坏,实现了单调加载与反复加载破坏准则的统一。
5 混凝土柱性能标准
低周反复加载柱的破坏可划分为4 个阶段:轻微破坏对应混凝土裂缝发育阶段(包括横向裂缝、垂直裂缝、斜裂缝的生成与发展);中等破坏对应保护层混凝土起皮剥落至大面积剥落;严重破坏对应核心区混凝土研磨、承载力大幅下降;失效/倒塌对应构件不能继续抵御地震作用并退出工作。
将包含详细试验现象描述的9 组29 根框架柱破坏曲线绘于图12 中,考虑试验中位移幅值的增量基本相同,曲线斜率即为柱的破坏速率,加载幅值越大破坏指数越大,破坏速度也越快。

图12 混凝土柱破坏曲线Fig. 12 Damage curves of columns
29 根框架柱的轻微-中等破坏临界点、中等-严重破坏临界点破坏指数见表6,平均值分别为0.21 和0.64。参考延性准则计算结果,建议失效或倒塌破坏标临界值为1.0。

表6 混凝土柱破坏特征点Table 6 Damage feature point of RC columns
根据承载力退化值、延性准则计算结果,参考国内外学者给出的混凝土柱破坏标准和延性准则破坏指数统计结果,给出了钢筋混凝土柱的延性准则评价标准,列于表7。
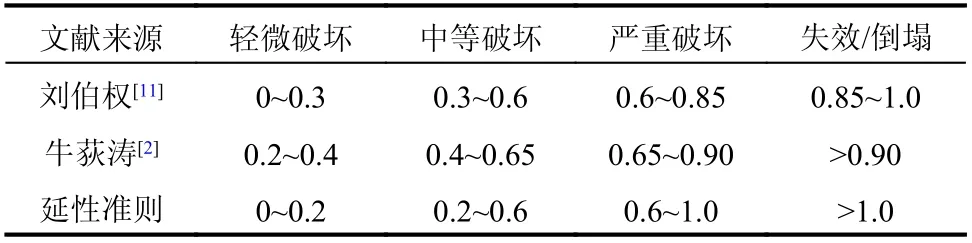
表7 延性准则破坏评价标准Table 7 Damage evaluating standards of ductility criterion
6 结论
本文对混凝土框架柱的变形能力与性能退化关系进行了研究,提出一种改进的混凝土柱延性破坏准则,结论如下:
(1)延性破坏准则考虑了变形能力强弱、轴压比、配箍率对性能退化的影响规律,将反复加载与单调加载两种加载方式组合到一个表达式中,能够较好地定义混凝土柱破坏。
(2)完成了105 组混凝土柱反复加载数据计算,Dρv,0.85组对应破坏指数平均值为0.963,标准差为0.354;完成了9 组单调加载试验数据计算,Dρv,0.85组破坏指数平均值为0.895,标准差为0.359。考虑配箍率影响和承载力退化幅值的Dρv,0.85组能够更好地定义混凝土柱的破坏
(3)将混凝土柱性能退化划分为4 个阶段,给出了对应的破坏指数分布范围,延性准则破坏评价标准与试验破坏现象吻合较好,可用于柱的破坏评估和预测。
