正交钢丝环链网片顶压力学行为薄膜等效方法
2021-11-17金云涛余志祥骆丽茹郭立平张丽君廖林绪
金云涛,余志祥,骆丽茹,郭立平,张丽君,廖林绪
(1. 西南交通大学土木工程学院,成都 610031;2. 陆地交通地质灾害防治技术国家工程实验室,成都 611756;3. 西南交通大学防护结构研究中心,成都 610031)
柔性防护系统广泛应用于地灾防护工程[1-2],常用正交钢丝环链网片(以下简称环形网)作为拦截部件。网片中网环单元间为接触式套接边界,接触区域外具有只受拉特性,冲击作用后将发生大变形[3],其计算方法是当前柔性防护领域的研究热点。
目前环形网数值模拟常用离散单元法[4-7]和有限单元法[8-10]。早期的数值模型往往将网片内部边界视作连续处理,如Nicot 等[11]提出了共节点的直杆单元模拟方法,实际上这也是网片模拟的主流近似方法,优点是计算效率高。Yu 等[12]和Hu 等[13]建立了环形网的离散接触态环梁单元数值模型,提出了等效面积条件下软化弹性模量的本构关系,该模型大大提高了网片力学行为的模拟精度。罗祥等[14]比较了网片数值模拟中等效面积法和力的平均分配法,并通过理论分析得到圆环等效截面半径的计算方法。郭立平等[15]揭示了网片面外加载过程中的力流传递特征,据此提出了一种基于力流等效的环形网解析计算方法,便于工程简化设计使用。上述研究推动了柔性网计算理论的发展,但发展更高效率并兼顾精度的环形网数值计算方法依然是当前的关注重点。
虽然环形网的网环单元间具有离散滑移特征,使得单元间的相互运动变得非常复杂,但由于单元几乎处于仅受拉状态,这也使得单元受力得以简化。这使得网片受到面外荷载作用时与薄膜具有很强的相似性,Mentani 等[16]的研究初步利用了这种相似性,使得非线性计算大大简化,同时获得了与试验较为相似的宏观力学响应,但Mentani 等[16]没有给出相似等效的解析论证,且其等效网型是菱形网。
为此,开展了3 m×3 m 环形网片的面外加载试验,研究了试件的P-Δ特性,据此分析并揭示了网片的正交拉力带传力特征。基于网片等效力学模型和薄膜最短传力路径假定,建立了薄膜面外加载过程的解析模型,研究了等效薄膜的本构关系,推导得到各规格网片的等效应力-应变曲线,并建立了基于等效方法的数值模型,实现了网片在静载与冲击荷载作用下的高效计算。
1 网片力学行为
1.1 试验概述
环形网片面外顶破试验在西南交通大学防护结构研究中心开展,试件尺寸为3 m×3 m,包括R5/3/300、R7/3/300、R9/3/300、R12/3/300、R16/3/300和R19/3/300 6 种规格,每种规格3 个试件。
试验设备主要为由钢结构反力架、液压千斤顶、位移传感器、加载单元和顶破头组成的150 t拉力顶破机(图1),顶破头为加载装置与网片直接接触的部分,用于传递荷载。
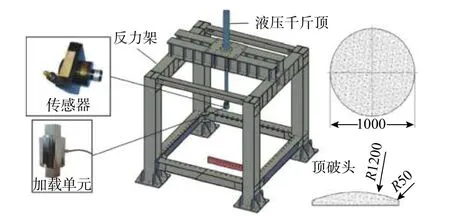
图1 试验设备Fig. 1 Test equipment
1.2 试验结果
网片试件通过卸扣与试验台相连,顶破头在试件布置好之后被推入网片中心区域下方,并与液压杆连接。加载时,顶破头提升速度为6 mm/s,通过位移传感器同步采集提升位移,由后台数据采集仪记录生成F-D曲线,直到网片破坏。如图2所示为不同加载阶段环形网片的形态。
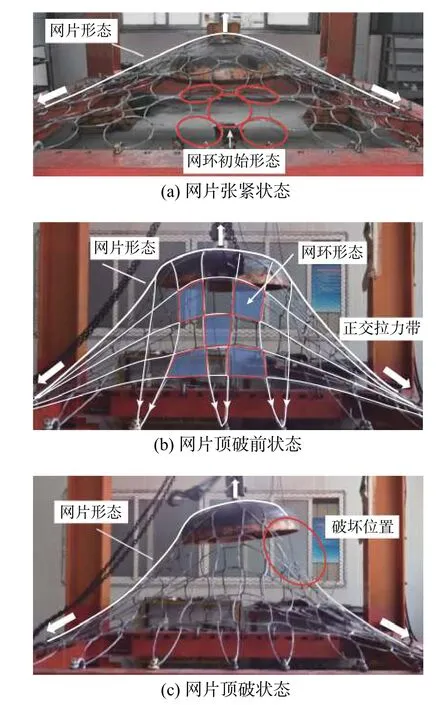
图2 试验中的网片形态Fig. 2 Mesh form during test
通过传感器采集得到的力-位移曲线如图3(仅列出R5 规格,其余规格曲线特征相似)所示,具体顶破力和顶破位移见表1。
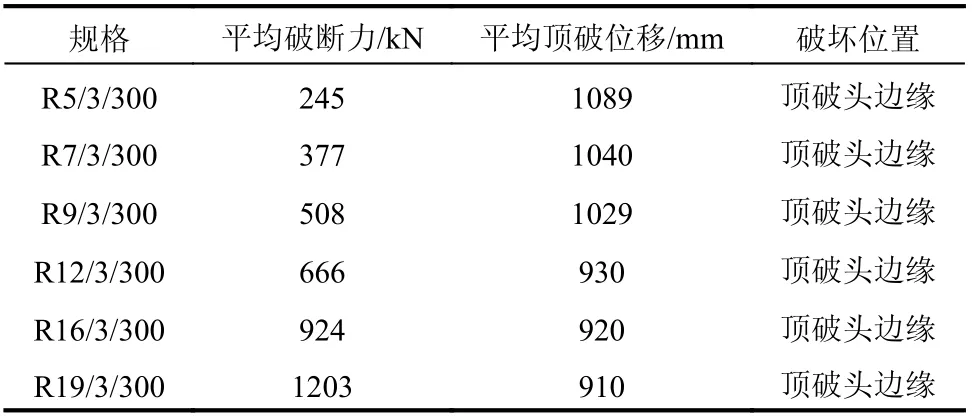
表1 顶破力和顶破位移结果Table 1 Test result of ultimate force and displacement
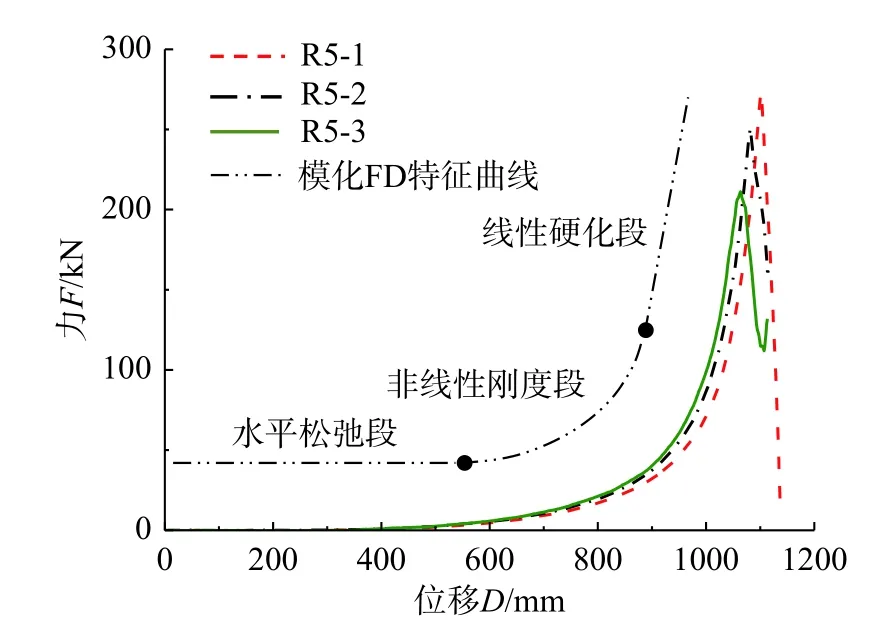
图3 R5 网片面外加载力-位移曲线Fig. 3 Out of plane loading F-D curves of R5 ring net
分析易知,力位移曲线具有三段特征(图3):阶段Ⅰ近似为水平直线,因初始松弛影响,网片刚度几乎为0;阶段Ⅱ为曲线,因受网环间嵌套约束影响,网片刚度显著增加,表现出明显的非线性受力特征;阶段Ⅲ为斜直线,因网环钢丝束进入轴向拉伸主导阶段,网片表现出较大的整体刚度,线性化受力特征较为明显。最终,因为加载顶头边缘对网环的“咬切”破坏,网片到达极限承载力。
1.3 网片-薄膜相似性
环形网受力后呈正交索网状态,内部网环均具有4 个传力点(图4)。网环在受力初都呈环状(图2(a)),接近极限状态时呈矩形(图2(b))。这是由于随着荷载增大,网环间滑移会趋于稳定,此后网环单元产生弯直变形,网孔逐渐变为矩形,由于单元拉力沿着轴线方向,因此形成了正交化内力分布模式(图4),相邻平行方向的网环钢丝束形成了正交拉力带,其传力方式类似正交索网。

图4 网片与薄膜的拉力带分布Fig. 4 Orthogonal tension band formation
根据试验结果分析易知,环形网的F-D曲线表现出由强非线性渐变为线性刚化的特征,这在宏观上与薄膜具有相似性[17],同时,环形网拉力分布与薄膜在相同边界条件下的拉力分布亦具有相似性(图4),且近似呈正交分布。因此,若能控制薄膜面外加载时具有与网片宏观上一致的F-D关系,即控制薄膜与环形网具有相同的张拉刚度(见式(1))便可实现两者的等效,这将大大简化离散网环间的接触非线性关系,提高计算效率。

式中:Kmem为等效薄膜面外加载刚度;Ki-rope为网片中各钢丝束沿加载方向的刚度;m为钢丝束数量。
2 薄膜等效模型
2.1 解析模型
薄膜等效的关键是确定本构关系,为此,基于薄膜正交拉力带分区假定(图5(a)),建立解析模型。膜刚度主要来自张拉应力,形成张力刚度,I 区应力普遍较低,甚至存在松弛,因此根据应力分布特征,忽略I 区刚度贡献。假定加载中任一时刻拉力带由两条直线段和一段圆弧组成(图5(b)),顶头位移为D,顶头与薄膜竖向接触力为F,Ⅱ区长度为l,宽度为b(初始宽度取顶破头顶压宽度d=1 m),铅垂面内的投影高度为h,厚度为t,与水平面夹角θ。实际顶头矢高h0=0.109 m,弧长Lr=1.032 m。设局部坐标系y轴沿Ⅱ区拉力方向,x轴为Ⅱ区拉力带宽度方向,z轴沿薄膜厚度方向(图5(b))。解析模型满足几何条件:

图5 拉力带解析模型Fig. 5 Tension band analytical model

设材料原长和终长为L0和L1,各中间历程的长度分别为L01、L02、···、Ln-1、Ln,对应变增量积分,可得真实应变:

式中:Fy为Ⅱ区拉力带拉力(图5);σy、εex、εez分别为拉力带y向应力,x向和z向名义应变。式(11)中εex、εez的确定与采用的本构关系类型有关,由式(9)和式(11),若已知F、D和本构关系类型,可求得相应σy、εty,即可求得薄膜应力-应变曲线,即:

此外,为确定薄膜等效厚度,遵循分布质量一致原则,密度ρ 取环形网钢丝密度7850 kg/m3。则薄膜厚度t0根据质量一致原则确定:

式中,mn为n圈规格环形网每1 m2质量。每种规格网片相应的等效薄膜厚度如表2。

表2 不同规格网片对应的薄膜厚度Table 2 Membrane thickness of different mesh sizes
2.2 薄膜本构关系
由于网环单元间初始具有松弛滑移特征,且这种松弛滑移产生的变形具有不可恢复性,因此构建本构关系时,采用了拟塑性假定,即假定屈服应变为0,加载后材料直接进入屈服平台,随后进入强化段。由于塑性变形不引起体积改变[19],因此引入塑性变形的体积不变条件:

式中:σ、ε 为薄膜的应力及应变;M、N为只与网环圈数n相关的量;e 为自然常数。
计算时,取弹性模量E为各应力-应变曲线失效点处即图6 中各曲线应变最大的数据点处的切线模量,由于计算得到的各圈数“n”对应薄膜的弹性模量取值差异不大,统一取其平均值11 000 MPa,泊松比取0.3。各圈数“n”对应的薄膜失效应变取图6 中各失效点横坐标,并采用线性拟合得到失效应变关于“n”的计算公式:

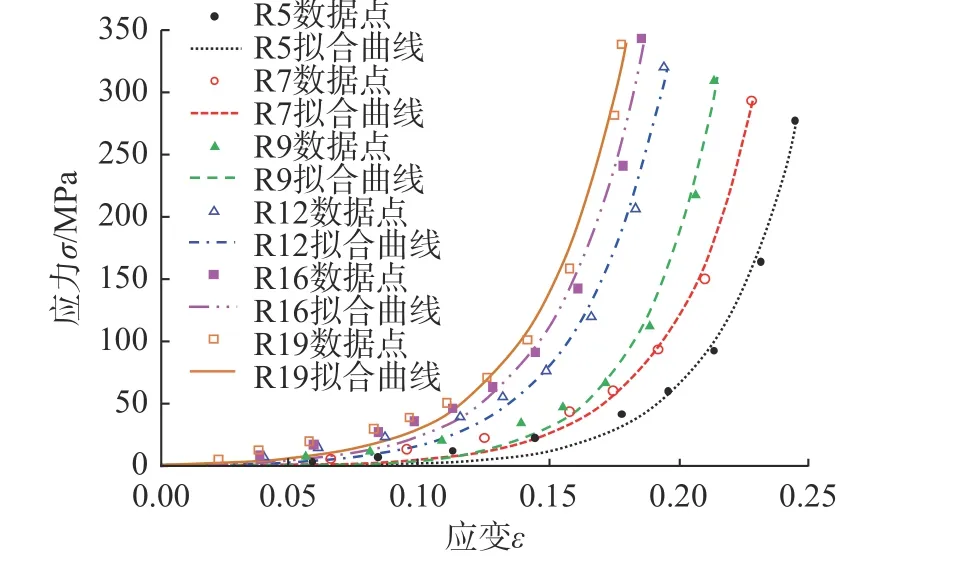
图6 拟合的薄膜指数强化本构模型Fig. 6 Exponential hardening constitutive model of membrane
2.3 数值模型
薄膜等效的目的是提高网片的非线性计算效率,其求解过程依托数值计算方法,因此需构建相应数值模型。采用显式瞬态动力非线性分析软件LS-DYNA 进行计算,采用Belytschko-Lin-Tsay单点积分四边形壳单元[20-21],由于单元厚度约为0.42 mm~1.58 mm,与平面尺寸相差3~4 个数量级,其弯曲及剪切刚度的贡献可忽略不计。薄膜周边铰接约束,顶破头指定向上的强迫位移,薄膜和顶破头的接触为采用罚函数和库伦摩擦模型的面-面接触,摩擦系数0.4(图7)。薄膜材料采用2.2 节所述指数强化本构,将薄膜应力-应变曲线(式(18))输入至数值模型,失效应变取值参考式(21),薄膜等效厚度取值见表2,网格尺寸25 mm×25 mm。

图7 薄膜面外加载有限元模型Fig. 7 FEM model of membrane out of plane loading
同时采用文献[13]中的等效面积法建立环梁模型进行对比分析。以R5/3/300 规格的网片为例,将薄膜等效、环梁模型和顶压试验结果进行了对比(图8),曲线与横轴包围的面积即网片的极限耗能。其余规格网片的结果对比见表3。综合比较来看,环梁模型得到的加载曲线与试验曲线贴合程度更高,但带来更高的计算消耗,等效方法的加载曲线同样能够还原出初始松弛段、非线性刚度段和线性硬化段的3 阶段特征。等效方法的顶破力、顶破位移、极限耗能等指标相对误差均小于10%,精度与环梁模型相当。值得注意的是,等效方法得到的顶破位移均略小于试验值,这是因为薄膜等效解析模型忽略了Ⅰ区刚度贡献,然而数值计算时,Ⅰ区刚度客观存在,因此导致顶破位移小于试验值。但两者差异很小,最大误差仅为6.6%,这也说明解析模型等效时忽略Ⅰ区刚度贡献是合理的简化。

表3 网片面外顶破的等效方法误差对比Table 3 Relative error contrast between equivalent method and circular beam model

图8 等效方法力-位移模拟结果对比(R5/3/300)Fig. 8 Simulation results of equivalent method (R5/3/300)
3 等效方法验证
3.1 网片冲击试验验证
为了进一步研究等效方法用于冲击荷载作用下的适应性,结合Grassl 等[22]的试验研究进行了反演分析。Grassl 进行了网片在固定边界下的冲击试验,网片平面尺寸3.9 m×3.9 m,网环规格R7/3/300,四边固定于刚度很大的支撑钢框架,冲击试块为球体,直径0.88 m,质量830 kg,冲击能量45 kJ,试验通过高速摄像机和固定于试块上的加速度传感器得到试块冲击过程的位移、速度、加速度时程曲线。
分别建立环形网片冲击试验的离散接触态环梁有限元模型和薄膜等效数值模型。环梁模型的模拟方法为文献[13]中的等效面积法,采用其所述软化弹性模量的应力-应变曲线,网环间为通用自接触,单个网环分为16 段梁单元。薄膜等效模型中薄膜材料参数采用2.2 节所述的指数强化本构模型,应力-应变曲线参考式(18),失效应变取值参考式(21),薄膜划分的网格尺寸25 mm×25 mm,模型的具体输入参数见表4。薄膜等效模型和环梁模型在各冲击时刻下的形态如图9 所示。

图9 薄膜和网片形态及应力云图Fig. 9 Form and stress nephogram of membrane and ring net

表4 等效模型输入参数Table 4 Input parameters in equivalent numerical model
数值模型的计算结果中,t=0.06 s 时,薄膜与网片形态存在微小差异,这是由于环形网的初始松弛影响导致其垂度略大于薄膜初始垂度。t=0.1 s时,网片开始张紧,刚度发展迅速,网片和薄膜变形形态趋于一致。t=0.15 s 时,落锤到达最低点,薄膜和网片的拉力带效应显著,具有明显正交化受力特征,该阶段试件刚度发展至极大值。
模拟结果与文献[22]的试验结果进行了对比,冲击试块位移、速度、加速度时程曲线结果对比如图10。对比表明,薄膜等效方法得到的加速度峰值与试验结果相对误差仅为4.3%,离散网环模型得到加速度峰值与试验结果相对误差为3%,两种数值模拟方法的精度相当。值得注意的是,由位移及速度时程曲线可见采用离散网环模型时,明显高估了试块的回弹高度,表明冲击过程网片的耗能和弹性储能占比不合理,因此在这点上薄膜等效模拟方法反而具有一定优势。
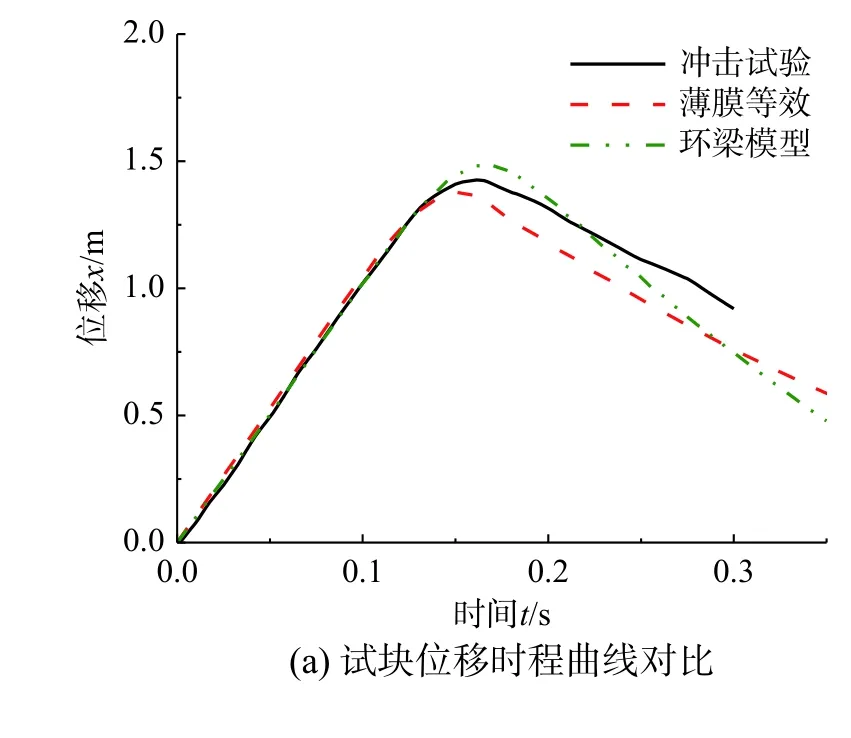

图10 试块运动参数对比Fig. 10 Contrast of block motion parameters
3.2 计算效率
对比3.1 节中离散接触态环梁模型和薄膜等效模型的计算耗时(表5)表明,薄膜等效可以大幅提高环形网的计算效率,测试模型中等效方法计算速度提高10.3 倍。实际上,随着环形网片计算规模的增加,由于环梁模型内部自接触导致的计算资源消耗将显著增加,薄膜等效的优势将更加显著。
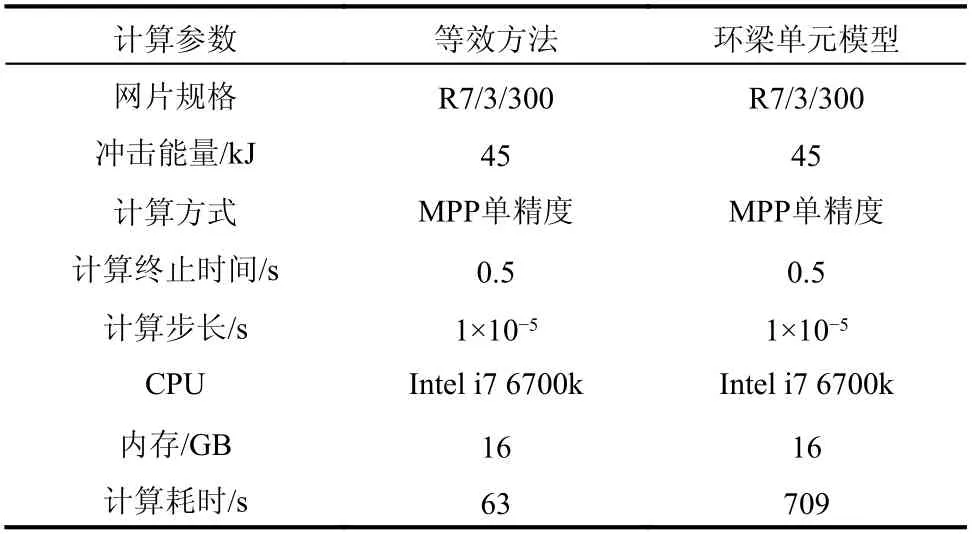
表5 计算效率对比Table 5 Contrast of computational efficiency
4 结论
综上所述,可以得到以下结论:
(1)环形网片加载过程中拉力带效应具有显著的正交化受力特征,其F-D关系的三阶段特征可以通过指数强化本构反演,并结合壳单元薄膜比拟实现力学行为等效。
(2)薄膜等效计算与拟静力试验结果的顶破力、顶破位移、耗能误差均小于10%,等效方法能够比较准确地反映环形网片面外加载的宏观力学行为。
(3)薄膜等效方法得到的试块冲击变形、速度和加速度时程与试验结果基本一致,其中加速度峰值误差为4.3%,精度与离散接触态环梁模型相当,且等效方法计算效率可提升10 倍以上。
复杂边界条件下特别是柔性可滑移边界下的薄膜等效模拟方法需要进一步深入研究。
