永磁直驱风电机组网侧PWM变流器的建模与仿真
2021-11-17国网浙江省电力有限公司台州供电公司曾诚实张慧杰
国网浙江省电力有限公司台州供电公司 曾诚实 张慧杰
电力电子变流器是风电机组系统的关键设备之一。随着电力电子器件技术的发展,电力电子变流器在改善风电机组系统性能方面具备了巨大的发挥空间。背靠背PWM变流器作为目前主流的三相变流器,由于它在某种程度上能实现了电网与风电系统之间的解耦,并能独立调节有功和无功功率,在风电系统中的应用也愈发广泛。
本文主要研究了永磁直驱风电机组背靠背PWM变流器的基本结构,推导了变流器的数学模型,并设计网侧变流器的控制方案。通过调节背靠背变流器的直流侧电压,实现了风电机组发出的有功功率向电网的及时有效传输;通过控制网侧变流器的无功电流分量,实现对无功功率的解耦独立调节。通过在MATLAB/Simulink中建立仿真模型,根据仿真结果验证了该系统模型的正确性和控制策略的有效性。
1 背靠背变流器的拓扑结构
背靠背变流器与发电机侧相连的变流器通常被称作机侧变流器;而与电网侧相连的一般称作网侧变流器。一个带电容装置的直流母线将两个变流器连在一起。中间的电容具有电磁隔离作用,保证两侧的变流器能够分别控制而不会出现干扰耦合状况。
从控制系统的要求来说,变流器应具有双向传送及四个象限的控制能力。双向的意思是功率能够往任何一边传送,它的能量既可以从发电机侧往电网侧传送,又可以从电网侧向发电机侧反向传送。而四象限指变流器能够运行在正负电阻及纯电容和纯电感这四个象限。

图1 网侧PWM变流器结构图
2 网侧PWM变流器的数学模型

式(3)即为网侧PWM变流器的在abc坐标中的数学模型,可见在电网电压给定后,通过控制开关函数就可以调节直流环节的输出和交流电流的输入。但是式(3)中的变量都是随时间变化的交流量,不利于控制系统的设计,所以需要将上述方程进行坐标变换。
将式(3)经过3s / 2s坐标变换,再经过2s / 2r坐标变换,就可得到变流器在dq坐标系中的数学模型如下:

在经过dq坐标系变换后,由于电感作用,使得dq两个轴的电流之间存在耦合,相互会产生影响。因此,在对网侧的控制器设计的过程中,需要通过解耦实现单独控制id、iq。
3 网侧变流器控制策略
网侧变流器的主要控制目标是保持中间母线的直流电压稳定。在dq坐标系下的电流矢量控制策略,是经过矢量坐标定向后,利用电流id和iq分 别调节母线电压idc和无功输出,同时通过前馈控制环节使id环的调节速率加快。
控制系统如图2所示。

图2 网侧变流器控制系统
通过推导,可以得到变流器的有功和无功功率为:

式中,id、iq分 别为网侧变流器的有功电流分量和无功电流分量,分别独立调节id、iq就可以实现系统有功功率和无功功率的独立解耦控制,并且P、Q的正负体现了变流器不同的功率传输特点。
4 仿真模型及结果分析
在风力发电的变流器控制系统中,变流器的调制方式具有关键的作用,它的调制深度与直流电容电压的利用率直接相关。目前主流的PWM控制技术主要有正弦波调制(SPWM)和空间电压矢量调制(SVPWM),它们主要目标是使输入电流成为正弦量,并且让系统运行于单位功率因数。SPWM是通过正弦基波与三角载波的比较,用它们的相交点来控制开关的开断,其出发点就是为了得到更好的正弦波。而SVPWM是根据空间矢量的切换来得到圆形磁场,相对于SPWM方法,不仅能获得高质量的正弦波,还具有提高直流电压利用率、提高交流电机性能、减少转矩脉动等优势。
根据上文所推导的网侧变流器数学模型,结合SVPWM控制算法,将设计的变流器矢量控制策略模型化,并对其进行仿真验证。
根据主电路参数的选取原则综合考虑,设置的仿真参数如下:
交流侧的相电压幅值为380V,频率为60Hz,电网侧的电阻为0.2Ω,电感为2mH,直流电容为1.8uF,中间直流参考电压为700V。另外将逆变侧变流器看成是一个电阻和一个反电动势叠加。通过调节反电动势的大小,可以控制网侧变流器运行于整流状态或逆变状态。
图3 为网侧变流器的整体仿真模型。

图3 网侧变流器仿真模型
仿真开始时设定为正向功率运行状态,在0.2s时通过对电压源施加一个阶跃响应,使电压从500V阶跃至800V,从而改变功率流向。
根据仿真结果,在0.2s突加一个阶跃响应后,变流器的电压经过一个短暂的调整后会较快回到设定值附近,表明该变流器系统具备良好的鲁棒性。在直流电压的控制中,d轴电流是主要的参与者,这可以从图4得到。而图5中,在0.2s之前变流器的电压和电流同相运行,而0.2s状态改变后,变流器的电压与电流相位开始相反。从图6中有功功率的变化曲线也可以看出,当0.2s后功率流向改变,从吸收功率变为发出功率,对应于图5及图6的变化。

图4 id及iq曲线
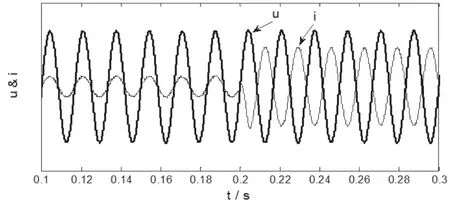
图5 A相电压电流

图6 变流器输出功率
结论:本文针对永磁直驱风电机组的背靠背PWM变流器基本结构进行了探讨。通过推导变流器的数学模型,并对网侧PWM变流器的控制策略进行了研究,利用坐标变换实现了对系统有功功率和无功功率的独立解耦控制。最后在MATLAB/Simulink中建立仿真模型,验证了仿真模型的正确性和控制策略的有效性。
