轨道摄影机器人瞬时转弯半径分析

谢志坤，韩 军，冯虎田

(南京理工大学机械工程学院，江苏 南京 210094)

随着社会经济的发展，人们的业余生活越来越丰富，对精神生活的追求也更加迫切。为了丰富电视节目的拍摄方式，增强画面的冲击力，使观众充分享受视觉的盛宴，影视制作单位对摄像设备提出了更高的要求[1-3]。伴随着软件技术和硬件的成熟和发展，虚拟演播室为实现节目制作的全新视觉效果提供了技术手段，越来越受到影视创作者及其相关人员的青睐，而在虚拟演播室系统中，镜头的跟踪和拍摄扮演着至关重要的角色。

为了将虚拟演播技术与摄像画面实时结合，对摄影机的拍摄轨迹要求十分严格，纯粹通过人工操作是无法达到标准的，而轨道摄像机器人在拍摄中可以突破场地条件的制约和人工拍摄的自然限制，能够在运动的同时完成镜头变/聚焦，而且通过采用软硬刹车技术，可以保证在启动、运动、停止时不出现画面晃动的情况[4-7]。本文对轨道摄影机器人弯轨运动的瞬时转弯半径R进行分析，通过对轨道摄影机器人的底盘运动学分析和动力学建模，得到轨道摄影机器人瞬时转弯半径R和输入变量的关系式[8]。

1 轨道摄影机器人坐标系建模

图1所示的轨道摄影机器人运动的局部坐标系为XZ-Z-YZ，该局部坐标系固定于轨道摄影机器人的质心处，XZ轴沿轨道摄影机器人小车部件车身的纵向对称轴方向，XZ轴正向即小车的移动方向，YZ轴沿摄影机器人车身的横向对称轴方向，垂直于XZ轴。X-O-Y为全局坐标系，原点O固定于地面或者轨道起点处，是轨道摄影机器人运动的绝对坐标系。

图1 轨道摄影机器人全局坐标系和局部坐标系

在轨道摄影机器人的局部坐标系(图1)中，VZ为轨道摄影机器人的质心速度；θ为轨道摄影机器人小车航向角，即全局坐标系中小车质心速度与X轴的夹角；β为轨道摄影机器人小车的质心偏向角，即局部坐标系中小车质心速度与车头指向(XZ轴)的夹角；φ为车辆横摆角，其值为航向角与质心偏向角的差值，即θ=β+φ。

由基本运动学方程可知，轨道摄影机器人的弯轨运动瞬时转弯半径R为

(1)

式中：a为轨道摄影机器人质心的向心加速度。通过图2所示的位置检测装置，利用传感器可以测得机器人当前的位置及速度VZ。而轨道摄影机器人的向心加速度主要由轨道对轮子的作用力合力产生，此合力是一个未知量，需要进一步分析求解。

图2 位置检测装置

2 轨道摄影机器人的动力学分析

2.1 轨道摄影机器人的整体动力学方程

轨道摄影机器人的动力学建模如图3轨道摄影机器人局部坐标系所示。图中：FX为轮子所受合力在轨道摄影移动机器人局部坐标系XZ轴方向的分力；FY为轮子所受合力在轨道摄影移动机器人局部坐标系YZ轴方向的分力；L为轨道摄影机器人轮系轴距；LF为质心到前轴的距离；LR为质心到后轴的距离；D为轨道摄影移动机器人的轮距；ax为移动机器人XZ轴方向的加速度；ay为移动机器人YZ轴方向的加速度。

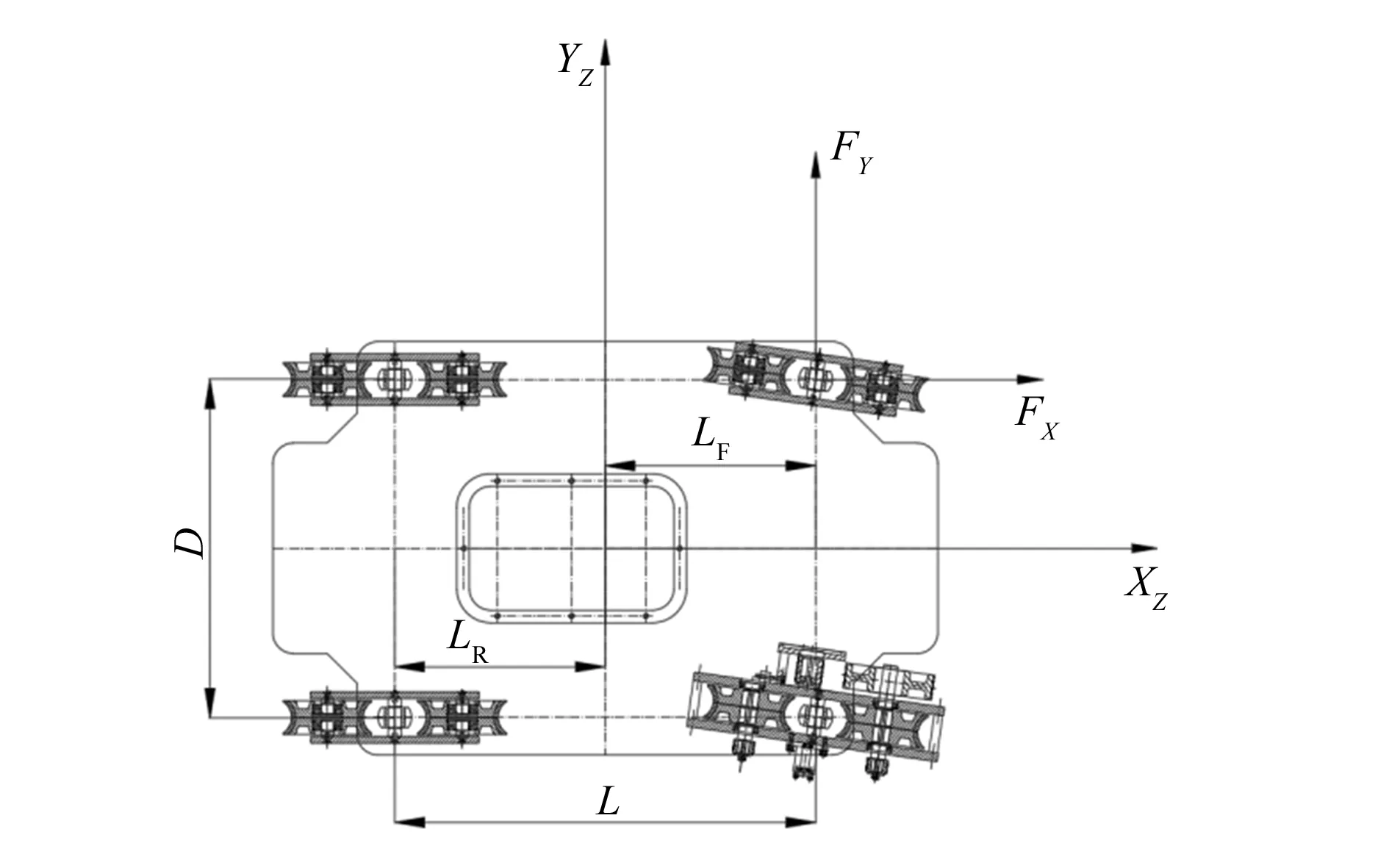
图3 轨道摄影机器人局部坐标系

根据达朗贝尔原理，由图3可知，轨道摄影机器人在四轮移动机器人坐标系的XZ轴、YZ轴、Z轴的平衡方程如下：

(2)

(3)

(4)

式中：m为轨道摄影机器人的总质量，kg；IZ为轨道摄影机器人绕质心轴的转动惯量，kg/m2；ωR为轨道摄影机器人的横摆角速度。从式(1)、(2)可知，为求解轨道摄影机器人弯轨运动的曲率半径，需得到机器人整体YZ轴上的加速度，因此要进行单个车轮转角受力分析。

2.2 轨道摄影机器人的车轮转角分析

由于路面的侧向倾斜，在运动阶段轮系移动机器人受路面的倾斜角度、侧向阻力或者转弯时的离心力等因素的影响，车轮中心沿车轴方向产生一个侧向力F。由于车轮与地面接触部分为弹性体材料，所以当F小于车轮与地面间的最大静摩擦力f时，车轮发生弹性形变，产生倾斜角度，如图4所示，导致车轮行驶方向偏离预定的行驶路线，这种现象称为轮胎的侧偏现象。而在轨道摄影机器人中，移动轨道摄影机器人的移动底盘车轮采用的是双圆弧的轮轨型面，车轮的结构如图5所示，车轮外圈材料为聚氨酯。聚氨酯是一种介于塑料和橡胶之间的弹性体，机器人在弯轨运动阶段，由于轨道的挤压以及车轮本身材料的性质，车轮转向会受到轨道侧向力作用，聚氨酯外圈产生变形，使车轮出现略微倾斜，导致车轮的行驶方向与轨道切线方向产生偏移，类似于轮胎的侧偏现象。车轮的变形同样会与车轮平面错开一定距离，且产生倾斜角，所以普通轮胎的侧偏现象对轨道摄影机器人的轮子同样适用。

图4 轮胎侧偏现象 图5 轨道摄影机器人车轮结构

由图6几何关系可知，Vi为四轮全向移动机器人车轮的实际速度；Fs为车轮运动时与轨道的摩擦力，沿着车轮转动的平面方向；Ft为车轮运动时轨道对车轮的反向作用力，垂直车轮转动平面；α为车轮偏转角度；δ为轮胎偏移角；ε为参考变量。其中车轮转角α由轮子上安装的传感器测量得到。

Fa=Ftcosδ-Fssinδ

(5)

下面对Fs，Ft，δ这3个变量进行分析求解。

轨道摄影机器人在弯轨上运动时，会出现爬升现象，如图7所示，对轮轨竖直截面进行受力分析，FN为轨道对车轮的反向作用力，将其进行分解可得到沿车轮径向的支持力Fn(该力可由轨道摄影机器人的质量求得)以及垂直于车轮的作用力Ft，FN与竖直方向的夹角为η，根据受力分析可知:

Ft=FNsinη=Fntanη

(6)

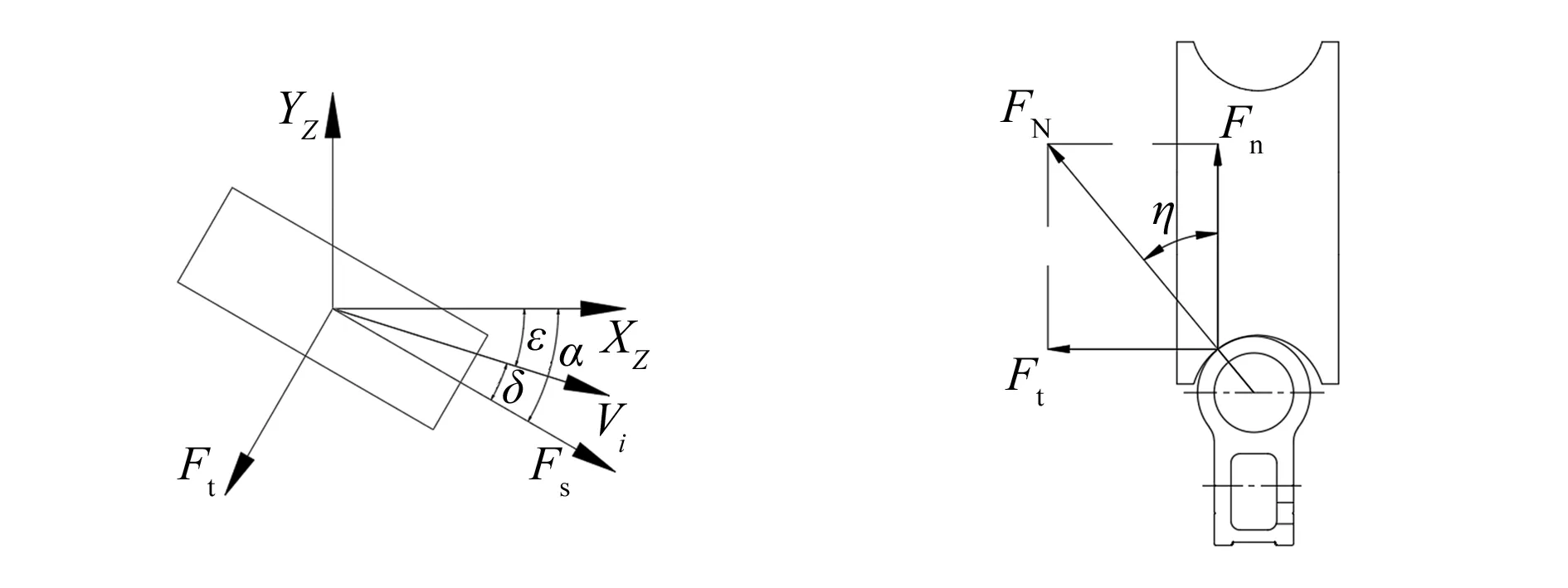
图6 轨道摄影机器人单轮地面投影坐标系 图7 轮轨简化模型

为得到η值，建立车轮在轨道上爬升的简化模型，将轮对上移一定距离，与轨道分离。给轮对一定的横移量W，即将左右车轮踏面移动一定距离，如图8所示，在已知车轮和轨道结构尺寸的前提下，可以建立实际滚动圆半径RW和横移量W的关系。对于车轮的滚动圆半径RW，利用各轮的速度V及电机转速n可求解得到，即

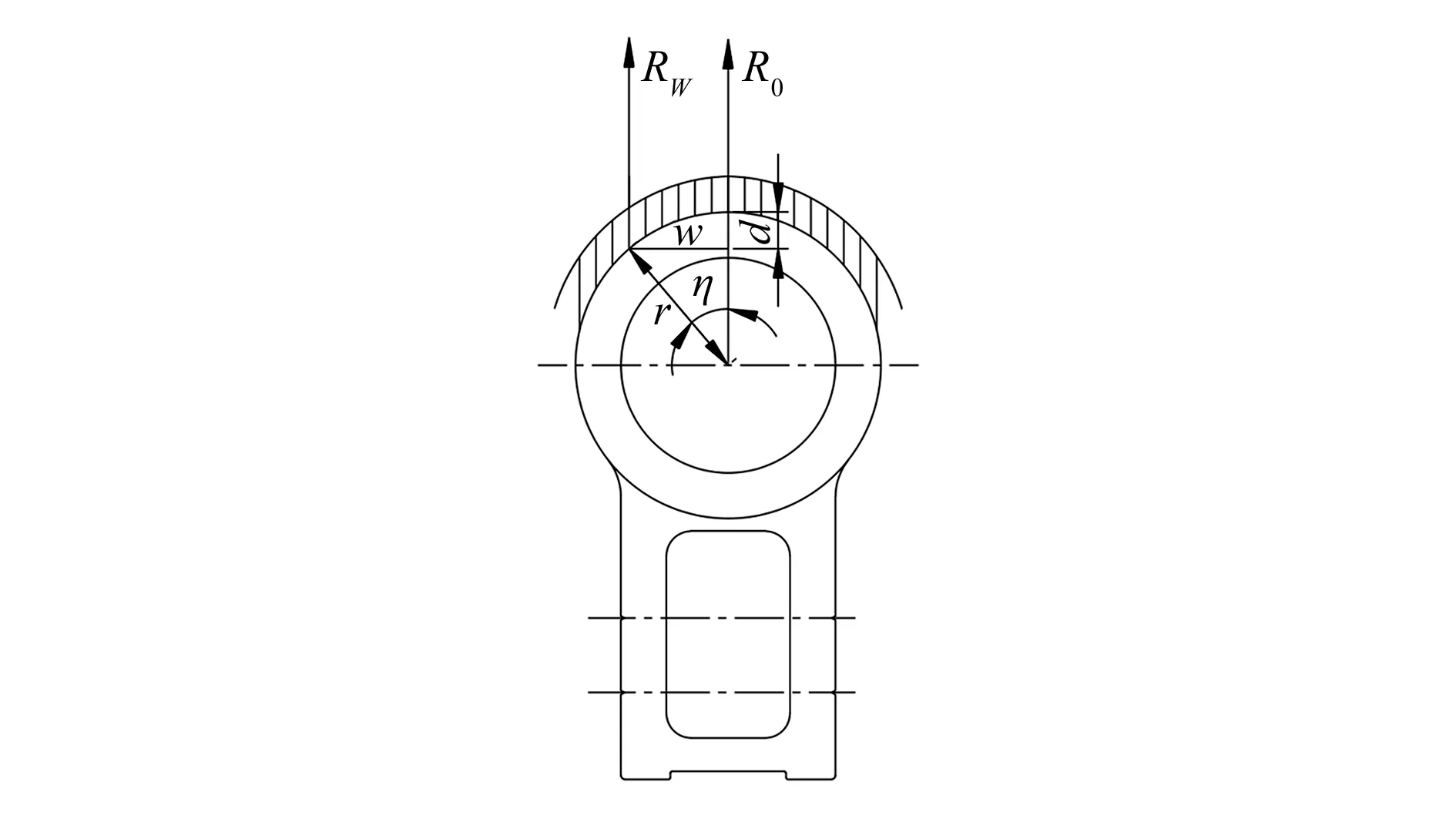
图8 车轮爬升简化模型

(7)

根据式(7)可得实际滚动圆半径RW和横移量W的关系如图9所示。其中：

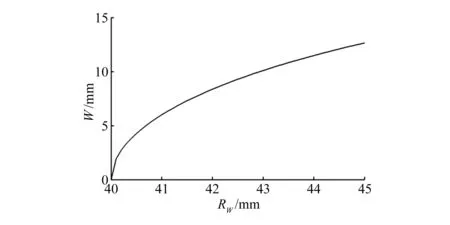
图9 车轮滚动圆半径与横移量的对应关系曲线

(8)

由图8可知，已知R0和RW，即可求出η值。

(9)

因此，式(9)联立式(6)可得

(10)

式中：Fti为4个轮子垂直于车轮的作用力，i=1,2,3,4。

由图6的几何关系可知，α，δ和ε间的计算公式为：

δ=α-ε

(11)

为了简化轨道摄影机器人运动模型，在轨道摄影机器人转向运动过程中，假设机器人质心前进速度与前轮和后轮前进速度相等，即：

Vicosεi=VZcosβ

可得

(12)

式中:εi是4个轮子的参考变量，i=1,2,3,4。

其中各个车轮的速度Vi通过速度检测装置测量得到，联立式(11)和式(12)可得

(13)

式中：δi为4个车轮的偏移角，i=1,2,3,4；αi为4个车轮的转角,i=1,2,3,4。

系统在平面上侧向运动的动力学方程为:

(14)

(15)

将β提取出来得：

(16)

将式(16)代入式(13)，可得

δi=αi-

(17)

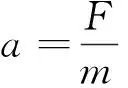
(18)

因此可得到机器人质心的向心加速度，将加速度式(18)代入式(1)得到质心的瞬时转弯半径R：

(19)

3 结果验证

为验证质心瞬时转弯半径R公式的正确性，建立轨道摄影机器人的三维模型，如图10所示，对其进行轨道运动仿真。

图10 轨道摄影机器人三维模型

理想状态下，即车轮与轨道接触过程中没有变形现象产生，车轮无侧偏现象，轨道摄影机器人在弯轨部分运动时底盘的几何中心轨迹为轨道的同心圆，且轨道半径RP为：

(20)

式中：Rtri为内侧轨道中心线半径；Rtro为外侧轨道中心线半径。

选取轨道摄影机器人不同的运行速度进行仿真验证，将轨道摄影机器人运动过程中的参数代入瞬时转弯半径R方程式(19)，仿真参数见表1。

表1 运动仿真参数

利用MATLAB将机器人弯轨运动的各个参考点位置代入式(19)计算其转弯半径，整理统计所得的轨道半径，以弯轨入口点为起始点建立位置坐标系，如图11所示，图中曲线为内外弯轨中心线，在该坐标系的基础上建立轨道摄影机器人弯轨运动的运动轨迹拟合曲线，如图12所示。

图11 弯轨运动位置坐标系

图12 理想运动轨迹和拟合轨迹

从仿真结果可以看出，一方面，轨道摄影机器人在弯轨部分运动时，理想轨迹与由瞬时转弯半径R得到的拟合轨迹有偏差，该偏差主要由车轮的爬升现象产生，各个测量参数由于传感器自身精度因素也会增加相应误差；另一方面当轨道摄影机器人的行走速度增大时，其运动轨迹半径也随之增大。

由于该轨道摄影机器人主要应用于演播室、电视台等场所，对于弯轨段运动要求慢速平稳，以保证镜头的稳定性和画面的连续性，弯轨运动速度设计要求在500 mm/s以内，如果弯轨运动速度超过这个范围容易导致镜头晃动、画面模糊等情况，同时可能产生脱轨现象，目前正在对相关结构进行优化以改善或克服该现象的发生，因此正常拍摄条件下，弯轨运动速度应保持在300 mm/s以内。

从仿真结果可知，拟合轨迹与理想轨迹最大偏差在40 mm以内，最大偏差发生在轨道摄影机器人从直轨进入弯轨的过渡阶段，该阶段由于机器人运动时前后轮的偏转角度差距较大，因此拟合轨迹与理想轨迹有较大偏差。随着输入参考点的增多，拟合半径逐渐接近理想弯轨运动半径，拟合轨迹和理想轨迹偏差逐渐减小。从图12可得，正常拍摄条件下，即弯轨运动速度在300 mm/s以内时，拟合轨迹与理想轨迹偏差在15 mm以内。轨道摄影机器人进行实际弯轨运动时，其运动中心与理想轨迹中心(即弯轨的曲率中心)存在位置误差，该误差有待进一步研究确定，且考虑到实际运动时轮子的爬升现象产生的偏移，因此仿真结果满足预期要求，即轨迹符合机器人运动预期情况，从而验证了该瞬时转弯半径R方程的正确性。

综上所述，当轨道摄影机器人质量m、轨道弧面半径r、车轮滚圆半径Rt确定的情况下，可以通过检测输入向量[VZViαiωR]得到轨道摄影机器人的转弯半径R的动态输出值。

4 结束语

本文以轨道摄影机器人为研究对象，对机器人底盘在弯轨上运动的实时转弯半径进行分析，通过对轨道摄影机器人进行动力学建模、运动学分析以及车轮偏移角的研究，从而可通过检测输入向量[VZViαiωR]得到轨道摄影机器人的瞬时转弯半径R的动态方程，为轨道摄影机器人的轨迹规划提供了理论基础并为检测弯轨曲率提供了依据。