基于体素法的静态模型设计
2021-11-17杨继全施建平唐文来
杨继全,李 娜,施建平,唐文来,张 钢
(南京师范大学电气与自动化工程学院,江苏 南京 210023)
体素用于三维成像、科学数据与医学影像等领域[1],以特征节点作为体素,建立材料与节点的对应关系,然后建立实体模型,同时建立几何结构和材料组成模型,适用于内部材料与表面材料不完全相同的对象建模。近年来更新的工艺,为模型的使用提供了可能:多材料的3D打印技术可用于制造可折叠传感器[2],异质材料的低温集成化制造可以建立模型间的数据接口[3],使用多个压电喷头就可以开发出光刻3D彩色打印机[4]。
1 特征节点的获取
为准确描述异质零件内的材料分布,需要确定零件的结构特征节点和材料特征节点;为精细描述异质零件内的材料分布,还需要对零件的各特征节点进行适当插值细化[5]。
图1所示的是由锌(Zn)、铝(Al)、铜(Cu)3种金属材料构成的梯度功能材料平面模型特征节点网格划分,以轮廓特征节点构成外框架P1P5P11P10。材料特征节点P2、P3、P4、P6、P7、P8、P9的单种材料体分量均为1,另外两种材料体分量为0,再以这些材料特征节点构成细化特征节点,对模型进行适当细化。为提高材料分布的定义精度,还需对图1 所示的网格进一步细化,细化的原则是各原有节点的材料分布向量(即材料变化曲率),曲率变化越大,细分点越密集。
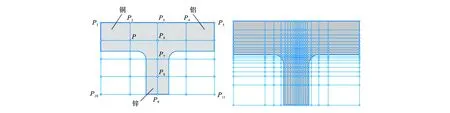
图1 异质零件平面模型特征节点网格划分和材料定义网格细化
2 材料特征节点定义
基于图1所示的网格划分和细化后的节点,建立STL模型的均匀点云数据集,构建空间微四面体,形成新型几何模型,依据该零件的物理特性和材料分布特征,对其进行材料设计。异质零件CAD模型中某点P,按照以下方法进行材料赋值。
(1)
式中:k为该模型所含材料的总种类数;αj表示节点P处的第j种材料的体分量,所有材料的体分量之和应为1,即
(2)
点Pi在x轴方向上第j种材料的体分量表示为
MPi=(αj,x)=αij
(3)
下面以二维平面内的多相材料分布设计为例,阐述多材料异质零件的材料设计过程。根据式(1)分别给图2 (a) 所示的由锌、铝和铜3种材料构成的多相材料片层进行定义及赋值,首先对该多相材料片层进行网格细化,获得一系列材料分布控制节点,然后分别对各控制节点进行材料赋值,其节点材料分布的赋值定义见表1。表中每个点的材料体分量总和均应满足式(2)。
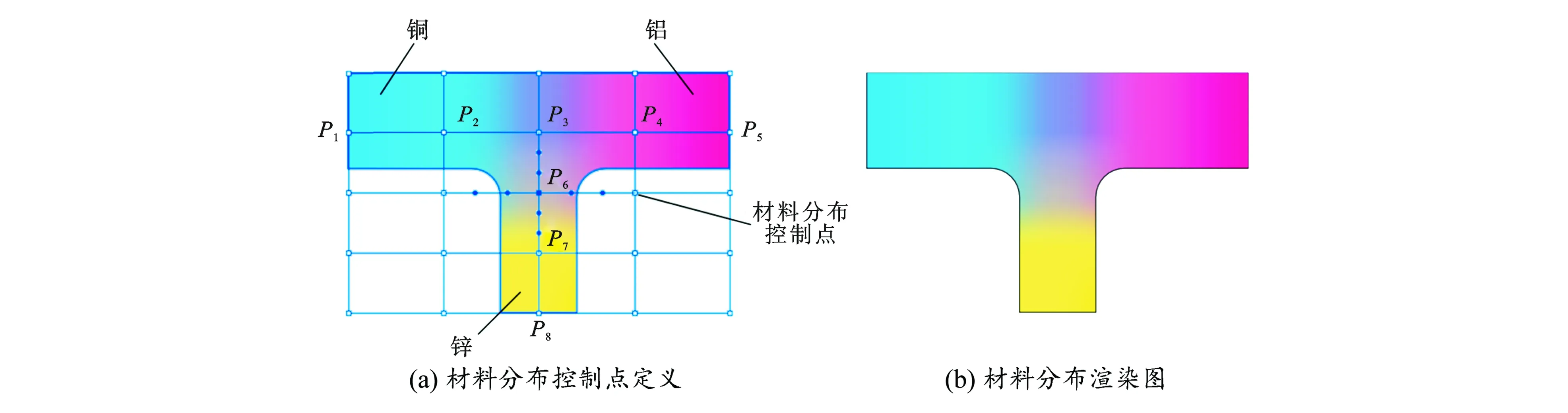
图2 材料分布定义

表1 节点材料分布赋值定义
则多相材料内任一点P的材料分布为
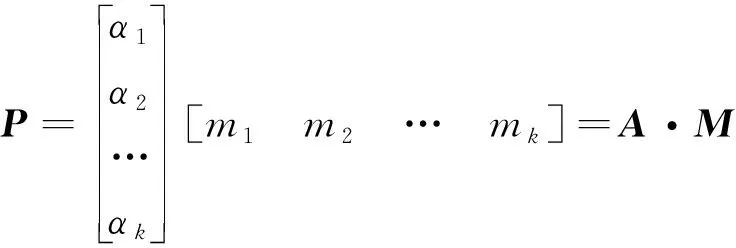
(4)
式中:A为材料系数矩阵;M为材料种类矩阵。
图2(b) 所示为赋值后形成的材料分布渲染图。
为提高材料分布的定义精度,还需对图2(a) 所示的网格进行进一步细化,细化后的模型如图3 所示。
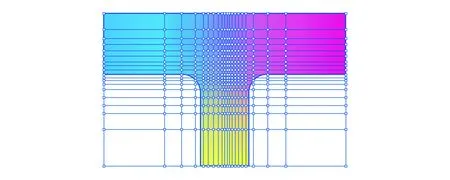
图3 材料定义网格细化
利用公式(1),按照表1所列的各特征节点的材料分布赋值定义分别对图4所示的各节点赋值,经插值计算得到图5所示的特征节点材料定义图,插值算法参见3节。
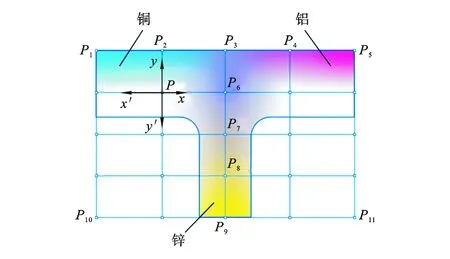
图4 特征节点材料分布定义
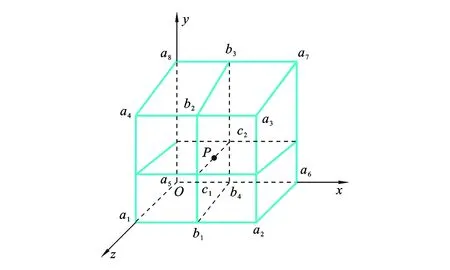
图5 空间节点P及相邻8 个节点插值计算得到的特征节点材料定义
3 节点间线性插值算法
基于特征节点的不同材料组分,对于非特征节点的材料属性,采用数值分析和计算机图形学领域的三线性插值方法来获得,即在三维散乱数据集的张量积网格上进行线性插值,这个张量积网格可能在每一维度上都有任意不重叠的网格点,但并不是三角化的有限元分析网格。其特性以及与线性插值和双线性插值的关系为:三线性插值在一次(n=1)三维(D=3)(双线性插值的维数D=2,线性插值的维数D=1)的参数空间中进行运算,这样就需要(1+n)D=8个与所需插值点相邻的数据点;三线性插值等同于三维张量的一阶B样条插值,其运算是3个线性插值运算的张量积。
如图5 所示,节点P坐标为(x,y,z),其邻近的节点分别为a1~a8,b1~b4,c1,c2,其最邻近的8 个相邻节点为a1~a8(由空间点云数据获得,由这些节点的信息通过插值算法才可以获得b1~b4,c1,c2,进而得到空间任意节点P的属性值),其中各坐标数值都是0~1之间的值,以S(k)表示节点k的属性值,则节点P三线性插值公式为
(5)
式中:S(ai)(i=1~8)、S(bi)(i=1~4)、S(ci)(i=1,2 )分别为ai,bi,ci的属性值。最后点P的属性值为
S(P)=S(c1)+z×[S(c2)-S(c1)]
(6)
根据上述节点赋值和节点间插值方法对细化网格进行材料分布运算,使用色彩表示材料进行可视化设计。根据实体的曲率等几何信息,实体的边界曲面首先被离散化为一系列单元网格(通常为三角形网格或四边形网格),可视化引擎再根据单元网格节点的三维位置及法向量逐一生成单元可视面片,进而实现整个边界曲面的渲染,如图6 所示。
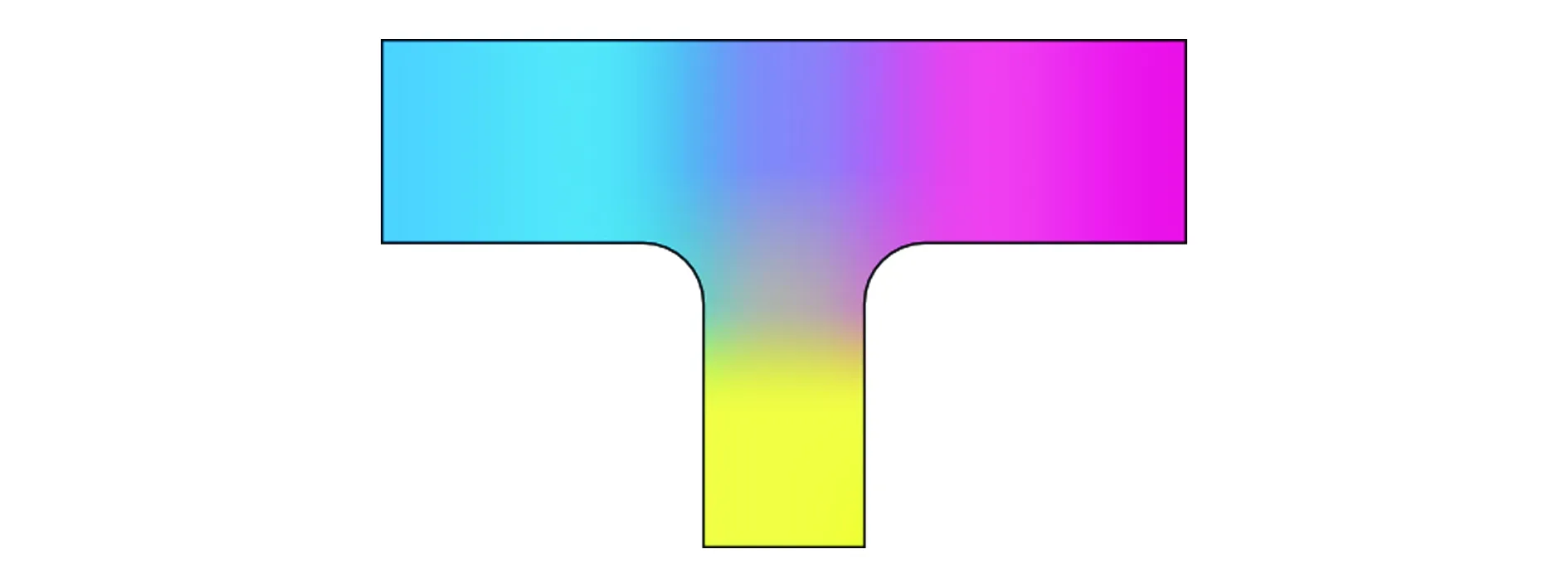
图6 节点材料分布渲染图
基于上述建模方法,设计一些异质零件,对该异质零件建模方法进行结构和材料分布的测试。图7 所示为异质零件的材料分布定义,图7(a)所示为三维模型,图7(b)所示为某切片层内特征节点,图7(c)所示为某切片层内特征节点的材料定义,图7(d)所示为基于特征节点的材料分布渲染图。
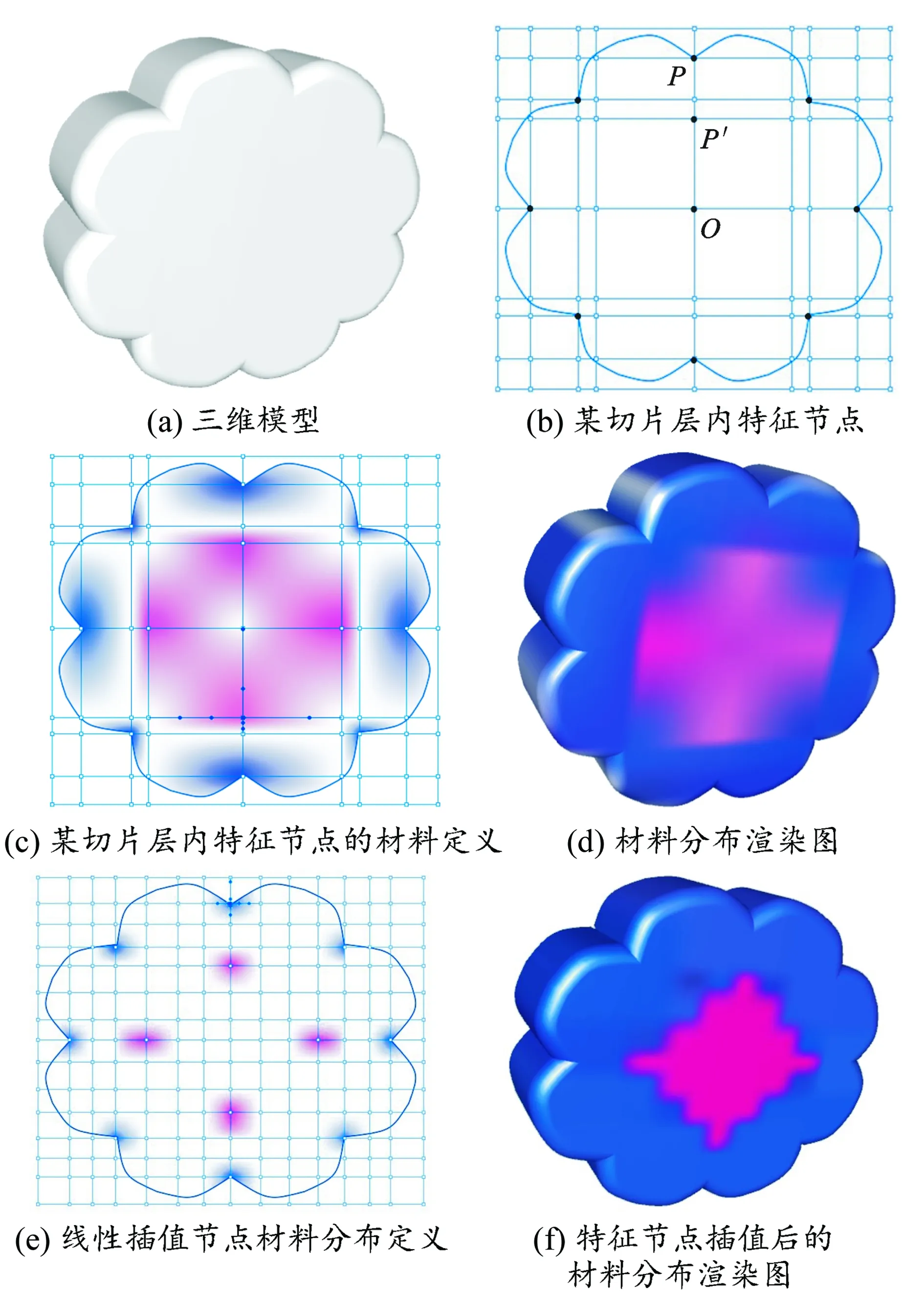
图7 异质零件的材料分布定义
由于每个零件的特征节点数量相对于空间点云数据集而言,只占极小比例,因此仅根据已定义的特征节点直接进行材料插值计算,获得的整个三维模型的材料分布的精确度将较低。为提高材料描述的精确度,结合已有的空间点云数据集,选定某一切片层,基于特征节点对模型进行线性插值,即可得到该切片层内细化后节点,如图7(e)所示。图7(e)、(f)所示为特征节点插值后的材料分布定义及其渲染图,对比图7(c)、(d),可看出特征节点插值后的材料分布的精确度大为提高。
根据上述各切片层内的材料定义过程,遍历各切片层,即可完成三维异质零件模型的材料定义。
4 异质零件材料分布表示方法
4.1 STL面片色彩信息映射的插值算法
使用色彩表示材料进行可视化设计。对于非两相梯度功能材料零件,或多于两相的梯度功能材料零件,三角面片内的色彩过渡与计算可采用双线性插值平均值法。
三角面片内任一点Pm的色彩值如图8所示,计算公式为
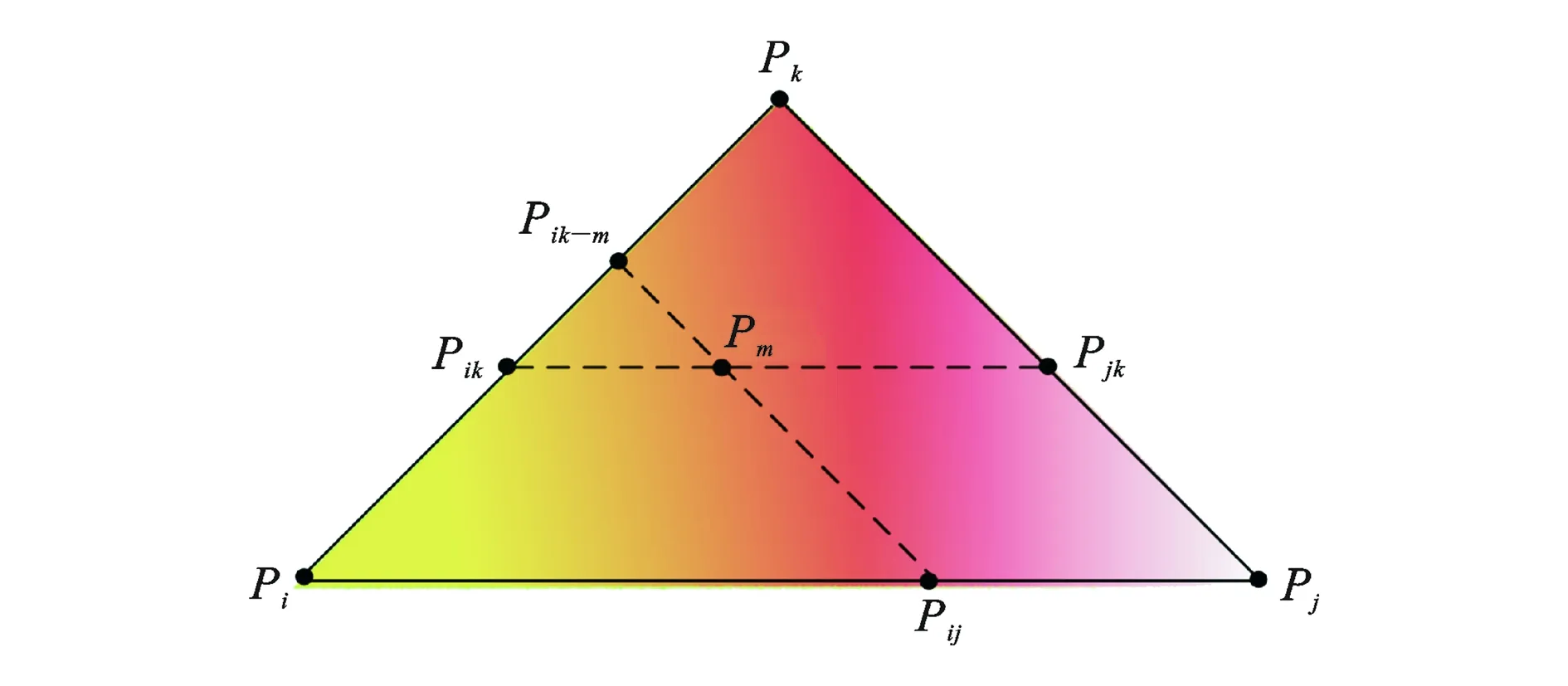
图8 任一点Pm的色彩值
(7)
式中:d(·,·) 为三角面片内任意两空间点之间的欧氏距离;α为点Pi与点Pjk的材料值之间的线性插值权重;β为点Pj与点Pik的材料值之间的线性插值权重;γ为点Pk与点Pij的材料值之间的线性插值权重。
对于两相梯度功能材料零件的可视化色彩填充,式(7)可简化为
(8)
位于填充线Pij-1Pik-1和Pij-nPik-n之间的区域为色彩过渡区域,如图9 所示,该区域内任一点Pm的色彩值为
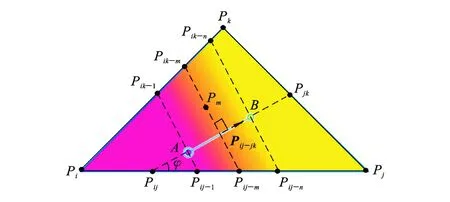
图9 插值运算
(9)
式中:α为点A色彩值和点B色彩值,也即Pij-1(或Pik-1)与点Pij-n(或Pik-n)的色彩值之间的线性插值权重。
色彩填充原则如下。
1)沿着线AB填充,A为起点,B为终点,直线簇Pij-mPik-m(1≤m≤n)为一组填充平行线,通过该组平行线与三角面片的交点,可得出任一点的色彩分量,从而为材料的对应关系奠定基础。
2)色彩填充沿着纯色种子A至B的色彩填充方向AB向量,即沿Pij-jk进行填充。
3)在填充线Pij-1Pik-1(即经过纯色种子的起点A的填充线)左侧的区域为纯色区域,该区域的色彩值与点A的相同;在填充线Pij-nPik-n右侧的区域亦为纯色区域,该区域的色彩值与B点的相同。
如果色彩沿着一个方向变化,则可简化为如图10所示的方向,图中A点为Pi点,B点为Pj点。也可离散为如图11所示的5个子面片,这就是面片细化,细化的原则:纯色种子A、B位置为顶点,AB连线为一条边,形成5个面片,仍继续使用色彩填充方向AB向量即Pij-jk进行填充。多相梯度功能材料细化可以得到更精确的材料模型。
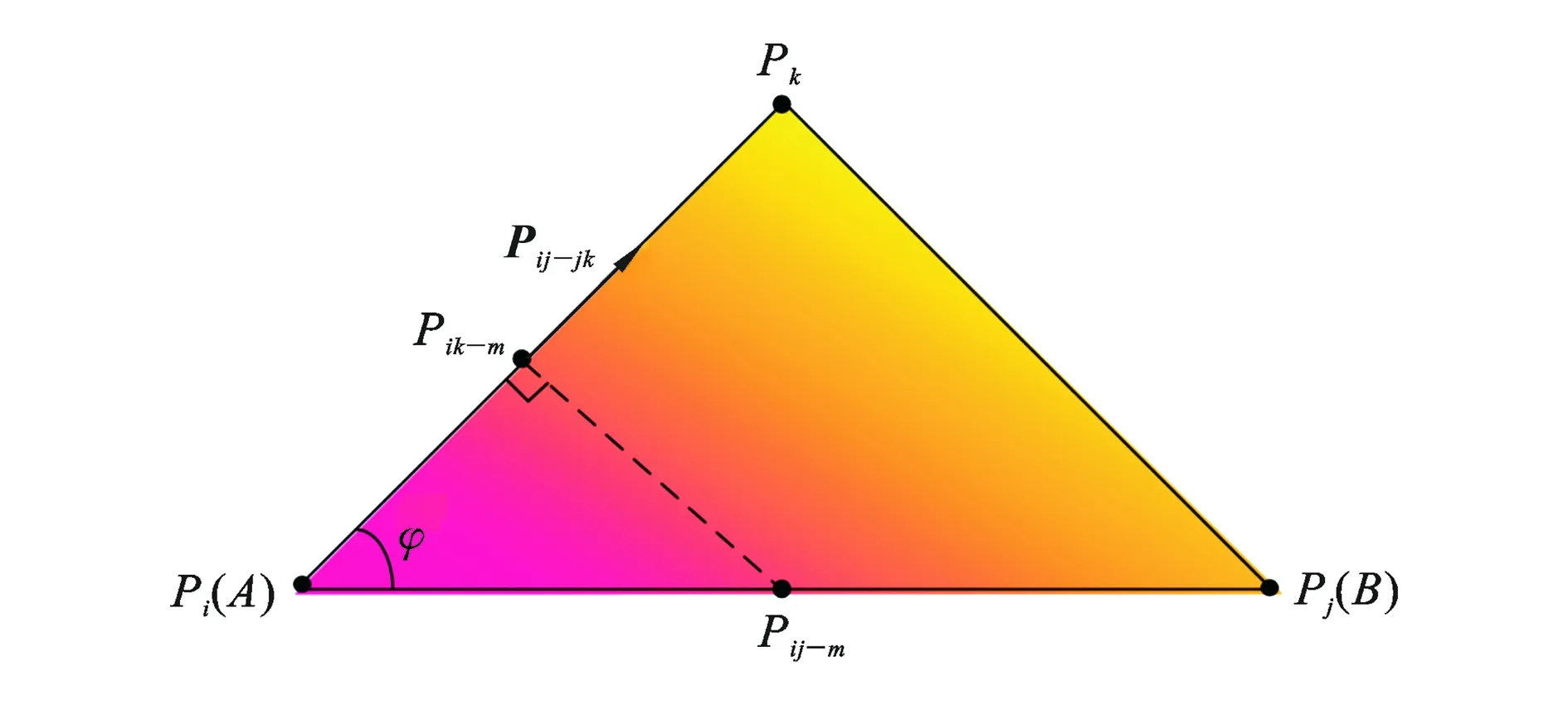
图10 简化色彩填充
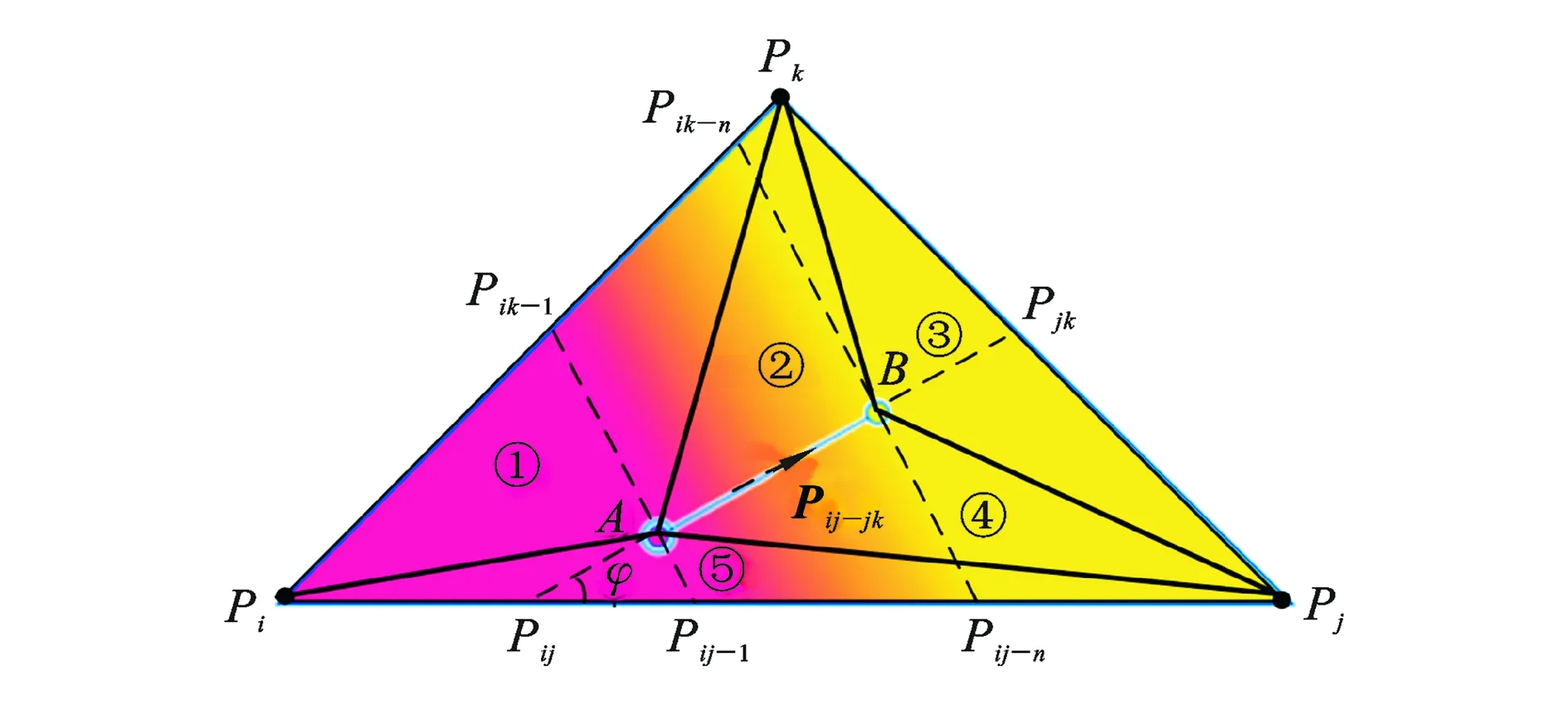
图11 片面细化
材料模型可以通过定义几个参数来设计:材料种类、材料特性、材料分布。其中材料分布最为复杂,可以采用材料分布函数来描述。可视化建模过程使用颜色代表不同材料,对单色STL模型进行三角面片上色、零件上色、窗口上色、壳体上色等,从而生成彩色STL模型。图12所示的是对一个单色STL模型进行处理后,得到的零件表面彩色STL模型,异质零件的3种材料按梯度分布。

图12 3种材料按梯度分布的异质零件
4.2 微四面体实体描述方法
每个微四面体基本单元由4个顶点、面法向量表示(见图13),因此每个微四面体也可以由4个具有三维空间坐标信息和法向量信息的顶点来表示。基于此,实体模型可由具有一定分布规律的点云数据来构造(见图14)。此处的点云数据与逆向工程(VE)中的点云数据有所不同,逆向工程所获得或使用的点云数据仅含有空间坐标信息,不含有法向量信息。由于点云数据的每个点均含有坐标信息和法向量信息,因此用此实体表述方法可在实体模型和点云数据之间实现互逆,从而为模型设计和模型可视化构建了一个桥梁。
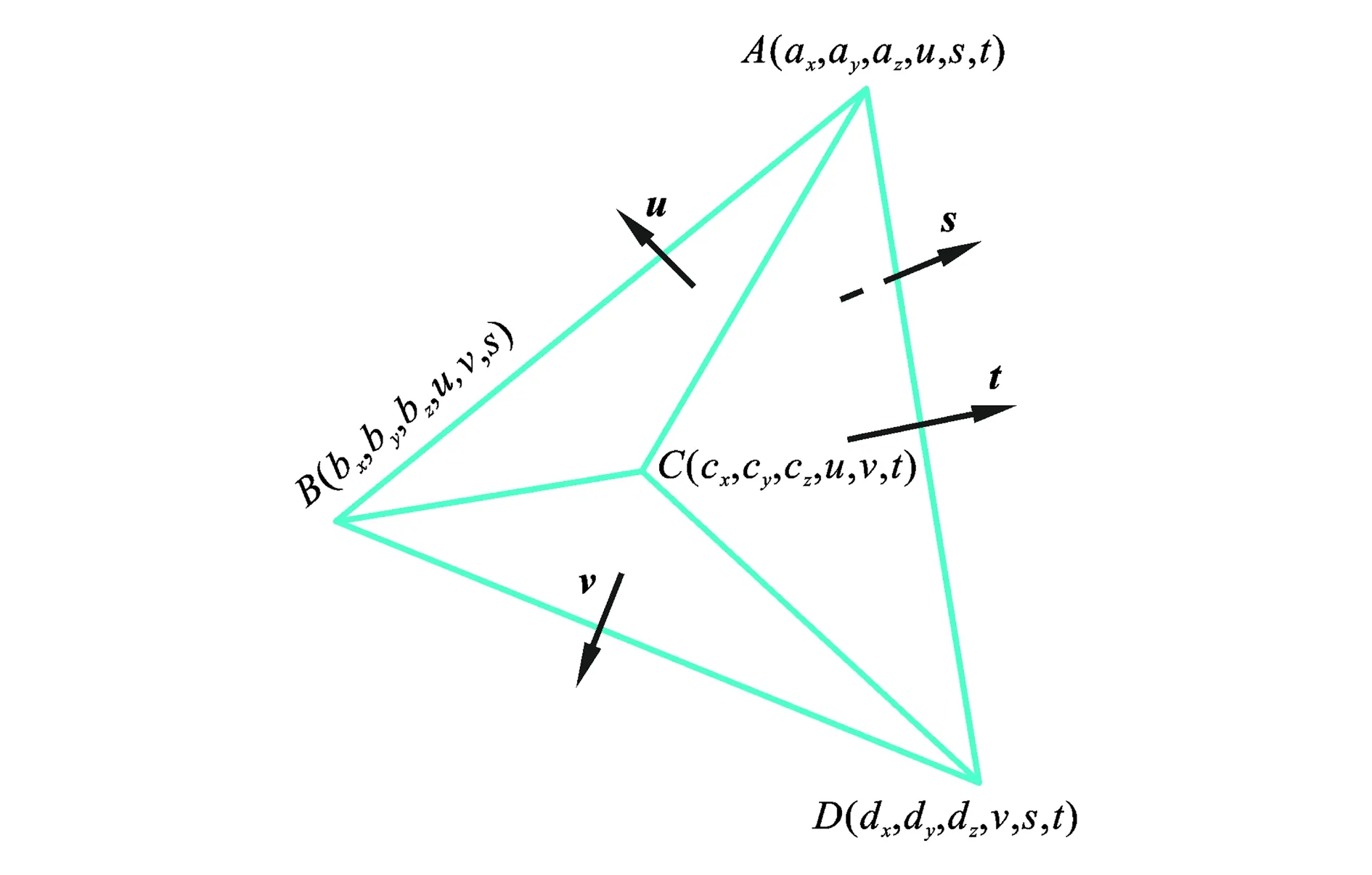
图13 微四面体示意图
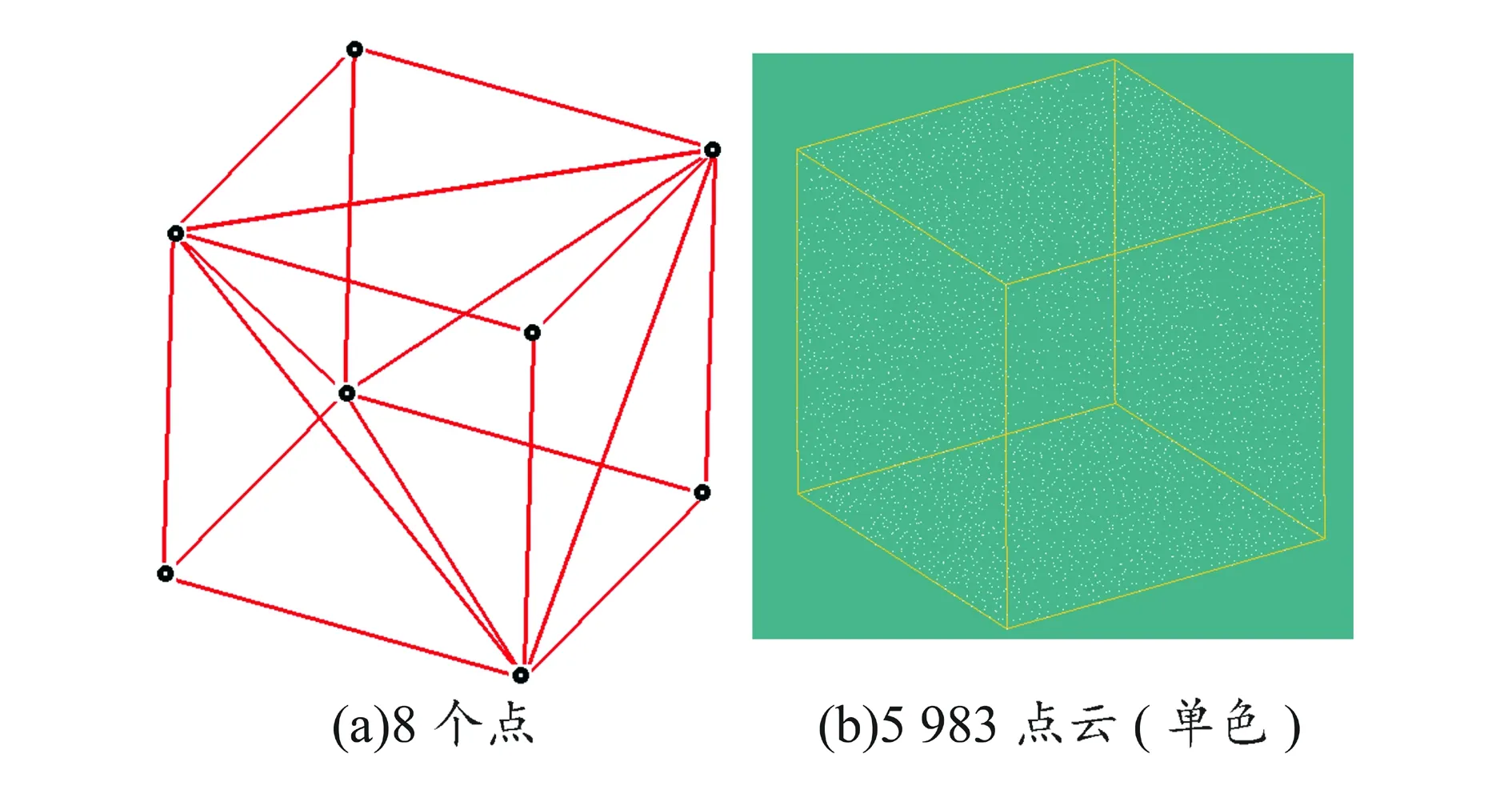
图14 实体的点云模型
构建基于微四面体空间单元的多相材料零件实体模型,每个微四面体可视为相对独立的实体单元,并赋予每个实体单元材料信息,如图15(b)所示的是图15(a)的爆炸图,每个微四面体均含有不同的材料信息,每个微四面体内部则可看作均质材料。
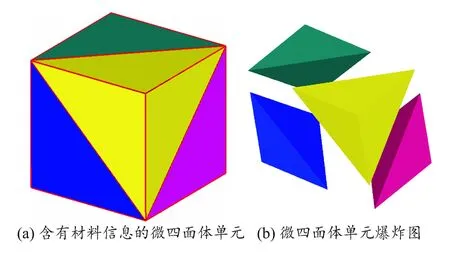
图15 基于微四面体单元的多相材料零件建模方法
鉴于异质零件的材料分布极其复杂,通过一个或一组分布函数来统一描述所有的异质零件的材料分布显然是极其困难的。因此,可采用基于STL均匀面片和点云数据相结合的方式,将整个异质零件的材料设计离散成每个微四面体(即三棱锥)的材料设计,通过定义点云中的各个点(也即微四面体的顶点)的材料分布来实现异质零件的材料设计,该方法的优点如下。
1)便于异质零件的CAD设计:STL格式是3D打印领域的准标准,具有极其广泛的应用,为各类快速成形系统所接受;采用STL格式作为异质零件的设计文件格式,有利于与各类商用CAD软件(如Pro/Engineer、UG、SolidWorks等)、3D打印成形设备和工艺对接。
2)便于异质零件的可视化:在STL模型的基础上,添加各面片的彩色信息以形成彩色STL模型;考虑到只是零件表面的可视化,因此只对异质零件位于表面的各STL面片进行色彩处理,而忽略各微四面体的其他三面的处理,可以节省大量的色彩处理时间。
3)便于异质零件的数据存储。
4)便于异质零件的成形加工。
5)微四面体内的材料分布是按照其4个顶点的各材料值递进分布的,可表示为材料分布函数,该函数中的参数有材料种类数、材料变化趋势(或称材料变化角度)、材料初始值和终点值。
4.3 改进的网格细化法
第3节的方法对梯度变化均匀、规律的异质零件能够很好地实现三维几何形状及材料分布的可视化,但对于具有不规则材料分布的实体,该方法有着明显的缺陷。如图16(b)、(c)所示,若简单采用第3节的方法,由于三角面片内部采用双线性插值算法,在三角面片各边长di(i=1,2,3)差异很大的情况下,双线性插值算法将不可避免地引入突变的视觉效应(即非连续、非渐进的材料分布),使得原有的模型材料分布无法得以正确表达。造成这种现象的主要原因是该方法中单元网格的离散化仍基于传统的均质三维实体处理方法,其离散依据是实体的几何约束(如曲面的曲率等),因而会产生极大、极小或狭长的三角面片。

图16 基于几何约束的曲面网格细化与视觉突变效应
为解决材料变化的视觉突变效应,在异质零件曲面的离散化过程中,应同时兼顾待渲染实体的几何约束和材料分布约束。一种简单的解决方法是通过网格细化来控制离散网格单元面片质量。如图17(a)所示,采用网格细化方法使得插值的原始场量(材料组分)变化局限于空间的局部邻域,可有效地解决材料变化的突变效应问题,实体模型如图18所示。
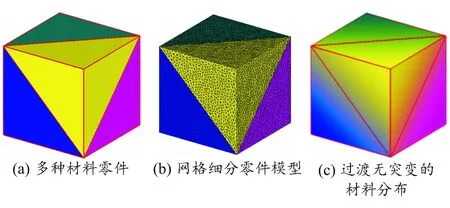
图18 减小突变效应的三维实体模型
5 结束语
基于体素法的设计是把异质实体的材料设计离散成每个微四面体(即三棱锥)的材料设计,通过定义点云中各个点(微四面体的顶点)的材料分布来实现异质零件的材料设计,该方法的优点如下:
1)便于异质零件的CAD设计。采用STL格式作为异质零件的设计文件格式,有利于与各类商用CAD软件和3D打印成形设备与工艺对接。
2)便于异质零件的可视化。
3)便于异质零件的数据存储。
4)便于异质零件的成形加工。
静态模型无法表达内部结构复杂和非匀质结构的对象,而本文微四面体内的材料分布是按照其4 个顶点的各材料值递进的,不但适合静态模型,也可以用于动态模型。
