矩阵转置对图形变换的几何意义*

曹富军，袁冬芳

(内蒙古科技大学 理学院，内蒙古 包头 014010)

转置是矩阵的一种运算，在矩阵的所有运算法则中占有重要地位.在线性代数[1，2]、多维图像和信号处理中，矩阵转置是最基本的操作，很多矩阵计算均需要矩阵转置操作，矩阵转置操作效率在较大程度上决定了科学计算和图形图像应用程序的性能[3，4].矩阵转置是矩阵的一种特殊变换，它有许多丰富的结果和应用[5，6]，文章通过设计案例揭示矩阵转置对图形变换的几何意义.

1 矩阵转置的定义

定义：设矩阵A=(aij)m×n，将矩阵A的行换为同序数的列所得到的矩阵称为A的转置矩阵，记作AT.

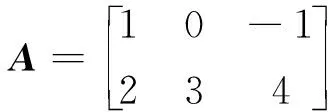
不妨沿着矩阵A和AT的第一行第一列元素a11右下方45°做一条射线，可得如下2个矩阵：

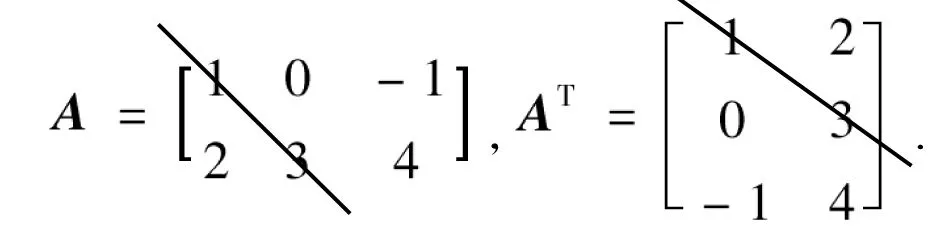
不难看出，AT实际上是由矩阵A沿着通过a11右下方射线作镜面翻转得到的,这也可以看作是矩阵转置的几何定义.

2 矩阵转置的几何意义

定义如下5×5的矩阵A根据矩阵转置的定义，很容易得到AT.

首先，由于矩阵A是方阵，将矩阵A的元素沿对角线进行分割，可以看出AT实际上是将中A所有元素沿主对角线进行镜面翻转得到的.

进一步，假设用1表示白色，0表示黑色，则矩阵A及AT的灰度图像如图1所示.

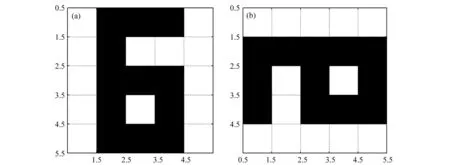
图1 矩阵A及AT的灰度图像(a)矩阵A的灰度图像；(b)矩阵AT的灰度图像

将矩阵A的灰度图像沿主对角线分割为上、下三角两部分，如图2(a)和(b)所示.分别将矩阵A的灰度图像的上、下三角部分做镜面翻转，如图3，4所示.由图3和4可知，矩阵AT的灰度图像也是将矩阵A的灰度图像沿着主对角线进行镜面翻转得到的.

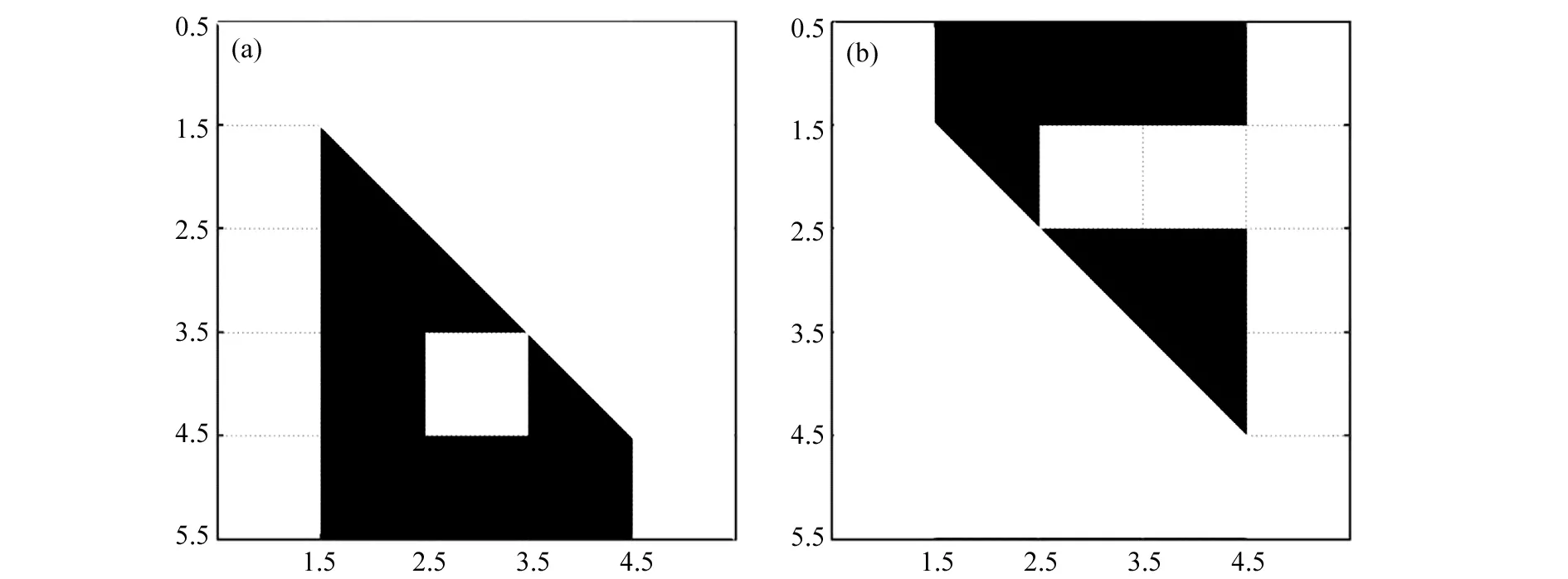
图2 矩阵A的灰度图像沿主对角线分割图(a)矩阵A灰度图像的下三角部分；(b)矩阵A灰度图像的上三角部分

图3 矩阵A的灰度图像的下三角部分沿主对角线做镜面翻转(a)矩阵A灰度图像的下三角部分；(b)图(a)沿主对角线做镜面反转图像

图4 矩阵A的灰度图像的上三角部分沿主对角线做镜面翻转(a)矩阵A灰度图像的上三角部分；(b)图(a)沿主对角线做镜面反转图像

为进一步探索矩阵A及AT的关系，对灰度图像做旋转变换，让其顺时针旋转90°，可得图5(b).

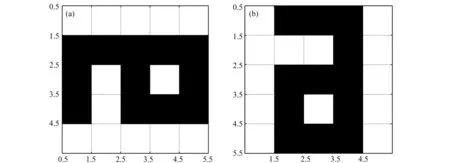
图5 矩阵AT的灰度图像及将其旋转90°后的图像(a)矩阵A的灰度图像；(b)矩阵A的图像顺时针旋转90°的图像

将矩阵AT的图像、矩阵AT的灰度图像顺时针旋转90°后的图像，以及矩阵A的灰度图像进行比较，如图6所示.由图6可知，矩阵A的灰度图像是由矩阵AT的灰度图像顺时针旋转90°后，再将所得图像沿y轴中心线作镜面翻转得到的.因此，可以得出如下结论，矩阵转置对图形变换的几何意义是先将图形沿y轴中心线做水平镜面翻转，再将所得图形逆时针旋转90°.

图6 对矩阵A，AT的灰度图像进行比较

考察2幅实际图片，选定一幅灰度图像图7(a)，其对应矩阵为A，将该矩阵AT转置后所表示的灰度图像图7(b)与原图像对比，进一步验证上述图形变换的规律.

图7 原始图像及将其对应矩阵转置后对应的灰度图像(a)测试矩阵A的灰度图像；(b)所对应的灰度图像

通过观察发现，将矩阵A进行转置得到AT，同时矩阵所对应的灰度图像将通过2个步骤发生变化如图8所示.①首先图像沿着中心y轴中心线做水平镜面翻转；②将翻转后的图像沿着逆时针旋转90°.这和通过数字矩阵的灰度图像得出的图形变化规律是一致的.

图8 矩阵转置对图像变换的2个步骤

3 结论

从矩阵转置的代数定义出发，首先阐释了矩阵转置直观上的几何定义.同时利用数字矩阵与灰度图像的对应关系，设计案例验证了矩阵转置直观几何定义的准确性.进一步通过观察矩阵转置后灰度图像的形式，总结出了矩阵转置对图形变换的几何意义，即矩阵转置对应着先将原图形沿着y轴中心线做水平镜面翻转，接着将翻转后的图像沿逆时针旋转90°.最后通过实际图像进一步验证了该规律的准确性.