铝合金超静定矩形薄壁梁的刚度理论研究与数值计算

徐志强，任毅斌，刘云刚，胡国强，宋小雨

（中铝材料应用研究院有限公司，北京102209）

0 前言

薄壁梁结构作为客车结构的主要承力部件，在车身结构中有着十分重要的作用，会影响整车的力学性能，因此研究薄壁梁的刚度对提高整车的性能有着非常重要的意义[1-3]。

一般在客车中采用的薄壁梁多为矩形梁[4]，因此，本文将从理论及有限元两方面分析矩形薄壁梁结构的截面几何参数和材料特性对其弯曲和扭转刚度的影响，并通过算例对不同壁厚铝合金矩形薄壁梁的抗弯及抗扭刚度进行理论及数值计算，得出理论与数值相同的计算结果。

1 薄壁矩形梁的刚度理论计算

考虑到薄壁梁在客车上的设计，梁的两端均会与其他的部件有机械连接或者焊接，因此，在单独分析薄壁梁时，可假定薄壁梁两端固支，研究在两端固支的约束条件下梁上任意一点的刚度值。

1.1 抗弯刚度理论计算

一长度为L的两端固支梁如图1所示，在距左端x处受一垂向载荷P作用。

由平衡方程知

式中，FAX、FAY、FCX、FCY分别为A、C点的X、Y向的支座反力；MA、MC分别为A、C点的弯矩。

公式中（1）含有6个未知数，而平衡方程只有3个，因此多出3个约束，属于三次超静定问题。要求解上述问题，需要变形协调方程。由于该梁为两端固支，固支梁的两端挠度与转角均为0，即：

由公式（1）、（2）可得

其中，ωB为B点的挠度。

B点的挠度可以通过对上述固支梁进行转化解得，即上述固支梁转变为将A点固支，C点的约束采用MC和FCY等效，则B点处的挠度可以看作分别受到P、MC、FCY以后叠加在一起，即

其中，ωP为载荷P在B点产生的挠度，ωMC为弯矩MC在B点产生的挠度，ωFCY为载荷FCY在B点产生的挠度，其值由材料力学可知[5-6]：

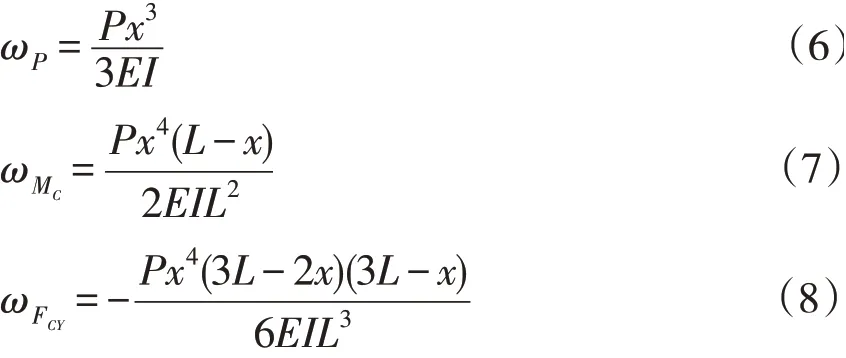
式中，E、I分别为材料的弹性模量及截面对x轴的惯性矩。

将公式（6）、（7）、（8）同时代入到公式（5）中，可得

将式（9）代入公式（4），可得B点的抗弯刚度为：

对于矩形薄壁梁，如图2所示，其抗弯刚度同样可以用公式（12）来表示。

图2 矩形薄壁断面

其中矩形梁的惯性矩为：

其中，b，h分别为薄壁梁截面厚度t中线处的宽和高。

将公式（12）代入公式（11），可得矩形薄壁梁的抗弯刚度为：

1.2 扭转刚度理论计算

考虑AC梁两端固支，如下图所示，假定AC梁的剪切模量为G，对轴心的惯性矩为Iρ。

由静力学平衡方程可知：

公式（15）中含有2个未知数，而平衡方程只有1个，多出1个约束，属于一次超静定问题，因此要求解上述问题，需要变形协调方程。由于该梁为两端固支，固支梁AC的扭转角为0，即：

将AC梁看成AB段和BC段，AB段扭矩为TA，BC段扭矩为TC，AC的扭转角等于AB与BC扭转角之和，即

由于AB段的扭转方向和BC段的扭转方向相反，对于任意闭口薄截面杆件，如图4所示。

图4 任意闭口薄壁断面

根据扭转角的计算公式[6]，则有AB段与BC段的扭转角分别为

式中，s为中线长度，t为壁厚，A为断面中线所围成的面积。

将公式（18）代入公式（17），可得：

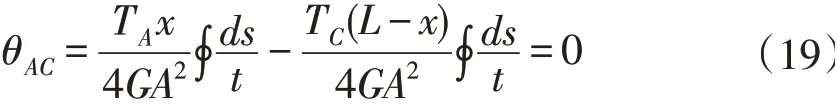
联立公式（15）、（19），可得：

则梁AC上一点B处的扭转角为：

因此，梁AC上受力点B处的扭转刚度等于B处的扭矩除以B处的扭转角，即：

对于图2所示的等壁厚矩形薄壁梁，则：

将公式（23）、（24）代入到公式（21）、（22）中，可得受力点B处的扭转角及扭转刚度，即：

2 算例

设置一算例，假定一长度L=1 000 mm的矩形薄壁梁，中线宽度b=60 mm，中线高度h=100 mm，壁厚为t，t取1~9 mm中的整数，矩形薄壁梁材料为铝合金，其弹性模量为70 GPa，密度为2 700 kg/m3，泊松比为0.33。

2.1 铝合金矩形薄壁梁的抗弯刚度

为了所得到的抗弯刚度具有普遍性，矩形薄壁梁所受载荷不施加在梁的中间位置，设定矩形薄壁梁在x=400 mm处受到P=100 kN的载荷，两端固定。

2.1.1 理论计算

将上述已知条件代入到公式（13）中，可得出在受力点处的弯曲挠度及抗弯刚度值KC，具体值见于表1。

2.1.2 有限元数值计算

采用一维梁单元进行建模，单元尺寸设置为10 mm，按照上述条件设置梁的截面参数，在两端施加全约束，并在x=400 mm处施加P=100 kN的集中载荷，如图5所示。

图5 弯曲有限元模型

通过计算可得出在受力点处的位移UY，如图6所示。而抗弯刚度值可由下列方程式求得。

图6 不同壁厚受力点处的位移云图

式中，KBI为数值计算抗弯刚度。将不同厚度的矩形薄壁梁计算出的位移及抗弯刚度列于表1。

表1 矩形薄壁梁弯曲的理论及数值解

从表1可以看出，通过理论计算得出的抗弯刚度与通过有限元数值计算得出的抗弯刚度完全一致，从而验证了抗弯刚度的理论计算公式的有效性。

2.2 矩形薄壁梁的抗扭刚度

同矩形薄壁梁的抗弯刚度：设定矩形薄壁梁在x=400 mm处受到T=100 kN·mm的扭矩，梁的两端固定。

2.2.1 理论计算

将上述已知条件代入到公式（26）中，可得出在受力点处的扭转刚度值KT，具体值见表2。

2.1.2 有限元数值计算

采用三维实体单元进行建模，按照上述条件设置梁的截面参数，在两端施加全约束，并在x=400 mm处施加T=100 kN·mm的扭矩，如图7所示。

图7 扭转有限元模型

通过数值计算，得出各厚度的位移云图，如图8所示。而扭转刚度为：

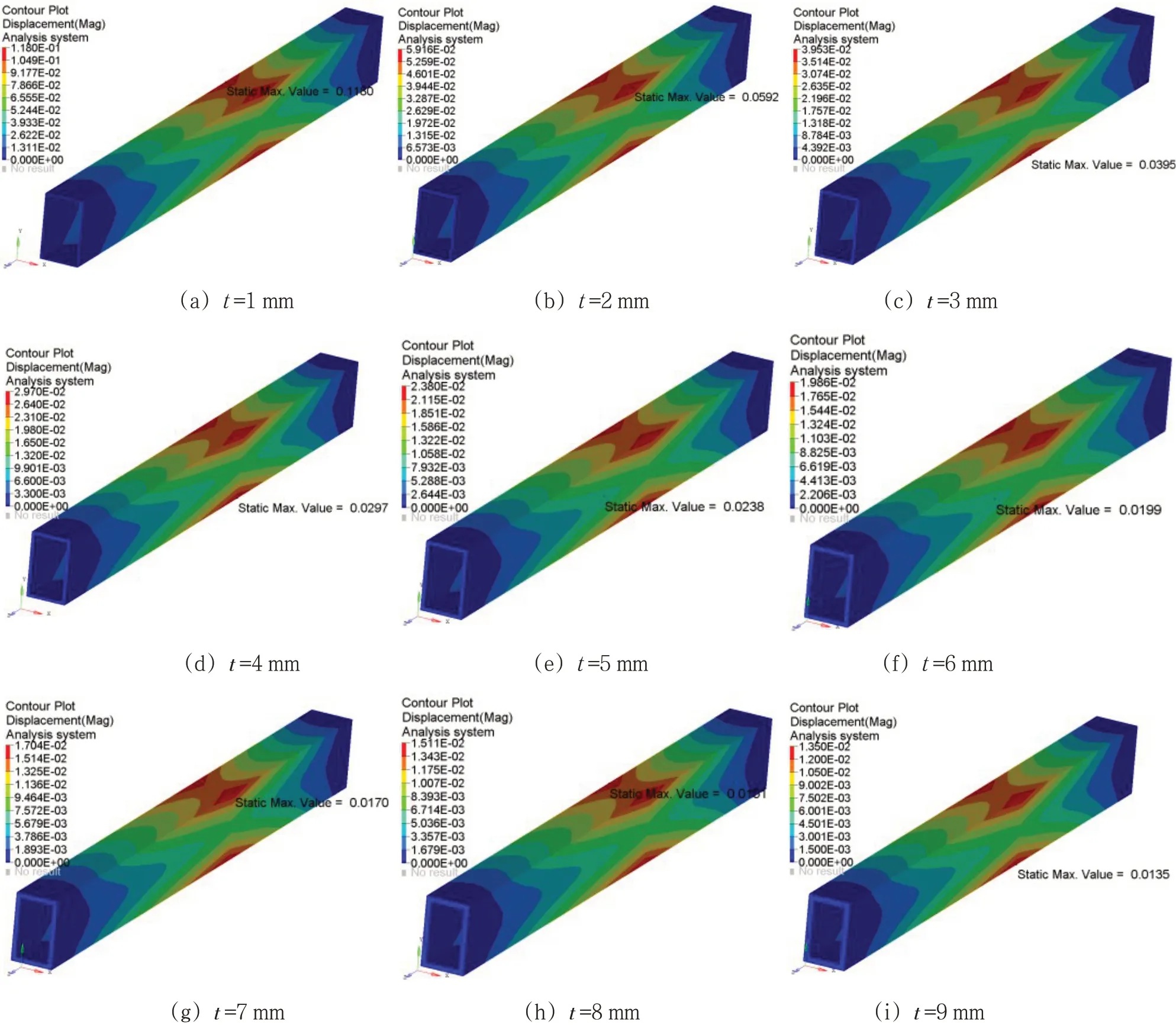
图8 不同壁厚的位移云图

式中，θTI为在受力截面处的扭转角，KTI为数值计算出的扭转刚度。

θTI可通过选取中间截面上沿轴心对称的节点相对位移除以两者距离得到[7]，然后将计算出的扭转角代入到公式（28），可得到不同厚度铝合金矩形薄壁梁的扭转刚度，见表2。

表2 矩形薄壁梁扭转的理论及数值解

从表2可以看出，通过理论计算得出的抗扭刚度与通过有限元数值计算得出的抗扭刚度完全一致，从而验证了抗扭刚度的理论计算公式。

3 结论

对两端固支的任意截面梁进行了弯曲及扭转的理论研究，对加载处的抗弯刚度及抗扭刚度进行了理论推导，并以铝合金矩形薄壁梁作为算例，对其抗弯刚度及抗扭刚度进行了理论与数值计算，结论如下：

（1）通过理论研究，得出了两端固支的任意截面梁在受力处的抗弯刚度计算公式，并通过该理论公式推出了铝合金薄壁矩形截面梁的抗弯刚度计算公式。

（2）通过理论推导得出了任意闭口截面梁在两端固支的情况下其受力处的抗扭刚度的计算公式，该理论计算公式适用于任意闭口截面梁。然后通过该理论计算公式推出了薄壁矩形截面梁在加载处的抗扭刚度。

（3）通过算例，在两端固支的铝合金矩形薄壁梁400 mm处位置进行加载，对不同厚度的薄壁矩形梁的抗弯刚度及扭转刚度进行了理论及数值计算。计算结果表明，对不同厚度的薄壁矩形梁，其抗弯刚度及抗扭刚度理论值与数值计算值保持一致，从而验证了抗弯及抗扭刚度的理论计算公式的有效性，为客车的矩形梁设计提供了一定的基础。