高温高电流密度下BGA焊点电迁移损伤

2021-11-17文廷玉马立民王乙舒王娇娇

北京工业大学学报 2021年11期

郭福，文廷玉，马立民，王乙舒，王娇娇

(北京工业大学材料与制造学部，北京 100124)

近几年我国新能源汽车行业不断发展，汽车电子产品集成化明显提高，汽车及发动机系统微处理器规模不断增大，供电系统电压由12 V提升至42 V.同时汽车芯片的封装形式也从四周无引脚封装形式向球栅阵列封装(ball grid array，BGA)和细间距球阵列封装方向发展，封装密度不断提高.位于引擎、排气管和燃烧室附近的汽车电子器件还要经受150 ℃的温度考验，这对车载电子器件的封装可靠性提出了更高的要求[1-4].

电子封装结构中的焊点主要起到了保证芯片与基板的电气互连和机械支撑的作用[5].当流过焊点内部的电流密度超过104A/cm2时，焊点内部的原子将会在电子风力的作用下产生移动，导致电迁移损伤空洞的产生.伴随损伤的不断扩大，器件最终将发生断裂失效，所以解析原子在焊点内部的迁移规律对研究BGA焊点电迁移损伤有至关重要的意义.

研究者提出了在电流密度作用下原子的迁移通量Jem[6-7]和在焦耳热作用下产生的热扩散通量Jth[8].由于封装体中不同材料的热膨胀系数不同，在温度发生变化时，材料界面之间会产生应力，故有基于热应力的应力扩散通量Js[9]，且

(1)

(2)

(3)

式中：Z*为净有效电荷数；e为电子电荷；ρr为材料的电阻率；j为施加的电流密度；c为扩散原子浓度；D为原子在基体中的扩散系数；kB为玻尔兹曼常数；T为绝对温度；Q为传递的热量；Ω为扩散原子的体积；σ为应力；x为距离.

但是对于极端工况下扩散过程的解析，通常很难用实验的方法来完成，国内外已有一些利用有限元计算方法来分析BGA焊点电迁移的研究.Dalleau等[10]和Liu等[11]利用原子通量散度法计算了电迁移、热迁移、应力迁移下各原子通量散度和焊点内部原子浓度，并利用生死网格法对电迁移损伤进行模拟.但是Dandu等[12]指出该方法依赖于单元网格密度，一些情况下无法准确预测电迁移缺陷位置，且没有考虑焊点自身原子浓度梯度的影响.梁利华等[13]对原子通量散度法进一步修正，提出包含焊点自身原子密度梯度的原子密度积分法，并对芯片级封装结构进行计算，其结果与实验基本一致，证明了焊点原子梯度通量在原子扩散中有一定的作用，同时该团队还发现电迁移寿命随有效电荷数绝对值的增大而减小，随着材料扩散激活能的增大而增大[14].电迁移的发生并不是电流的单独作用，而是电场、温度场、应力场以及物质扩散场多场耦合的结果.

因此本文建立了BGA封装体在高温、高电流密度下进行电迁移的数学模型，利用COMSOL Multiphysics 5.5的系数形式偏微分方程接口完成原子扩散模拟，并利用域常微分和微分代数方程接口完成电迁移损伤的动态记录过程.考虑了焊点在高温下的黏塑性行为，采用非线性的Anand本构关系分析焊点的力学特征，模拟接近真实的服役过程.

1 有限元建模

1.1 几何模型与网格划分

本文以COMSOL Multiphysics 5.5软件为工具进行仿真工作，分析在高温且通电时BGA焊点内部原子的迁移现象.为了突出主要研究问题，减少计算量并提高运算收敛性，本研究设计了由36个(6×6)直径为300 μm的焊球，并将其连接成菊花链(daisy chain)结构，主要包含的结构为：Sn3.0Ag0.5Cu焊球、Cu导线、FR-4上下树脂基板，忽略了尺寸较薄的阻焊层和塑封在环氧塑封料内部的薄层Si芯片，所有界面完全接触且不考虑封装结构水汽、缺陷、材料辐射温度等影响.BGA器件几何模型如图1所示.几何结构的各参数为：下侧基板L1=5 500 μm、L2=5 000 μm、H1=1 200 μm；上侧基板L3=3 500 μm、H2=1 000 μm；焊球D1=300 μm、D2=500 μm、H3=200 μm；导线D3=800 μm；电极D4=600 μm.

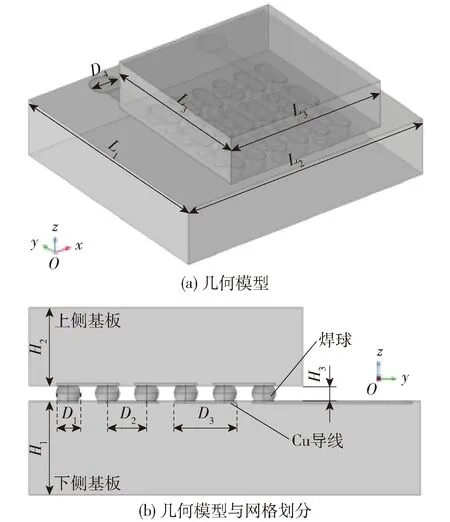
图1 BGA器件几何模型Fig.1 Model for BGA

为了保证网格连续性采用了用户控制场网格：BGA焊球以及上、下侧基板为自由四面体网格，铜导线为自由四边形映射网格，铜导线与上、下侧基板过渡位置为金字塔网格，网格尺寸为细化，且依据几何尺寸适当控制网格的大小和分布.网格划分后的BGA器件几何模型如图2所示，在几何尺寸较小处网格密度较高，在Cu导线和基板之间做到了良好的网格过渡，保证了各部分材料之间的耦合关系.

图2 BGA结构网格划分Fig.2 Computational grid of BGA model

1.2 数值模拟方法及边界条件

为了分析BGA封装结构电迁移动态过程，建立了电场-热场-应力场-浓度场4个物理场的耦合模型，研究电迁移过程中的原子扩散通量-原子浓度-损伤比例之间的关系.计算流程如图3所示.

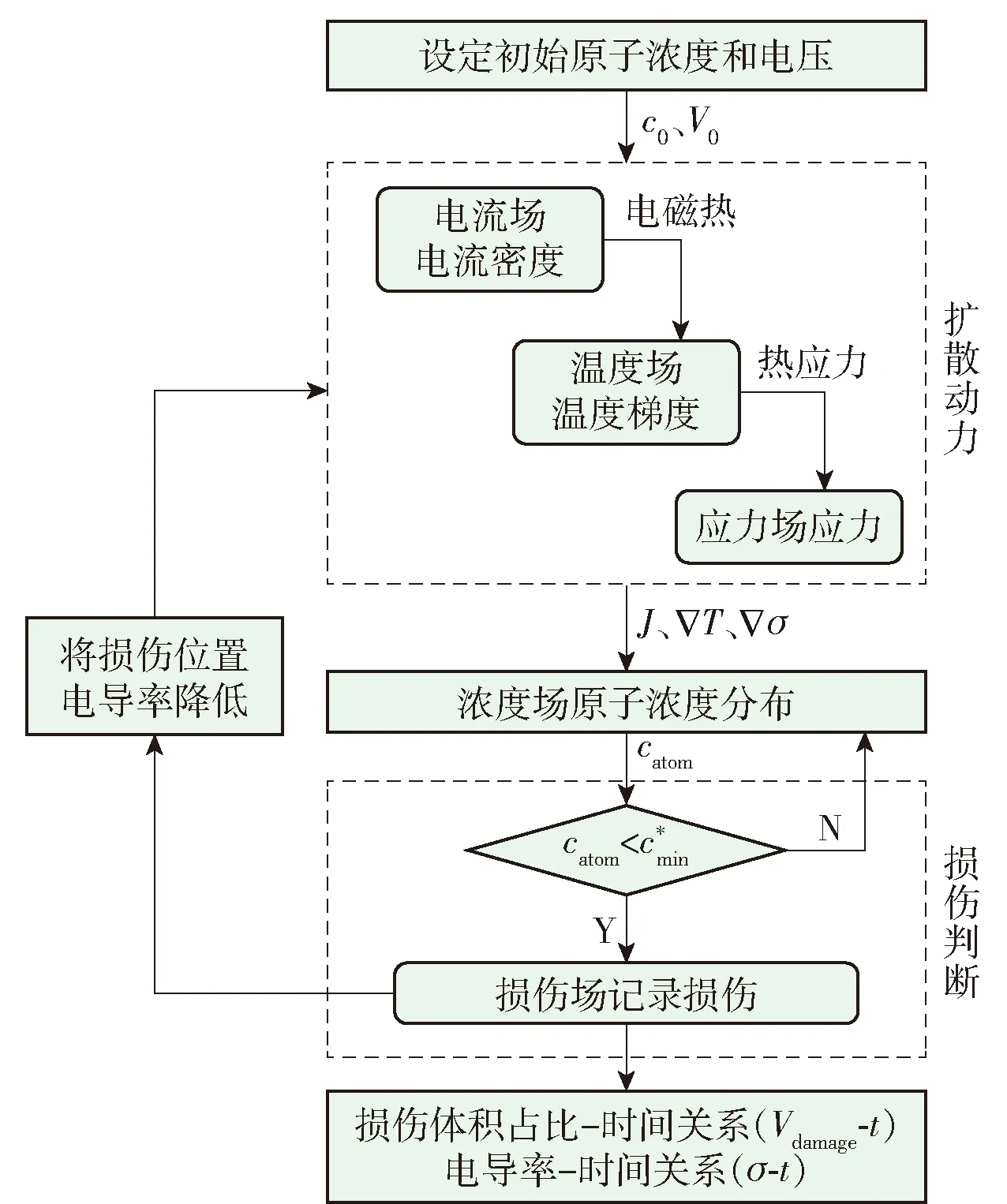
图3 电迁移空洞演化分析流程Fig.3 Procedure for EM damage evolution

1.2.1 物理场控制方程

电流场的宏观分析主要利用麦克斯韦方程组和电流守恒求解.

(4)

(5)

温度场主要基于能量守恒公式

(6)

式中：第1项为温度积累；第2项为固体热传导；第3项为热对流；T为温度；t为时间；ρm为材料的密度；Cp为热容；k为导热系数；u为流体速度；Q为热量.

固体力学场则由平衡方程、本构方程和几何方程来描述.本构方程主要描述材料的线弹性力学特征，其中εth为热应变矩阵，由热应力式(10)决定，εcr为蠕变应变矩阵，由黏塑性过程决定.几何方程保证材料在发生变形后保持连续体的条件.

(7)

S=C∶[ε-(εth+εcr)]

(8)

(9)

εth=α(T-Tref)

(10)

式中：ρ为密度；u为位移张量；t为时间；S为应力张量；f为体积力张量；C为刚度矩阵；ε为总应变矩阵；α为热膨胀系数.其中材料的刚度矩阵为对称矩阵，Cij=Cji，对于各向同性材料，仅存在2个独立变量C11、C44，C11为杨氏模量E；C44为剪切模量G.

浓度场应满足质量守恒原理

(11)

式中：q为总原子通量.原子通量在本研究中由电子风力通量qem、热梯度通量qth、应力梯度通量qs、原子梯度通量qc构成，即

q=qem+qth+qs+qc

(12)

(13)

1.2.2 对不可逆损伤的构建

电迁移空洞演化分析流程中，损伤判断是基于域常微分和微分代数方程接口来实现的.当焊点内部出现损伤时，损伤部位的电导率将被降至一极小值.现实情况下这种改变是不可逆的，但由于模拟中可能存在损伤部位原子浓度先降低后增大的情况，故需要在原子浓度与电导率之间引入一状态量Ddam来记录损伤状态，避免可逆过程的发生.COMSOL Multiphysics 5.5中预置的方程形式为

(14)

该研究中不包含变量u的偏导项，ea=da=0，故可表示为

f=Ddam-N(if(Ddam(catom)>Ddam,
Ddam(catom),Ddam))

(15)

整理后得到损伤Ddam的表达式为

Ddam=N(if(Ddam(catom)>Ddam,
Ddam(catom),Ddam))

(16)

式中：N()表示对括号内的部分取Jacobian矩阵；if(a,b,c)语句所表达的含义为如果满足条件a则输出结果b，否则输出结果c，则Ddam始终取得最大值.Ddam(catom)为原子浓度对损伤的影响，且

(17)

根据

(18)

则电导率σ可始终保持在一较小值，实现损伤记录的动态模拟过程.

1.2.3 边界条件

在电流加载过程中，FR-4为一电绝缘材料，在Cu导线和BGA焊点上施加电场.在热传导过程中，焦耳热Qe作为内部边界条件的热源输入，而外部边界条件主要受到边界方程的控制

(19)

式中：n为边界法向；q0为边界处热通量.当外部边界热绝缘时q0=0；当存在器件和环境的热对流时，采用牛顿冷却定律来进行边界热对流过程的约束，即

q0=h(Text-T)

(20)

式中：h为换热系数.在FR-4表面和BGA焊球表面设置对流热通量起到和周围环境换热的作用，并设定环境温度Text=150 ℃.上、下侧基板的对流换热系数h1=25 W/(m2·K)，BGA与四周换热的对流换热系数h2=7 W/(m2·K).

由于器件被固定在某一平面上，将上侧基板上表面和下侧基板下表面设定固定约束，即

ux=uy=uz=0

(21)

本研究中，原子扩散只考虑发生在BGA焊点内部，故在BGA焊球边界上的原子通量为0，满足

q·n=0

(22)

1.3 材料属性

材料所需要的参数主要由所选定的物理场所决定，如表1、2[15-19]所示.固体力学模块中的材料包括线弹性材料FR-4、Cu，黏塑性材料Sn3.0Ag0.5Cu，其黏塑性模型为Anand模型，流动方程和演化方程分别为

表1 浓度场Sn3.0Ag0.5Cu材料属性Table 1 Sn3.0Ag0.5Cu property for concentration field

(23)

(24)

(25)

式中：A为黏塑性率系数；Q为活化能；ξ为应力乘子；m为应力灵敏度；为变形阻力饱和系数；s0为变形阻力初始值；h0为硬化常数；a为硬化灵敏度；n为变形阻力灵敏度，具体数值如表3所示.

表2 电流场、温度场、应力场材料属性Table 2 Materials property for electric,heat,and stress field

表3 Anand模型参数Table 3 Viscoplastic parameters for Anand

2 计算结果及分析

2.1 末态原子浓度及初始物理状态分析

通电336 h后的原子浓度分布如图4所示.可以发现，BGA焊点内部原子浓度变化主要集中在与Cu基板接触的界面处.在电流输入、输出端，原子浓度有明显升高和降低的趋势.原子浓度最低点出现在C2焊点上，为0.71 mol/m3；最高点出现在D2号焊点上，为1.43 mol/m3.

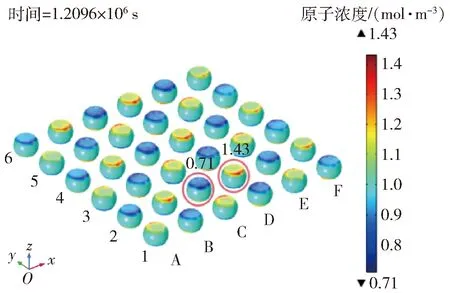
图4 通电336 h焊点内部原子浓度分布Fig.4 Distribution of atom concentration in solder joints for 336 h

取末态原子浓度最低的C2焊点进行进一步分析，图5(a)所示为电子运动方向，电流在焊点内部分布不均匀，在电流输入端和输出端出现了电流密度的拥挤效应，最大电流密度可达2.5×104A/cm2，所以电迁移首先发生在电子流入端.由于焦耳热与电流密度的平方呈正比，故电流密度大的地方温度越高.由于焊点C2位于器件内侧，整体温度较高，焊点顶部与底部的温差较小，最大温度梯度仅3 640 K/m，远小于温度梯度阈值105K/m.根据模拟结果，焊点的应力水平在10～20 MPa，应力梯度最大值为7 310 MPa/m.

图5 焊点C2初始原子扩散动力云图Fig.5 Contour of electromigration driving force on C2

2.2 电迁移过程中焊点浓度分析

图6明确了焊点内部原子浓度在0～336 h随时间的变化趋势.假设初始原子浓度为1 mol/m3，原子在各种动力下持续从焊点的阴极向阳极运动，其过程主要可以分为3个阶段：在0～69 h内原子主要沿电子移动方向迁移，阳极电子流出处原子积累；在69～126 h内随着原子在阳极侧不断堆积，阳极侧原子横向迁移，形成堆积小丘；在126～336 h内阴极原子沿着界面横向迁移，空洞不断扩展.由于恒定高温且通风条件良好的通电环境难于搭建，故在模拟前期进行了室温下BGA焊点电迁移的实验.如图7所示，在通电600 h后阳极界面金属间化合物层由3.2 μm增厚至3.4 μm，阴极侧的电子流入处出现细小空洞[20-21]，虽然实验是在常温下进行，损伤积累较为缓慢，但模拟结果与实验现象基本一致.

图6 焊点C2不同时间下原子浓度分布Fig.6 Contour of atom concentration at different current stressing time

如图8所示，取C2焊点的4个顶点Q1～Q4，其中Q1是电子流入端，Q4是电子流出端.由图9可以看出，Q1、Q2原子浓度不断降低，Q3、Q4原子浓度不断升高.Q1原子浓度在111 h前由于电流堆积效应的不断增大，其下降速率不断加快，随着损伤的不断积累浓度变化趋于平稳，Q2点主要以原子的横向迁移为主，开始阶段原子浓度变化相对缓慢，而在后期损伤阶段加快.Q3、Q4位于阳极侧，以原子堆积形成小丘为主要失效形式，但随着小丘的不断形成，原子浓度增大速率持续减小，且Q3的变化相对滞后，如图9、10所示.

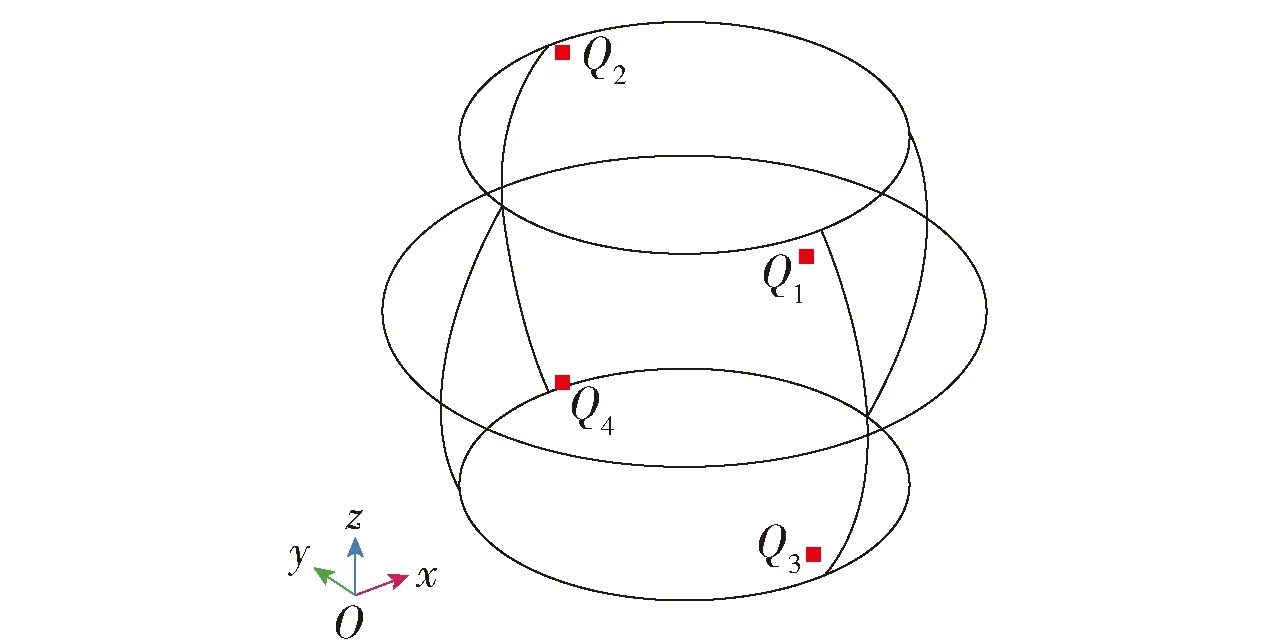
图8 Q1～Q4 位置Fig.8 Q1-Q4 locations on solder joint

图9 原子浓度-时间关系曲线Fig.9 Atom concentration-time curve

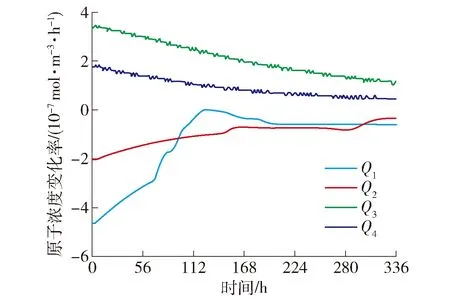
图10 原子浓度变化率Fig.10 Atom concentration rate-time curve

2.3 电迁移过程中焊点扩散通量分析

图11为Q1～Q4位置的电子风力通量Jem、热梯度通量Jth、应力梯度通量Js、原子浓度梯度通量Jc随时间的变化关系，其中Jem和Jc在10-12mol/(m3·s)数量级，而Js、Jth分别为10-15mol/(m3·s)、10-16mol/(m3·s)数量级，Js、Jth对电迁移贡献较小.在电迁移的初始阶段主要以Jem为主要动力，Q1处于电子流出端附近，随着空洞的形成在其周围出现了电流密度的激增，故111 h前Jem增大，当损伤产生后趋近于0，Q2由于距离Q1处较远其Jem作用时间延长.而在焊点阳极侧始终存在Jem的作用，由于Q4为电子流出端，故其附近的Jem大于Q3处.由于原子由阴极向阳极不断堆积，在电迁移后期Jc随时间不断增大，Jc在Q4处远大于Q1处，Jc对电迁移起到了一定的抑制作用，因此阳极侧原子浓度升高的速率在不断减慢.

图11 焊点C2原子通量-时间关系Fig.11 Atom flux-time curve of solder joint C2

2.4 阴极空洞对原子迁移的影响

Zhang等[22]提出随着电迁移空洞的不断形成，电子会在新的损伤周围重新形成堆积，造成电流密度集中的现象，本节通过动态模拟的方法对该过程进行研究.如图12(a)所示，随着通电时间的延长，在20 h时空洞开始形成，56 h后空洞开始扩展，空洞在20～167 h内在电迁移的作用下呈加速扩展状态，222 h后扩展速率明显降低.随着空洞体积的不断累积，焊点C2的-z方向上的平均电导率在不断降低，由8.69×106S/m降低至8.02×106S/m，电导率的下降限制了电子沿-z方向大范围的迁移，但其局部迁移可能加剧.由图12(c)可以看到，随着通电时间的延长，焊点上的最大电流密度在不断增大且电流塞积因子也在同步增大，导致焊点内局部区域的温度、电流密度升高，进一步促进了该处的原子迁移.图12(d)为1.2、88.0、178.0和336.0 h焊点C2上Q1Q4对角线上的电流密度分布，随着电迁移过程的进行，电子流出端的缺陷长度不断增加，同时其周围的电流密度不断增大.

2.5 环境温度对原子迁移的影响

本节研究了恒定环境温度以及热循环条件对BGA焊点内原子迁移的影响.

取h1=h2=30 W/(m2·K)，设置环境温度为25、75和150 ℃.图13为焊点内最低原子浓度随时间的变化规律，当环境温度为25 ℃时，在电迁移336 h后焊点最低原子浓度基本不发生变化而150 ℃则出现明显的降低.计算发现，随着温度的不断升高，焊点的平均原子扩散系数分别为9.488×10-19、1.210×10-17和6.412×10-17m2/s，25 ℃时平均原子扩散系数比75 ℃、150 ℃小2个数量级，故在常温时电迁移作用下的原子扩散十分缓慢.

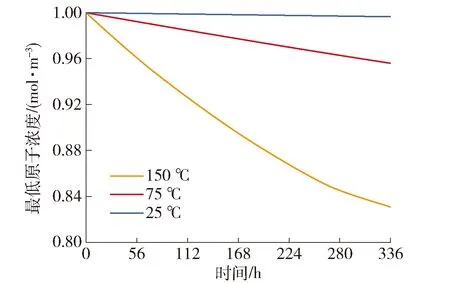
图13 不同环境温度下最低原子浓度-时间曲线Fig.13 Minimum of atom concentration under different ambient temperatures

图14为环境温度循环条件下前5周期最低原子浓度曲线，其浓度下降阶段出现在高温保温阶段，而在低温保温阶段则没有明显变化.对热扩散系数的研究发现，在高温阶段焊点的热扩散系数平均值为6×10-19m2/s，而在低温阶段基本接近于0，随温度表现出周期性变化.因此，温度对焊点热扩散系数的影响较大.

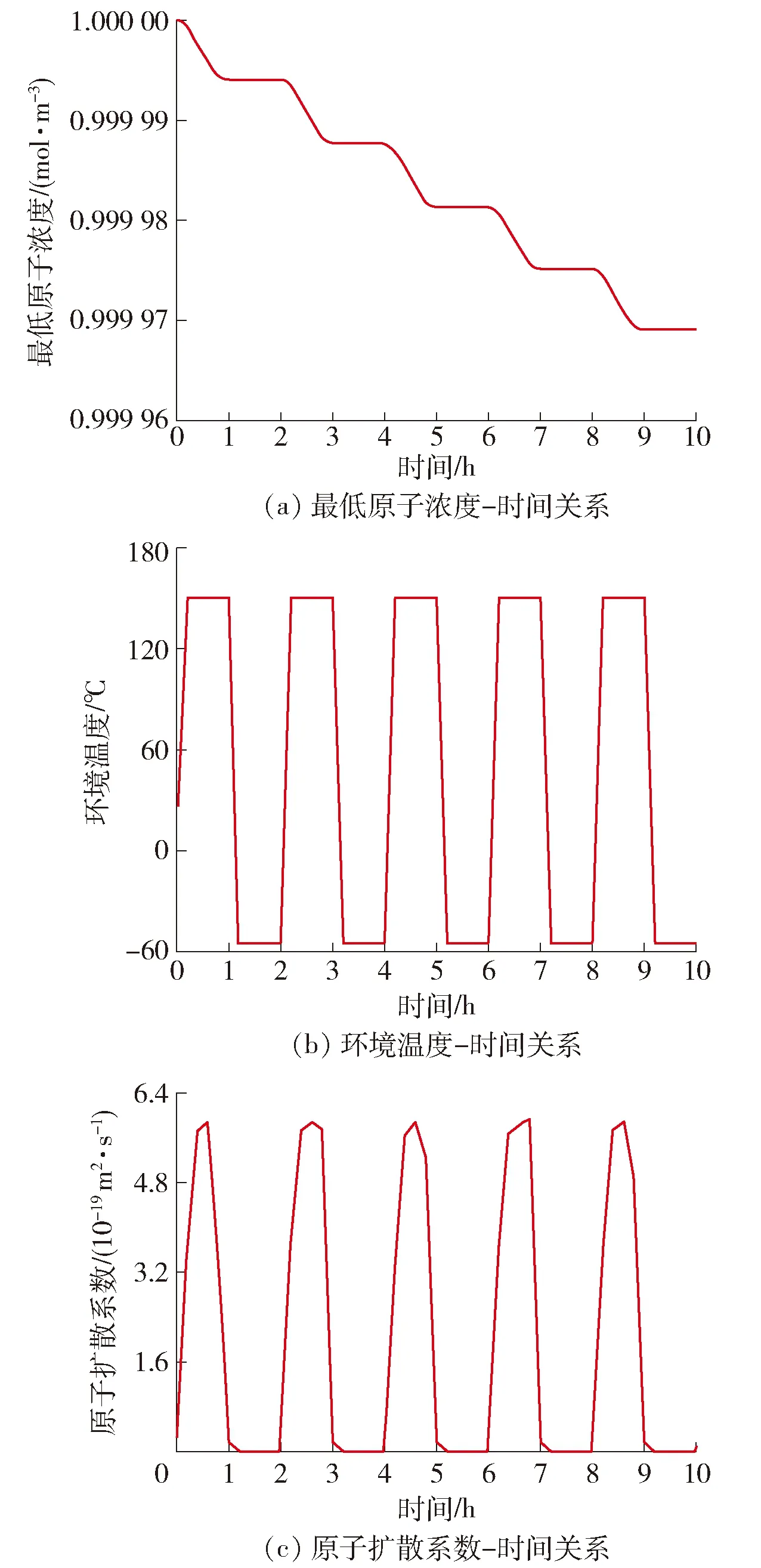
图14 温度循环条件下前5周期的原子扩散Fig.14 Atom diffusion behavior under thermal cycle condition for the first 5 cycles

图15为原子浓度最低点前5周期内原子扩散通量随时间变化的曲线.可以看出，在环境处于低温时4个通量均接近0，在高温时Jem为10-15mol/(m2·s)、Js为10-16mol/(m2·s)、Jth和Jc为10-19mol/(m2·s)数量级.与高温状态下相同的是Jth对电迁移贡献并不大，Jc随时间不断增大.但与高温状态下不同的是Js与Jem相差不大，在高低温循环过程中在焊点边界处形成较大的应力梯度达1.37×105MPa/m，使得Js也成为原子扩散的主要动力之一.