移动无线物联网感知层传感控制定位算法研究

冯志江，司亚超，冯 帆

(1. 河北建筑工程学院，河北 张家口 075000；2. 河北工业大学，天津 300401)

1 引言

物联网是互联网以及因特网的基础上扩展的，它是各种信息感知设备与互联网相结合形成的庞大网络，可以实现任何时间、任何地点、任何人员、任何机器、任何事物的互相连通，是20世纪发展起来的新型。它作用于工业、医疗、农业、交通、环保、消防等各个方面，与生活紧密相连，为人们带来了各种便利[1]。

物联网层次结构分为三层，分别为应用层、网络层和感知层，作为核心的感知层是信息采集的关键部分[2-4]。WSN(Wireless Sensor Networks，无线传感器网络)是物联网感知层的关键技术[5-6]，在监测区域内部署了大量的微型传感器节点，通过无线通信形成了一个多跳自组织网络系统，其中节点定位技术是该系统的重要技术之一，它是一种基于网络中几个位置已知的节点，也称为锚节点，需要通过某种定位机制来确定其它位置未知的节点的过程[7-8]。

节点定位是当前研究的热点问题，目前许多相关领域都有涉及，如莫建麟，研究面向LoRa网络的基于维纳滤波的RSSI定位算法[9]，该种算法测距存在噪声，且定位精度不高；尹烨佳等，研究非视距环境中的无线网络残差加权定位算法[10]，该种算法计算较为复杂，效率较低；施涛涛等，研究基于支持向量机的混合相似度室内指纹定位算法[11]，该种算法参考点匹配精度和数据利用率较低。

为解决目前研究算法存在的问题，本文提出基于跳数修正的DV-hop定位算法，实现移动无线物联网感知层传感控制定位，其在DV-hop定位算法的基础上，通过对锚节点间跳数，以及未知节点到锚节点间跳数进行修正，从而提高了定位精度和效率，以便更好地应用于实际中。

2 移动无线物联网感知层传感控制定位方法

2.1 DV-hop定位算法

DV-hop算法主要通过跳计数和距离向量来估计未知节点到信标节点的距离，未知节点的位置信息可以通过三边或者多边测量法得到，图1描述了其方法过程[12]。

图1 DV-hop算法过程

从图1中可以看出，包含于未知节点通信区域中的信标节点数量并不多，节点到其通信区域外的多个信标节点的距离信息可通过上述方法得到

以下三个阶段是DV-hop算法的主要组成部分：

第一阶段：网络中全部节点的信标节点最小跳数值，可以根据典型的距离矢量路由协议得到。

第二阶段：使用信标节点对平均每跳距离值进行计算的时，若一个信标节点的坐标为(xi，yi)，其计算过程可以用式(1)描述

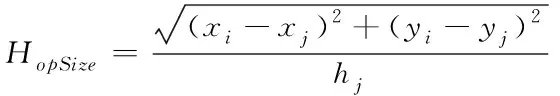
(1)

式中，信标节点j的坐标用(xj，yj)表示，信标节点j与信标节点i之间的最小跳数为hj；基于信标节点i计算出的平均每跳距离用HopSize表示。作为一个校正值的HopSize，广播可以使用可控泛洪法在传感器网络中进行，为了确保由最近的一个信标节点传送过来的内容为节点接收到的校正值，那么第一个校正值应该被传感器所保存，收到校正值后的未知节点到信标节点的距离可用跳数和校正值进行计算。

第三阶段：未知节点的坐标可采用最小二乘法进行计算，且要满足未知节点最少得到三个信标节点的距离的条件。Ri=(xi，yi)T，i=1，2，……，M，为给出的信标节点集，其中信标节点的数目为M，Li表示未知节点X=(x，y)T到信标节点i的最小跳数，所以可以用di=Li×HopSize表示未知节点X=(x，y)T到信标节点i的距离值，式(2)描述了未知节点X的坐标的计算过程

(2)

式(4)表示未知节点X的坐标，其根据标准的最小均方差估算方法得到：

X=Ri×HopSize

(3)

2.2 基于跳数修正的改进算法

根据上小结可得，传统DV-Hop定位算法在用公式Cphopspi对节点间跳数进行计算时，存在与实际距离偏离，从而导致节点定位有较大误差的问题，这是由于每跳的距离不同，但不论其在通信区域之中相距多远，都估算其跳数为一跳。以两锚节点间的最短路径为例验证上述问题，具体如图2所示。

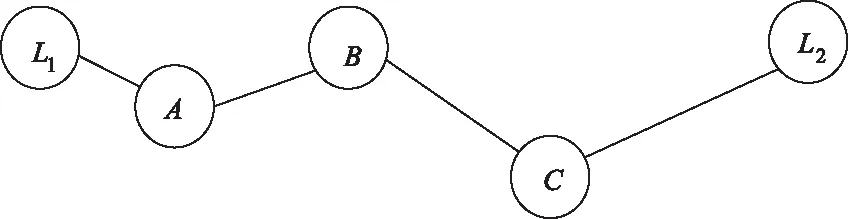
图2 两锚节点间的最短路径

如图2所示，L1和L2分别为两个锚节点，可以看出每跳的长度都不一样，要将和实际值接近的最后一跳的长度作为节点的通信半径，如果有较大的误差被引入到最后的定位中，则是因为根据传统DV-Hop定位算法对锚节点间的最小跳数进行计算时仍然记作4跳。

对于上述问题，为了减少由跳数引起的误差，提出了一种新的跳数计算方法，定义一些参数来说明本文的改进算法。

定义1：i和j分别表示两锚节点，R表示通信半径，理想跳数Hij为两锚节点间的实际距离和所有节点的通信半径的比，式(4)是其表达式

(4)

定义2：偏离因子αij为理想跳数和节点间实际跳数的相对误差，式(5)是其表达式

(5)

式内，两锚节点i和j之间的实际跳数值用hopsij表示。偏离理想跳数的程度可以根据偏离因子对节点间平均每一跳进行反映，当实际跳数与理想跳数的偏离程度越大，则此实际跳数替代理想跳数所引起的误差也越大。

定义3：如果用hopsij表示两锚节点i和j之间的实际跳数值，αij表示偏离因子，跳数修正系数wij可用式(6)表示

(6)

式内，n的取值范围为正整数，要想定位效果最佳，是在n=2的条件下，以下描述了跳数修正算法的具体过程。

2.2.1 锚节点间跳数

根据式(7)修正锚节点间跳数，可以尽量使实际跳数与理想值接近

(7)

式(8)是理想跳数和改进后的跳数间的偏差表达式

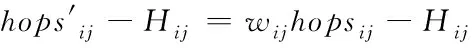
(8)

2.2.2 未知节点到锚节点间跳数的改进

传统DV-Hop定位算法里使用距离矢量交换协议，在未知节点对到锚节点的距离进行计算时，结果是一个整数跳数，但实际的跳数并非全是整数，因此，使用整数跳数来计算未知节点和各个锚点之间的距离肯定会有误差。为改善这个缺陷，修正未知节点和锚节点间的跳数。

①一个未知节点计算出距离它最近的锚点的跳数。

若p为未知节点，i为锚节点，其间的实际跳数用hopspi表示，n为锚节点数目，式(9)可用于修正其跳数，结果为

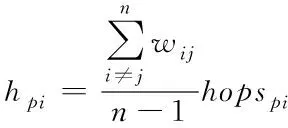
(9)

②未知节点对距其它锚节点的跳数进行计算。

式(10)可用于修正未知节点p对距其它锚节点的跳数的计算

hpj=wijhopspj

(10)

式内，由式(6)可获得wij，未知节点和其它锚节点之间的实际跳数用hopspj表示。为了更好地反映未知节点到其它锚节点的跳数偏离程度，可以使用两锚节点间的偏离因子，原因是大部分未知节点距离任意两锚节点的路径会出现部分重叠。

2.2.3 改进后的算法流程

以下是改进后的DV-Hop算法流程：

第1阶段：获取全部节点到各个锚节点的距离和跳数信息，和传统算法步骤一样。

第2阶段：首先锚节点间的跳数修正可以通过式(7)实现，接下来基于式(1)用修正的跳数对每个锚节点的平均每跳距离进行计算。

第3阶段：分别采用式(9)和式(10)用未知节点对距其最近锚节点与其它锚节点的跳数进行修正，接下来要计算距各个锚节点的距离，可以根据与其最近锚节点的平均每跳距离得到。最后未知节点的位置估算坐标，可在计算出的距离的基础上，根据二维双曲线定位算法获得。

3 实验分析

以采用MATLAB软件仿真的移动无线物联网感知层为实验对象，在100m×100m的正方形区域中随机分布了传感器节点，研究不同跳数修正系数、不同总节点个数、不同通信半径、不同锚节点比例以及不同偏离因子下，本文算法的控制定位效果。

3.1 不同跳数修正系数的控制定位误差

为了实现本文算法的移动无线物联网感知层最佳定位精度，统计不同跳数修正系数下，本文算法的定位误差，当跳数修正系数n分别为1、2、3、4时，本文算法定位误差随锚节点比例变化的结果如图3所示。

图3 不同跳数修正系数控制定位误差对比

分析图3可得，本文算法控制定位误差随着锚节点比例的增加而减小，并且逐渐趋向平稳，当跳数修正系数为2时的控制定位误差始终低于跳数修正系数为1、3和4的定位误差，说明跳数修正系数为2时，本文算法控制定位精度最高，所以本文算法在进行移动无线物联网感知层传感控制定位过程中，将2作为最佳跳数修正系数值。

3.2 不同总节点个数的控制定位误差

为了测试本文算法控制定位移动无线物联网感知层的精度，实验分析在不同总节点个数下本文算法的控制定位误差，并设计对比实验，选取文献[9]的面向LoRa网络的基于维纳滤波的RSSI定位算法、文献[10]的非视距环境中的无线网络残差加权定位算法以及文献[11]的支持向量机的混合相似度室内指纹定位算法，作为本文算法的对比算法，统计四种算法在不同总节点个数下的控制定位误差，结果如图4所示。

图4 不同总节点个数控制定位误差对比

分析图4可得，四种算法的控制定位误差都随着总节点个数的增加而减小，而在节点所在区域不变的情况下，随着节点总数的增加，则逐渐趋于稳定，移动无线物联网中节点密度增大，导致控制定位精度提高。相对于其它三种算法，本文算法在不同总节点个数下的控制定位误差始终保持最低，而文献[11]算法的控制定位误差始终保持最高。对比这些数据可以看出，在不同总节点个数下，本文算法具有较高的控制定位准确性和稳定性，可大大提高移动无线物联网感知层的控制定位效果。

3.3 不同节点通信半径的定位误差

实验分析在不同节点通信半径下不同算法的控制定位误差，结果如表1所示。

表1 不同节点通信半径下的控制定位误差对比(m)

通过对表1的分析，四种算法的控制定位误差均随节点通信半径的增加而增加，这是由于节点间跳数的增加以及节点间跳数的误差的增加所造成的。相对于其它三种算法，在同一通信半径下，本文算法的控制定位误差始终保持最低，说明本文算法控制定位移动无线物联网感知层的效果最好。

3.4 不同锚节点比例的定位误差

实验分析在不同锚节点比例下不同算法的控制定位误差，结果如图5所示。

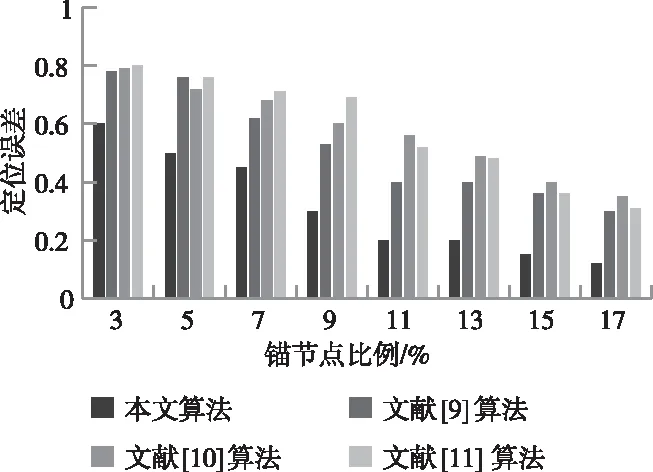
图5 不同锚节点比例控制定位误差对比

分析图5可得，四种算法的控制定位误差都随着锚节点比例的增大而减小，并逐渐趋向稳定。相对于其它三种算法，本文算法在不同锚节点比例下的控制定位误差始终保持最低，且与其它算法的控制定位误差值相距较大。对比这些数据可以看出，在不同锚节点比例下，本文算的控制定位准确性和稳定性最高，可通过选择较大的锚节点比例进一步提升移动物联网感知层传感控制定位效果。

3.5 不同偏离因子的控制定位误差

实验分析在不同偏离因子下不同算法的控制定位误差，结果如图6所示。

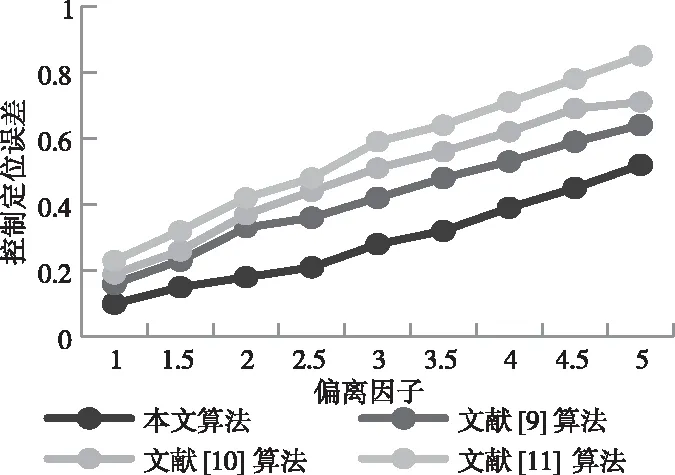
图6 不同偏离因子控制定位误差对比

分析图6可得，四种算法的控制定位误差都随着偏离因子的增大而增大。相对于其它三种算法，本文算法在不同偏离因子下的控制定位误差始终保持最低，当偏离因子为5时，本文算法控制定位误差不超过0.5，三种对比算法的控制定位误差均超过0.6。实验结果说明，不同偏离因子下本文算法具有较高的控制定位准确性，可选择较小的偏离因子，进一步提升移动无线物联网感知层控制定位精度。

4 结论

为实现移动无线物联网感知层传感控制定位，本文在传统DV-hop定位算法的基础上，提出基于跳数修正的DV-hop定位算法，实现移动物联网感知层传感控制定位，提升移动无线物联网感知层传感控制定位的准确性和稳定性，为生产和生活提供更加精确和科学的数据支持。日后，还可以进一步改善该研究算法，使其在各大领域中广泛应用普及，助我国迈入智慧时代的脚步更快更稳。