考虑恐慌特性的老年人疏散仿真研究

陈 晨，陆丽丽，曹祖平

(宁波大学海运学院，浙江 宁波 315211)

1 引言

安全问题一直是所有社会事业建设中极其重要的一个研究问题，每当发生如火灾，暴力袭击等突发状况时，总会给社会和个人家庭带来巨大的伤害和负面影响。

而应急疏散问题又属安全研究领域重要研究方向之一。目前为止，国内外对于应急疏散问题，主要采用理论建模后通过计算机仿真来获得人群疏散过程的典型现象并得到相关结论。其中常见的模型有社会力模型、磁场力模型、格子气模型和元胞自动机模型[1-5]，其中元胞自动机模型由于更新规则简单，模型易于拓展等优势在行人疏散研究中受到广泛应用。因此Burstedde等[6，7]基于元胞自动机的基础上，提出了传统地场元胞自动机模型，通过引入静态场和动态场分别反映行人对环境的熟悉程度和跟随效应；刘全平等[8]将多智能体与元胞自动机相结合，拓展了模型规则实现了个体差异化的研究；李阳[9]通过引入熟悉度参数，将动态场参数改进为基于距离选择的动态场，修正了行人转移概率; Ezaki等[10]则通过引入距离场的概念来描述行人疏散过程的聚集行为;周金旺、陆丽丽等[11，12]人分别在原有模型基础上对传统的地场元胞自动机模型进行拓展，提出了考虑结伴行为的疏散模型；熊立春[13]等人和陈长坤[14]等人采取问卷调查方式，分别研究了声光刺激对行人疏散时心理的影响和疏散心理及行为决策。

然而通过整理现有国内外研究成果发现，已有研究多是以正常人疏散为研究重点，而正常人与老年人混合疏散时，老年人的心里因素对群体疏散的影响研究较少。

随着中国老年化程度的加深，老年人群的疏散效率对安全影响也是越来越大，因此对此类人群的疏散研究十分必要，本文以地场元胞自动机为基础，以老年人为研究对象，建立了考虑恐慌心理的老年人群疏散模型，本文最后利用模型分析了不同群体密度下，老年人所占比例对群体疏散的影响，研究结果对老年人出入较多的公众场所的设计和流量控制具有实际意义。

2 老年人疏散特性提取

2.1 问卷调查

为了确保受访者的主体为目标年龄段人群，问卷采取线下调查方式，分别在宁波市江北区两个老旧小区进行了随机问卷调查。总计问卷调查178份。

2.2 数据统计

通过问卷收集，老年人疏散问卷统计数据见表1。

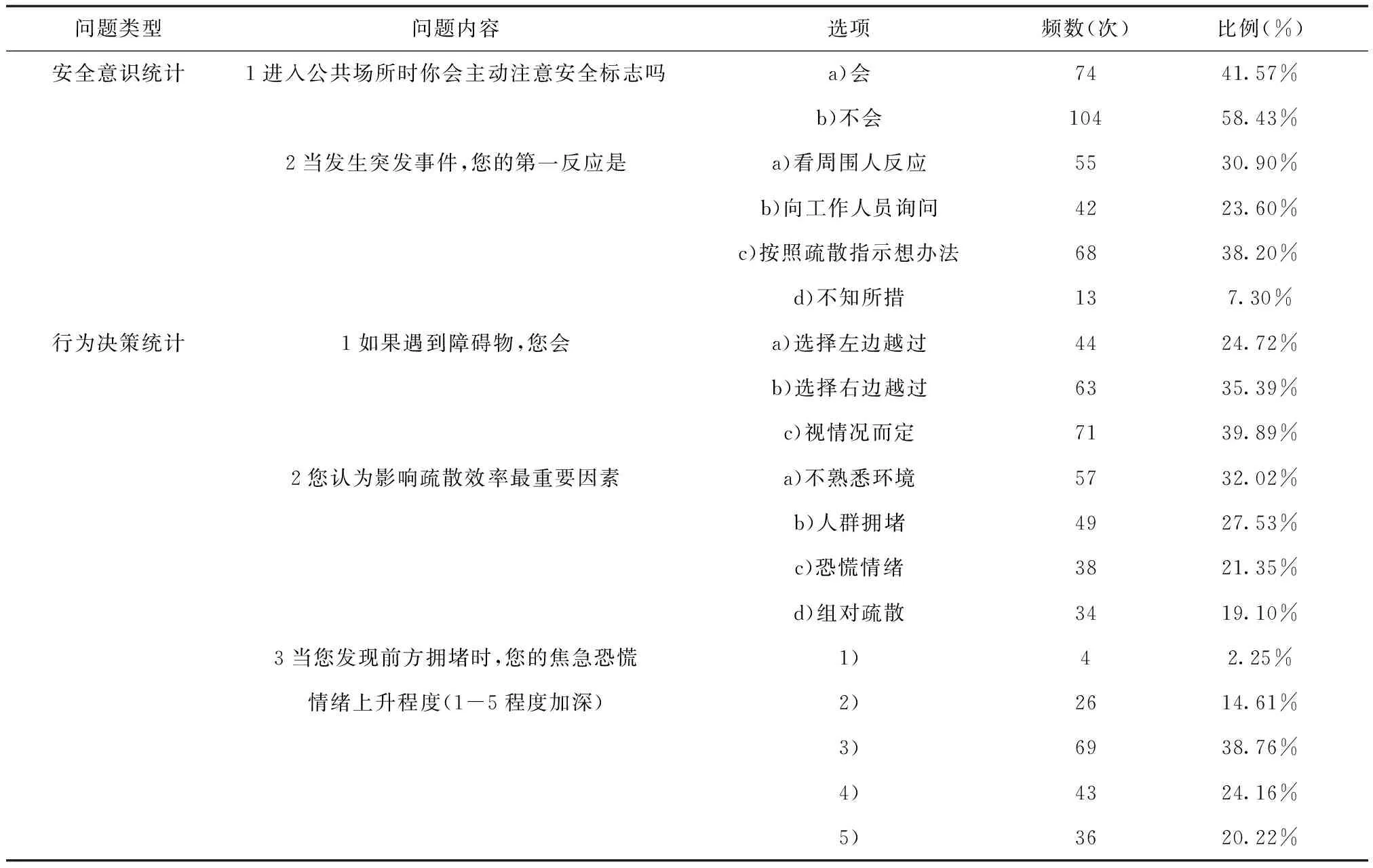
表1 老年人群疏散调查频数表

2.3 数据分析

在安全意识调查中，当事故发生时，只有38.20%的人会按照疏散指示开始疏散，54.4%会有一个判断过程和确认过程，但是仍然有7.3%的老年人当突发事件发生时不知采取什么措施，而这类人群需要的安全疏散时间(SET)会更大，这也从侧面反映出老年人群体面对突发情况时决定仍然滞后。

在行为决策统计中，老年人生理上的特殊性对听觉和视觉的影响较大，从而获取疏散过程周边信息的能力也较差。在遇到障碍物时，大多数人的转移要视现场情况而定，而对比之下，选择从右边的疏散人群比例高于左边，这和右边行走习惯有关，这也说明了紧张情况下，人们更加具有下意识行为的表现。80%以上老年人疏散会因为周边人群过度密集而加剧恐慌程度，原因是老年人疏散过程中不像年轻人那样机动性强、容易变道，一旦疏散过程出现拥堵，此类人更容易失去方向，从而提升恐慌程度，同时此类人群发现周边环境较为紧张时，如疏散过程减慢甚至停滞时，恐慌心理更加严重，所以在老年人疏散研究中，研究恐慌心理的老年人对比正常群体的疏散，显得更加重要。

综上所述，老年人的疏散除了具有一般群体疏散具有的跟从性特征外，此类人群还具有以下典型特征：

1)滞后性

指老年人在突发险情时，由于身体上的原因，导致接受信息和处理信息的迟钝，从而会对突发的安全问题，无法采取及时的行为举措，加大自身的受险可能性。

2)拥堵恐慌性

指老年人在疏散过程中，由于自身身体条件约束，在发生拥堵时，老年人不像年轻人可以采取有效迅速的换道措施，导致恐慌情绪的蔓延，容易停滞不前。这种情况在人群越密集处，老年人群行为决策受其影响越深。

3 模型

3.1 地场元胞自动机

地场元胞自动机模型将疏散空间划分为均匀的二维离散网格，每个网格为一个基本单元，每个基本单元尺寸为0.4×0.4m[6]，每个单元有占据和空置两种状态。通过引进静态场Sij和动态场D对模型进行描述，每个元胞处的人员以一定的转移概率选择移动至邻域元胞或不发生移动，本文邻域选取冯诺依曼型领域，如图1所示。

图1 冯诺依曼型领域

相比较传统微观行人流仿真模型，地场元胞自动机(Floor-field CA)具有很强的扩展性，通过对模型的改进，可以考虑许多不同的疏散行为特性，同时还可降低计算机计算难度，因此得到了国内外学者广泛应用，其中心元胞的转移概率计算如下：

pij=Nexp(ksSij)exp(kDDij)εij(1-ηij)

(1)

其中：ηij=0(元胞为空)；ηij=1(元胞被占据)；εij=0 时反映障碍物或者墙壁

N=[∑exp(ksSij)exp(kDDij)εij(1-ηij)]-1

其中Sij为静态场强度，反映当下元胞的静态场值，其值与当下元胞到出口的距离成反比，不随时间变化，距离越远值越小，距离越近值越大，定义边界和障碍物的静态场强为0，ks代表静态场的权重系数，值越大代表疏散人群对周边环境越熟悉，Sij计算如下。

Sij=N[max(sij)-sij]

(2)

其中：sij=min{(i-iom)2+(j-jom)2}1/2

公式中N为无量纲化因子，sij为行人元胞到出口的最短距离，(iom，jom)为出口处第m个元胞的坐标。Dij为动态场强度，受到扩散参数α和衰减参数β的影响，反映了上一个时间步被占据元胞对行人的吸引程度。如果元胞ij在t-1时刻被人占据过，则其值加1，kD代表动态场所占的比例系数，其值越大，代表行人跟随上一个行人的期望强度。

Sij、Dij均为正值。(1)式中N为归一化参数，确保所有移动方向的概率之和为1。

3.2 改进的地场元胞自动机模型

根据前期问卷调查显示，80%以上老年人疏散会因为周边人群过度密集而加剧恐慌程度， Sharma认为恐慌程度会导致位移量减少，也就是越恐慌速度越低，同时这种现象又会蔓延这种恐慌心理，接着会传染到群体，从而影响整体的疏散效率。本文模型建立原理就是在上节传统地场元胞自动机模型基础上，通过引入恐慌场Fij来刻画周边密集程度对老年人疏散带来的影响，并对式(1)进行改进后提出了考虑老年人群疏散改进的地场元胞自动机模型：

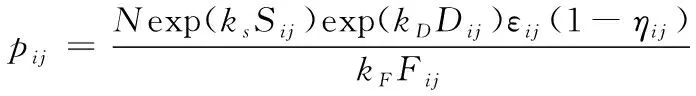
(3)

其中：

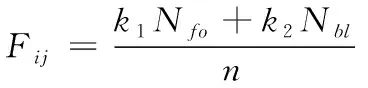
(4)

其中kF为恐慌系数，代表密集程度对老年人群的心理的影响，其值越大代表影响越深。恐慌场Fij按照式(4)计算，其中Nfo为前区被占元胞数，Nbl为后区所占元胞数。k1、k2为影响因子，由于行人疏散时前进方向上的人群对疏散心理影响最直接，这里设置k1>k2。n为视线空间内前后区空元胞个数，考虑到行人疏散时接收到的感官范围，这里设n为固定值25。N为归一化参数，其余参数定义不变。

图2 疏散前后区示意图

3.3 演化规则

模型采取并行更新原理，模型演化步骤如下：

步骤1：系统在框架内按照密度参数D均匀生成行人，同时按照密度参数d生成老年人，每个行人均有对应编号。

步骤2：按照式(2)计算每一个元胞的静态场值，该值不随时间变化。

步骤3：老年人群按照式(3)，其余群体按照式(1)计算转移概率后按照最大转移概率进行移动，更新位置。

步骤4：计算动态场值，初始值为0，在更新程序开始后，每个时间步内动态场值均发生变化，受扩散参数α和衰减参数β的影响，如果元胞ij在t-1 时刻被占据过，则其值加1。如果出现多个行人选择同一目地元胞，则随机选取一个行人移动到目标元胞上。

步骤5：重复步骤3和步骤4，直至所有疏散人员离开系统，仿真结束。

3.4 数值模拟及结果分析

本文研究了系统规模W=50前提下，行人每个时间步仅移动一个元胞，单个出口宽度L=7，T表示行人的疏散时间，单位是时间步(Time-step)，设置行人疏散速度为1m/s，则每个步长为0.25s。D为整体行人密度，定义为生成总行人数与元胞个数50×50的比值，d为老年人在整体行人中所占比例，本文参数采用已有研究[12]，其它参数经过敏感性校正后确定，设置kS=2000，kD=2000，k1=1.8，k2=0.4，kF=70。图3为模型疏散框架。

图3 模型仿真框架50×50

图4为模型参数设置群体行人密度D为0.2及老年人密度d为0.3时，经过Matlab对模型的仿真，分别对应(a)T=40个时间步、(b)130个时间步、(c)200个时间步时人群疏散时空示意图。疏散过程出现了疏散过程中典型的“成拱”现象，也间接验证了模型的有效性。

本文首先从整体密度D较低时开始仿真，当D设置为定值0.1时，逐步提升老年人群密度d，分析其对群体疏散效率的影响，单位时间内框架剩余人数越少则疏散效率越快，框架剩余人数随疏散时间T变化曲线如图5所示。

当设置D为定值0.2时，同理这里将老年人群密度d逐渐提升，在考虑老年人恐慌特性的前提下，分析其密度的变化下对人群疏散效率的影响，框架剩余人数随疏散时间T变化曲线如图6所示。

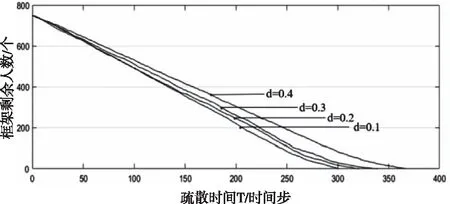
图6 群体密度D=0.2时，剩余人数随时间关系图

从图5和图6可以看出，当总人群处于较低密度时，老年人的比例增加对整体疏散的影响并不大，因此本文通过进一步增加人群整体密度来分析老年人不同比例下对疏散的影响，但在仿真过程中，老年人群是系统随机分散在仿真框架内的，因此随着行人整体比例增加，如果老年群体被随机分散在离出口较近或老年人群分散间距较小时，拥堵现象更早形成，导致恐慌情绪的影响加深，从而大大降低整体疏散效率；当被随机分散在离出口相对较远或彼此间距离较大时，仿真初期行人疏散较快，拱形形成和持续时间较短，因此同一行人密度D、老年人密度d下，疏散时间差距较大，为了解决这个问题，本文对同一密度D，d下分别进行10次仿真运算结果得到平均疏散时间，D取值范围为0.1-0.5，d取值范围为0-0.6，仿真结果如图7所示。

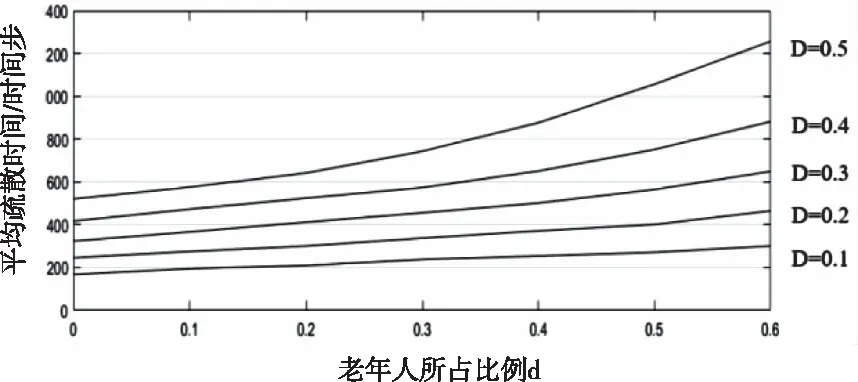
图7 平均疏散时间图

由图7可以发现，随着行人整体密度D增加，人群整体结构越来越紧密，恐慌心理对疏散带来的影响也越来越大，当人群疏散总密度低于0.2时，老年人所占比例对总体疏散产生的影响不明显，当整体密度D增加时，老年人所占比例对群体疏散的影响越来越大，当整体密度为0.4时，老年人仅占总密度的0.3，即对整体疏散产生较大的影响，因此在研究老年人的疏散时，恐慌心理对群体疏散的影响不容忽视。

4 结论

根据仿真结果可以得到以下结论：

1)本文以MATLAB作为平台，在单出口条件下时，提出的新模型可以描述出人群疏散出现典型情景，如人群出现拱形现象，拥堵现象等，这也证明了考虑恐慌特性的老年人疏散模型是有效的，仿真结果表明，当人群疏散总密度低于0.2时，老年人所占比例对总体疏散产生的影响不大；当人群密度达到0.4时，老年人所占比例仅0.3即对整体疏散带来较大影响，原因是因为人群过密时，增大了老年人的恐慌心理，即外在表现为停滞不前，在此情况下在整个疏散过程充当了随机障碍物的作用，特别是当人群开始在出口处拥堵时，老年人的恐慌心理极大影响人群疏散效率，同时也间接说明随着老龄化社会的持续加深，从安全角度讲，一些老年人出现频率较高的场所应当严格控制场所内的流量和人群密度。

2)本文仅对老年人的恐慌情绪做了研究，但就实际情况而言，个别老年人疏散时还存在着“激进”心理，表现为这部分老年人疏散时，往往高估自身身体条件，采取更加积极的变道，这种行为极易产生摔倒，从而对人群疏散产生更大影响，带来巨大的人员伤亡，因此这一心理在老年人疏散研究中不容互视，这将作为后期的研究方向加以研究。