关系化数据分块存储系统局部性时延优化算法

2021-11-17杨中杰王立中

计算机仿真 2021年4期

杨中杰，王立中

(内蒙古农业大学计算机技术与信息管理系，内蒙古包头 014109)

1 引言

存储系统作为计算机应用领域的重要组成部分，不仅与数据采集、预处理、处理、传输、转换等环节密切相关，而且系统的处理过程也比较复杂，因此在协同操作过程中可能会发生数据交叉操作。如何在保证系统稳定运行的同时，从根本上解决存储系统的实时性问题，同时增加数据量和用户，时延优化逐渐成为计算机领域的研究热点之一[1]。

赵晶等[2]提出了无线传感器网络多路径传输时延优化调度算法研究，基于传感器网络的多路径传输形式，探索复制机制与重传机制两种路由容错机制，并由此构建出两种多路径传输资源优化调度策略，实现数据成功传输的同时降低传输时延；林兵等[3]根据混合云环境的数据布局特征与科学工作流数据之间的依赖关系，制定一种混合云环境下面向时延优化的科学工作流数据布局策略，通过分析传输时延的影响因素，引入遗传算法的变异算子与交叉算子，设计出自适应离散粒子群算法，经压缩数据传输时延完成优化处理。吴建明等[4]分析以单点数据采集为主的光伏发电远程监测系统，基于物联网技术，对传感器的原始数据进行区分量化融合处理，实时准确地采集多通道数据，对数据采集输出信道加以均衡控制，提高了诊断数据的准确检测和分析能力。

对此，本文构建出一种关系化数据分块存储系统局部性时延优化算法，在理论创新方面，建立了关系数据块存储系统中关系数据的邻接关系，缩小了搜索范围，简化了计算过程和局部延迟优化分析过程。

2 存储系统关系化数据分块方法

2.1 关系化数据分块存储系统结构

关系数据块存储系统使用两个SCSI(Small Computer System Interface)通道来完成与下一层的两个分支的连接。统一存储空间主要由虚拟设备驱动程序组成。作为系统的中间节点，每个单元控制器都有三个通道，一个是上行通道，另两个是下行通道。SCSI从驱动程序和SCSI主驱动程序分别驱动上、下通道。系统的叶节点主要由磁盘结构组成。为了充分发挥关系数据组织的结构优势，最大限度地提高底层设备在数据传输中的并行性，并将其分块存储。如图1所示，磁盘的编号顺序是8个关系数据块的存储顺序。通过分块存储，可以有效降低主机数据请求的影响，充分利用块并行传输的容量。

图1 关系化数据分块存储系统结构示意图

2.2 关系化数据分块流程

2.2.1 关系化数据预处理

为了使数据满足存储要求，预处理可分为三个阶段：关系数据邻接关系的建立、数据法向量的预测和数据曲率的求解。在构造关系数据的邻接关系的过程中，通过寻找与当前关系数据距离最短的K个数据来构造K邻域。当关系数据量较大时，建立邻接关系可以有效地减少搜索面积，简化计算过程，降低计算量和复杂度，提高关系数据块的存储效率。关系化数据邻域求解的具体过程描述如下：

1)利用数据个数总和、最小包围盒体积以及邻近数据个数[5-6]，计算栅格边长，把最小包围盒分成规格完全一样的栅格；

2)根据非空栅格个数、栅格边长以及数据个数总和，求解关系化数据与数据中心之间的距离均值。

3)依据解得的栅格边长，再次划分最小包围盒为规格一致的栅格；

4)遍历所有数据之后，把数据与栅格进行一一对应地归类；

5)基于栅格的位置坐标，K邻域搜索[7]关系化数据的附近栅格，实现关系化数据邻域结构构建。

数据法矢预估阶段的目的是提升关系化数据分块的便捷度，利用最小二乘法，构架下列数据法矢预估表达式

(1)

基于预估的数据法矢结果，进行数据曲率求解阶段。假设数据曲面B=B(υ，ϖ)，则该曲面的第一基本形式与第二基本形式可分别用下列各式描述

Ⅰ=Ευ2+2Fυϖ+Γϖ2

(2)

Ⅱ=Λυ2+2Μυϖ+Νϖ2

(3)

由上式推导得出数据曲率的计算公式，如下所示

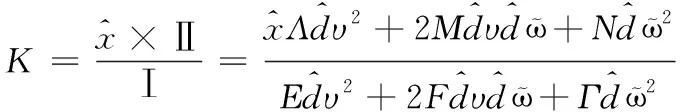
(4)

2.2.2 关系化数据分块存储流程

假设W为预处理过的关系化数据集合，曲面集合B={b1，b2，…，bn}的组成部分是关系化数据集合W，曲面集合B的子集是H={h1，h2，…，hn}，其中，n表示构成的曲面个数，当关系化数据集合符合下列各式所示的约束条件时，关系化数据的正确数据分块结果即为数据子集H

(5)

B(hi)=TRUE，ifandonlyΔ(γ(x′)，f(x′))≤ε

(6)

式中，第i个数据子集为hi，第j个数据子集为hj，当两子集为相邻子集时用Nbr(hi，hj)表示，尺度函数为Δ(γ(x′)，f(x′))，表示函数γ(x′)与f(x′)之间的差值，数据曲面hi与hj的重叠部分用B(hi∩hj)表示，标准差值是ε。

利用上述方法分块存储关系化数据，能够为存储系统的网络安全提供更有力的支撑。

3 存储系统局部性时延优化算法

假设关系化数据分块存储系统的网络结构用T表示，网络主节点是S，分块中的任意节点为t，则采用下列表达式界定从主节点到分块节点的局部性时延

(7)

式中，与分块节点t共享公共链路的损耗为Rkt，网络结构T中与节点t相邻的节点是k，该节点的荷载为Ak。

由于无法提前预知主节点S到分块节点t的实际路径，计算量过于繁琐，因此，导出局部性时延del(s，t)的上界Del(s，t)，简化关系化数据分块存储系统中的局部性时延优化分析过程，故得出下列表达式：

del(s，t)≤Del(s，t)=(Rd+r1L(s，t))(Am+c1W)

(8)

式中，Rd、Am分别表示存储系统损耗与荷载，r1和c1分别表示节点之间的传输链路损耗与荷载。

在一个二维曼哈顿平面上建立关系化数据分块存储网络结构，整个网络拓扑结构图G=〈V，E〉的顶点集合属于一个二维阵列，用V={v1，v2，…，vm}表示，相邻顶点间的边集合用E={e1，e2，…，em}表示。

如果存储结构T≤V为一个信号网引线端集合，通过在图G上求解时延优化的树结构，完成算法构建，该树连接结构T的全部顶点，且存在局部性时延del(s，t)的最小值。

时延优化算法的具体流程描述如下：

1)在图G上架构一个可以连接存储结构T中全部顶点的树框架，根据局部性时延del(s，t)的上界Del(s，t)，极大程度最小化del(s，t)；

2)将结构T含有的全部顶点设定成优化算法的初始节点，当前节点设定为正在分块的节点vj∈V，当算法开始运行时，当前节点变为vi∈T；

3)假设当前节点为vj∈V，该节点的坐标是(xj，yj)，则与节点vj对应的带权重心Cj界定过程具体如下：

设定当前节点集合R≤V，有vi∈R且i≠j

dij=(xj-xi)2+(yj-yi)2

(9)

(10)

(11)

(12)

式中，vj中带权重心Cj的水平与垂直坐标分别是xcj与ycj，权Dij的作用是令vj与vi节点带权重心更接近，明确当前节点方向[8]。

在构建树状结构的过程中，对每个步骤中的每个当前节点进行处理，使节点在一个方向上增长一个线段，得到一个边长e。一般来说，每个主节点S包括四个增长方向：上、下、左和右。如果节点沿着加权重心或主节点的生长方向生长，则可以减少局部延迟，因此，设置不同方向的不同权值。

4)假设当前节点vj的带权重心是Cj，节点邻接边是e，那么对应于带权重心Cj的权重表达式如下所示

wCj(e)=a1L(vj，Cj)

(13)

式中，L(vj，Cj)表示节点vj与带权重心Cj间的最短距离，a1表示邻接边与带权重心的方向关系，条件式如下所示

(14)

5)当主节点S是存储结构中的关系化源点时，节点vj的邻接边是e，则对应于主节点S的权值表达式如下所示

ws(e)=a2L(vj，s)

(15)

式中，L(vj，s)表示节点vj与主节点S间的最短距离，a2表示邻接边e与主节点S的方向关系，条件式如下所示

(16)

带权重心与主节点的权值界定形式如图2所示，在图中用点O表示。

图2 带权重心与主节点的权值界定示意图

根据式(11)，将上述两个方向同时作为时延最小化指标，采用合成方向界定相应权值wcd，使时延最小化

wcd(∈)=g1wCj(e)+g2ws(e)

(17)

式中，g1与g2为权重系数[9-10]，满足下列等式

g1+g2=1

(18)

通过调节权重系数g1与g2，能够改变带权重心与主节点权值在合成方向权值中的贡献，令时延优化更加合理、有效。

4 时延优化算法模拟分析

4.1 实验环境

为提升实验数据的可靠性与真实度，以Kaggle( https：//www.kaggle.com/datasets )中某远程监测系的实际应用数据为数据来源。表1为算法实现与实验相关软硬件配置。

表1 开发平台配置统计表

分别采用文献[2]、[3]、[4]方法以及本文算法展开仿真，通过各算法的节点生命周期、系统生命周期、通信距离以及局部性时延等实验数据，验证本文算法的有效性与可行性。

4.2 算法仿真评估

图3为各算法的节点生命周期实验结果曲线。

图3 节点生命周期误差曲线图

根据图3中，三种算法节点生命周期样本方差与存储系统所含节点个数的关系变化曲线图中，文献[4]方法在四种算法中拥有最大的节点生命周期样本方差，这说明该方法令系统中所有节点之间的能耗都呈不均衡状态；而本文算法通过寻找到与当前关系化数据距离最短的K个数据，架构了数据间的邻接关系，缩小了节点搜索区域，故节点生命周期样本方差最小，具有较好的能量均衡性能。

图4为各算法的系统生命周期实验结果曲线。