航空器地面畅通滑出时间研究

周 建，赵嶷飞，刘 宏，周 启

(1. 中国民航大学空中交通管理学院，天津 300300；2.民航江西空管分局管制运行部，江西 南昌 330114)

1 引言

在国家推进生态文明建设，促进节能减排和发展绿色民航的背景下，开展机场地面拥堵疏导不仅能提高航空器的地面滑行效率，同时可以减少航空器在地面滑行的燃油和碳排放。对航空器在机场地面畅通滑出时间进行精确预测，是开展机场地面拥堵疏导方法研究的重要前提。

FAA对畅通滑出时间的定义[1]为：航空器在理想运行(不受机场地面拥堵和天气等延误因素的干扰)条件下，从离开停机位到起飞离地过程的时间。

国内外对计算航空器地面畅通滑出时间已有研究，使用统计和回归分析方法占多数。2010年，Balakrishna P等[2]在预测航空器滑出时间时提出了深度学习算法，并用坦帕机场的运行数据检验效果较好。2010年，Jordan等[3]在以滑行距离和滑行速度为自变量基础上，使用序列浮动前向选择(sequential floating forward selection，SFFS)方法构建了航空器滑出时间回归模型。2013年，Ioannis等[4]在研究航空器离场过程建模和控制策略过程中，选取了起飞航空器调整数量作为地面滑出时间数学模型的自变量，未考虑落地滑入航空器数的影响；2014年，Ravizza S等[5]在预测航空器滑出和滑入时间时，构建了基于航空器滑行速度、滑行距离等自变量的多元线性回归模型；以上学者均认为落地滑入航空器数量与航空器滑出时间关联性不强。

2009年，Kistler等[6]选取了滑行距离、航空器停止数量、滑入和滑出航空器数量等参数为自变量，分别建立了线性和对数线性模型；2010年，Clewlow等[7]指出航空器滑出时间不仅与起飞排队航空器数量有关，还与落地滑入航空器数量具有较强的相关性，并建立了线性回归模型；2010年，John等[8]在建立航空器滑出时间多元回归模型时选取了起飞排队航空器数和落地滑入航空器数为自变量，但该模型的拟合优度R2仅为0.37；2016年，赵嶷飞等[9]国内学者对航空器滑出时间回归模型的自变量进行重新定义，将回归模型的拟合优度R2提高到了0.88；2017年，瞿也丰等[10]构建航空器地面滑出时间模型时，将自变量地面航班数定义为在时间窗口内，已从廊桥推出尚未起飞的航班数与已降落尚未进机位的航班数之和。

目前国内外学者在建立航空器地面畅通滑出时间预测模型时，在机型分类、样本数据区间选择、自变量选取、定义或计算方法等方面存在问题，导致回归模型的拟合优度偏低，预测偏差偏大。

本文首先选取航空器滑出数量和滑入数量为自变量，使用回归分析的方法，建立航空器滑出时间的数学模型，然后合理选取数据区间，对选取区间的数据进行非线性回归分析，最后建立了畅通滑出时间的对数正态分布模型，并计算出航空器的畅通滑出时间。

2 研究对象和变量选取

2.1 研究对象

本文以北京首都国际机场为研究对象。首都国际机场拥有T1、T2和T3共3座航站楼，以及36L/18R、36R/18L和01/ 19共3条跑道。

由于首都机场三跑道运行方向主要为由南向北运行，而且停靠在T3航站楼的离港航空器主要使用36R和01跑道起飞。因此本文的研究对象为停靠在531至536号停机位(编号为1)，以及停靠在451至458，408至413停机位(编号为2)，并使用36R跑道起飞的航班，如图1所示。

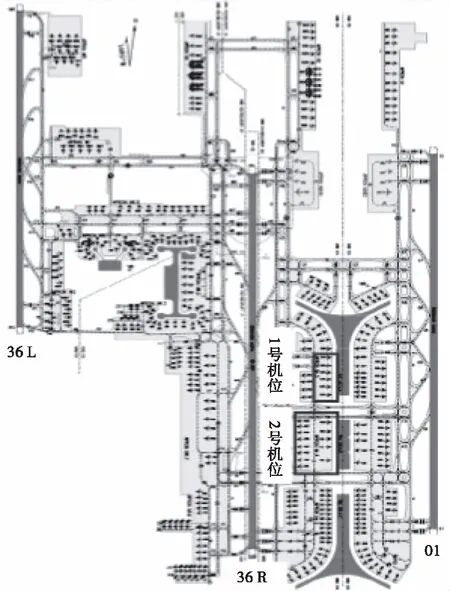
图1 北京首都国际机场平面图

2.2 变量选取

本文将从跑道资源占用的角度，在建立多元线性回归方程时，选取使用36R跑道起飞和落地的航空器数量为自变量，定义如下：

起飞航空器数量Di：在某架离场航空器i从廊桥推出至起飞离地过程中，使用36R跑道起飞的航空器数量；

落地航空器数量Ai：在某架离场航空器i从廊桥推出至起飞离地过程中，使用36R跑道落地的航空器数量。

离场航空器i的地面滑出时间计算公式为

(1)

2.3 数据处理

1)样本数据

对统计的原始数据进行多元线性回归，得出航空器地面滑出时间的初始数学模型

T滑出=1.65*D+2.18*A+2.69

(2)

2)数据筛选

在建立多元线性回归方程的过程中，发现某些时段样本数据的标准残差较大，影响因素包括航路限制、更换跑道和降雪等。因此，采用3σ原则剔除了约1%的异常点。

3)建立模型

对筛选后的样本数据进行多元线性回归，得出以下方程：

T滑出=1.64*D+2.08*A+2.80

(3)

该模型的拟合优度R2从之前的0.92提升为0.93。

2.4 散点图

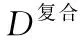
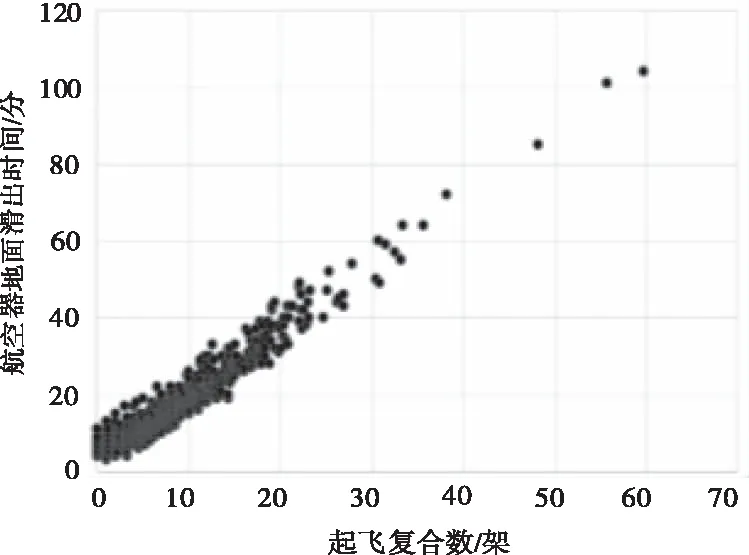
图2 航空器地面滑出时间散点图

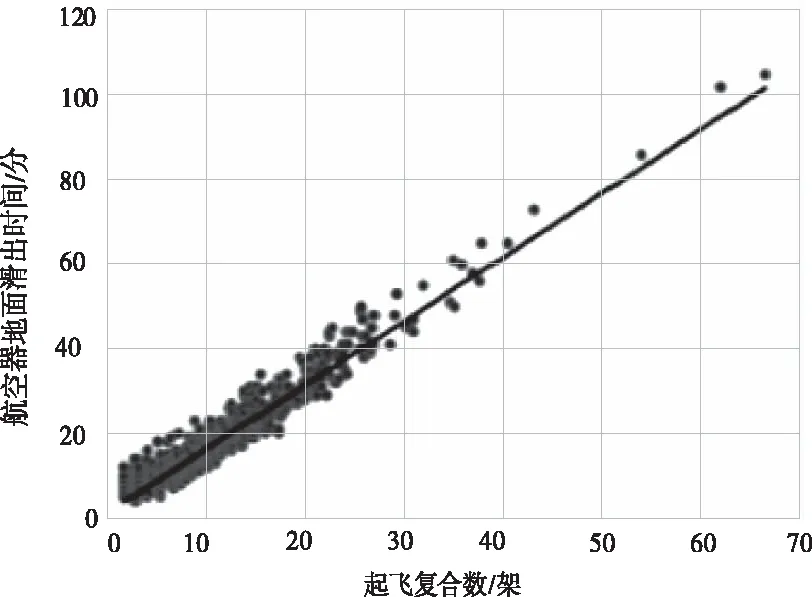
图3 航空器地面滑出时间拟合曲线图

D复合=D+A*2.08/1.64

(4)

T滑出=1.64*D复合+2.80

(5)

3 畅通滑出时间的计算

由于不同停机位、不同机型的畅通滑出时间均存在不同，因此本文对停靠在1号和2号机位区域的重型机和中型机的畅通滑出时间分别进行了计算。

3.1 1号机位重型机

1)数据区间选取

1号停机位区域内，重型机地面滑出时间的均值和中值如图4所示。

图4 重型机地面滑出时间均值和中值

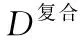
根据样本数据可得到前十个xj的取值如表1所示。

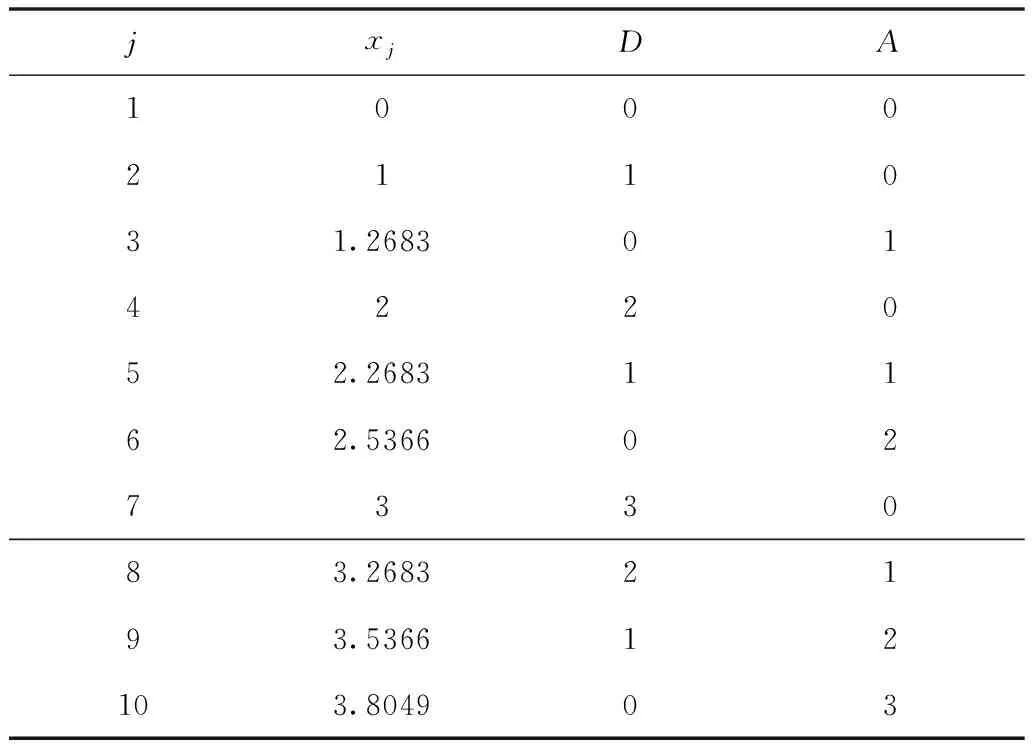
表1 X集合中的前十个xj

在表1中，x5=2.2683是指当起飞航空器数量D=1和落地航空器数量A=1时，根据式(4)可得起飞航空器复合数D复合=2.2683。

如表2所示，从U2开始进行回归拟合，得出不同Uj区间所对应的拟合斜率kj，kj有显著变化处即为临界点。

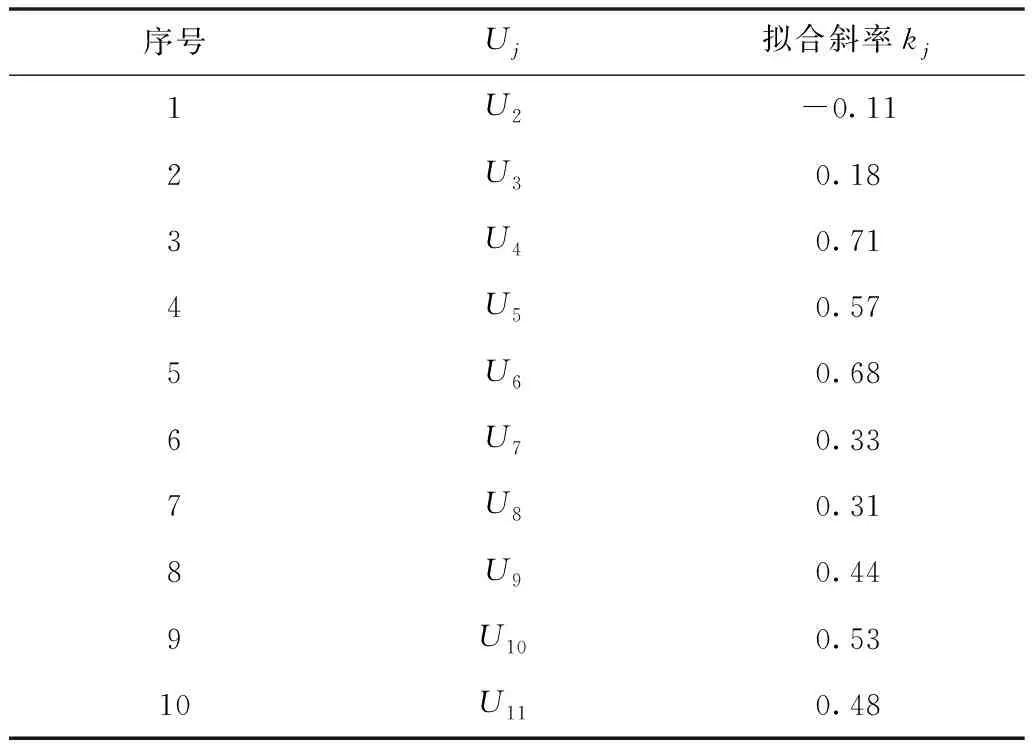
表2 不同起飞航空器复合数区间对应的拟合斜率

由表2可知，当x3=1.2683时，U3={x∈X|0≤x≤1.2683}，拟合斜率k3=0.18，当x4=2时U4={x∈X|0≤x≤2}，k4=0.71，数值是前者的3.94倍，之后的k值没有显著变化。因此，临界点取D临界=1.2683，其物理意义为：当起飞航空器数量D=0，落地航空器数量A=1，离场航空器的地面滑出时间等效于畅通滑出时间。

2)数据拟合

根据U3内重型机畅通滑出时间的频率分布，记y为畅通滑出时间的频次，建立对数正态分布模型如下

y=y0+c/(sqrt(2*PI)*σ*x)

*exp(-(lnx-μ)2/(2*σ2))

(6)

y=1.3673+44.9169/(sqrt(2*PI)*0.2383*x)

*exp(-(lnx-1.9456)2/(2*0.23832))

(7)

对应的拟合曲线如图5所示。

图5 重型机畅通滑出时间频率分布

3)畅通滑出时间计算

根据式(7)中的μ和σ值，计算对数正态分布模型的期望值为

E重型机=exp(μ+σ2/2)=7.20min

(8)

3.2 1 号机位中型机

1)数据区间选取

1号停机位区内，中型机滑出时间的均值和中值如图6所示。

图6 中型机地面滑出时间均值和中值

使用相同方法，临界点取D临界=2，其物理意义为：当起飞航空器数量D=2，落地航空器数量A=0时，离场航空器的地面滑出时间等效于畅通滑出时间。

2)数据拟合

y=0.741+29.4515/(sqrt(2*PI)*0.1919*x)

*exp(-(lnx-1.7772)2/(2*0.19192))

(9)

对应的拟合曲线如图7所示。

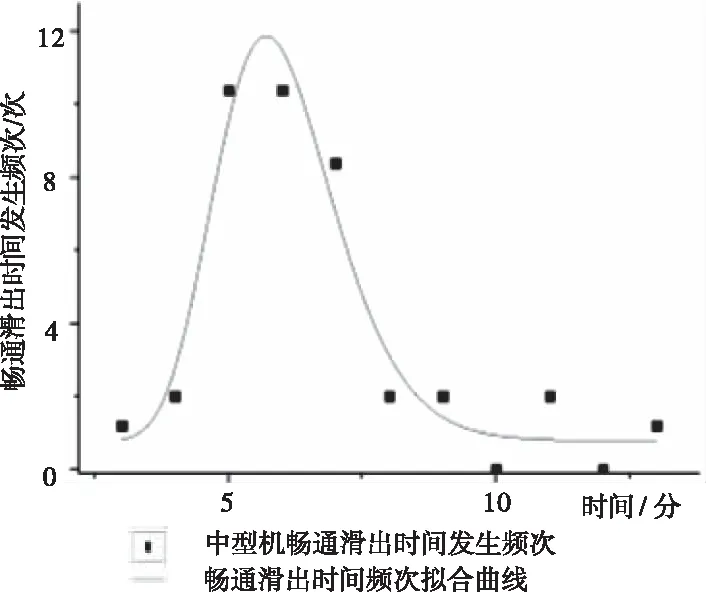
图7 中型机畅通滑出时间频率分布

3)畅通滑出时间计算

根据式(9)中的μ和σ值，计算对数正态分布模型的期望值为：

E中型机=exp(μ+σ2/2)=6.02min

(10)

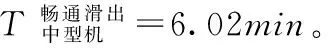
3.3 2号机位区域

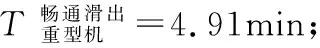
因此，对于停靠2号机位区域的航空器，重型机比中型机的畅通滑出时间多7.2%。

4 模型的验证

为检验航空器畅通滑出时间数学模型的预测准确度，选取停靠在1号停机位区域，且在不同时间段运行的航班数据进行验证。

4.1 重型机

2019年7至10月，停靠在1号停机位区域并从36R跑道起飞重型机的实际畅通滑出时间和预测畅通滑出时间对比如图8所示。

图8 重型机畅通滑出时间的实际值与预测值

重型机畅通滑出时间的预测误差平均值为16.73%，误差范围在±3分钟内的预测准确率为94.12%。

4.2 中型机

2019年7至10月，停靠在1号停机位区域并从36R跑道起飞中型机的实际畅通滑出时间和预测畅通滑出时间对比如图9所示。

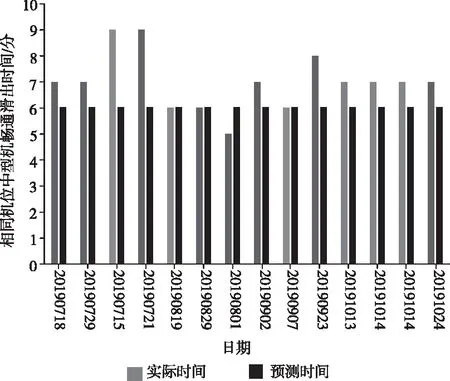
图9 中型机畅通滑出时间的实际值与预测值

中型机畅通滑出时间的预测误差平均值为15.01%，误差范围在±3分钟内的预测准确率为100%。

5 结束语

针对目前航空器地面畅通滑出时间数学模型在机型分类、样本数据区间选择、自变量选取、定义以及计算方法等方面的不合理问题，提出了改进的畅通滑出时间计算方法，并用首都国际机场实际运行数据进行检验，验证结果表明：

1)自变量选取合理。在构建地面滑出时间数学模型时，本文从跑道资源占用的角度出发，选取了在某航空器i从推出至起飞过程中，从36R跑道起飞和落地的航空器数量为自变量，模型的拟合优度R2达到0.93；

2)计算方法可行。本文首先使用拟合斜率法寻找样本数据区间的分割临界点，然后建立了畅通滑出时间的对数正态分布模型。经检验，1号机位区重型机畅通滑出时间误差范围在±3分钟内的预测准确率为94.12%；中型机畅通滑出时间误差范围在±3分钟内的预测准确率为100%；

3)考虑了停机位和机型的影响。本文综合考虑了停机位物理位置和机型的不同对畅通滑出时间的影响：①停靠的机位离起飞跑道越近，航空器的畅通滑出时间越短；②同等情况下，重型机比中型机的畅通滑出时间更长(1号机位区域多19.6%，2号机位多7.2%)，主要原因是重型机比中型机的开车时间更长；

4)误差产生原因。①原始数据中0.71%的航班缺乏起降时刻，对数据统计的完整性产生影响；②航班运行时刻数据没有精确到秒，对后期数据统计和分析的精确性产生影响；③原始数据中缺乏穿越36R跑道的航班信息；

5)后续研究。在建模过程中，没有考虑穿越跑道航空器数量和航路流量控制的影响，构建的数学模型仍有进一步优化的空间。