双轮驱动球形机器人的动力学建模与仿真

曾 鹏，许 逵，郑功倍，高丙团

(1. 贵州电网有限公司电力科学研究院，贵州 贵阳 550002；2. 东南大学电气工程学院，江苏 南京 210096)

1 引言

双轮驱动的球形机器人在一定程度上综合了轮式和履带式机器人特点，其结构相对简单，特别是本体具有“不倒翁”的不易倾覆特性，具有较强的环境适应性。球在滚动过程中阻力相对较小，且可以实现任意半径的转向运动，所以球形机器人具有运动效率高、能量损耗小的特点；此外，机器人的重要元器件和部件一般直接安装在球壳内部，密闭的球壳又为内部元器件提供了有效的保护，大大提升了球形机器人的安全可靠性，从而使得双轮驱动球形机器人在电缆管廊通道监测中具有广阔的应用前景[1]。

自1996年Aarne Halme等学者[2]研制出第一台具有真正意义上的球形运动机构以来，国内外的许多专家对于球形机器人展开深入研究[3]。根据已有研究，球形机器人主要通过质心偏移，在重力矩的驱动作用下实现运动驱动，根据其内部驱动机构主要可以分为四种形式：单摆驱动[4]、双摆驱动[5]、多质量体驱动[6]和小车驱动[7]。现阶段，对前三种结构的研究与应用较多，两轮小车驱动型机器人实现最为直观，且具有较好的爬坡越障能力；另外内部驱动小车可提供较大安装平台，可搭载安装各种传感设备；但是驱动车轮与壳体内壁之间必然存在的非完整约束也在一定程度上增加了双轮球形机器人动力学建模以及控制设计的难度；据了解国内还未有完善的两轮小车驱动球形机器人系统动力学建模的相关文献。

本文基于拉格朗日方程法[8]，针对双轮小车驱动的球形机器人建立了动力学模型，该模型完整描述了机器人在二维水平面内的多体动力学运动特性，有助于对球形机器人运动规律的理解以及后续的运动控制设计。最后，通过数字仿真验证了所建模型的正确性。

2 双轮驱动球形机器人动力学建模

2.1 球形机器人描述

双轮驱动球形机器人可由图1表示，包括结构图及其在OXZ平面投影的左视图和在OXY平面投影的俯视图；结合图1，建模涉及的变量参数定义为：球壳质量M，内部车体质量m；驱动轮质量mw，球体半径R，驱动轮半径Rw，车体质心距球心之间的长度l，静态下车轮接触球壳内的点到球心之间的竖直距离h，两个车轮之间轴距的一半d，小车质心与球心之间的连线与垂直方向的夹角θ，左右车轮滚过的角度θl和θr，内部小车前进方向与X轴正方向逆时针方向夹角φ，左右两侧电机的驱动转矩τl和τr，车体相对球心的等效转动惯量Jm，球壳相对球心的转动惯量JM，车轮关于车轴的转动惯量Jw，转向时球壳关于转向曲率圆心的转动惯量JφM，转向时小车关于转向曲率圆心的转动惯量Jφm，转向时小车车轮关于转向曲率圆心的转动惯量Jφw。

图1 两轮驱动球形机器人

2.2 基于拉格朗日方程的动力学建模

建模时做如下假设：

1)双轮驱动球形机器人的球壳厚度考虑忽略，且球体在地面上运动为纯滚动；

2)球内小车质量集中在其质心位置，即将其看作质点；

3)车轮转动时候与球壳之间无打滑。

设球体中心的坐标为(x,y, 0)，球内小车的质心坐标为(x0,y0,z0)，左车轮和右车轮与球壳的接触点分别为(xl,yl,zl)和(xr,yr,zr)。则左右车轮的位置坐标可计算如下

(1)

根据车轮线速度与角速度的关系，有

(2)

对于车体，有

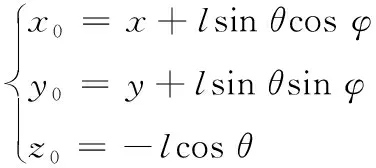
(3)

等式两边对时间t求导，有

(4)

在球形机器人转弯过程中，取一足够小的时间Δt进行分析，如图2所示。

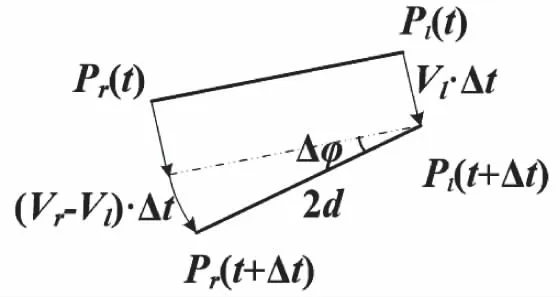
图2 转弯分析

以左边车轮作为参考，根据方向角φ逆时针为正的定义，转弯时右边车轮相对于左边车轮差速，转弯半径为轴距，即2d。在一段时间Δt内，右边车轮多走的距离为(Vr-Vl)Δt，方向变化Δφ，针对足够小的时间Δt，则可计算得到

(5)

当Δt→0时

(6)

基于以上的分析以及参数定义，根据拉格朗日方程建模方法，开始计算系统的动能和势能。内部小车的动能为

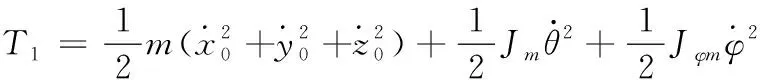
(7)

车体势能为

V1=-mglcosθ

(8)

车轮动能为

(9)

车轮势能为

V2=-2mwg(h-Rw)cosθ

(10)

球壳的动能为

(11)

V3=0

(12)

则可得到系统的拉格朗日函数为

L=T1+T2+T3-V1-V2-V3

(13)

采用拉格朗日方法建模时，可考虑的系统广义包括机器人位置坐标x和y，两个车轮的转角θl和θr，和球内车体的姿态角θ和运动方向角φ，但要注意其不相互独立。根据转弯分析，可通过车轮转角θl和θr计算得到方向角φ。假设球形机器人前进线速度为V，其对时间t积分即可得到球形机器人前进路程S。将前进线速度V沿XY轴分解，可得

(14)

即球形机器人的位置坐标x和y可根据前进路程和方向角求解得到，而方向角又与左右车轮的转角相关。所以，可确定考虑的系统有4个独立自由度。选取系统的广义坐标为

(15)

对应的广义力分别为

(16)

其中，Fl和Fr为车轮与球壳的摩擦力，本文定义其数值与车轮的转速成正比，即

(17)

实际中，需要考虑电机输出控制力矩时存在最大输出转速，从而导致球形机器人的滚动速度也是具有一定限制的。实际运动过程中，当球壳与驱动车轮接触点的速度比车轮转速高时，则摩擦力方向就会发生改变，从而使得球壳的速度不能进一步增大[9]。根据以上分析，可设定式(16)中的方向函数为

(18)

式(16)中Ff为球壳与机器人运动地面之间的摩擦力，根据机器人在地面做纯滚动的假设，摩擦力Ff可表示为

(19)

进一步，考虑到运动时球内小车驱动轮与球壳之间存在粘性，阻尼系数ξ，则在拉格朗日方程中引入耗散函数为

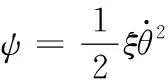
(20)

根据以上分析，进一步综合(4)(6)(7)(11)(14)可得由广义坐标表达的车体动能T1、驱动车轮动能T2和球壳的动能T3，进而将拉格朗日算子(13)、广义力(16)和耗散函数(20)代入拉格朗日方程

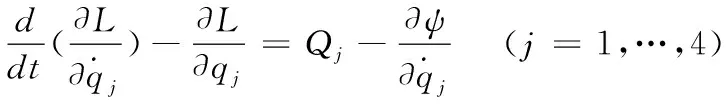
(21)

计算拉格朗日方程中的各项，整理得到球形机器人的动力学方程为

(22)

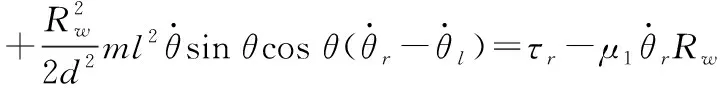
(23)

(24)

(25)

3 仿真研究

此时方向角的大小为

由此可得球形机器人运动轨迹的曲率半径为

(26)

在Matlab/Simulink环境搭建所建立球形机器人的动力学模型，机器人的基本物理参数为：球壳质量M=0.05kg，球内小车质量m=0.3kg，车轮质量mw=0.005kg，球体半径R=0.08m，车轮半径Rw=0.02m，车体到球心距离l=0.06m，车轮接触点到球心垂直距离h=0.048m，轴距的一半d=0.064m，重力加速度g=9.8m/s2。仿真中，通过直行运动和转弯运动这两组仿真来对球形机器人的动力学模型进行验证。

3.1 直行运动仿真

在直行运动的仿真中，设置左右车轮的力矩相等为0.04N·m，方向角初始值为π/4，其它状态量初值设置为0，得到图3所示仿真结果。从图3(a)可以看出，球形机器人沿着初始方向角π/4做直线运动，轨迹为直线，不转向运动，与前面理论分析一致。由图3(b)可以看出，在初始阶段，在恒转矩的作用下，为了保持动量守恒，小车向前运动，球形外壳即球形机器人向后运动，从而出现初始时刻机器人速度短暂为负的情况，完成启动后，大约经过2s机器人系统达到稳定平衡的运动状态，机器人整体沿着初始方向角做匀速直线运动。

图3 直行运动仿真分析结果

3.2 转向运动仿真

1)一般转向实验

在仿真模型中，所有状态量初值设置为0。给定两组不同的输入转矩组合：第1组，左轮不转右轮转τl1=0N·m，τr1=0.04N·m；第2组，左右轮转向相反大小不同τl2=0.03N·m，τr2=-0.02N·m。得到的仿真轨迹图如图4所示。

图4 转向仿真轨迹图

为了进一步观察转向时状态的动态变化过程，给出第2组输入转矩的系统状态量仿真曲线如图5所示。由变化曲线可以看出，在给定输入左右轮输入转矩下各个状态的变化趋势与图3所示直行运动仿真曲线变化情况类似，但是由于系统输入转矩的绝对值减少了，状态变化的幅值也一定程度降低了。

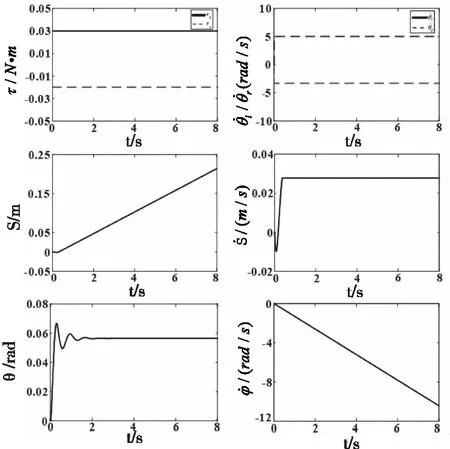
图5 τl=0.03N·m，τr=-0.02N·m时状态量图

2)原地转向实验

同样的各状态量的初值给定为0，设定左右两轮的输入转矩大小相等方向相反，即τl=-0.04N·m，τr=0.04N·m，得到如图6所示的原地转向仿真结果。

图6 零半径转向运动仿真结果

在图6(a)轨迹平面中只看到一个点，即原点，也是系统设置的初始位置，则说明在该类型输入力矩的作用下机器人不产生平面位置位移。由图6(b)状态量变化曲线可以看出，机器人的姿态角θ、运动路程S都没有变化，但方向角φ不断增加表明球形机器人在原地保持逆时针转动，这与前文的理论分析也是一致的。

4 结论

本文采用拉格朗日方程法，针对双轮小车驱动的球形机器人具体的建立了动力学模型。在建模过程中，由于方向角可由2个车轮滚过的角度确定，使用类似极坐标的思路描述了球体和球内小车的运动，选择4个直观的物理变量作为广义坐标进行建模，使得建模过程直观简洁。建模过程考虑了摩擦阻力的影响，所建立的模型更能反映球形机器人实际运动情况。基于建立的模型，在Matlab/Simulink环境下进行数字仿真，仿真结果与实际经验和理论分析相符，验证了模型的合理性与正确性。