基于蒙特卡洛方法的电磁辐射点信息检测仿真

董向国

(东北石油大学电子科学学院，黑龙江 大庆 163318)

1 引言

电磁辐射就是电子烟雾，通过空间传送的电能量和磁能量构成的。由电荷运动产生的电磁波，在大气中发射或者传递的现象就是电磁辐射现象[1]。由于电磁辐射检测专业仪器只能检测较简单环境下的问题，面对复杂的环境，仪器检测出的结果不精确，会存在大量的误差。如何对放射源进行检测成为该领域的重要研究方向，相关学者作出如下研究：

李奎等人提出了基于聚类分析的电磁辐射点信息监测方法。该方法主要以分析电磁辐射理论为基础，对电磁辐射点信息进行检测[2]。胡德洲等人提出了一种基于不同情况下电磁辐射点信息的检测方法。该方法根据电磁辐射理论，得出被测设备辐射干扰强度公式，根据电磁场仿真软件创建设备电磁辐射模型，由模型可以检测出设备的电磁辐射点信息[3]。张悦等人提出了基于混沌算法的电磁辐射点信息检测方法。该方法对待检测设备信息进行分析，然后根据混沌序列特征量对分析结果进行识别，最终得出电磁辐射点信息检测结果[4]。

上述检测方法主要针对近距离的探测，面对远距离的电磁辐射，在检测的过程中可能会存在强背景噪声的干扰和电磁辐射点信息源单一的现象，导致最终检测结果存在较大的误差。为此提出基于蒙特卡洛方法的电磁辐射点信息检测方法，蒙特卡洛方法能够将具有随机性质的事件清晰准确地描述出来，因此比较适用于针对电磁辐射点信息的检测工作。

2 蒙特卡洛方法实现电磁辐射电信息的检测

2.1 电磁辐射传递方程

蒙特卡洛方法实质上就是一个基于概率理论的方法，采用随机试验的方法对某时刻的概率和某随机变量的数学期望进行求解计算[5]。

假设某设备电磁波为N，每次辐射到的位置为Xi，i=1，2，…，N，想得到辐射伤害量，采用下式进行计算

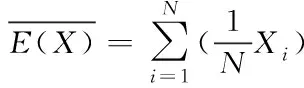
(1)

蒙特卡洛方法会依据概率1将期望值E(X)进行收敛，但是会存在误差，误差的计算公式为

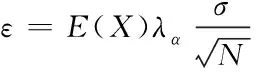
(2)

(3)

采用估计值作为计算值，表示随机试验的方差。若想要将误差尽可能降到最低，需要求解目标信息的后验状态分布p(Xk|Z1：k)的值，假设Sk表示为后验分布p(Xk|Z1：k)的随机采用集合，表达式为

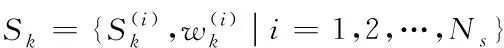
(4)

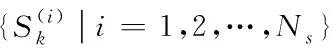
(5)

上述中假设的样本集合为p(Xk|Z1：k)，但是实际的应用中，p(Xk|Z1：k)一般不会直接得知，无法直接得到p(Xk|Z1：k)的解析解，这时需要找到一个适应的参考分布，该参考分布必须是一个已知的分布p(Xk|Z1：k)，并且容易对其进行采样，这样的分布称为提议分布或者称为重要性函数。

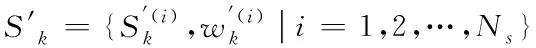
(6)

式中：wk表示没有经过归一化的权重，计算公式为

wk=E(X0，k)p(X0：k|Z1：k)

(7)

采用离散的形式将其近似的表示成

(8)

(9)

对权重的计算公式进行更新，得出

(10)

(11)

2.2 设备的电磁辐射点位置确定

蒙特卡洛法在对电磁辐射点信息进行检测时，电磁能量追踪过程中受到电磁辐射传递方程的约束，并不会得到电磁辐射强度的分布结果。

蒙特卡洛方法能将辐射传递过程中所有能产生影响的因素综合在一起，所以只需要考虑由计算时间和统计误差决定的准确值即可[9]。采用辐射传递方程描述能量在介质中传输时，能量的吸收过程、发射过程散射过程和投射过程之间存在一定的关系，即存在一个具有方向的能量平衡方程。电磁辐射在介质中的传递方程表示为

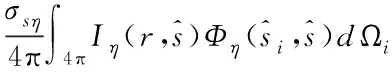
(12)

式中：η表示光谱参数，辐射在介质中传递要比在固体表面明显很多，因此物理性质和能量大部分采用光谱参数进行表示[10]。

将式(12)进行积分运算，得出的形式为

(13)

式中：s=|r-rw|，s′=|r-r′|表示将积分方向转换成向着s″方向。

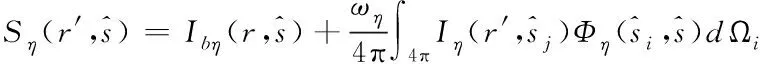
(14)

通常，在一个不透明的物体表面，边间条件可以表示为

(15)

式(14)和式(15)的结构十分相似，都是关于Ibη的项和Iη的积分项的和。在实际运用中，在物理领域中，散射和反射所代表的意义十分相似，其中散射是作用于介质中，而反射是作用于边界周围。

对式(13)、(14)和(15)进行物理分析，由于电磁辐射传输过程中电磁能量会减弱，部分区域r的辐射能量不仅取决于传输环境，还与距离较远的物体性质等因素有关，因此需要在辐射传递方程中引入指数衰减项。

根据对电磁辐射传递方程的分析，可以得出电磁辐射能束发射方向。电磁辐射向四周发射时，各个方向的发射机会都是均等的，将辐射发射点作为中心点，每个微小元体以球形方式向四周均匀发射。如图1所示。

图1 电磁辐射的笛卡尔坐标系

采用球形发射方式的坐标系为(r，θ，φ)，微元的体积计算公式为：

dV=(rsinθdφ)(rdθ)dr=r2sinθdθdφdr

(16)

因此体积单元V对ΔV的电磁辐射能量表示为

(17)

式中：κ表示电磁辐射特性参数。

通过对概率密度和联合概率密度进行设定，可以将式(17)重新整理表示为：

(18)

式中：QV表示体积单元V的总电磁辐射能量，P(r，κ)、P(θ)和P(φ)分别表示与衰减相关的概率密度函数、与方向角θ相关的概率密度函数和与方向角φ相关的概率密度函数。那么与方向角θ相关的方向概率分布表示为

(19)

同理可得

(20)

式中：Rθ和Rφ均表示0～1之间均匀随机分布的常数。

电磁辐射在整个环境中均匀发射，在直角坐标系下，坐标(x，y，z)附近体积微元dV发射电磁辐射的概率计算公式为

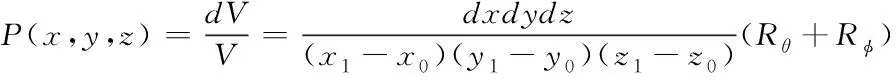
(21)

式中：x1，x0，y1，y0，z1，z0分别表示X，Y，Z三个坐标的极大和极小值。P(x，y，z)表示含有三个独立变量的联合概率密度函数，可对三个独立概率密度函数之积进行表示

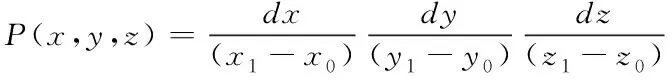
(22)

电磁辐射点坐标表示为

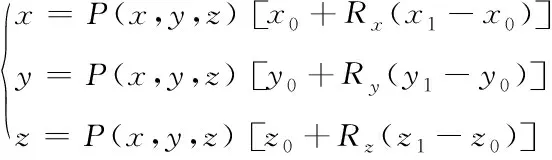
(23)

式中：Rx，Ry，Rz表示0～1之间均匀随机分布的常数。

获取电磁辐射点坐标后，即可完成对电磁辐射点信息的检测。因蒙特卡洛方法是基于随机试验原理，能够较为真实地对随机辐射的电磁波进行描述，且所受的几何条件限制影响较小，整体程序简单，计算量小，因此采用蒙特卡洛方法能够简便准确地实现对电磁辐射点信息的检测。

3 仿真证明

为验证电磁辐射点信息检测性能，设置实验环境为：CPU Intel Core i9-7980XE @ 2.60GHz，内存 8GB，运行内存 2GB，操作系统 Windows 10的计算机上搭建仿真环境，基于MATLAB数据库处理软件为实验平台创建仿真。

实验对象选为某市郊区的变电站，在变电站内依据通讯基站和主要设备等情况进行检测点的选取，并对其正常运行产生的电磁辐射进行研究。采用本文方法对该设备产生的电磁辐射进行处理，通过频谱分析仪得到电磁辐射点信息的频谱图，如图2所示。

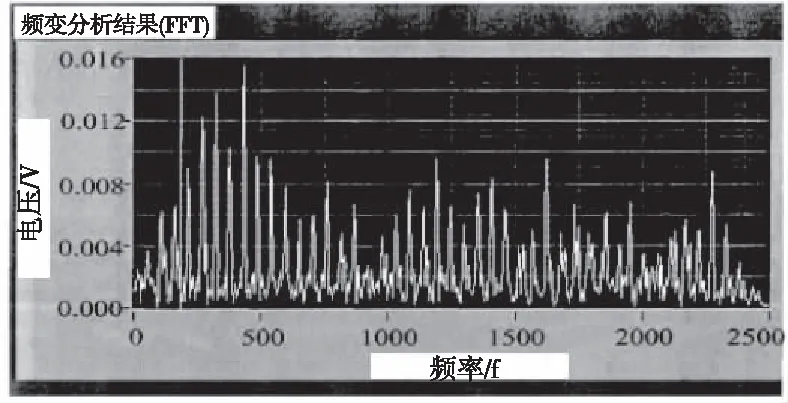
图2 电磁辐射点信息的频谱图

通过分析图2可知：对于变电站放电设备的电磁辐射来说，电磁辐射点离待检测设备越远，电磁辐射的能量越弱。本文方法能够较为精确地将电磁辐射点信息检测出来，说明本文方法具有较高的检测准确性。

电弧产生瞬间，电磁辐射信号出现幅值较大脉冲，起弧后电磁辐射脉冲随机出现，并且脉冲幅值有可能大于起弧瞬间出现的首个脉冲。在试验中，仅针对电弧产生瞬间的首个电磁辐射脉冲进行幅值分析，实验结果如图3所示：

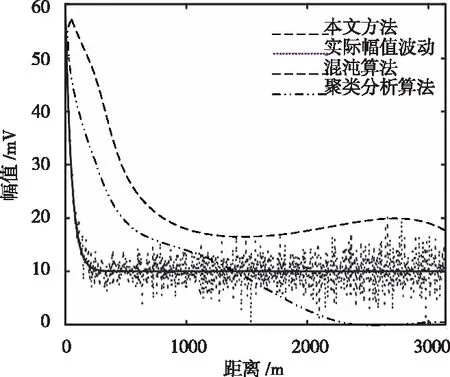
图3 不同方法电磁辐射的幅值

由图3可以看出，三种方法的整体幅值变化都随着距离的增加而呈现降低的趋势，基于混沌算法的电磁辐射点信息检测方法的幅值在距离为1000m之前与实际幅值相差较大，但是当距离超过1000m后，幅值的变化趋势较为平稳，本文方法的整体变换趋势与实际幅值的变化趋势相近，且相差较小，可以很好的实现对电磁辐射点信息的检测。

使用 HFSS 软件仿真天线在1GHz、3GHz、5GHz在H面的方向图。

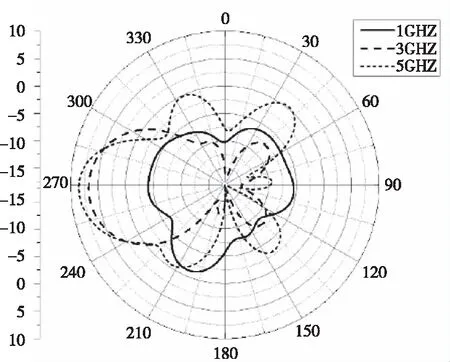
图4 天线实测 H 面方向图

从实测的天线方向图可以看出，在高频段天线的方向图也没有发生明显的开裂现象，说明该天线在实际使用中有较好的辐射特性。证明本文方法能够较为精确地将电磁辐射点信息检测出来，说明本文方法具有较高的检测准确性。

4 结束语

本文针对电设备存在的电磁辐射检测问题，提出一种基于蒙特卡洛方法的电磁辐射点信息检测方法。该检测方法运用蒙特卡洛思想，对电磁辐射传递方程进行求解。因蒙特卡洛方法对目标模型和噪声没有限制，并且不要求后验部分必须满足高斯分布，可以对任何形式的检测问题进行处理，采用随机采样原理，当样本数量比较多时蒙特卡洛方法能够得到收敛的检测结果。本文方法虽然能够对电磁辐射传递方程进行求解，但是基于蒙特卡洛方法的电磁辐射点检测方法仍需得到进一步研究，应用范围应该进一步扩大。