基于能量衰减矩阵的矿井目标定位方法
2021-11-17贺方圆王文清
贺方圆,刘 婷,王文清,吴 雪
(1.中国矿业大学(北京)机电与信息工程学院,北京 100083;2.北京银行,北京 100013;3.北京工业职业技术学院,北京 100042;4.中央民族大学经济学院,北京 100081)
1 引言
目前基于指纹数据库的矿井目标定位方法因其具有能够降低非视距误差、减少多径效应影响的效果而受到矿井目标定位的重视[1]。在基于指纹数据库定位时,为了规范定位点,经常将定位区域网格划分,对矿井目标的定位其实是对目标所在网格的定位[2]。
常用的表示目标位置的方法有距离表示法、信号能量表示法等[3-7]。实际生产应用中,在建立指纹数据库时对每个网格进行距离或信号能量测量的做法非常繁琐且不易实现,即使做到也是将每个网格划分的面积较大而网格的总数很少,这种情况严重影响了矿井目标的定位精度。文献[2]提出了一种交叉标注的指纹数据库建立方法,该方法区别于传统的多人标注方法,仅需1名工作人员便可以完成数据库的信号采集工作,但该方法仍需工作人员遍历所有网格进行数据采集,采集工作量很大。文献[3]提出一种改进的Kriging插值算法,该算法通过插值能够降低50%的数据需求,但众所周知,矿井巷道可长达数百米乃至上千米,因此即使降低了一半的工作量,剩余的一半数据采集工作也是相当繁杂的。
本文结合压缩感知模型提出一种基于能量衰减矩阵的矿井目标定位方法。该方法主要分为三步,第一步将定位区域进行网格划分并建立网格位置坐标和网格序号一一对应的指纹数据库,第二步首先构建测量矩阵和基于能量衰减模型的稀疏矩阵,然后利用改进的贪婪匹配跟踪算法重建目标位置信号,第三步将位置信号和数据库进行比对以确定目标的位置坐标。该方法将煤矿井下定位区域中的目标定位问题转化为利用构建的测量矩阵和能量衰减稀疏矩阵重建目标位置信号的问题,在实现精准定位的同时极大程度减少了构建指纹数据库的工作量。
2 系统模型
矿井目标定位系统包含井下设备和井上设备两部分。井下设备包含信号接收模块(定位分站)、信号发送模块(定位目标)、信号整合传输模块、井下服务器、交换机,主要任务是完成定位分站接收各个定位目标发射过来电磁信号并上传到地面目标定位模块;井上设备包含监控模块,目标定位模块,井上服务器,交换机等,主要任务是将井下传来的目标信号进行处理重构出目标位置信号并和数据库进行比对,确定目标位置。井下和井上可以通过工业以太网进行通信。其硬件组成如图1。
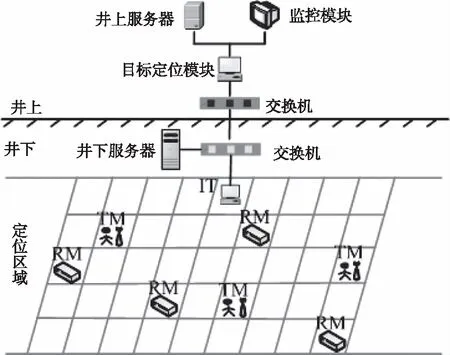
图1 定位系统硬件组成示意图
图中RM表示定位分站,其随意布置在巷道定位区域内,用以接收定位目标发来的电磁信号;TM表示定位目标,定位目标随身佩戴信号发射器,定时向周围发射电磁信号;IT表示数据整合传输模块,用以整合各个定位分站发来的测量数据并上传到井下服务器;井下服务器用以保存和上传数据至井上目标定位模块。目标定位模块将井下上传的数据处理并确定目标的最终位置;监控模块实时在线监视反馈目标位置是否偏移,并对监控管理人员作出相应警示;井上服务器用以存储定位数据。
3 指纹数据库
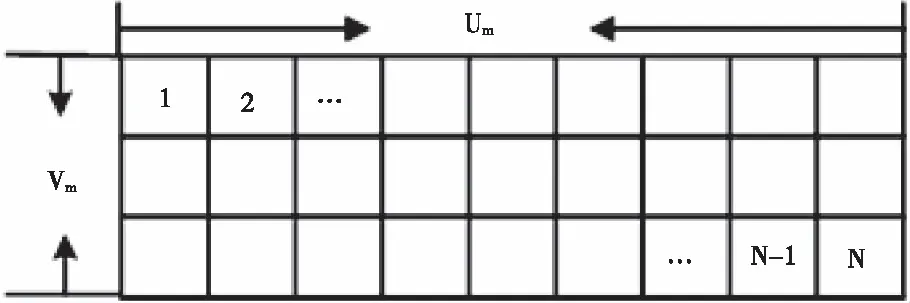
图2 定位区域网格划分
指纹数据库是在目标定位前就构建好并存储在井上数据处理模块中。在构建数据库时,定位巷道首先被划分为N个网格,将网格按照一定顺序从1到N排序,然后对每个网格进行位置坐标测量,确定每个网格的位置坐标与对应序号,网格坐标为平面二维坐标。在对网格位置坐标测量时,当已知其中一个网格位置坐标和序号时,便可根据定位巷道的长宽和定位精度推算出每个网格位置坐标和序号,无需再将每个网格坐标都测量一遍,如图2。若定位巷道长为Um,宽为Vm,当定位精度取1m,即网格的长宽为1m时,巷道被划分为N个网格,测量的第一个网格坐标为(x1,y1),则全部网格序号和其对应位置坐标可表示为
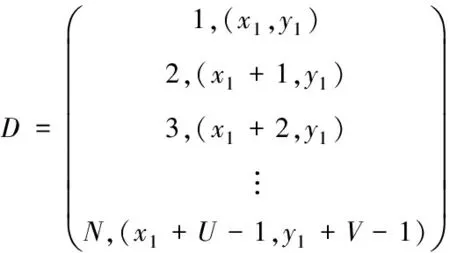
(1)
其中,N=UV,D即为构建的指纹数据库。同理,若已知任一其它网格位置坐标和序号时,推算方法类似。
在得到完整的指纹数据库时,在定位阶段就可将重构信号与离线指纹库进行比对,得到目标人员所在网格位置。
4 目标定位算法
4.1 目标信号重构方法
基于压缩感知模型[8],若X为长度N的一维稀疏向量,稀疏度为k(即含有k个非零值),则根据稀疏信号的少量采样值即可恢复信号X,恢复模型为
y=ФX
(2)
其中,y为长度为M的一维测量向量,即采样值,Φ为测量矩阵。此方法就是在已知测量向量y和测量矩阵Φ的基础上,求解欠定方程得到原向量X。一般的自然向量X本身并不稀疏,需要在某种稀疏基上进行稀疏表示:
X=Ψα
(3)
其中,Ψ为稀疏基矩阵,α为稀疏系数(α只有K个是非零值,K< y=ФX=ФΨα=Aα (4) 式(4)中将原来的测量矩阵Φ变换为A=ФΨ,A被称为传感矩阵,解出α的逼近值α′,则原向量X′=Ψα′。 要想从y中恢复X,就需要求解如式(5)所示的线性方程组优化问题 (5) 求解式(5)是一个组合优化问题,是一个NP难题[9]。实际上,当矢量X长度N和非零个数k均较大时是无法实现的。但是,如果当矩阵ФΨ满足约束等距性质或者不相干时[10],那么上述问题就可以松弛为l1范数最小凸优化问题 (6) 如果测量值y受到噪声扰动,那么式(4)将变为 y=Aα+ε (7) 其中ε为一未知误差扰动。 本文算法参考压缩感知模型,将目标位置看作稀疏信号α,构建测量矩阵Ф和基于能量衰减的稀疏矩阵Ψ,并利用重构算法恢复目标位置信号。 借鉴压缩感知模型,对比定位区域划分的网格数,巷道内定位目标的数量很少,因此可以将定位目标看做是一个N×1维的稀疏信号α α=(α1,α2,…,αN) (8) 将网格按1-N排序,排序方法需和指纹数据库网格排序一致。α中每个元素代表一个网格,元素下标对应网格序号,其中αr∈{0,1},r∈(0,1,…,N),即网格有目标时αr=1,无目标时αr=0。在求解出目标信号α后,将其与数据库比对,α中不为零的元素序号对应数据库中相同网格序号的坐标值即为目标的最终位置。因此在求目标位置时只需求出α中不为0的元素序号即可,即求解出α中不为零的第r行即代表第r个网格中有目标。 基于巷道电磁波能量衰减模型,可用y代表网格内任意布置的M个定位分站实际测量到的电磁信号强度,一个网格内最多布置一个定位分站,y为M×1维列向量。第一个定位分站测量到的信号强度就是y中的第一个元素,第二个定位分站测量到的信号强度就是y中的第二个元素,以此类推,M个定位分站测量到的信号强度组成了M×1的列向量。 测量矩阵Ф是一个M×N的矩阵,它的作用是对信号起到降维作用。Ф的每一行可以看作是一个定位分站,它与稀疏向量X相乘,选取了向量X的一部分信息。定位分站采集到的这一部分信息足以代表原向量X,并能找到一个算法来高概率恢复原向量。M个定位分站任意分布在N个网格中。因为每个定位分站测量的是位于不同网格位置传递过来的信号强度,所以矩阵Ф中每行只有一个元素为1,其余元素都为0,M< (9) 记Ф(e)为第e行的1×N维向量,除Ф(e,f)=1外其它元素都为0,其中f指定位分站所在的第f个网格的序号。 若N个网格都按序逐一布置有定位分站和目标发射器,稀疏能量衰减矩阵Ψ便为N个定位分站分别测量N个网格目标得到的信号强度组成的矩阵,第一个定位分站测量的第一个网格目标的信号强度为矩阵第一列的第一个元素,第二个定位分站测量的第一个网格目标的信号强度为矩阵第一列的第二个元素,以此类推,N个定位分站对第一个网格目标测量的信号强度组成Ψ矩阵的第一列,N个定位分站对第二个网格目标测量的信号强度组成Ψ矩阵的第二列,N个定位分站对第N个网格目标测量的信号强度组成Ψ矩阵的第N列,矩阵元素与测量的网格目标信号强度相对应的示意图如图3所示。 图3 矩阵元素与网格目标信号强度对应示意图 若采用上述的测量方法构建能量衰减矩阵,过程会非常繁琐和复杂,在实际工程中很难实现。本文利用信号衰减模型构建矩阵Ψ,在定位区域N个网格中,每个网格(定位分站)可测得一组信号强度值,定位分站位置p测量目标位置q的信号能量可以采用目标能量衰减模型[11,12]粗略表示,表达式为 (10) 其中,Epq表示分站位置p测量目标位置q的信号能量强度,E0为位置p处的信号强度,Dpq为位置p与位置q的欧几里得距离,D0为目标物理尺寸,是一个常数,β∈[2.0,5.0]为根据环境变化的衰减指数。因此基于信号衰减模型,定义N×N的目标能量衰减稀疏矩阵Ψ为 (11) 在式(4)中,已知测量值y、测量矩阵Φ和稀疏基矩阵Ψ,要想求得代表目标所在位置的向量α,本文引入一种基于贪婪算法[13]改进的匹配跟踪算法来重构向量α,重构后解出的α中不为零的第h行即代表第h个网格中有目标,由此得出目标位置。 贪婪匹配追踪算法[14]在每次迭代过程中能识别多个元素,这使得它能够快速的收敛,同时避免了阈值选择的难题。该算法主要包括以下几个重要步骤:从现有采样值生成等价中间过渡信号,并定位中间过渡信号中最大分量的位置,从而估计出目标信号。 相应的伪码如下: 输入:感知矩阵A=ФΨ,信号测量矩阵y,稀疏度K。 输出:重建目标信号α′。 当没有满足结束条件时,循环执行步骤1)~6)。 1)K←K+1。 3)更新索引集ΛK=ΛK-1∪Ω,并相应更新已找到的感知矩阵中的列集合AK=[AK-1AΩ]。 6)更新残余分量:r=y-Aα′。 为了分析本文提出方法的性能,本文选择长、宽、高分别约为20×4×3.5 m3的一段矿井巷道模拟受限空间环境,如图4。选择将类矩形巷道的20×4 m2的平面区域划分为N=80个网格,并且将M=5个型号为2×2 11b/g/n Wireless LAN M.2 Adapter的信号接收模块(定位分站)随机部署在类矩形巷道网格内,其中M< 图4 定位仿真场景图 图5 目标和定位分站布置图 在MATLAB仿真中,通过改变N、M和SNR来测试网格大小、定位分站数量和噪声带来的影响。由于在仿真中需要考虑本文恢复算法相对于其它恢复算法在定位方面的优越性,因此也对三种不同恢复算法中相应参数进行分析比较。同时为了防止随机性和偶然事件对定位结果的影响,本文在运用MATLAB进行仿真时,所有的仿真结果都是在100次重复运行的结果上取平均值,实验中忽略测量误差。 图6所示为当N=80不变时,定位分站数量M由1变化至13每增加2个定位分站测量一次,运行本文算法求得的实际距离误差值。从图中可以看出随着M的增大距离误差逐渐减小,当M=11时,本文算法可以100%的估计出所有目标的位置。由此得出本文算法是一个高准确率的有效稀疏重构方法。 图6 N=80时,改变M时的定位误差 图7所示为当M=5不变时,网格数量N由30变化至80每增加10个网格测量一次,运行本文算法求得的实际距离误差值。从图中可以看出随着N的增大距离误差逐渐减小。 图7 M=5时,改变N时的定位误差 最后在相同的实验环境下,即3个目标点,5个定位分站,80个网格,将本文算法与Cluster[15]、FTTD[11]和Binary[16]三种传统目标定位方法作对比,定位结果见表1。 表1 定位误差及算法平均时间统计表 表1表明,本文算法在各点的定位效果具有明显优势。本文提出的定位算法平均计算时间明显少于其它算法,即时间复杂度有明显下降,并且其在定位精度方面具有明显优势,很好地平衡了定位精度和定位效率之间的矛盾。 针对井下人员目标定位系统低功耗和实时性的要求,本文结合压缩感知模型提出了基于能量衰减矩阵的井下人员定位的方法,其主要优势和特点如下: 1)建立指纹数据库时,通过定位区域网格划分,以及在获取定位区域大小,定位精度,任一网格序号和对应位置坐标后,经计算获得所有网格的序号和对应位置坐标,形成指纹数据库,该方法大大降低了建立数据库的工作量。 2)目标人员定位时,基于压缩感知模型,构建观测矩阵和稀疏矩阵,将人员定位问题转化为稀疏信号恢复问题,即可得到目标人员的位置信息。在构建稀疏矩阵时,利用能量衰减模型,可以推导出稀疏矩阵中每个元素的值,无需再对每个定位点一一测量。 3)运用改进后的贪婪匹配跟踪算法来重构信号,本文模拟了在实际情况中运用本文所提方法重构信号,并通过变换不同参数和其它三种算法做比较,结果表明本文所提算法定位精度最高,平均误差达到0.6445m,满足定位精度的要求。同时,本算法的时间复杂度较低,平均耗时也低于其它三种算法。

4.2 目标稀疏信号
4.3 测量向量和测量矩阵

4.4 稀疏能量衰减矩阵
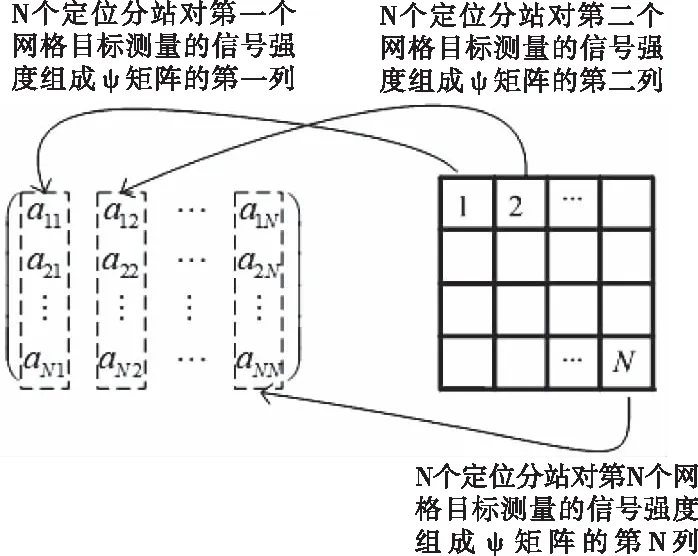
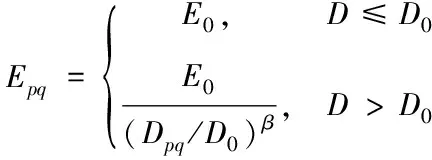

4.5 改进贪婪迭代重构算法

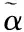
5 仿真结果





6 结论
