基于梯度方向的Canny SLIC图像分割算法
2021-11-17郭昕刚屈诺希
郭昕刚,王 佳,屈诺希,程 超
(长春工业大学计算机科学与工程学院,吉林长春130000)
1 引言
图像分割是一种将图像分成各具特性互不重叠的技术过程,它是人工智能和计算机视觉中最基础的预处理手段,图像分割的好坏会直接决定图像融合和图像识别的精度[1]。在文献[2]中,Ren等人首次提出了超像素的概念,其目的是为了将具有相似颜色和轮廓等低级语义信息的像素归为一类,以便于将点集问题转成区域集问题[3],来降低计算量,改善后续工作的处理效率。现阶段,很多人将超像素方法和边缘检测算法结合在一起,构成具有较好边界粘附性的超像素分割图[4]。文献[11]中所提出的Canny SLIC算法就是利用Canny算子检测出来的边缘信息,来进行SLIC超像素分割的,从中可以看出Canny算子检测出来的边缘信息能够决定超像素与图像边界之间的粘附性。而边缘检测,也是图像处理中最重要的过程之一。许多传统的边缘检测算法在科研中也会被经常使用,像Sobel、Prewitt、Canny等。其中最常使用的是Canny边缘检测算法[5],此算法与其它传统的边缘检测算法相比,其性能各方面都是最好的,并且许多领域的研究专家都在Canny算子的基础上提出了各种改进的边缘检测算法。如Er-sen li对图像梯度幅值的计算和OTSU边缘自动阈值选取的方法做出了改进,在一定程度上取得了良好的成果[6]。而对于传统的Canny SLIC算法,使用的传统的Canny边缘检测算子抗噪能力较差,易将弱边缘信息识别成噪声,从而导致Canny SLIC算法产生的分割图中部分边缘的粘附性变差。
为此,本文提出了一种基于梯度方向的Canny SLIC图像分割算法。它是把利用边缘和噪声在梯度方向上的差异而改进的Canny算子和SLIC算法相结合,来保护图像的弱边缘信息并提取出完整的轮廓,最后再使用六边形来描绘超像素,从而生成令人满意的超像素分割图。
2 相关算法介绍
2.1 传统的Canny算法
1986年,Canny提出了Canny边缘检测算法和最佳边缘检测的三个评估指标:低出错率、最优定位和最小响应[7]。传统的Canny边缘检测算法分为四步:
第一步是图像去噪。由于Canny算法对噪声十分敏感,所以为了防止噪声引起错误检测,要先使用二维高斯函数来消除噪声。

(1)
在(1)式中:σ为高斯滤波器的参量,它是用来控制滤波器模糊图像的程度。σ越小,滤波器定位性越好、信噪比越低。反之,滤波器定位性越差,信噪比越高。因此,要结合实际情况,合理选择σ。
第二步是计算梯度特性。在图像中,边缘可以指向各个方向,因此传统的Canny边缘检测算法采用边缘差分算子来计算2×2邻域内各像素点的水平和垂直方向的梯度,从而获取梯度的幅值图像G和方向图像θ。其中,点(m,n)处的水平偏导数Gx(m,n)和垂直偏导数Gy(m,n)采用Solbel算子来计算,公式如下
Gx(m,n)

(2)
Gy(m,n)
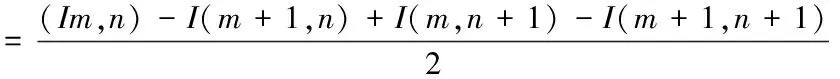
(3)
故此时点(m,n)处梯度的幅值和方向可由下式得出

(4)

(5)
其中θ∈{0°,45°,90°,135°},分别代表水平、垂直和两个对角线等四个方向。由于边缘灰度值变化明显,所以通过计算图像中所有像素点的梯度特性,可以得出可能的边缘点。
第三步是非最大约束。它是一种只保留局部最大值的细化边缘的方法。通常通过第二步得出来的梯度边缘不止有一个像素宽,而是有多个像素宽,所以为了精确定位目标边缘并保证每条边的宽度为1像素,便采用非最大约束(NMS)来细化边缘。在梯度幅值G中,为了计算更加准确,Canny算法会沿着种子点周围八个梯度方向进行线性插值。
如果G(m,n)的强度大于梯度方向上的两个插值结果,那就将点(m,n)标记为边缘候选点。反之,就标记为非边缘点。最终,通过NMS就能得到一个候选边缘图p。
第四步是滞后阈值。Canny边缘检测算法中最关键的环节是用滞后阈值检测和连接边缘,而使用滞后阈值要先选取高低两个临界值。在Canny算法进行完第三步非最大约束后,会产生候选边缘图p。在图p中,如果像素点的梯度幅值超过高临界值,则将此点标记为边缘点;而如果像素点的梯度幅值低于低临界值,则将此点标记为非边缘点;而对于梯度幅值处于高低临界值之间的像素点,就标记为边缘候选点。最后,再根据边缘之间的连通性,判断此像素点的相邻像素点中是否有边缘点,若有,就把此点记为边缘点。反之,记为非边缘点。
2.2 SLIC和Canny SLIC
2.2.1 SLIC
在2010年,Achanta和Shaji提出了SLIC超像素算法[8][9]。它复杂度低,实现简单,速度快,被广泛应用于图像分割中。其实质是一种局部的Kmeans聚类方法[10]。但它与kmeans聚类算法有所不同:SLIC算法只在每个聚类中心周围2S×2S的区域内搜索相似的像素点,而kmeans算法是在全局内搜索相似的像素点。图1、2展示了上述两算法在搜索区域上的差别。

图1 SLIC算法 图2 kmeans算法
其次,SLIC算法将像素分组到一个五维的特征空间中,并将其分解成一个五维特征向量[l,a,b,x,y]。其中[l,a,b]是CIELAB颜色空间的分量,[x,y]是像素点的空间坐标。而在SLIC中,两个像素之间的相似度是由它们之间的向量距离D来衡量的(D与相似度成反比)。其计算公式如下
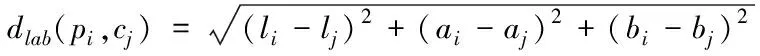
(6)

(7)

(8)

2.2.2 传统的Canny SLIC
传统的Canny SLIC算法能够将内容敏感的轮廓信息给标注出来[11],产生保持较好边界的超像素。首先它通过Canny算法检测出图像中的边缘信息,然后在欧式距离中增加一个函数G(pi,cj)用来判断某一像素是否为边缘像素。若cj到pi的路径中存在任何边缘像素,则G(pi,cj)就等于边缘像素对应的梯度值gl之和;反之,G(pi,cj)等于[]。相应数学公式定义如下:
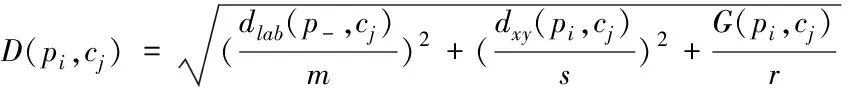
(9)
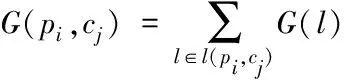
(10)
在(9)式中r是归一化常数,能决定Canny边缘检测在D(pi,cj)中的相对贡献量。其余变量皆为上文所述。在(10)式中,l(pi,cj)表示像素pi到cj的路径中所有像素构成的集合。G(l)则表示:如果l是边缘像素,G(l)等于l点的梯度值;反之,G(l)等于0。
与传统SLIC算法的步骤相比,Canny SLIC要先使用Canny边缘检测做初始化处理,计算出所有像素点的梯度值,然后随机选取j个聚类中心,并以固定长度S来初始化每个聚类的中心cj。其次,为了不让中心点选在较大边缘或噪声点处,选取中心点8邻域范围内梯度值最小的点来作为新的中心点。紧接着设置两个数组d(pi)和l(pi)分别用来存放像素点到聚类中心的最小距离和最小距离对应的中心类别标签,并分别将其初始化为0和∞。最后在每个中心点cj周围2S×2S区域内为每个像素点pi分类,如果D(pi,cj)小于d(pi),就把D(pi,cj)赋值给d(pi),并将此聚类中心的标签j存放到l(pi)中,重复迭代此过程,直至所有像素点pi被正确分类。
3 基于梯度方向的Canny SLIC
传统的Canny SLIC算法是在传统的Canny边缘检测算子的基础上实现的,但传统的Canny边缘检测算法存在很多缺陷。比如滞后双阈值的选取,若通过人工来选取,很容易将双阈值定高或定低,从而导致部分幅值低的弱边缘被忽略。所以本文采用一种基于梯度方向的Canny边缘检测算法来改进Canny SLIC算法[12],从而使其对弱边缘的分割精度更加完善。
3.1 基于梯度方向的Canny算法
在Canny边缘检测算法中,描述一个像素点的特性除了梯度的幅值之外,还有一个重要的信息量——梯度的方向。边缘像素的梯度方向,通常是指向边缘的法线方向,而干扰噪声是没有固定的方向。所以基于梯度方向的Canny算法能够更好地识别弱边缘区域,进而让Canny SLIC算法能够更好地分割出弱边缘区域。

图3 两种算法的比较(矩形框出了两种算法的部分区别)
3.1.1 算法原理
基于梯度方向的Canny算法它是在中心点的8邻域范围内,来进行边缘检测的(如图4)。首先,在此算法中定义两个参量Sm和Am。Sm是每个中心点0与其8邻域内各个像素点的连线,其数学表示为:Sm={(0,m)/m=1,….,8}。结合图4,可以轻松理解:当中心点0与其邻域内某一点都处于同一类的边缘上时,其连接Sm也处于此类的边缘上。而Am表示中心点0与其邻域内某一点m的连线Sm的法线方向与此两点的梯度均值方向的夹角的绝对值,此参量能够辨识边缘点和噪声点的方向。当中心点0与其邻域内某一点都处在同一边缘上时,Am的幅度值就会小于一个较小的值T;反之,对于敏感的噪声点,其方向不固定,故Am的值就会很大。
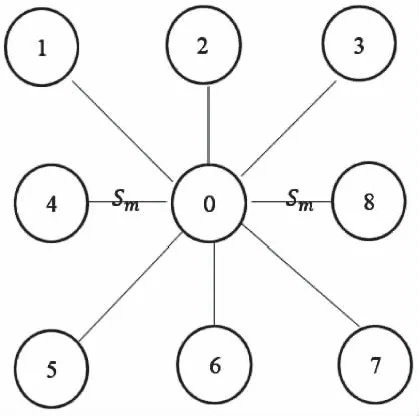
图4 基于梯度方向的Canny算法的原理图
基于梯度方向的Canny算法工作流程如下:
1) 先搜索通过非最大约束得到的边缘候选图p,然后判断p中任意一点p(m,n)的8邻域内有无其它边缘候选点,若无,转到第6步,否则:
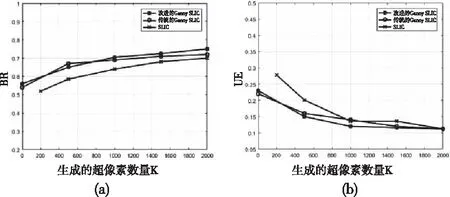
3) 继续在点p(m,n)的3×3邻域内,搜寻没有被记为边缘点的边缘候选点,并求其对应的Amt值。如果存在Amt 4) 将通过上述几步获取的邻域中心p(m,n)及满足Amt 5) 如果mt的3×3邻域范围内有边缘候选点,但是此点没有被记为边缘点,那就把该点记为边缘点,然后再以该点为新的中心继续连接,直到全部的中心点的3×3邻域范围内没有被标记的边缘候选点,执行第2步; 6) 继续搜寻图p,直到找到新的边缘候选点,如果该点没有被记为边缘点,执行第2步,否则再继续搜寻其它点,直到不再有新的未被标记为边缘点的边缘候选点出现为止,算法结束。 基于梯度方向的Canny边缘检测算法,可以充分的将图像中的弱边缘区域识别出来,并有效的区分出弱边缘点与噪声点。将此算法与SLIC算法结合,能够使SLIC具有更好的边界约束力,进而分割出更加完整地超像素分割图,且分割精度得到进一步提高。此外,本文将传统的Canny SLIC算法中的参数r定义成某一聚类所对应的所有像素点的梯度值之和,公式如下 (11) 其中n为聚类中心cj的类别j,G(pi,cj)为式(10)所述。 基于梯度方向的Canny SLIC算法实现步骤如下: 1) 先在原始图片上使用基于梯度方向的Canny 算法,计算出所有像素的梯度值和边缘点;然后使用复数运算将检测到的边缘点从二维降至一维,来提高判断某一像素点是否为边缘点的速度; 3) 初始化两个列表,分别用来存放像素点到聚类中心的最小距离和最小距离对应的中心类别标签: 对每个像素设置类别数组l(pi)=-1; 对每个像素设置距离数组d(pi)=∞; 重复 4) 分组步骤: for每一个聚类中心cjdo for每一个像素点pi在中心点cj周围2s×2s区域内do 计算cj和pi之间的距离; if D(pi,cj) d(pi)=D(pi,cj) l(pi)=j end end end 迭代 计算并修正聚类中心cj; 计算并修正新聚类中心位置与先前聚类中心位置之间的残差误差E; Until E<=设定阈值。 实验结果是在win7系统和matlab平台上实现的,实验所采用的数据集为公开数据集BSDS500,本节将从超像素分割图和评价指标来分析本文算法。 图5展示了本文算法在不同的超像素数量k和颜色权重m下的分割结果。图像结果表明,本文算法与其它超像素算法一样,m越大,超像素之间就越规整,m越小,超像素之间就越紧凑,对图像边界的依附性就越好。 图5 基于梯度方向的Canny SLIC算法分割结果 图5中,超像素数量k=[200,800,1000],颜色权重m=[8,10]。按列来:(a) k=200的分割结果;(b) k=800的分割结果;(c) k=1000的分割结果。 将基于梯度方向的Canny SLIC算法与传统的Canny SLIC算法和SLIC算法,在BSDS500数据集的500幅图像进行了分割比较。图6是本文算法与传统的Canny SLIC算法和SLIC算法的部分比较图,舍弃传统的正方形采用六边形来描绘图像,其可以使超像素更加贴合边缘。从图中可以看出传统的Canny SLIC算法由于传统的Canny边缘检测将弱边缘点识别成噪声,所以导致部分弱边缘欠分割;而改进的Canny SLIC算法能将图像中的弱边缘点与噪声点较准确地分割出来,使分割精度更加贴合真值(groundTruth)。 图6 三种算法的超像素分割结果图(K=600,m=10) 图6中,(a)为本文算法分割结果;(b)为本文算法分割图的部分放大图;(c)为传统的Canny SLIC算法分割结果;(d)为SLIC算法分割结果。 超像素分割图是从人的视觉上来反映分割结果的优劣程度,而超像素分割方法的性能指标是从有效性上来反应图像分割结果的优劣程度[15]。为了检验本文算法的分割有效性,采用常用的性能评价指标边缘召回率BR和欠分割错误率UE[16]。BR表示超像素分割边界在一个小邻域内检测到的真值边界的分数,其数学定义如下 (12) 其中,b(s)表示所用算法产生的超像素边缘分割结果,b(g)表示手工分割的边缘真值,函数I(·)是用来判断算法产生的超像素边界点是否在b(g)中的像素θ的区域内,A(·)表示每块超像素分割区域的面积。 而UE是用来衡量算法生成的超像素超出超像素真值范围的程度,其数学表示为 (13) 其中,A(·)表示每块超像素区域的面积,gm表示手工分割的边缘真值,Sn为生成的超像素块。本文算法的两种分割性能的评价标准如图6:通过图6可以看出基于梯度方向的Canny SLIC算法对测试库中的数据集分割效果是准确的。 图7 边界召回率BR(A)和欠分割错误率UE(B)的趋势图 图7中,BR越高,UE越小,分割结果越贴合边界。 本文提出的基于梯度方向的Canny SLIC算法,能够很好地解决弱边缘区域的边界依附性以及超像素形状规则问题。它通过基于梯度方向的Canny边缘检测算法,得到包含弱边缘信息的清晰边缘像素点,然后使用复数运算将检测到的边缘点从二维降至一维,来提高SLIC判断某一像素点是否为基于梯度方向的Canny算法检测出来的边缘点的速度,最后将边缘强度加入到欧式距离中,进行聚类。实验数据表明,本文算法与传统算法相比有效地提高了图像弱边缘信息的分割精度,为图像分割的进一步发展奠定了基础。3.2 基于梯度方向的Canny SLIC的算法实现
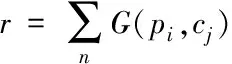

4 实验结果分析
4.1 实验结果图分析


4.2 评价指标


5 总结
