一种分布式的点球弹簧修匀法并行方案

昌继海，赵铭伟，余 飞，关振群*

(1.大连理工大学工程力学系，辽宁 大连 116024;2.大连理工大学电子信息与电气工程学部，辽宁 大连 116024)

1 引言

在求解边界运动等非定常流动问题时，针对网格变形问题的并行化研究是求解几何变形问题的重要方向[1]。网格变形方法主要分为插值类方法和弹簧类方法[2]两大类。

插值类的网格变形方法将流体内部网格节点的位移视为边界节点的插值问题，该类方法由于在变形过程中不考虑节点之间的连接性，直接通过边界节点的位移对内部节点进行插值，不需要迭代，容易实现并行化，许多研究者都对插值类方法的并行化进行了研究。Boer[3]等人提出的径向基函数法(Radial Basis Function， RBF)是一种易于并行的插值方法，该方法通过选取特定的径向基函数，利用边界节点对内部节点进行插值得到内部节点的位移；Rendall[4]和曾[5]等人在RBF方法的基础上进行了改进，如通过贪婪算法减少插值点的数目等等。Li[6]和Fang[7]等人提出了基于主从架构的并行方法来提高RBF法的并行效率。此外，刘[8]等人提出的背景网格法也是一种易于并行的插值类方法，但是该方法面临凹边界的几何问题或者推广到三维问题时会遇到困难。

物理类方法主要包括Batina[9]等人提出的弹簧类方法，该方法将网格类比为一个由弹簧组成的弹性系统。相比于插值类变形方法，对弹簧类变形方法的并行化研究较少，一方面是由于弹簧类方法变形能力较弱；另一反面，弹簧类方法在计算过程中还要始终考虑节点之间的连接性，需要求解大规模的线性方程组，导致计算效率较低。

一些研究者提出了许多改进的弹簧类方法，如增加扭转弹簧[10]或垂直弹簧[11]等方式来提高变形能力。基于这些改进的弹簧类方法，Ma[12]和程[13]等人进行了分布式并行化的研究，取得了较好的并行效率。

林[14]等人在Ball-vertex弹簧法的基础上提出一种局部插值的点球弹簧修匀法(VerBSS)方法，该方法通过分解弹簧系统的方式对网格进行逐点求解，具有插值类方法的特征，是一种求解效率较高的网格变形方法。

本文在林等人的基础上，采用分区和共享单元层的策略，提出了一种分布式的VerBSS并行方案，既保留了该算法较高的变形能力，又实现了较高加速效率的并行化。最后，通过算例对本文提出的VerBSS并行算法和共享式并行方法的变形能力进行了对比，在二维和三维情形下对该算法的加速性能进行了测试。算例结果表明这种并行方案变形能力较强，具有较高的并行效率，适合推广到大变形、大规模的网格变形问题。

2 基于弹簧模型的方法

2.1 Ball-vertex弹簧法

普通弹簧法的原理，是将网格的边看作弹簧，其刚度与其边的长度成反比。相邻的节点i和节点j之间的力fij可表示为

(1)

ui和uj分别为节点i和节点j的位移，kij为ij弹簧的刚度，nij为节点i到节点j的单位向量。为避免这种现象的出现，通过在三角形节点与其对边之间插入垂直弹簧来阻止单元塌陷，如图1a)所示，p点为i节点到边Ejk的垂线的垂足。这种垂直弹簧称为Ball-vertex弹簧。

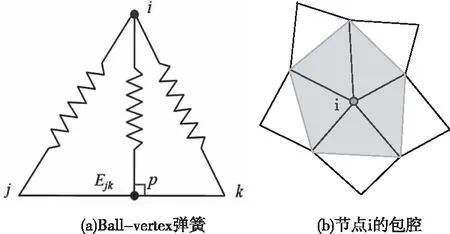
图1 Ball-vertex弹簧法

Ball-vertex弹簧作用在节点i上的弹簧力可表示为

(2)

其中up和ui分别为节点p和节点i的位移，kip为ip弹簧的刚度，nip为节点i到节点p的单位向量。p点的位移可以通过节点j和节点k的位移插值获得，为

up=ξuj+(1-ξ)uk

(3)

其中ξ为节点在边Ejk上的插值系数。因此，ip弹簧作用在p点上的力可分解为作用在j点和k点上的分力。则节点i上的弹簧系统线性方程组为

(4)

其中K为节点i的刚度矩阵，u为子弹簧系统各节点的位移向量，b为i点的载荷向量。

2.2 VerBSS算法的流程

VerBSS方法的求解方式不同于普通的弹簧方法，该方法通过在每个内部节点的闭包上形成一个以该节点为核心，以所有与该节点相邻接的节点为外围边界的多边形或多面体闭包，如图1b)所示。

VerBSS算法：

输入：初始网格M0

输出：变形网格M1

Step1：导入初始网格，查找所有内部节点，建立点及其周围节点的拓扑关系。

Step2：为每个内部节点构建多面体包腔的子弹簧系统，并对刚度矩阵K进行LDLT分解，将分解后的L矩阵和D矩阵，以及转换后的右端项存储起来。

Step3：将已知边界的节点位移u代入式(4)，遍历网格内部节点进行计算，并统计内部节点位移量变化，作为收敛条件。

Step4：判断Step3是否满足收敛条件，若不收敛，重复step3，直至收敛。

3 VerBSS的分布式并行方案

3.1 VerBSS并行算法的通信方式

本文采用METIS分区工具将初始网格划分为若干个分区[15]，进行任务划分。每个子分区相应的节点和单元的数据存储在各自的存储区域，通过拓宽相邻分区边界的方式来形成共享单元层，使得这些分区边界上的节点被纳入到求解序列中，如图2a)和图2b)所示为初始网格和分区后的网格。

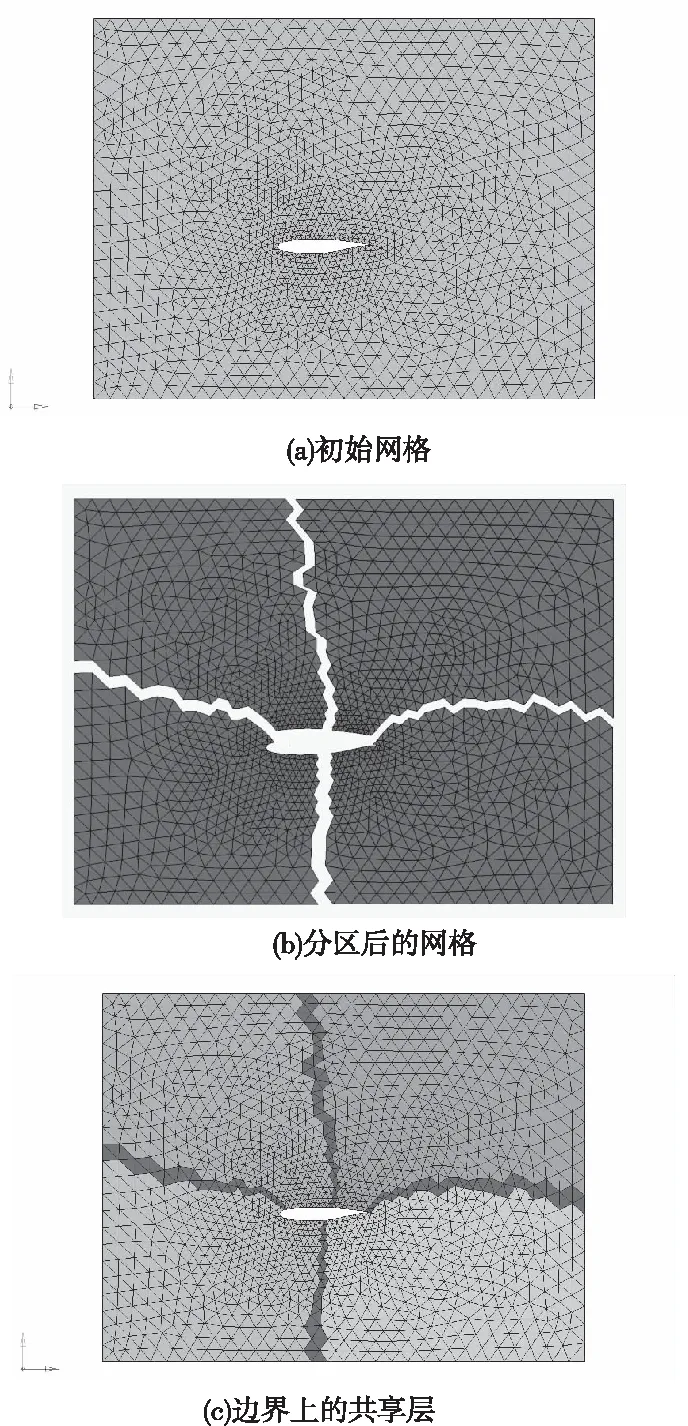
图2 二维机翼流场网格分区

选择一个分区将其边界上所有与边界线相连接的单元的几何信息传递给其邻接分区，那么这些共享单元线将拓宽为一层共享单元面，相邻的两个分区共享这层单元面，共享单元层如图2c)所示。三维情形中的共享单元面将拓宽为一层共享单元墙，相邻的两个分区共享这层单元墙。通过构建相邻分区之间的共享单元层，每个计算分区的节点都被分为两类，一类为普通节点，一类为共享单元层上的节点。共享单元层上的节点可分为该分区的发送块和接收块。通过与其相邻的分区建立对应的发送和接收关系，对通信的发送地址、接收地址和通信数据的类型、数目以及其它通信的信息进行初始化，将相邻分区的通信渠道建立起来。

具体的通信过程如图3a)所示，共享单元层上的a节点和b节点同时为左分区和右分区所共享。左分区只计算a节点，不计算b节点，而右分区只计算b节点，不计算a节点。左分区在求得a节点的位移之后将a节点的位移传递给右分区，右分区的计算同理，如图3b)所示。

图3 共享单元层节点的闭包图

3.2 VerBSS并行算法的流程

VerBSS的并行算法步骤如下：

输入：初始分区网格

输出：变形网格

Step1：初始化分区个数，每个网格分区分配一个进程读取相应的子分区网格。

Step2：查找相邻分区的边界，并在相邻分区中间构建共享区。

Step3：对每个进程读取的子分区网格以及构建的共享区网格进行分类，分为发送块、接收块和普通块，并将每个进程和其它进程要通信的发送地址、接收地址和通信数据的类型、数目等通信信息进行初始化。

Step4：每个进程采用VerBSS算法对该分区进行求解，具体求解过程参见本文2.2节中的VerBSS算法流程。

Step5：在各相邻分区之间进行通信，按照step2建立的通信关系分别进行发送和接收，每个进程将接收到的位移数据整理之后在对应的节点上更新。

Step6：每个进程对更新的位移求位移平方差的平均值，判断其是否满足给定的收敛条件。若满足，则停止循环；若不满足，重复step4和step5，直到满足收敛条件为止。

4 VerBSS并行算法的并行效率分析

本文算例将在一台48核心、128G内存的工作站上进行测试(CPU型号为Inter Xeon(R) E5-2650 v4，主频2.2G)。

4.1 二维模型的算例分析

以一个二维机翼做俯冲运动的模型，其节点数为603 802，单元数为1 203 662。机翼长度为102个单位长度，单元尺寸为1个单位长度，单步旋转角度为0.02。如图4所示为变形前后的对比图。

图4 机翼俯冲变形前后的对比图

采用分区并行的VerBSS算法单步迭代过程中各个步骤的平均耗时和加速比如表1所示。

表1 二维机翼旋转分区并行的单步各步骤耗时

若采用共享式并行的VerBSS算法，单步迭代过程中各个步骤的平均耗时和加速比如表2所示。

表2 二维机翼旋转的共享式并行的单步各步骤耗时

图5为采用共享式并行方案和分布式并行方案时的加速效率对比图。在单个变形时间步的耗时中，矩阵构造时不需要通信，为完全解耦的过程，求解步骤和通信步骤交替进行，其中求解步骤为并行过程，通信步骤为串行过程。在该算例中，当分区数为16时，加速比为15.58，其并行效率为97.37%。当分区数为32时，并行的加速比为26.93，并行效率为84.15%。可见，由二维模型的算例可知，该并行算法在分区数目不超过16时，并行的加速比和理想加速比相当。当分区数目持续增大时，达到收敛条件所需的迭代步数也相应增加，导致并行效率降低，但和共享式的并行方案相比仍然具有较高的加速效率。

图5 机翼俯冲模型变形的加速比

对比普通弹簧法、串行VerBSS算法和本文的并行算法，三种方法变形时网格的最小夹角随时间步的变化如图6所示，可见在算法并行化的过程网格单元的质量具备良好的鲁棒性。

图6 最小夹角随时间步的变化图

4.2 三维网格算例分析

进一步验证本文算法在三维情形中的并行效率，一个三维的机翼在空间中做翘曲变形的网格模型如图7所示。图7a)为8分区的初始网格内部截面图，图7b)为变形后的分区网格内部截面图，其弯曲形状为抛物线型。

图7 三维机翼翘曲变形的流场网格

机翼周围的流场长宽高分别为1 500、500、500个单位长度，网格单元尺寸为0.5个单位长度，该流场网格包含有132 120个节点和656 878个单元，翼尖变形的单步步长为0.5个单位长度。采用分区并行的VerBSS算法迭代过程中各个步骤的平均耗时如表3所示。采用共享式并行的VerBSS算法各个步骤的耗时如表4所示。

表3 机翼翘曲分区并行的单步各步骤耗时

表4 机翼翘曲的共享式并行的单步各步骤耗时

该算例中，当分区数为16时，加速比为13.23，其并行效率为82.69%。当分区数为32时，并行的加速比为21.77，并行效率为68.03%。采用共享式和并行方案和分布式并行方案时的加速效率对比图如图8所示。

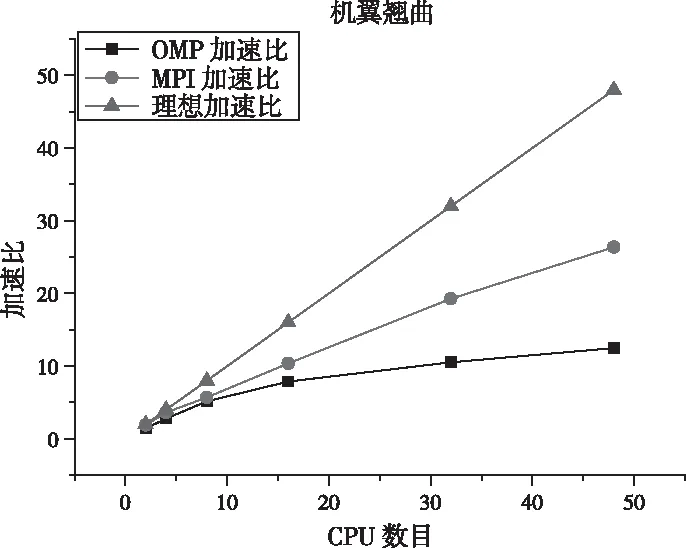
图8 机翼翘曲并行方法的加速比

三维网格不同分区之间的拓扑连接关系也比二维情况也更加复杂，通信过程也更为复杂，导致额外的通信耗时。虽然和二维情形相比，VerBSS并行算法推广到三维情形时，相同的分区数目下并行效率低于二维情形的效率，但该并行算法依然能够保持较高的加速效率，当分区数目为8时，并行效率仍然超过80%。

5 结语

针对弹簧类网格变形方法求解较慢的特点，本文针对基于弹簧类的VerBSS算法提出了一种分布式的VerBSS算法的并行方案。算例结果表明： 基于分区策略的VerBSS并行算法具有良好的并行效率，同时保持了Ball-vertex弹簧单元的抗压能力，变形能力较强，在二维情形和三维情形下都具备良好的适应性。该算法适用于大变形和大规模的网格变形问题。同时，基于分布式的并行方案较共享式的并行架构而言，更适合高性能计算，具有良好的可移植性。