基于交通荷载作用的道路地下塌陷模型研究

付大伟，庄 宇

(1.长春工程学院土木工程学院，吉林 长春 130012;2.佳木斯大学建筑工程学院，黑龙江 佳木斯 154002)

1 引言

随着社会的不断进步发展，城市交通工具越来越多，间接导致道路坍塌事故的发生，不仅威胁到人类的自身安全，还给社会带来巨大的损失。城市中不断增加的交通工具，在其运行过程中会引起周围环境的振动，从而对人类的生活和工作造成长期的影响，如何降低交通环境振动对人的伤害，是交通系统规划过程中首要考虑的问题之一。道路塌陷主要是受交通荷载作用，车辆在行驶过程中是一个多质点的振动系统，当路面不平时，和路面接触的车轮就会按照一定的振幅和频率在路面上跳动前进，从而导致交通荷载大于或小于静载轮载。另外伴随着交通工具行驶速度的快慢，道路路基承受荷载的时间也不相同，即使荷载的作用时间很短暂，累加起来对道路的寿命还是有很大的影响。

目前，作为交通荷载对道路造成塌陷的重点问题，引起很多学者的关注。文献[1]基于卡车的参数统计结果，建立荷载模型，研究荷载的不平稳变化对桥梁结构的影响；文献[2]采用8组模型试验研究荷载类型所造成的路面坍塌情况，在仅有静荷载的情况下，路面坍塌的速度比仅有动荷载的情况要慢，较大的动荷载会加快路面坍塌；文献[3]将交通荷载进行简化处理，利用三角函数与傅里叶变换分析荷载速度、频率等对路面板挠度的影响；文献[4]将交通荷载进行正弦模拟，通过有限元模拟软件进行2维和3维的模拟，研究荷载作用在路面上的规律，计算荷载作用对路面上的影响深度以及动态变化影响。

根据现有研究可知，多数学者将交通荷载转换成静荷载进行研究，使得到的结论与实际路面情况不相符。现实生活中交通负载是包含很多方面的较为复杂的动荷载，因此找到一个合适的模拟方法对交通荷载特性进行分析具有重要的研究价值。于是，本文从交通荷载特性和路面动力特性进行分析，采用Newmark-β直接积分方法对矩阵整体进行求解，由疲劳累计的道路损伤模型，计算出道路相对疲劳损伤度。

2 交通荷载特性及路面动力特性

2.1 交通荷载特性

交通荷载作用在路面上是一个复杂的过程，由于力的相互作用，当交通荷载作用在路面上时，路面结构反过来也会影响荷载的变化。荷载作用在路面上会使路面结构发生变化，引起路基沉降。总而言之交通荷载对路面结构的影响具有一定的特性[5]。当前在全世界的路面设计规范中，交通荷载统一用静止的集中荷载、均布荷载和面状荷载进行表示[6]，用公式可表示为

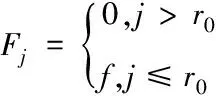
(1)

其中，r0表示交通荷载中心与边界之间的距离；当r0无限趋近于0时，Fj表示为集中荷载；当荷载的作用范围在2r0之内，Fj表示均布荷载；当r0表示为分布半径时，Fj表示面状荷载。交通荷载与车辆在道路上行驶的速度和路面平稳性有关，交通荷载与路面是一种按照椭圆形式接触的压力分布不均匀的荷载路面关系[7]，可以通过简化有限元计算来模拟这种情况。

2.2 路面动力特性

对路面的动力问题进行分析的时候，荷载大小对路面应力的影响可分为3个阶段。第1阶段：若路面形变与荷载成线性关系，那么路面骨架所发生的形变是可以恢复的，这种路面的本构关系可用弹性模型来表示。第2阶段：随着荷载不断增大，会导致路面骨架形变超出弹性形变的范围从而变成塑性形变，整个体系的能量也会不断损耗掉。第3阶段：若路面所受到的荷载超过一定值时，路面孔隙水压力会不断增加，应力不断减小，将会破坏原来的路面骨架结构，从而破坏土体流动性，对路面稳定性造成严重的影响。

在路面结构受到荷载作用发生形变的情况下，对路面地基的本构关系通过软件模拟时，路面的应力不容易实现。因此本文采用数值模拟的研究方法，可以更适用于循环荷载作用下的路面动模量与应变的关系中。

路面应变影响的因素有很多，本文从偏移应力、加荷频率和超固结比等方面对路面应变进行分析研究，通过回归分析方法可以获得路面弹性模量的经验公式，表示为

Te=(a+bτ)(α1R2+β1R+γ1)εe(c+dτ)(α2R2+β2R+γ2)

(2)

其中，a、b、c、d、α1、β1、γ1、α2、β2、γ2表示与初始偏移应力、加荷频率和超固结比相关的参数值。结合试验数据的回归分析，可以求得在不同偏移应力、加荷频率和超固结比条件下的参数值，将各个参数值代入式(2)中，便可以求得路面弹性模量与路面应变的表达式为

Te=(11.88+0.052τ)(-0.16R2+1.48R+0.62)×

εe(-1.49+0.014τ)(0.043R2-0.366R+2.30)

(3)

本文采用此公式模拟道路地面结构层中的路面效应。

3 动力有限元方程的建立

路面结构的外力和位移都可以通过时间函数表示，根据达朗贝尔原理，可以把路面动力学问题转换成每个时间点的瞬时平衡问题。首先把路面结构划分成有限个单元，并将其进行离散化处理。那么单元中的任何一个质点的位移矢量、速度矢量、加速度矢量用公式可表示为

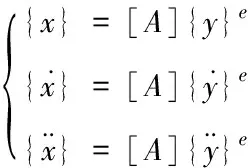
(4)

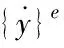
(5)

其中，[G]表示有限单元刚度矩阵；{H}e表示有限单元荷载矢量。有限单元中由集中力、面积力和体积力组成的外力荷载用公式可表示为

(6)

其中，{F}e表示构成有限单元的集中力；∬[A]T{s}dS表示构成有限单元的面积力；∭[A]T{v}dV表示构成有限单元的体积力。有限单元的荷载矢量用公式可表示为

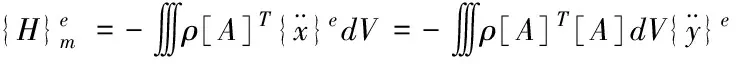
(7)

其中，ρ表示有限单元的密度。交通荷载的振动结构受道路材料阻尼力的作用，且阻尼力正比于速度。设粘性阻尼特性系数用λ表示，那么由阻尼力引起的有限单元荷载矢量用公式可表示为：

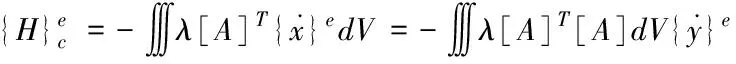
(8)

整个有限单元的荷载矢量用公式可表示为

(9)

将振动结构进行离散化处理，则整体运动方程用公式可表示为

(10)

其中，[M]表示整体质量矩阵；[C]表示整体阻尼矩阵；[G]表示整体刚度矩阵；{H}表示整体荷载矢量。

(11)

根据拉格朗日中值定理，时刻t+Δt的速度矢量用公式可表示为

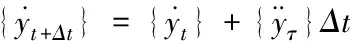
(12)

其中，τ表示时间段的某一时刻。根据Newmark-β直接积分方法，近似值用公式可表示为

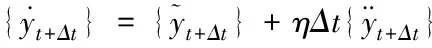
(13)

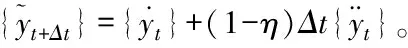
4 交通荷载作用下道路损伤计算

通过有限元模型的计算分析，主要是为了研究交通工具行驶过程荷载的不平稳增长对路面结构疲劳损伤的影响。由疲劳累计的道路损伤模型，路面结构的疲劳性可用公式表示为

RLφ=P

(14)

其中，R表示荷载应力幅值总次数；L表示荷载应力幅值；φ表示道路疲劳强度参数；P表示道路材料疲劳参数。根据线性累计损伤原理可得

(15)

其中，Ki表示道路的疲劳损伤程度；ni表示第i级应力的循环系数；Ni表示第i级应力的疲劳寿命。结合交通荷载对道路结构的疲劳损伤程度，不考虑道路材料疲劳参数的影响，相对疲劳损伤用公式可表示为

(16)

其中，Kp表示道路结构相对疲劳损伤程度；Mi表示第个内力幅值大小；Me表示道路等效内力幅值大小。第i级应力下的等效道路内力幅值用公式可表示为

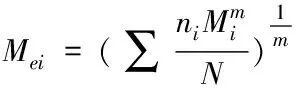
(17)

于是第i级应力下，道路相对疲劳损伤度用公式可表示为：

(18)

本文道路结构采用C50混凝土，预应力筋采用高强度的钢绞线，在路面上选择随机的602个节点，1052个单元。将5种常见的不同轴载的车辆依次驾驶到所选择的道路路面上，从而测出最大弯矩值，如表1所示。

表1 不同轴载下的最大弯矩值

由式(17)并结合表1，可以计算出路面上随机三点的等效应力幅值 ，设三个随机点分别用Me1、Me2和Me3表示，则有Me1=200.255kN·m，Me2=146.380kN·m，Me3=155.725kN·m。

根据偏心压力方法可以计算出路面荷载横向分布参数，测试选取路面上的7个随机点，得到路面的横向分布系数m如表2所示。

表2 路面横向分布系数

结合路面弯矩效应和随机点的横向分布系数，可以计算出各个随机点的最大弯矩值Mi如表3所示。

表3 路面最大弯矩值

由式(18)可以计算出路面的相对疲劳损伤，同时本文对不考率非平稳增长的路面相对疲劳损伤数据结果，与考虑非平稳性的路面疲劳损伤数据结果进行对比，如表4所示。

表4 路面相对疲劳损伤对比结果

由上表可知，在考虑交通非平稳增长的情况下要比不考虑非平稳增长时路面的疲劳损伤更加剧烈，说明交通的非平稳增长对路面的影响很大。

5 交通荷载作用下路面模型分析

本章节依旧选取5种常见的不同轴载车辆，讨论其对道路路面上施加的静荷载稳定性以及路面结构稳定性的影响，为了更符合实际情况，仿真模拟过程中，让重力更大的中后轴应力作用在路面上，分别从位移和应力两方面进行分析。

5.1 位移分析

通过对路面模型进行实验分析，选取不同轴载压力作用下的道路路面上方的节点，并测试节点的竖向位移，如图1所示。由图1曲线可以看出，随着道路路面的水平方向半径的不断增大，路面上测试节点的径向位移也不断增大，当大于5m后，增加速度变快。

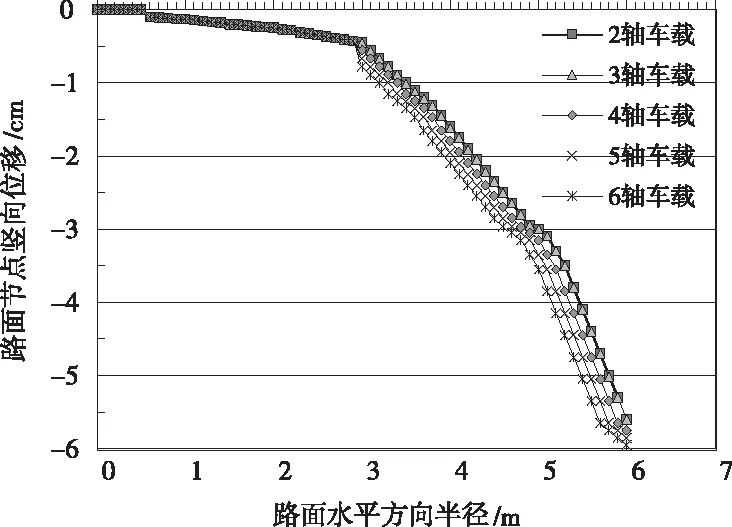
图1 水平方向半径对路面节点竖向位移影响

与此同时，还测试了交通荷载类型对路面上节点的竖向位移影响，如图2所示。由图中结果可以看出，随着交通荷载轴载的增加，车轮对路面的作用力不断增加，路面节点的竖向位移也会增加。当车辆轴载在1-3时，路面节点的竖向位移增加的更快，当车辆轴载大于3时，路面竖向位移趋于平稳，说明对道路结构的影响较小。主要原因是在车辆轴载增加时，车辆有较长的长度，车轴间距离较远，对路面有效影响相对较小。除此之外，还可以看出，动力荷载比静荷载对道路结构稳定性的影响程度要更大。

图2 荷载类型对路面节点竖向位移影响

5.2 应力分析

为了研究道路路面结构的塌陷状态，本文从History命令中选择在5轴车载作用下路面监测节点的最大主应力和最小主应力，研究它们随计算步长的变化情况，如图3所示。

图3 5轴车载作用下主应力变化曲线

从图中可以看出，随着计算步长的不断增加，应力呈现出逐渐平稳的状态；当水平方向半径为2m时，所对应的最大主应力为0.17kPa，最小主应力仍然为负数；当水平方向半径大于3m时，最大主应力已经达到路面结构的抗拉强度最大值6.22 kPa，最小主应力也达到了抗拉强度的最大值1.01 kPa。因此可以得出道路上方节点的路面结构处于不稳定的状态，路面结构有可能继续发生扩展。

6 结束语

为了研究交通荷载所导致的道路地下塌陷问题，本文分别从交通荷载特性和路面动力特性两方面进行分析。根据达朗贝尔原理，

可以把路面动力学问题转换成每个时间点的瞬时平衡问题。然后通过有限元模型的计算分析，研究交通工具行驶过程荷载的不平稳增长对路面结构疲劳损伤的影响。最后选取5种常见的不同轴载车辆，讨论其对道路路面上施加的静荷载稳定性以及路面结构稳定性的影响。通过监测节点证明了本文方法可以准确预测出车辆的非平稳增长对路面所造成的疲劳损伤，当抗拉强度为6.22 kPa时，道路上方节点的路面结构处于不稳定的状态，会导致路面结构继续扩展。