PID控制器中随机干扰控制方法的设计与实现

陈灿辉，黄春庆

(厦门大学航空航天学院，福建 厦门 361005)

1 引言

输出方差是过程控制系统的主要性能指标之一[1，2]。由于PID控制器结构简单易于实现的优点，至今仍然为大多数工业控制回路所采用[4]。受PID控制器结构限制，PID控制器无法完全实现最小方差(Minimum Variance， MV)控制的性能[2，3]。因此，近似实现最小方差控制的PID控制器(MV-PID)参数整定问题是值得研究的问题。

传统的PID参数整定法如Z-N法、继电反馈法、阶跃响应法和极点配置法等[5]，是基于时域的性能指标如超调量、响应时间和调节时间等作为性能指标进行整定参数的，通常把参数整定问题转化为基于性能指标的一个优化问题、并通过求解优化问题获得参数整定。基于最小方差PID控制器参数整定问题也可以采用类似的方法进行求解。Ko和Edgar[6]提出了一种基于过程输出数据和过程模型的梯度基方法来实现最优PID控制器参数整定； Kariwala[7]提出一种解析下界法，通过选择扰动到输出之间的闭环传递函数的两倍时延项脉冲响应系数，来获得PID参数和相应的PID可实现的最小方差；Shahni和Malwatkar[2]提出了一种利用MathWorks优化工具函数fminco实现PID优化设置的简单方法；Huang和Huang[8]提出利用牛顿迭代方法求出PID控制系统的最小输出方差以及相应的最优PID参数。Dickinson和Shenton[9]提出了一种参数空间技术，将现有鲁棒控制技术中的参数空间边界进行叠加，从而实现非保守鲁棒最小方差PID设计。由于最小方差PID控制器参数整定的优化问题是非凸的，因此上述的优化算法对初值选取均有比较高的要求。如果初值选择不当，只能得到局部最优解[3，10]。显然，选择适当的初值并非易事[3]。

针对随机干扰下的MV-PID控制器参数整定问题，考虑其优化问题的非凸性，采用粒子群算法以获取全局最优解。目前，基于粒子群算法的PID参数(PID-PSO)整定方法，基本上是利用PSO的全局寻优特点找到使系统超调量最小、稳定时间最短、上升时间最小等几个描述系统动态性能的指标最优化及系统稳态误差最优的PID控制器参数[11-14]，实际上，对于过程控制系统而言，更关心的是抗干扰的性能。因此本文在利用粒子群算法求解上述提到的非凸优化问题目的在于保证系统稳定的前提下，得到系统的最小输出方差，并用仿真算例验证了本文方法的有效性。

2 MV-PID控制器参数整定

考虑离散反馈控制系统如图1所示，闭环输出可以表示为[3，8]

y(t)=G(q-1)u(t)+N(q-1)a(t)

(1)

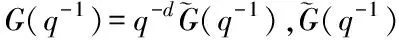
一般地，PID控制器 采用标准离散结构

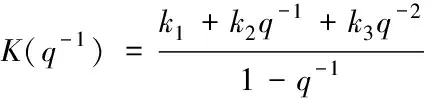
(2)

其中k1，k2，k3为待整定的控制器参数。

图1 典型单回路反馈系统

当参考信号ysp(t)=0时，扰动源a(t)到输出y(t)传递函数表示为[3，8]

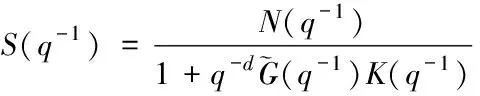
(3)

由于a(t)方差为1，可知系统输出方差为[3]

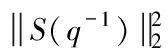
(4)

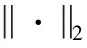
考虑如图-1随机扰动下的过程控制系统，控制器的设计目标是使得闭环系统的抗干扰性能最优。于是，基于最优输出方差性能的PID控制器参数I={k1，k2，k3}整定可表示为如下优化问题

(5)

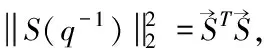
(6)

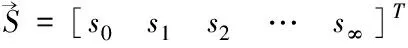
(7)

其中si是闭环传递函数S(q-1)的脉冲响应系数。当S(q-1)的所有极点均位于单位圆内时，对于足够大的i，si将近似于0。事实上，根据文献[2]，当i足够大即i>4d(其中d为受控对象时延)时，式(6)可近似为

(8)

其中

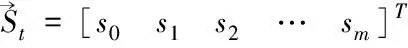
(9)

相应地，优化问题转化为

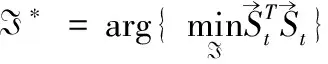
(10)

为了计算方便起见，将控制器中的积分环节与对象模型G合并为

(11)

于是得到如下关系式

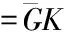
(12)

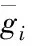
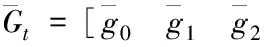
(13)

从而

(14)

其中Nt为扰动传递函数的脉冲响应系数向量，即

Nt=[n0n1n2…nm]T

(15)

W为m×m维矩阵，其中wi为矩阵的第i阶元素

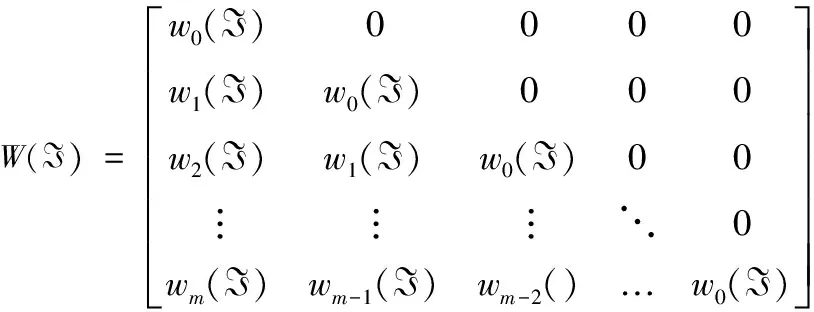
(16)

因此通过求解由式(14)所表征的优化问题(10)，可获得最小方差的PID 控制器最优参数。

3 参数整定优化问题粒子群算法

由于式(10)优化问题的非凸性，传统的凸方法求解往往不能获得全局最优解。考虑到粒子群算法(Particle Swarm Optimization， PSO)具有的优点：搜索速度快，结构简单且易于实现；不依赖优化问题本身的严格数学性质，且能够求得问题的全局最优解，因此在求解MV-PID控制器参数整定问题上比其它迭代优化算法更有优势[15，16]。

给出MV-PID的完整带约束优化问题如下

s.tPL≤k1≤PU；IL≤k2≤IU；DL≤k3≤DU；

(17)

其中PL和PU、IL和IU、DL和DU分别表示PID控制器控制的对应三个参数的约束范围，与此同时，所给的PID参数需要保证系统稳定。

常规的粒子群算法流程主要由以下几个步骤[14，15]：初始化、个体极值与全局最优解、更新速度和位置公式以及终止条件判断。给出各步骤具体内容：

1)初始化：

①确定迭代次数g和种群大小n；

②目标函数的自变量个数d；

2)个体极值与全局最优解：

①定义适应度函数f；

②个体极值为单个粒子找到的最优解，即最小方差；

③从所有种群中找到最优解然后进行迭代更新；

3)更新位置和速度：

速度公式

Vid=ωVid+C1random(0，1)(Pid-Xid)

位置公式：Xid=Xid+Vid

其中ω为惯性因子，其值非负，较大时全局寻优能力强，较小时局部寻优能力强；C1为个体学习因子；C2为社会学习因子；Pid表示第i个变量的个体极值第d维；Pgd表示全局最优解的第d维；Vid表示第i个标量的个体极值第d维的速度；Xid表示第i个变量的个体极值第d维的位置。

4)终止条件：达到迭代次数即终止，否则返回第2)步。

4 仿真算例

本文的仿真，参照文献[3]中提供了十个仿真算例，如表1所示。通过本文所提出的算法求解，获得的最优PID参数整定如表3所示；并将本文的计算结果与文献[3]的结果作对比，相应的最小方差值，均列于表3。具体算法过程说明如下：

表1 仿真算例

通过Matlab仿真软件实现粒子群算法并求解式(10)中的优化问题，其中在搜索空间内随机生成种群时，结合具体系统特征，应保证离散反馈控制系统稳定，即系统的特征方程的根均在单位圆内。在表1算例3，4，5，6中，(在不考虑计算时间开销及计算复杂度的情况下，为了保证整定参数准确性，需要扩大种群的大小)，若是考虑算法的快速性以及结果的准确性，可以将搜索空间M改成：[0， 1]、[-2， 0]和[0， 1]，种群的大小则不需要改变。仿真结果如下：

表2 参数设置

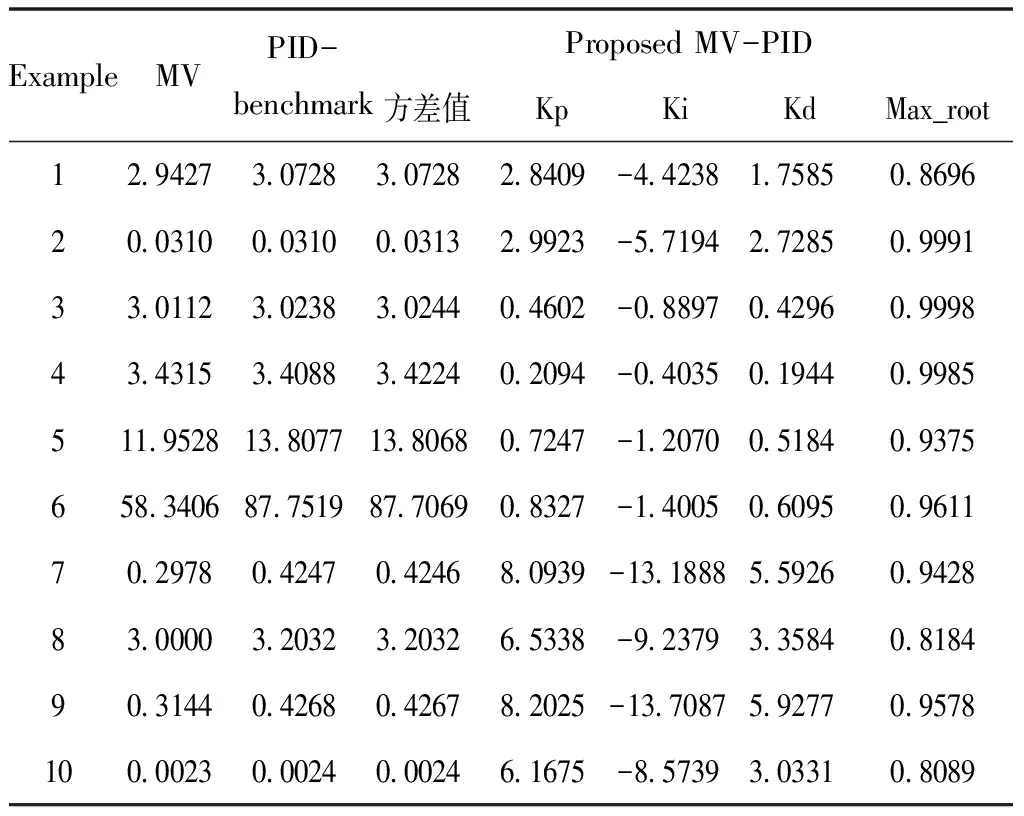
表3 仿真结果比较

表3中，MV表示线性最小方差的理论值；PID-Benchmark表示文献[3]所设计最小方差PID的输出方差值，常常被引为比较基准；本文利用粒子群算法得到结果列于表格右侧，其中列Max_root表示相应的闭环系统特征方程根的最大幅值。

由表3中的仿真结果可见，本文所提出方法获得的闭环系统最终输出方差，与文献[3]的PID-Benchmark，差别几乎可以忽略不计，表明了通过粒子群算法来计算MV-PID参数整定是可行且有效。相较其它的迭代优化算法来说，粒子群算法能够在全局范围内搜索优化问题的最优解，避开局部最优解，使所求解的PID参数在满足系统稳定的前提下，最小化系统的输出方差。

5 结论

当噪声源至闭环输出的传递函数满足稳定条件时，PID参数整定问题可转化为一个非凸优化问题。由于该问题的非凸性，常规优化方法往往无法得到全局最优解。本文采用粒子群算法，获得该非凸优化问题的全局解，从而解决了MV-PID控制器参数整定问题。通过多个仿真算例，应用本文算法进行参数整定，其控制效果几乎与理想最小方差控制一致，从而验证了本文算法的有效性，为MV-PID控制器参数整定问题提供了另外一种值得推荐的选择。