基于FRFT与盲分离的扩频通信LFM干扰抑制仿真
2021-11-17安莎,鲁秋
安 莎,鲁 秋
(1.陕西科技大学镐京学院,陕西 西安 712046;2.陕西理工大学物理与电信工程学院,陕西 汉中,723000)
1 引言
扩频通信具有抗窄带特性,随着扩频增益的增加,通信系统的抗干扰能力也随之增强。扩频通信当前主要应用在卫星通信、卫星导航和军事通信等多种领域[1]。虽然具有良好的通信性能,可以通过增加扩频增益的方法,提高系统的抗干扰能力,然而实际能用的频谱资源有限,大大降低了通信的抗干扰性能提升。随着通信环境和应用场景越来越复杂,通信技术已经成为各国科技竞争的主要领域,因此,研究干扰抑制方法,对于很多领域都具有重要的现实价值。
文献[2]提出一种基于格基约减的扩频通信多址干扰抑制算法,通过格基约减算法对相关矩阵的信号行进正交优化处理,结合多用户检测算法,以简化运算达到对最大似然算法性能的监测。实验结果表明,该算法可以提高扩频通信系统的传输性能,但是通信系统的环境适应性有待增强。文献[3]提出一种直接序列扩频通信系统时变干扰抑制技术,针对时变单音、时变多音和时变多址干扰,推导出理论误码率公式,分析多普勒频移对误码率值的干扰,实验结果表明,该技术提高了频率干扰合并在单载波、多载波中的性能,但在研究过程中没有考虑信道估计带来的影响。文献[4]提出一种基于深度学习的通信抗干扰接收算法,该算法将带有干扰的信号进行预处理,得到可以转化为神经网络进行训练的输入信号,通过感知环境信号,选择合适的算法模块,对干扰进行估计和抑制,实验结果表明,该算法误码性能良好,但在AR干扰随机性增大时,不能对干扰进行有效的抑制。
针对以上研究成果,本文提出了基于FRFT与盲分离的扩频通信LFM干扰抑制方法,建立了三种抗干扰模型,通过盲分离对扩频信号的回波信号和干扰信号进行分离, 基于分阶傅里叶变换,确定目标的回波信号。实验结果表明,本文方法对音频干扰的抑制能力最好。
2 干扰模型建立
2.1 音频干扰模型建立
音频干扰是一种常见的窄带干扰,主要包含具有固定频率正弦波的单音干扰以及具有多个固定频率线性叠加的多音干扰。就扩频通信系统而言,单音干扰更为普遍,音频干扰的时域用公式可表示为
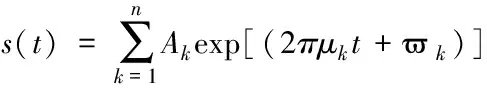
(1)
其中,k表示单音干扰中的正弦频率点;n表示正弦频率点的分量个数;Ak表示频率点的幅值大小;μk表示频率点的频率大小;ϖk表示频率点的初相位。音频干扰的功率可表示为

(2)
2.2 自回归干扰模型建立
自回归干扰是一种通过窄带滤波的白噪声干扰。可以通过信噪功率比求出自回归干扰功率大小。自回归干扰的滤波器是一种全极点的滤波器,其原理如图1所示。

图1 自回归干扰原理
通过滤波器的系数和白噪声都会对自回归干扰的干扰频率、干扰功率等特性造成影响。在传统的自回归模型滤波器计算中,如果滤波器的阶数很大,方程很难求解。因此本文采用递推算法,建立频率和功率均可变的自回归干扰模型,公式表示为

(3)
其中,q表示自回归干扰中全极点滤波器的阶数;Bk表示滤波器的系数;δ(t)表示高斯白噪声。在有高斯白噪声激励的情况下,可以通过全极点滤波器Q(t)产生自回归干扰信号,全极点模型的公式可表示为
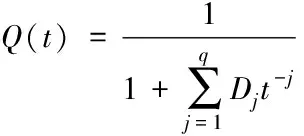
(4)
其中,Dj表示滤波器的滤波系数。进而,可以求出自回归干扰功率谱,用公式可表示为
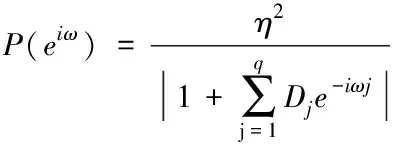
(5)
其中,η2表示高斯白噪声的方差。至此,便能够通过自回归干扰模型产生功率和频率均可变的扩频自回归干扰。
2.3 扫频干扰模型建立
扫频信号对扩频系统的干扰难以消除,是无线领域中一种典型的干扰信号,对扩频系统影响很大,因此对其研究很有必要。扫频干扰频率在一定时间范围内为线性变化,与单音干扰相似。但扫频干扰更为复杂,频率随时间变化较快。扫频干扰的时域公式可表示为

(6)
其中,A~(t)表示扫频干扰的幅值大小;β表示扫频干扰的速率大小;ω表示扫频干扰初始化角频率;γ0表示扫频干扰初始化相位;A*表示当前周期内扫频干扰幅值;T表示扫频干扰周期。通过扫频干扰的速率与周期可以求出扫频干扰的带宽,用公式可表示为
D=βT
(7)
3 盲分离模型
LFM扩频脉冲压缩通信的信号发射模型用公式可表示为[5]
(8)

·exp[j(2πα(t-t1)+πkf(t-t1)2)]
(9)
其中,Ah表示回波信号的幅值大小;t1表示回波信号的延时时间。由于发射信号与回波信号有相关性,转发过程中会导致欺骗干扰[6]。欺骗干扰模型用公式可表示为
+exp[j(2πα(t-t2)+πkf(t-t2)2)]
(10)
其中,Aq表示欺骗信号的幅值大小;t2表示欺骗信号的延时时间,t2的变化速率比t1的变化速率快,是一种循环变化的延时。在有欺骗干扰的情况下,扩频通信的信号接收模型用公式可表示为
j(t)=λ1h(t)+λ2q(t)
(11)
其中,λ1和λ2均表示信号接收系数。由于扩频信号的回波信号和干扰信号在时域和频域上均重叠,通过稀疏理论很难将其分离,因此,盲分离成为了解决问题的关键方法。
假设给定的观测信号矩阵满足G∈Rm×n,将其进行模式分解,公式可表示为[7-8]

(12)
其中,H表示观测信号的混合矩阵;Y表示信号源向量。当m≥n时,因为扩频信号的重叠系统是可逆的,信号源的解有唯一性,所以可以通过盲分离将源信号的时域和频域分离开。
4 基于FRFT扩频通信干扰抑制
FRFT是一种傅里叶变换,傅里叶变换可以同时包含时域和频域,对LFM信号的能量聚集性能特别好。信号的分阶傅里叶变换用公式可表示为

(13)
其中,z(t)表示信号;θ表示FRFT域的旋转角度。假设λ为信号频率,当旋转角度θ=-arccotλ时,则此信号是冲击函数对应的信号。当旋转角度和信号频率不对应时,可通过带通滤波器经过分阶傅里叶反变换求得LFM信号分量。当信号中LFM分量较多时,可通过信号能量多少来获取每个信号的分量。在FRFT域中可以对获得的回波信号以及欺骗干扰信号中各种干扰信号进行分离。然而,当LFM信号的扩频频率大小接近时,会造成不同旋转角度的能量积累,这时不能对回波信号和欺骗干扰信号进行区分,只能对其进行分离。假设LMF信号的斜率抖动值为0,则信号z(t)的分阶傅里叶变换用公式可表示为

(14)
其中,Aθ表示信号z(t)的幅值大小。由FRFT能量的聚集性可知,LFM信号在FRFT域中有最佳旋转角度θm=-arccotλ,当v=0时,Fθm的模有最大值,用公式可表示为

(15)
其中,Tθ表示FRFT的脉冲信号宽度。当信号z(t)的幅值和扩频频率一定时,FRFT的最佳旋转角度为固定值,max|Fθm(v)|与脉冲信号宽度成线性关系。若对信号进行短时分阶变换,需要对其进行加窗处理,加窗函数公式可表示为

(16)
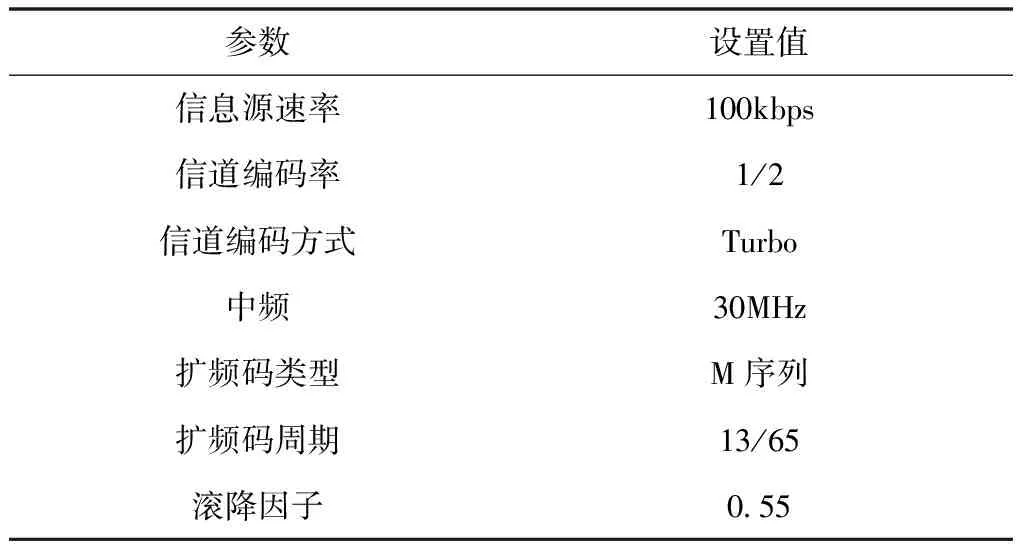
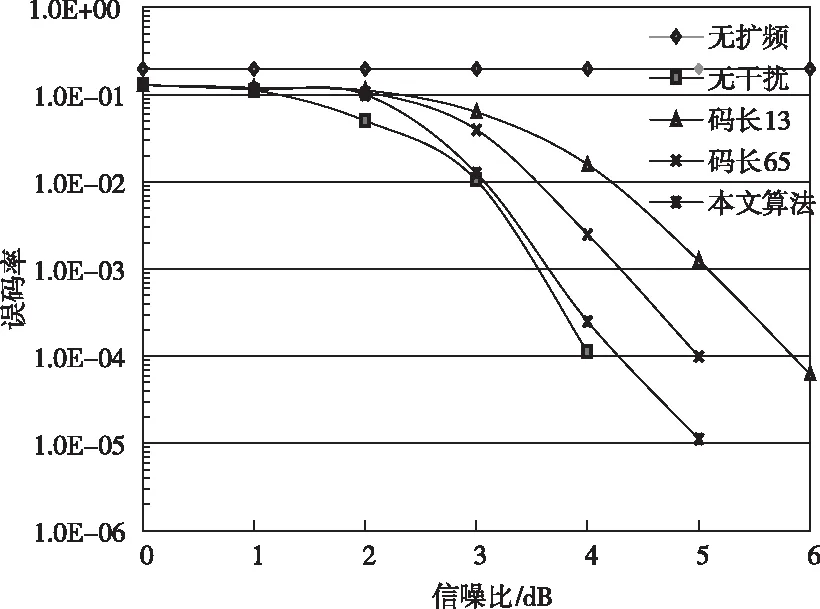
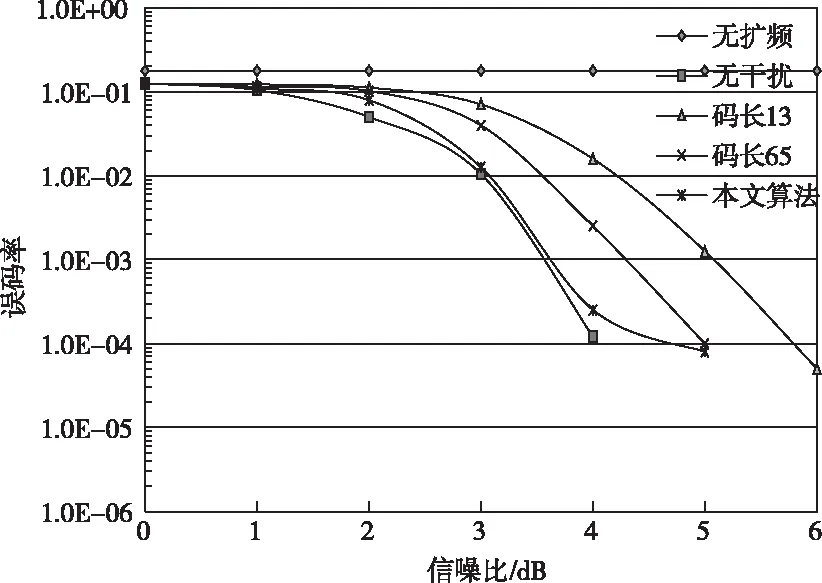
其中,Tv表示加窗函数的宽度,且满足Tv (17) 由上式可知,经过傅里叶变换后,扩频信号的幅值具有最大值,且与脉冲信号宽度无关。利用分阶傅里叶变换对接收信号分离,结合已知回波信号的频率可固定分阶域的旋转角度。如果信号分量的幅值变化不大,那么可通过干扰信号得出信号分量;如果信号分量的幅值变化明显,那么可通过目标信号得出信号分量。为了在FRFT域中使目标回波信号的幅值变化明显,引入加窗系数,用公式可表示为 (18) 其中,t2表示各个信号分量的延时时间;Tc表示最小的发射信号脉冲宽度值。最小周期的信号经过FRFT处理后最大能达到加窗前的1/2,通过信号分离可以确定不断改变干扰信号的延时时间t2,当接收信号峰值较多时,可以通过分阶傅里叶变换,确定目标的回波信号。 为了验证本文所提出方法在三种典型干扰环境下对扩频通信的干扰抑制性能,采用QPSK调制的扩频通信进行误码仿真分析。信噪比区间设置为[0-6]dB,音频干扰载波频率设置为中心频率值,自回归干扰的带宽设置为信道带宽,扫频干扰频率的区间设置为信道的带宽区间。其余参数设置如表1所示。 表1 仿真参数设置 基于本文所提出的干扰抑制算法,在三种典型干扰环境下,采用扩频码周期分别为13和65的误码性能作为对比分析,干扰功率均设置为0dB。 仿真得到音频干扰下的误码性能仿真结果如图2所示。从图中可以看出,本文所提出的算法与扩频通信无干扰情况下的误码性能相近,本文方法在信噪比为4.2dB~4.3dB之间时,误码率即可达到10-4,表明对于扩频信号中的音频干扰,通过本文方法几乎可以全部去除掉。相比扩频码周期为13和65两种情况,本文方法的干扰抑制效果明显更好。 图2 音频干扰下的误码性能 自回归干扰下的误码性能仿真结果如图3所示。从图中可以看出,在无干扰的情况下,信噪比为4dB时,误码率即可达到约10-4;在使用本文方法进行干扰抑制后,信噪比大约4.6dB时,误码率可达到10-4;扩频码周期为65较扩频码周期为13时的抗干扰性能有所提升,但需要信噪比至少为5dB才能够达到10-4误码率。结果表明本文方法能够更好的抵抗自回归干扰。 图3 自回归干扰下的误码性能 扫频干扰下的误码性能仿真结果如图4所示。从图中可以看出,在无干扰的情况下,信噪比为4dB时,误码率即可达到约10-4;在使用本文方法进行干扰抑制后,信噪比大约5dB时,误码率可达到10-4;扩频增益的提高确实能够使通信抗干扰性能有所提升,但在扫频干扰下的提升效果明显不如前述两种干扰环境,扩频码周期为65需要信噪比至少为6.1dB才能够达到10-4误码率。结果结果对比,表明本文方法相比扩频增益,能够更好的抵抗扫频干扰。 图4 扫频干扰下的误码性能 综合仿真结果表明,就音频干扰、自回归干扰和扫频干扰而言,它们对通信的干扰程度不同,且抑制算法对它们的作用效果存在差异,基于FRFT与盲分离的扩频通信LFM干扰抑制方法能够在更低的信噪比情况下,获得更好的误码率,且各种干扰环境下的误码率均明显优于扩频增益方法,充分说明本文方法能够有效抑制不同的通信干扰。 为了提高扩频通信抗干扰能力,本文分析了音频、自回归、扫频干扰模型,并针对LFM扩频脉冲压缩通信问题,对给定的观测信号进行模式分解,基于源信号解的唯一性,通过盲分离将源信号的时域和频域分离开。由于LFM信号能量的聚集性能特别好,因此在信号源旋转角度和信号频率不对应时,通过引入分阶傅里叶反变换求得LFM信号分量,结合加窗处理方法,确定目标的回波信号。实验结果表明,通过本文算法可以有效过滤不同干扰环境下的噪声信号,大大提升信号接受端的抗干扰性能,避免扩频增益对频谱资源的消耗。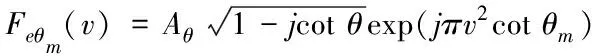

5 仿真结果分析

6 结束语
