高比例光伏并网下火电机组爬坡压力缓解策略

戴 晖，常 平，章 锐，汤 奕

(1.国网淮安供电公司，江苏 淮安223001;2.东南大学电气工程学院，江苏 南京210096;3.哈尔滨工业大学电气工程及自动化学院，黑龙江 哈尔滨 150001)

1 引言

《电力发展“十三五”规划》提出“非化石能源消费比重提高15%以上，煤炭消费比重降低在 58%以下，减小弃风、弃光比例[1]”。自规划发布以来，风电、光伏等新能源装机容量逐渐提高，光伏装机容量持续扩大，截至2018年底，已占全部电力装机容量的9.4%。由于光伏具有较强的随机性、间歇性，且仅在白天发电，与负荷高峰时间不同步，高比例光伏并网使净负荷曲线呈现鸭型，并产生一系列并网问题。美国加州独立运营商(CAISO)将这一现象称为“鸭子曲线”[2-3]。

目前，目前国内外学者主要从源端、需求端等方面对鸭子曲线进行缓解。在源端，主要通过调整光伏电池板的朝向来控制发电量，减少对电网冲击[4]，该方法本质上以牺牲光伏功率换取较小爬坡压力，没有从根本上解决问题。在需求端，主要通过智能终端调节负荷使用方式、用电时间来减小用电高峰时段负荷、增大用电低谷时负荷，使用户参与电网调峰，降低爬坡斜率[5]，但该方法降低了用户负荷供电可靠性。有学者通过引入热电站来缓解鸭子曲线问题[6]，取得一定效果，但光热电站对光伏功率转换效率不够高，在本质上与弃光问题类似，还存在一定不足[7]。上述方法不能从根本上解决鸭子曲线问题，尤其在如何有效缓解火电机组爬坡压力，保障火电机组运行稳定性、火电机组抗扰动能力，提高光伏消纳能力等方面研究还存在不足。

本文在上述研究基础上，首先分析了鸭子曲线问题成因以及给电网调峰调压、火电机组爬坡等带来的挑战。然后通过在高比例光伏并网系统中引入储能电站，构造光储系统，构建数学模型对高比例光伏并网下火电机组爬坡压力进行缓解。数学模型以综合成本最小为目标函数，并在目标函数中增加了火电机组爬坡成本，考虑光伏发电约束、储能约束、火电机组约束、网络安全约束等，构建缓解火电机组爬坡压力数学模型，并利用线性规划单纯形法对模型进行求解。达到平滑鸭子净负荷曲线、缓解机组爬坡压力、保障火电机组安全稳定运行、促进光伏并网消纳目的。最后在IEEE-24节点系统上仿真验证所提策略优越性和有效性。

2 高比例光伏并网问题分析

2.1 问题成因

与风力发电特性不同，光伏发电受日照强度和温度影响，发电功率会在早晨从0开始增加到达一个峰值，然后开始下降，在傍晚时降低到0，在夜间无功率输出。而负荷曲线在傍晚时会逐渐增加，并达到一个峰值。这种发电功率与负荷在时间上不同步带来的负荷与发电功率间差值会产生净负荷曲线，在形状上与“鸭子”类似，如图1所示。在凌晨至清晨时间段，净负荷曲线波动较为平缓。从清晨开始，随着光伏功率的升高，净负荷曲线开始快速下降，在中午时刻达到最低点。清晨至傍晚时间段曲线被称为“鸭肚”。在傍晚时分，随着光伏功率的减小，净负荷曲线开始陡然升高并达到最大值，该段时间曲线被称为“鸭脖”。美国加州独立运营商(CAISO)将其称为“鸭子曲线”。我国淮安金湖县正创建国家高比例可再生能源示范县[8]，到2020年光伏装机达500MW以上，届时光伏并网也会产生类似“鸭子曲线”现象。

图1 CAISO预测的鸭子曲线发展趋势[2]

随着光伏并网比例的增加，白天“鸭肚”将更大，傍晚“鸭脖”将更长，如图1所示。这种大肚腩、长脖子的鸭子曲线将降低电压质量、增加机组爬坡压力。其它机组功率需要在清晨时刻迅速下降，在傍晚时刻快速上升，迅速达到峰值，才能满足电网供需平衡，给其它机组安全稳定运行带来巨大压力。

2.2 高比例光伏并网带来的挑战

鸭子曲线将进一步放大光伏功率的随机性和波动性，增加系统运行难度和规划的不确定性，影响系统其它机组运行特性[9]。现有电网以火电机组运行为主，火电机组运行特性[10]如图2所示。

图2 常规火电机组发电调节特性

若某台机组从时刻1开始并网发电到时刻4与电网解列，则其发电功率范围如曲线形成的面积所示。时刻1到时刻2阶段为机组开机过程，时刻5到时刻6为机组停机过程，都没有调节能力。从时刻2到时刻5机组处于正常运行状态，可以在梯形BCDE内任意一点运行。但机组最大上坡率不能超过斜线BC，最大下坡率不能超过DE。随着光伏并网比例的提高，鸭子曲线峰谷差将持续扩大，火电机组下坡能力、上坡能力可能无法响应其变化[11]。电网难以维持功率平衡、系统电压或频率也无法满足要求，影响电网安全稳定运行。

3 火电机组爬坡压力缓解策略

3.1 光储系统结构

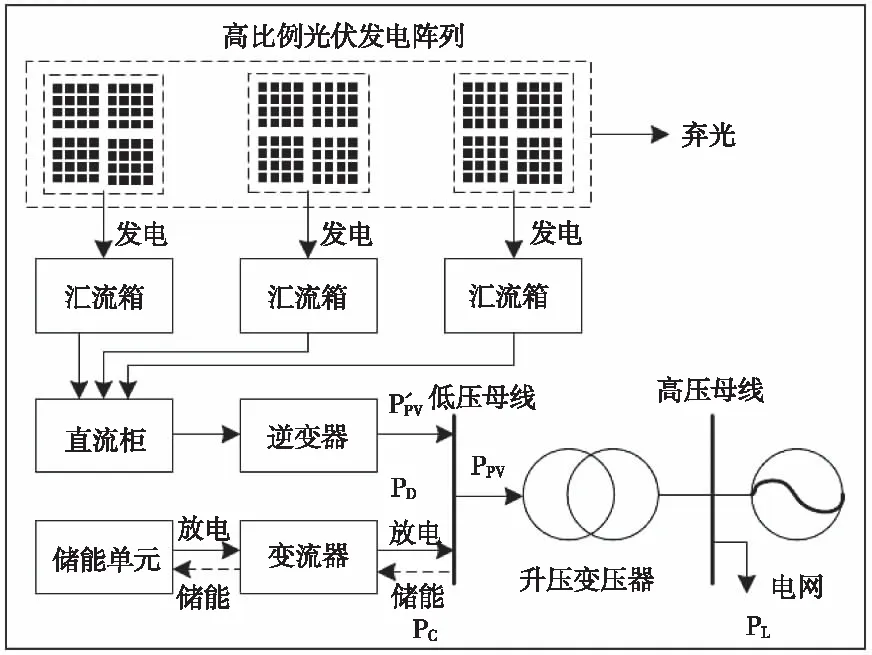
图3 光储系统结构

本文思路是在白天光伏并网比例达到一定值后，由储能系统进行储能，储能功率为PC，减小光伏直接并网功率，抬高白天净负荷曲线，减缓净负荷曲线变化速度。在夜间负荷高峰时段，由于光伏发电功率为零，由储能系统进行放电，放电功率为PD，拉低夜间净负荷曲线，缓解净负荷变化速度，如图4所示。通过减缓高比例光伏并网引发的鸭子净负荷曲线变化速度，平滑净负荷曲线，进而达到缓解火电机组爬坡压力的目的。鸭子曲线功率PY计算如式(1)所示

(1)

式中PPV为光储联合出力，PL为负荷。

图4 机组爬坡压力缓解思路

3.2 缓解火电机组爬坡压力数学模型

基于搭建的光储系统结构和火电机组爬坡压力缓解思路，以平滑鸭子净负荷曲线、缓解火电机组调峰压力、提高光伏消纳能力为目标，构建缓解火电机组爬坡压力数学模型。

3.2.1 目标函数

综合考虑弃光、储能与发电机的调节能力，以光储系统综合运行成本最小为目标，目标函数如式(2)所示

(2)

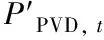
3.2.2 约束条件

约束条件主要包括有用平衡约束、光伏发电约束、储能约束、火电机组约束、线路约束以及失负荷约束。

1)有功平衡约束。系统有功率要满足平衡条件。如式(3)所示

(3)

式中，PLj，t为第j个负荷节点t时刻负荷功率，PPV，t为t时刻光储联合出力。

2)光伏发电约束。主要包括运行约束、爬坡约束以及弃光约束。具体如式(4)所示

(4)

3)储能约束。主要包括储能功率约束、储能荷电率约束以及储能容量约束。储能功率约束如式(5)所示

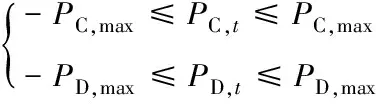
(5)

式中PC，max为储能最大充电功率，PD，max为储能最大放电功率。

储能荷电约束如式(6)所示，设置此项约束可以避免储能过充、过放。

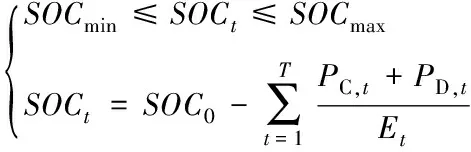
(6)

式中SOCmax、SOCmin为储能最大、最小荷电率，SOC0为储能系统初始荷电率，Et为储能容量。

储能容量约束如式(7)所示，确保储能每时每刻的储能容量满足要求。

(7)

式中，EMax，EMin分别为储能容量上下限(这里分别取100%的额定容量与10%的额定容量)，Δt为时间间隔，η1，η2分别为储能放电与充电的效率。

4)火电机组约束。主要包括运行约束和爬坡约束，如式(8)所示

(8)

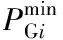
5)线路约束。主要包括线路功率等式约束、线路传输功率约束和节点相角约束。如式(9)所示

(9)

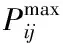
6)失负荷约束。即系统中某节点的失负荷功率不能大于该节点负荷功率。具体如式(10)所示

0≤PLDj，t≤PLj，t

(10)

3.3 线性规划单纯形法

缓解火电机组爬坡压力数学模型包括：目标函数、等式约束条件、不等式约束条件、上下限约束条件以及求解变量。该数学模型是一个标准的线性规划问题，故本文基于线性规划单纯形法对模型进行求解[13]。缓解火电机组爬坡压力的线性规划模型如式(11)所示

(11)

结合缓解火电机组爬坡压力数学模型，式(11)中变量具体如(12)所示

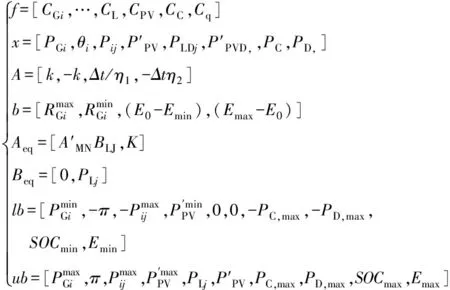
(12)

式中f为成本，包括机组运行成本、机组爬坡成本、失负荷成本、弃光成本、储能运行成本。x为待求量，包括机组输出功率、节点相角、线路有功功率、光伏发电功率、失负荷功率、弃光功率以及储能充放电功率。A为系数矩阵，包括机组爬坡功率系数矩阵(一般取K=[K]，k=±1)、充放电功率系数矩阵。b为不等式约束向量，包括机组上下爬坡率，充放电约束。E0为储能系统初始时刻功率。Aeq为等式系数矩阵，包括线路有功等式约束、系统功率平衡约束系数矩阵。BIJ=[Bij]。Beq为等式向量矩阵，包括线路有功等式向量、系统负荷功率向量。ub、lb分别为火电机组发电功率、节点相角、线路热稳定功率、光伏发电功率、负荷功率、弃光功率、储能充电放电、储能荷电率、储能容量的上限、下限向量。基于单纯形法求解时一般遵循以下步骤：确定初始基可行解，检验所得到的基可行解是否最优，迭代求新的基可行解。

3.4 火电机组爬坡压力缓解策略

基于根据构建数学模型和线性规划单纯性求解算法，构建火电机组爬坡压力缓解策略，如图7所示。具体如下：

1)设置成本参数火电机组CGi、失负荷成本CL、弃光成本CPV、储能成本CC，机组爬坡成本Cq，储能容量E0，时间T等。

3)准备线性模型中参数，如成本向量f′。火电机组爬坡功率系数矩阵A。火电机组上下爬坡率及充放电约束向量b。线路有功等式约束和系统功率平衡约束系数矩阵Aeq。线路有功等式向量，系统负荷功率向量Beq。火电机组发电功率、节点相角、线路热稳定功率、光伏发电功率、负荷功率、弃光功率、储能充电放电功率、储能荷电率、储能容量上限，下限向量ub，lb。

4)由上述矩阵和向量，构造缓解火电机组爬坡压力线性数学模型。

5)设置或更新模型的初始可行解X(t)=(b1，b2…，bm，0，…，0)′，并计算校验数δj，若δj≤0则计算下一时刻t=Δt+t的最优解。

6)δj中有一个大于零，则计算换入变量xk，换出变量xl，更新初始可行解，并进行迭代、检验计算，直到得到最优可行解。

7)若所有时刻均求出可行解，则输出最优解。具体如图5所示。

图5 火电机组爬坡压力缓解策略

4 算例分析

4.1 仿真系统搭建

为了验证本文所提策略的优越性和有效性，借助MATLAB搭建了IEEE-24节点系统，并对其进行改进，改进后的系统结构如图6所示，对上述缓解火电机组爬坡压力线性数学模型进行仿真分析，验证本文构建的光储系统和数学模型可以缓解高比例光伏并网带来的火电机组爬坡压力问题，促进光伏消纳。IEEE-24节点系统中火电机组的出力功率范围如表1所示，爬坡率取为每分钟调节2%的最大出力，采用对比分析：

策略1：只在原系统19节点并入光伏电站；

策略2(本文所提策略)：在策略1的基础上再在19节点上接入储能系统。

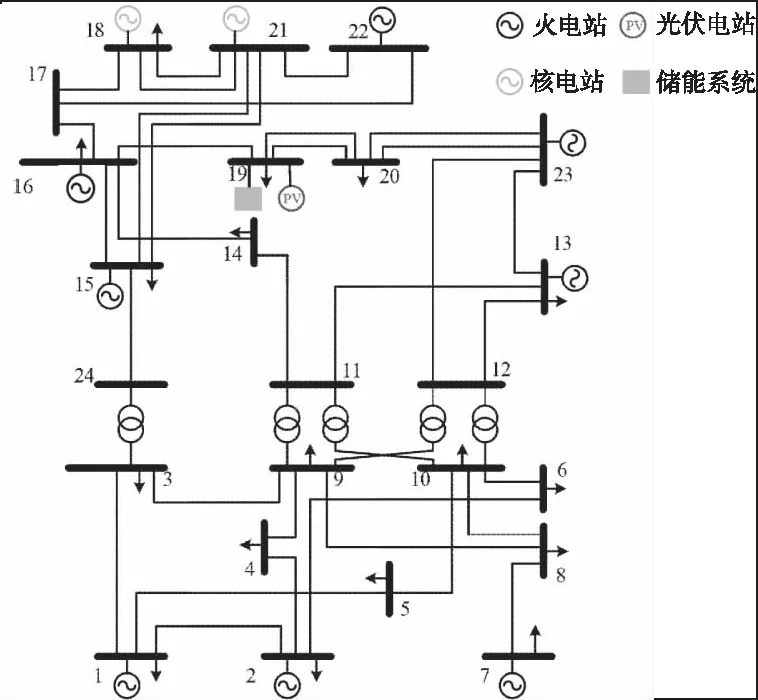
图6 改进的IEEE-24节点系统结构

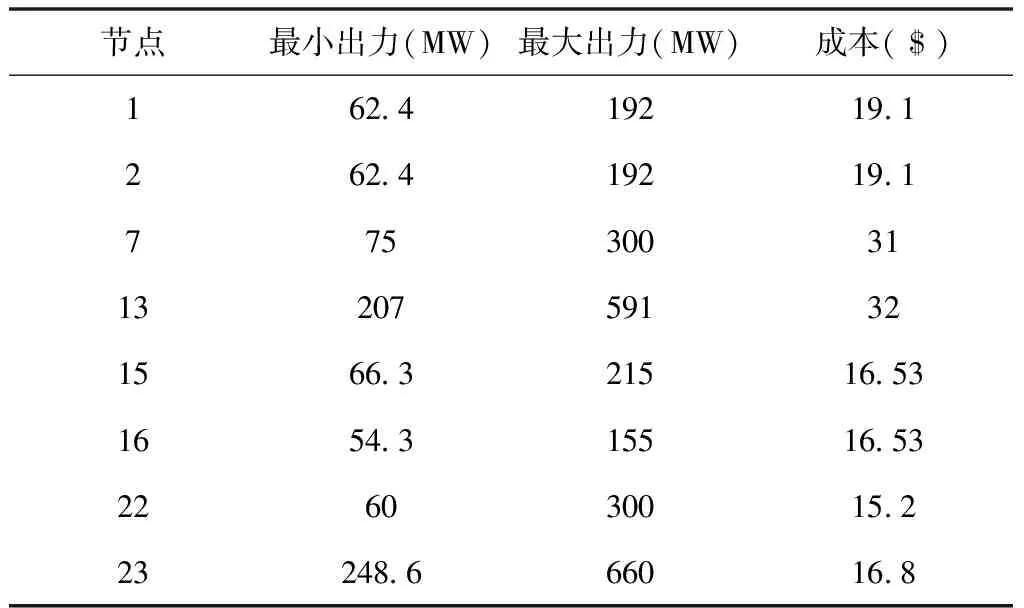
表1 火电机组出力功率及成本数据

各节点的负荷随时间变化，总负荷预测功率和光伏预测功率如图7所示，数据参考2016年10月22日加利福尼亚负荷与与光伏数据。爬坡率上、下限均为20MW/min，储能系统运行成本系数为9$/MWh。弃光惩罚系数为11$/MWh，失负荷惩罚系数为1000$/MWh。火电机组爬坡成本因子取25。

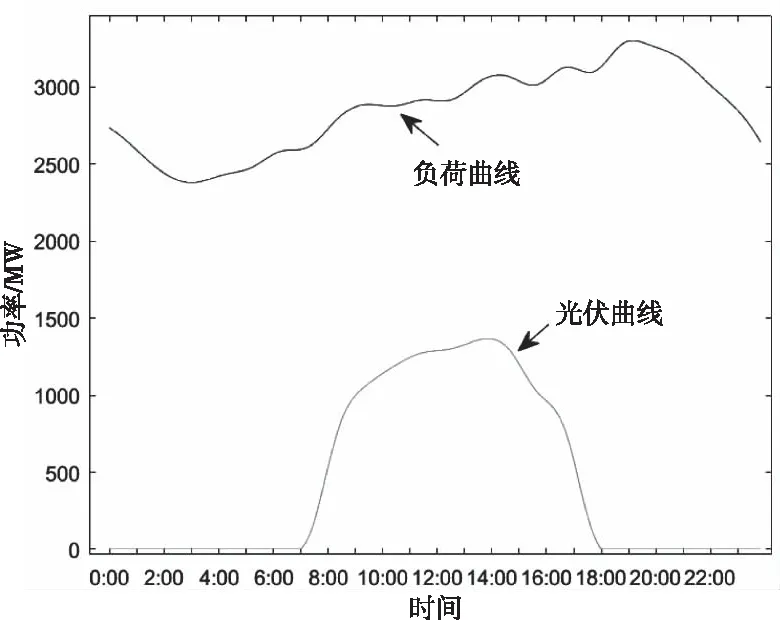
图7 总负荷和光伏预测功率

本文基于图5所示的火电机组爬坡压力缓解策略，借助线性规划单纯形算法，利用MATLAB对模型进行求解。结果如下。

4.2 方法优越性分析

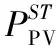
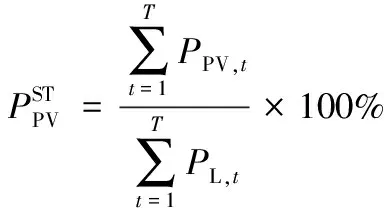
(13)

光伏渗透率计算结果如图8、图9所示。由图可以看出，各光伏发电比例下策略2的弃光功率均低于策略1，策略2的光伏渗透率高于策略1。这是由于策略1仅依靠传统火电机组消纳高比例光伏功率，而火电机组爬坡能力有限，为保证系统稳定运行，不得不丢弃部分光伏功率。策略2的光储系统对高比例光伏功率进行适当地储能和放电，减小弃光功率，使其可以更多的被火电机组消纳。

按比例逐渐增加图7中光伏预测功率，分别对策略1、策略2下的光储系统综合成本进行求解，结果如图10所示。由图可以看出，不同光伏并网比例下，策略2的综合成本始终低于策略1。这是由于策略1的弃光功率、机组爬坡压力均比策略2高，导致策略1的弃光成本、机组爬坡成本高于策略2。与策略1相比，本文所提策略2有效降低了光储系统综合成本，提高系统运行经济性。

图8 弃光功率曲线

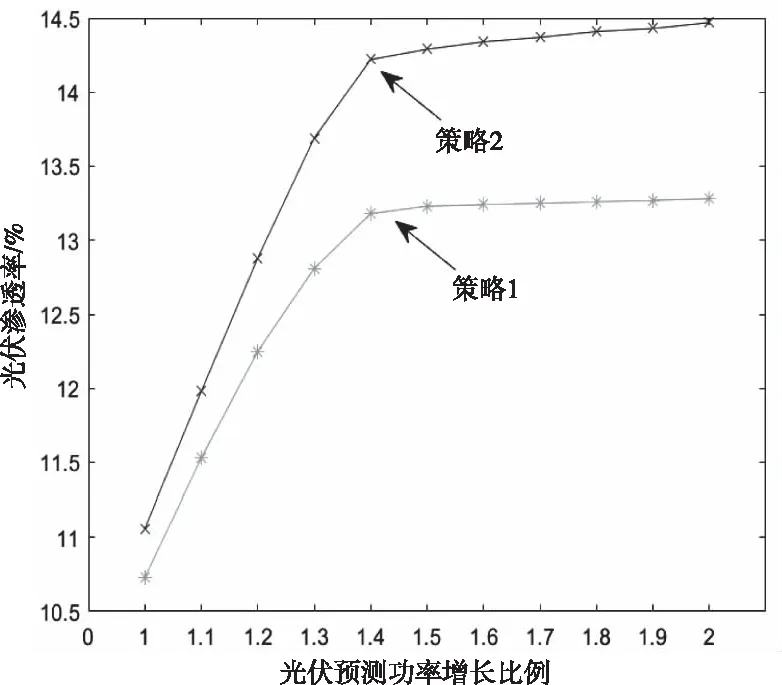
图9 光伏渗透率曲线

图10 光储系统综合成本曲线

4.3 方法有效性分析

经过上述仿真验证可知，策略2的方法优于策略1，在减小弃光功率、提高光伏消纳水平、降低系统综合成本上具有一定优势，下面进一步分析策略2的方法有效性。在光伏发电比例1.4的情况下，对策略2的鸭子净负荷曲线进行求解，如图11所示。

图11 鸭子净负荷曲线

由图11可以看出，策略2得到的净负荷曲线与原始净负荷曲线相比在整体上较为平滑，曲线波动性也相对较小。这是由于策略2的储能系统在光伏发电功率高发时段进行储能，在光伏发电功率低谷进行放电产生的效果，策略2在平滑鸭子净负荷曲线上具有一定的效果。

进一步对原始净负荷曲线及策略2净负荷曲线对应的机组爬坡率进行求解，结果如图12所示。由图12可以看出，在早上8：00和晚上17：00，原始净负荷曲线对应的机组爬坡率均出现峰值，而策略2在此时间段分别对其进行了有效的缓解，减小对火电机组爬坡的压力。这是由于储能系统在早上6：00-8：00时间段放电补充光伏发电功率，在8：00-17：00时间储能消纳光伏过剩的发电功率，在17：00-20：00时间段又放电补充光伏发电功率的不足产生的效果。净负荷曲线的下坡和上坡时段功率得到平滑后，可有效减小火电机组的爬坡压力。具有重要的工程应用价值。

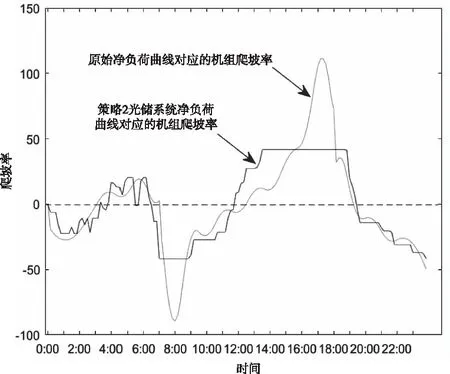
图12 净负荷对应的机组爬坡率

5 结论

高比例光伏并网使净负荷曲线在白天出现极低的谷值，净负荷波动幅度加大，火电机组不能及时响应净负荷波动，爬坡压力极大，危及电网安全稳定运行。本文搭建的光储系统结构、构建的缓解火电机组爬坡压力数学模型以及提出的火电机组爬坡压力缓解策略，可较好的平滑鸭子净负荷曲线、有效缓解火电机组爬坡压力，在减小光伏弃光率、提高光伏消纳能力、缓解调峰压力的同时，保障了火电机组的安全稳定运行能力、抗扰动能力，对保障电网安全稳定运行具有重要的学术研究意义和工程实用价值。