基于数据挖掘与小波去噪的短期风电功率预测

2021-11-17陈中慧王海云王维庆武家辉

计算机仿真 2021年9期

陈中慧，王海云，王维庆，武家辉

(新疆大学电气工程学院，新疆乌鲁木齐 830047)

1 引言

为了应对化石能源枯竭以及化石能源带来的环境污染问题，世界各国正在大力开发可再生能源。风能是可再生能源的重要组成部分，得到了大力发展。由于风的波动性与间歇性使得大规模风电并入电网时给电力系统安全稳定运行以及电力调度部门带来了巨大挑战。当前，风电功率预测是解决该问题的重要手段[1]。

风电功率预测按时间尺度的不同可分为长期(以年为单位)风电功率预测、中期(3-7天)风电功率预测、短期(1-72小时)风电功率预测[2]。短期风电功率预测便于电力调度部门制定合理的电网调度策略，保证供电质量[3]。目前，风电功率的预测方法主要有人工神经网络法(artificial neural netwoks，ANN)，时间序列分析模型法、支持向量机(support vector machine，SVM)等。其中ARMA是时间序列分析法中高级的预测方法，具有较好的预测精度[4]。文献[5]运用改进的牛顿算法LM优化BP神经网络参数形成LM-BP模型进行风电功率预测，将预测结果与BP神经网络进行比较，证明LM-BP的优越性，最后用时间序列法ARMA对预测风电功率序列进行误差修正，取得了较好的预测效果，但是对于建模所需的风电数据并未做深入挖掘处理使得风电数据质量不高，影响预测精度需要加入ARMA误差校正，使得预测模型复杂。文献[6]采用改进K近邻算法(improved K nearest neighbor，IKNN)，进行风功率预测，根据预测结果进行风水协同运行次日计划，并加入风功率实时预测对计划数据进行修正以减少预测误差，实现实时协同控制运行。但在风电预测环节并未对历史风速与风电功率数据进行处理，导致在次日风水协同计划中加入实时预测来进一步提高风电功率预测精度。文献[7]利用信息熵对预测模型的输入输出量进行高关联度样本筛选，充分挖掘风电数据之间的关系，提高建模数据质量，然后采用粒子群PSO优化Elman神经网络进行风电功率预测，结果证明经过信息熵处理的风电功率预测取得了较好的预测效果，但是熵相关系数求解较复杂，高关联度没有统一的标准值。文献[8]利用经验模态分解(EEMD)对风速进行分解，然后对每个风速子序列预测建立最小二乘支持向量机(LS-SVM)模型进行预测，之后将风速预测结果叠加。同样文献[9]利用小波分析分解风电功率，之后对不同风电功率分量分别建立相应的径向基神经网络模型进行风电高功率预测，最后重构各分量预测结果。文献[8]与文献[9]需分别对每个分解的风电子序列建模，使得风电功率预测模型复杂且消耗大量计算。影响风电功率预测效率。

综上，本文提出了基于数据挖掘与小波去噪的短期风电功率预测模型。通过应用曲线拟合方法修改异常数据、填补丢失数据，解决了一些未采用数据挖掘技术的风电功率预测所导致的预测精度不高需要添加ARMA进行误差较正的问题。且曲线拟合方法建模简单，计算量小改善了信息熵数据挖掘方法建模复杂难求解的问题。应用小波变换法消除风电数据中的噪声降低了风电数据的波动性，以期进一步提高风电功率预测精度。本文重构经过处理的风电功率序列建立单个ARMA预测模型与应用EEMD、小波分析法分解风电序列建立多个预测模型相比，简化了风电预测模型，大大减少了计算量。最后，经过算例仿真分析验证了所述方法有效的提高了风电功率预测精度。

2 数据预处理

2.1 数据挖掘

随着数据收集和存储技术的进步在风电领域产生了海量数据，为了提取海量风电数据中的有用信息，在风力发电背景下的数据挖掘技术得到了广泛应用[10]。数据挖掘是对大量且粗糙的数据进行处理，挖掘数据中隐含的有用信息的过程[11]。本文采用多项式曲线拟合法拟合出风速-风电功率曲线图，挖掘出隐藏在历史数据中风速与风电功率的内在联系。曲线拟合的原理就是寻找与给定点的距离平方和为最小的曲线。多项式曲线拟合[12]的原理如式(1)，(2)所示

(1)

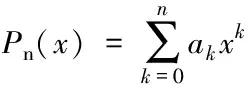
(2)

式中f(x)为拟合多项式函数；Pn(x)为多项式函数；(xi，yi)为给定数据点；ak为系数。n为多项式阶数。当满足式(1)时，便可求出拟合曲线f(x)。

2.2 小波去噪

小波变换(wavelet transform，WT)具有局部变换的思想又克服了傅里叶变换窗口大小不随频率变化等缺点，能够提供一个随频率改变的“时间-频率”窗口，是进行信号时频分析和处理的理想工具[13]。风电数据在采集时会受到噪声的污染，小波变换将风电功率信号分解为低频部分和高频部分，噪声多包含在高频部分中，需对高频部分设置阈值，滤除高频部分中包含的噪声，然后对分解的低频部分与经过去噪处理的高频部分进行重构即进行小波逆变换，达到小波信号去噪的目的。本文采用离散小波变换分解风电功率时间序列f(t)，其公式如式(3)所示

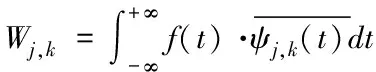
(3)

式中j为位置范围，k为采样时间，Ψj，k(t)为小波函数，Wj，k为离散小波变换的系数。

离散小波变换的重构公式(逆变换)如式(4)所示

(4)

式中C为与信号无关的常数。y(t)为经过小波去噪后的风电功率序列。

3 ARMA预测模型

时间序列法常用于短期的风电功率预测，利用适当的时间序列模型输入风电场的输出风电功率便可以进行风电功率的输出预测。自回归移动平均(ARMA)模型、移动平均(MA)模型以及自回归(AR)模型是常见的时间序列模型[14]，其模型结构如式(5)所示

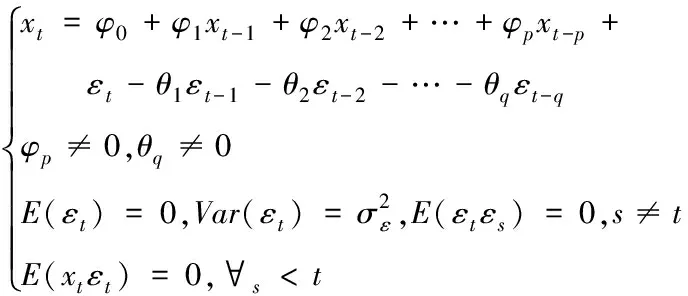
(5)

式中xi为原始序列；φi和θi为模型参数；p为AR(自回归模型)阶数；q为MA(移动回归模型)的阶数。由上式可以看出当ARMA模型的p，q为特定值时，即p=0时，ARMA模型变成了AR(p)模型；q=0时，ARMA模型变成了MA(q)模型。

时间序列预测法的输入量要求为平稳序列，因此在应用ARMA模型预测风电功率是应首先判断输入的风电功率是否为平稳序列。本文利用增广迪基-福勒ADF(Augmented Dickey-Fuller)单位根检验[15]判断风电功率时间序列的平稳性。ADF的3种检验模型公式如式(6)(7)(8)所示

(6)

(7)

(8)

式中t为时间变量，ΔXt为t时刻的残差；X(t-1)为t-1时刻的残差；βt为趋势项；α常数项；εt为残差项。从式(6)开始检验，假如检验不满足H0：δ=0，表明原序列不存在单位根则原序列为平稳序列，检验终止，反之继续式(7)的检验，直到式(8)为止。若经过式(8)的检验，原始序列依然存在单位根则序列为非平稳时间序列需对其进行平稳化处理。

在对输入ARMA模型的输入时间序列进行平稳性判断之后，需要确定ARMA模型的p，q值，本文采用Akaike Information Criterion(AIC)准则对模型ARMA(p，q)定阶。当AIC函数取得最小值时，ARMA模型便认为取得最佳模型。AIC准则函数[16]公式如式(9)所示

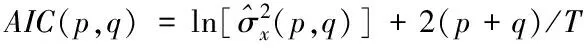
(9)

(10)

本文采用Yule-Walker方程[17]确定模型的自回归参数φp计算公式如式(11)所示：

(11)

式中φp为自回归参数，ρ为模型的自相关系数。

应用矩估计法估计移动平均参数θq，模型的自协方差函数和移动平均参数θq的关系如式(12)(13)所示

(12)

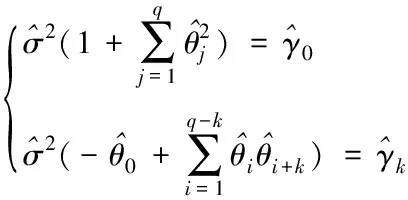
(13)

且1≤k≤q，式中σ2为方差，γ为协方差。

图1为本文模型的流程图，首先对数据进行预处理，其次采用ARMA进行风电功率输出预测。

图1 建模流程图

4 算例分析

本文采用国内西北某风电场2018年1月1日至1月31日的风速、风电场输出风电功率为原始数据，数据采样间隔为15min，共计1514个数据点。对未来2018年2月1日00：00到2018年2月1日2：45的12个数据点进行风电场输出短期风电功率预测。

首先根据历史风速与风电场输出风电功率数据进行多项式曲线拟合，拟合曲线如图2。

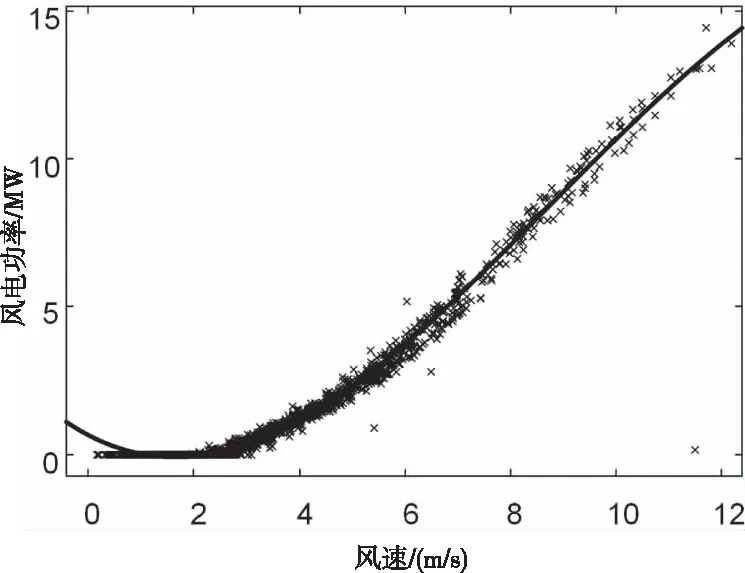
图2 多项式拟合曲线

大量历史风电数据含有一些错误的数据，如风速为零时输出风电功率不为零或者风电功率、风速为负等，以及丢失部分数据，直接应用原始风电功率往往达不到较好的预测效果，由图2多项式拟合的曲线知，若风速值小于3m/s，则风电出力为零;若风速值大于3m/s，便可以通过多项式拟合曲线更正错误的风电功率值。当风电功率有误时，可根据风速利用拟合曲线计算风电功率;当风速错误时根据风电功率计算风速值。对于历史风电数据中丢失的数据可用前一天以及后一天此刻的平均值代替。然后将经过多项式拟合曲线处理的风电功率序列进行小波分解。结果如图3。

图3 小波分解结果

噪声包含在高频部分中，对高频部分设置阈值滤除噪声后与低频部分重构，只经过多项式拟合曲线修正的风电功率与加上小波去噪的风电功率结果对比如图4。经过小波阈值消噪后的风电功率波形较为平滑，可以更好的展现风电功率的变化趋势。

将经过小波去噪的风电功率时间序列作为ARMA模型的输入时间序列。本文采用ADF判断输入风电功率时间序列的平稳性，其结果见表1。

表1 单根检验

由表1的结果可以看出，ADF的统计值为-8.04524，小于10%水平下的临界值-2.14861，这表明在10%显著水平下拒绝风电功率时间序列存在单位根的假设，可认为风电功率时间序列为平稳时间序列。

图4 消噪结果对比图

ARMA模型的输入风电功率时间序列自相关图和偏相图如图5。

图5 风电功率的相关性检验

图5展示出了风电功率时间序列的自相关(Autocorrelation)与偏相关(Partial Correlation)柱状图以及与其对应的自相关系数值(AC)、偏相关系数值(PAC)，由图5可以看出自相关与偏相关柱状图均存在拖尾现象，自相关柱状图在3阶之后均在虚线之内，即q=3。偏相关柱状图在2阶之后均在虚线之内，即p=2。可初步确定模型阶数ARMA(2，3)。为进一步确定ARMA模型阶数，AIC的计算值见表2。

表2 各模型的AIC值

由表2可知当模型复杂度升高时，AIC函数值基本呈下降趋势，但是当复杂度过高时，AIC函数值反而增大，当p=2，q=3时，根据AIC函数值最小原则，确定ARMA最佳模型即ARMA(2，3)。

利用上文中第3节的Yule-Walker方程确定模型参数，结果如表3所示。

表3 ARMA模型参数值

将经过数据挖掘处理以及小波去噪的1514个风电功率数据作为ARMA(2，3)模型的训练样本。

为了验证本文模型在预测精度方面的优势将本文预测模型的预测结果与未经数据处理的传统ARMA模型的预测结果与应用较广泛粒子群优化BP神经网络(PSO-BP)模型预测结果对比，如图6。

图6 不同预测模型结果对比图

由图6可以看出各预测模型均有较好的预测趋势，传统ARMA预测模型随着预测步数的增加预测精度降低。但本文预测模型比较贴近实际值。

为了定量的分析不同预测模型的精确度，本文引用了MAPE(平均绝对百分比误差)、RMSE(均方根误差)、MAE(平均绝对误差)进行误差分析，其计算公式如式(14)-(16)所示。结果见表4。

(14)

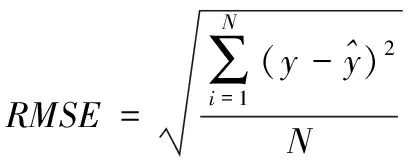
(15)

(16)

式中N表示样本容量，y表示实际风电功率，表示预测风电功率。

表4 各预测模型的误差评价指标

由表4可知，本文模型的平均绝对百分比误差比传统的ARMA模型降低了9.44%，比PSO-BP模型降低了10.35%；本文模型的其它两种误差指标均小于传统ARMA模型与PSO-BP模型。证明了用于建模的风电数据质量对预测精度的影响。在进行风电功率建模前对风电数据进行数据挖掘与去噪能显著提高风电功率预测精度。