概率计算神经网络硬件架构
2021-11-17陈宇昊宋印杰祝亚楠高云飞李洪革
陈宇昊,宋印杰,祝亚楠,高云飞,李洪革
北京航空航天大学 电子信息工程学院,北京100191
目前,传统的冯诺依曼架构的中央处理器芯片占据着计算处理的核心。冯氏架构通过存储、计算和控制单元独立运行、分工配合完成运算任务,其特点是利用多比特位的二进制数据/指令在存储和计算单元中顺序逐条执行,以便完成设定的逻辑计算等功能[1]。目前通用CPU、GPU、TPU 芯片存在致命问题:其一,大数据量的卷积计算造成传统人工智能芯片功耗的激增,不利于人工智能的边缘侧部署,即“功耗墙”问题;其二,由于深层网络包含巨量权值参数,对存储带宽、时延产生更高要求,造成整个系统的计算瓶颈,即“内存墙”问题[2]。
生物大脑的计算方法与冯诺依曼计算体系完全不同,生物神经元利用基于时间/空间编码的尖峰脉冲传递信息,而非二进制编码的数据。脉冲神经网络是一种模拟生物大脑的神经网络类型,使用脉冲序列进行信息传递与运算,这与二进制数计算的传统神经网络完全不同,具有更低的计算资源需求。因此,探索基于脉冲运算的深度学习神经网络体系架构是破解计算瓶颈的新的突破口,具有全新的研究价值。
概率计算是神经网络的重要实现方法之一[3-5],利用离散脉冲序列取代顺序二进制数,实现更低的计算资源占用。然而其在计算时延(latency)或计算精度方面的牺牲也成为硬件设计的挑战。针对上述问题,部分研究者已经进行了一些初步的尝试,Najafi、Sim 等课题组提出了改进概率编码的方法优化上述问题[6-7];Kim 和Liu 等人则采用改进随机数的方法提高其计算效率[8-9];Jenson 等人提出了确定性位流的概率计算方法,可达到更佳的计算精度[10];2020年,Huang 团队基于FinFET 技术,研究了概率逻辑电路的可靠性,为新型纳米器件的应用提供了良好的前景[11]。然而,使用概率计算方法搭建神经网络计算架构仍然是面临的挑战。
基于上述研究成果以及目前仍然存在的各种挑战,本文提出新的设计思想和方案,其主要贡献如下:
(1)基于概率计算规则,对精确概率乘法的时延问题进行优化,并设计了单路/多路概率计算电路;
(2)对比分析了概率计算乘加器与传统布尔逻辑乘加器,并根据实验所得各项物理参数给出结论;
(3)设计了人工神经元与脉冲神经元的统一运算电路,即双神经元形式的计算单元;
(4)搭建了可重构神经网络计算架构,尝试运行多种网络模型,实现毫瓦级的低功耗设计。
本文的组织结构如下:首先,基于概率计算的基础讨论了概率计算乘法与误差来源;其次,设计了低时延、高计算效率的概率计算电路;再次,基于概率计算,将人工神经元向脉冲神经元转换,实现两者运算的统一;另外,基于FPGA 硬件电路设计,验证与实现了概率计算乘加器,并与传统阵列乘加器进行对比分析;再者,搭建可重构的脉冲神经网络计算架构,基于FPGA 设计套件得到资源、功耗数据,并与相关设计进行对比分析;最后,给出文章的结论。
1 概率计算与误差分析
1.1 概率计算基础
基于顺序二进制数的布尔逻辑是计算机处理器和AI 加速器的计算基础,也是传统数字逻辑运算的基础。而概率计算的机制与顺序二进制计算逻辑完全不同,这种离散数字脉冲式的计算方式在加法和乘法计算方面具有独特的优势,具体表现在资源、功耗与吞吐量等方面,在大数据量的并行计算中其优势也将更加明显;此外,其脉冲流形式的数据表现方式更类似于生物神经细胞,而受到了广泛的研究。本文首先阐述概率计算的基本概念和计算机制。
单极性概率脉冲编码(或称为单极性概率计算),其脉冲码流的取值是0 或1,概率脉冲编码通常由输入二进制数、随机数发生器(random number generator,RNG)通过比较器而获得,本文的RNG 采用线性反馈移位寄存器(linear feedback shift register,LFSR)。LFSR 可以产生周期性的伪随机序列,nbit LFSR 生成的随机数的取值范围是0~2n-1,概率脉冲编码电路结构如图1 所示,LFSR 产生的随机数和二进制数输入给比较器,当二进制数大于随机数时输出“1”脉冲,否则输出“0”。
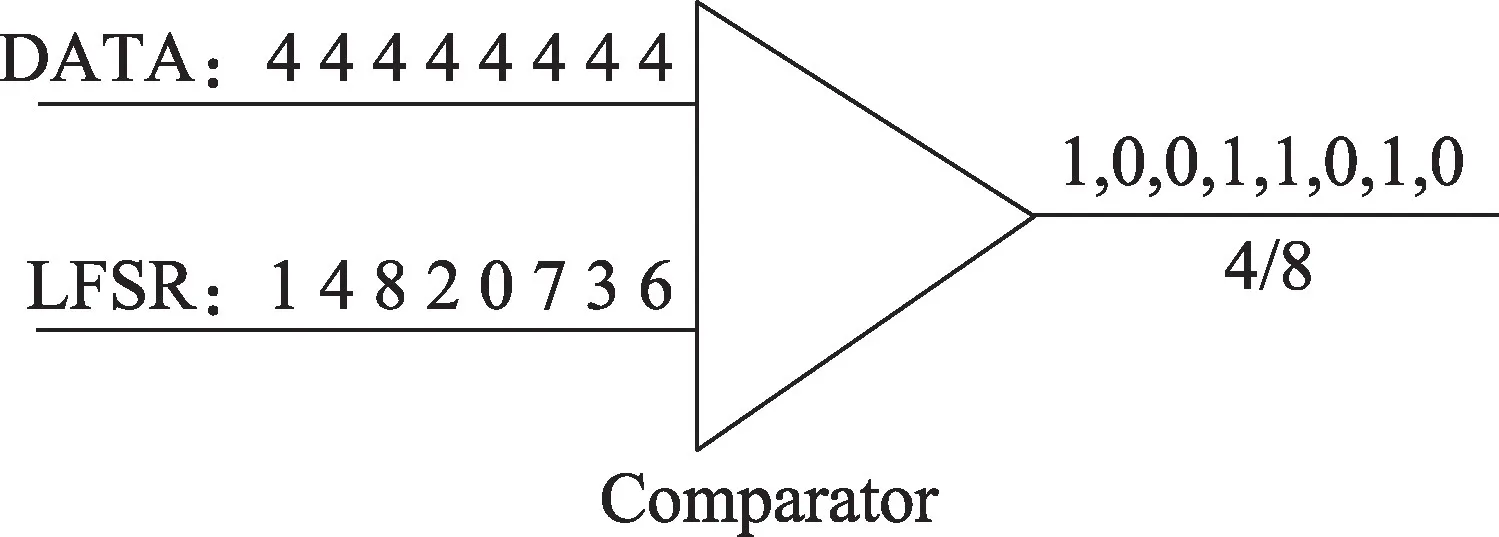
Fig.1 Conversion of binary number into stochastic pulse图1 二进制数向概率脉冲转换的方法
若有两个无符号二进制数Ab(nbit)、Bb(mbit)分别与nbit 和mbit LFSR 比较得到概率脉冲序列As和Bs,那么在序列As和Bs中,出现脉冲“1”的概率分别为:

如果两序列互不相关,则As和Bs同时为“1”的概率P(AB)等于概率P(A)、P(B)乘积,即,当使用概率脉冲表示数值时,乘法运算可以使用一个“与”逻辑门实现:
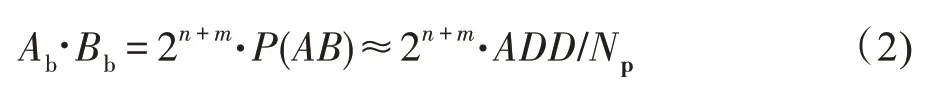
式(2)中用“1”出现的频率代替概率:P(AB)≈ADD/Np,Np是脉冲序列的长度,ADD是乘积脉冲中“1”脉冲的累加数,通常使用计数器进行统计。
假设Np=2L,代入式(2)得:
若L∈N+,那么乘积Ab⋅Bb可由ADD移位n+m-L比特作为近似值,避免从乘积脉冲转换到二进制数值时,产生额外的乘法或除法计算,减少硬件开销。当L=n+m时,可得Ab⋅Bb≈ADD,即“1”脉冲的累加数ADD可直接作为乘积的近似结果,不需要对ADD移位。
1.2 概率计算乘法
如1.1 节所述,在经典概率计算的乘法中,为保证输出脉冲的概率等于两输入脉冲的概率之积,要求两个输入脉冲彼此互不相关,因此不同编码电路中需要使用不同RNG 以产生互不相关的概率脉冲,导致转换器产生较多的硬件资源占用;其次,采用LFSR 作为随机数发生器,并非真随机数发生器,难以保证两脉冲间互不相关,导致在计算中不可避免地产生误差。
假设,Ab(nbit) 为二进制乘数,使用在[0,2n-1]上均匀分布的随机序列Rand与Ab进行比较,脉冲“1”出现的概率为:

设脉冲长度为Np,满足Ab>Rand的随机数个数的期望为:
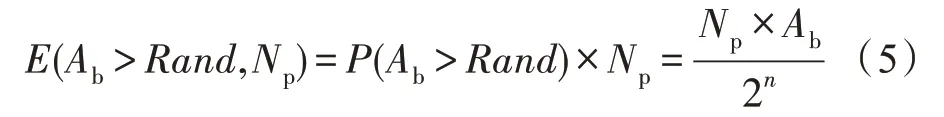
本文采用被乘数调制乘数所产生脉冲串的乘法计算方法[12]。Bb(mbit)为被乘数,对乘数的概率脉冲序列As(长度Np)进行调制,保留有效长度(Nvalid=Np×Bb/2m) 内的“1”脉冲;将舍弃部分的“1”脉冲清零。经过上述调制后的脉冲序列作为Ab、Bb的乘积脉冲,乘积脉冲中“1”的概率将正比于Ab×Bb,如式(6)所示:
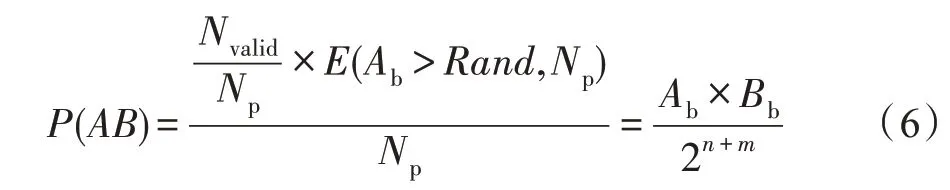
虽然由上述推理可知,乘积脉冲串的概率是正比于二进制数的乘积,但实际计算时,得到的结果往往带有误差,这通常是由以下原因引起的:
(1)样本估计总体导致的误差:由概率转换为乘积二进制数值时,用脉冲“1”的频率代替概率值是一种用样本估计总体的统计思想,频率是试验得到的统计量,概率是计算得到的理论值,随着Np增大,可以使频率在概率附近的波动范围减小,但无法保证频率一定等于概率。
(2)随机数非均匀分布导致的误差:上述推理建立在随机数发生器Rand为均匀分布序列这一条件之上,但实际计算时,使用nbit LFSR 作为随机数发生器,并非真随机数发生器,仅在脉冲长度Np=2n×L且L∈N+时,才具备均匀分布随机序列的特征,式(4)才成立。
(3)计算误差:调制式的概率乘法计算,只有当脉冲串的舍弃部分与有效部分中1 的占比相等时,即Np=2n+m时,乘法结果才准确,否则存在计算误差。
所使用的概率乘法计算,并非对两乘数的概率脉冲进行逻辑与操作实现乘法,而是使用调制式的乘法方式,因此也避免了两乘数的脉冲序列互不相关的制约,可以多个计算单元共用同一个随机数发生器,每个乘数仅需要一个比较器或计数器,有效降低了二进制-概率脉冲转换器的硬件资源开销,且Np=2n+m时可达到与二进制乘法器相同的计算精度[8]。
2 概率计算电路
2.1 脉冲——二进制数转换
1.2 节所提出的概率脉冲调制乘法电路结构如图2 所示,电路包括LFSR、比较器、减法计数器和脉冲序列计数器。2n×Bb作为减法计数器的初始值,每个时钟递减1,当计数到0 后,脉冲计数器的使能信号置零,完成一次乘法运算。
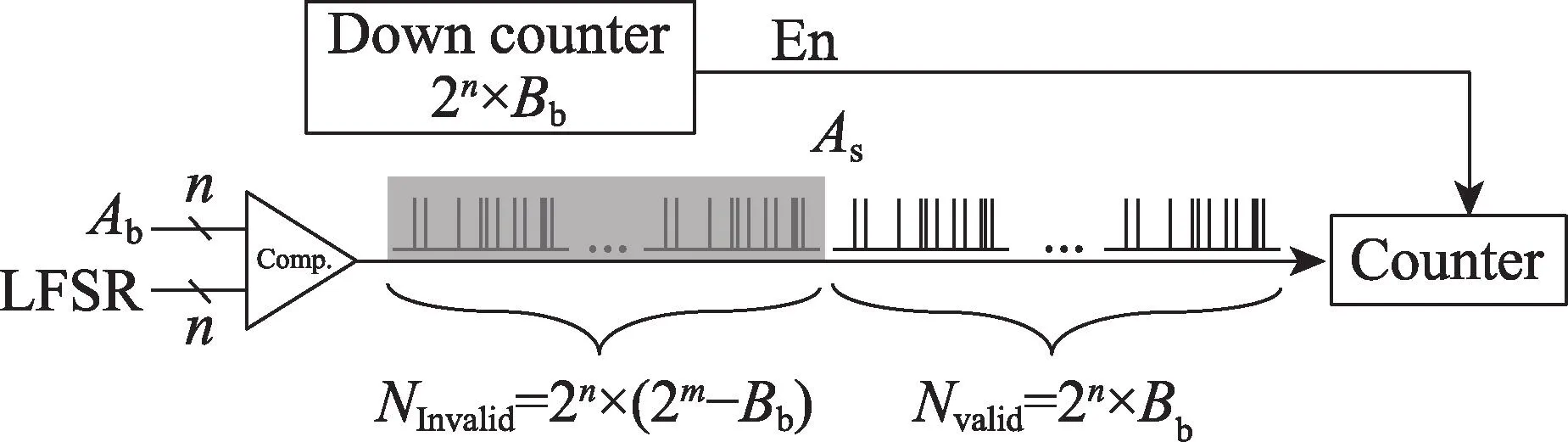
Fig.2 Stochastic multiplication with pulse modulation图2 概率脉冲调制乘法
脉冲长度Np=2n+m是实现精确计算的必要条件,而图2 电路结构需经过Nvalid=2n×Bb个时钟周期才能得到乘积结果,产生较高的时间消耗。为了提高转换效率,本文利用LFSR 产生的随机数序列具有周期性这一特点,实现了多路脉冲的并行发送与并行接收功能。
考虑nbit 的数Ab和mbit 的数Bb进行无符号整数乘法,Ab与nbit LFSR 产生的随机数比较得到概率脉冲序列As,脉冲序列的周期为2n,脉冲长度Np=2n+m;如果将该脉冲按照周期(2n)分组,可分为2m组{As1As2…},各组脉冲序列是完全相同的且长度为2n;若计数器并行接收两组脉冲序列,那么每次接收“1”脉冲的个数只可能为2 或0,因此可将两组脉冲合并为一组脉冲,每接收一个脉冲,计数器执行加2操作;以此类推,若将2L组脉冲序列合并,则每个脉冲会令计数器执行加2L操作。
将合并后的脉冲称作幅度脉冲,长度用Namplitude表示,不同合并数量得到的幅度脉冲,尽管电压幅度相同,但实际包含了不同的累加幅度信息,在实际电路中,通过时间或者空间上的不同进行区分,并且合并前后的脉冲长度有下列关系:Np=2L×Namplitude,2L表示参与合并的脉冲组数。
Np=2n+m的脉冲串进行乘法调制后,有效长度为Nvalid=Np×Bb/2m=2n×Bb,利用上述分组合并的思想,长为Nvalid的脉冲序列可以转换为m组不同合并数量的脉冲序列。例如,Bb为7 bit 且Bb=63 时,有效长度包含63 个周期,基于二进制数按位构造的方式如63=0×26+1×25+1×24+1×23+1×22+1×21+1×20,即(63)10=(0111111)2,其中,Bb二进制形式的第L位为1 时,表示可以从有效脉冲序列中选取2L组进行合并。
为了保证上述计算方式的计算效率,本文设计了新的幅度脉冲乘法器,如图3 所示。乘数Bb的m位分别与Ab的概率脉冲串同时作为m个二输入与门的输入,实现了m组幅度脉冲的并行生成,其幅度值分别对应±20~±2m-1。在脉冲串转换为二进制数的电路中,m组脉冲分别经过m个全加器(FA0,FA1,…,FAm-1)累加构成低mbit 二进制数,而高nbit由计数器累加构成,最终拼接为完整的二进制数存储。
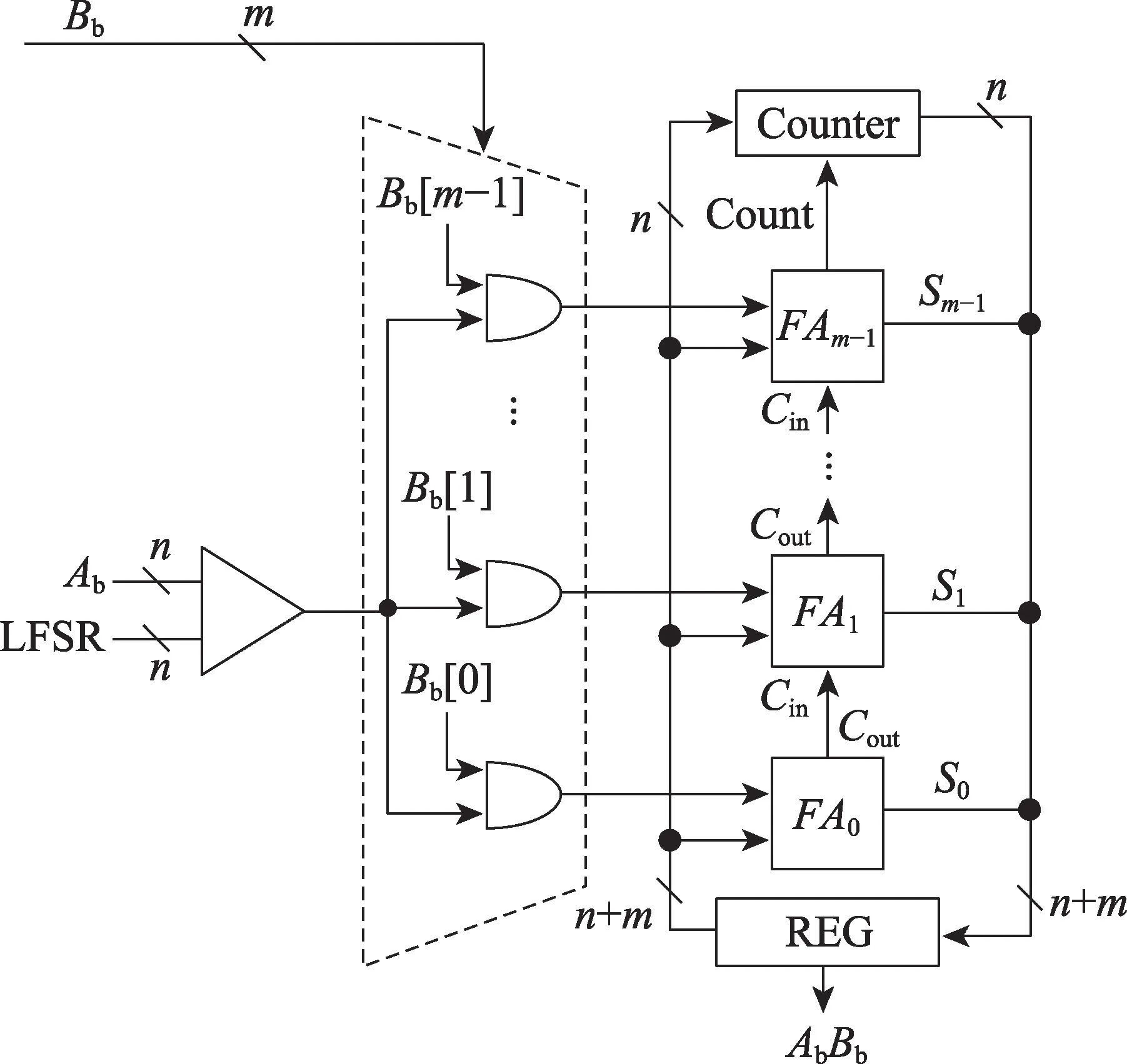
Fig.3 Pulse generator and binary conversion circuit图3 脉冲发生器及二进制转换电路
该方案通过脉冲合并,m组并行发送的方式,大幅度降低了计算时延,由2n+m降至2n个时钟周期,相比图2 方案,仅增加少量硬件资源。使用m组并行的Namplitude=2n带有幅度信息的脉冲代替了串行的Np=2n+m原始概率脉冲,这一方式实质上是对原始的概率脉冲进行了编码转换,并没有改变精确概率乘法需要Np=2n+m的前提条件。
2.2 多路并行概率计算乘加器
在保证计算精度的前提下,如继续改善计算时延,还可将Namplitude=2n的单路m组脉冲串拆分为4路并行m组的脉冲串,则时延可降低为2n-2,其电路结构如图4 所示。
在图3 方案中,nbit LFSR 的作用是产生[0,2n-1]的均匀分布序列,可以用4 个并行的(n-2) bit LFSR代替实现相同功能。(n-2) bit LFSR 产生的数值范围是[0,2n-2-1],将4 个LFSR 的输出数据编号为LFSR1至LFSR4,将随机数送入比较器之前先分别进行下列运算:Rand1=LFSR1,Rand2=LFSR2+2n-2,Rand3=LFSR3+2×2n-2,Rand4=LFSR4+3×2n-2,则Rand1至Rand4的取值范围分别为[0,2n-2-1],[2n-2,2n-1-1],[2n-1,3×2n-2-1],[3×2n-2,2n-1],实现了在[0,2n-1]上均匀分布随机序列的4 路并行输出。基于此方式,4 个(n-2) bit LFSR 与4 个比较器将并行产生4 路脉冲,每路包含m组脉冲序列,可将计算时延缩短为2n-2个时钟周期。
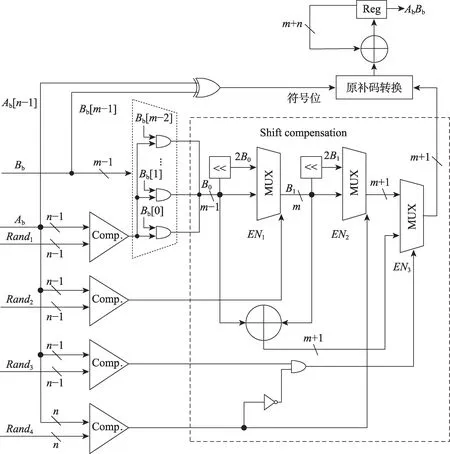
Fig.4 Signed MAC with 4 channels based on stochastic computing图4 带符号数的4 路并行概率计算乘加器
图4 的4 路并行脉冲发送具有如下特点:4 路脉冲均使用同一个Bb作为脉冲的调制乘数,对于二进制转换电路而言,即任意一路如果发送了“1”脉冲,对应的累加值均等于Bb,否则为0;Rand1至Rand4的取值范围依次增大,当第L路发送“1”脉冲时,第L路以下的也一定发送脉冲“1”,因此仅使用m个与门对Rand1产生的概率脉冲进行调制,其余3 路发送“1”脉冲时,可根据第一路m组脉冲确定累加值;在一个时钟周期内,每有1 路发送了脉冲“1”,加法器就需要累加1 次Bb,即一个时钟周期内,Bb的累加次数等于发送了脉冲“1”的通路数。
二进制转换电路设置移位补偿模块,其目的是将4 路脉冲通路在每个时钟周期里产生的4 次累加运算,并行地在一个时钟周期内完成。由于上述脉冲“1”的特殊发送规律,显著简化了移位步长模块的电路结构,相比于图3 方案,虽然该方案硬件资源增加约78%,但计算速度是原先的4 倍,因此,综合计算效率比单通道又提高约1.25 倍。
由于实际计算往往是有符号数的乘累加运算,图4所示电路还包含原-补码转换模块。对于Ab(nbit)、Bb(mbit)的有符号数运算,Bb、Ab以原码形式表示,最高位各有1 bit 符号位,累加值需要先进行原补码转换,再完成累加,乘加运算结果为补码形式。
3 神经网络计算架构
3.1 神经元基础
无论是传统的人工神经网络还是卷积神经网络都是参考神经元结构和功能实现的数学模型,并以人工神经元作为网络的基本单元,其基本逻辑功能如图5 所示,X=[x1,x2,…,xi]是神经元的输入信号,W=[w1,w2,…,wi]是与神经元相对应的权值,i是表示神经元个数的正整数,每个神经元对输入和权值进行加权求和得到膜电位。
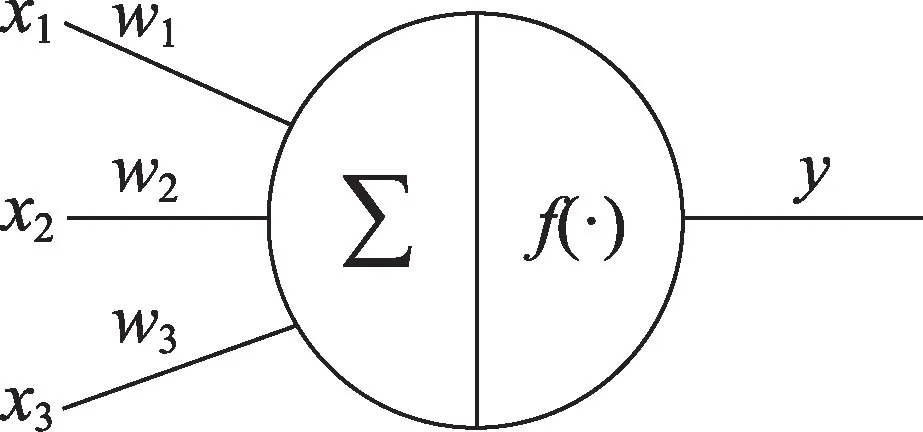
Fig.5 Neuron model图5 神经元模型

而神经元本身都存在偏置信号θ,在外界激励的作用下,其结果经过激活函数f后输出,其完整表达如下:
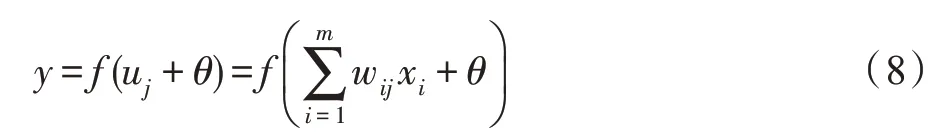
不同于传统人工神经元,脉冲神经元则模拟了生物神经元的运行特点。神经元接收脉冲信号P(t)=[p1(t),p2(t),…,pm(t)],根据连接权值增强或抑制膜电位;神经元达到阈值电压时会进入激活状态,向下一层神经元释放脉冲并将膜电位快速拉低至静息电位,也就是进入不应期。所对应神经元膜电位表达式:
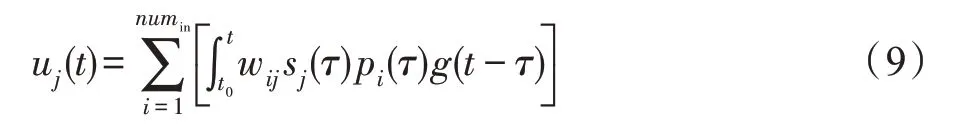
式中,u、p、s、w分别为膜电位、神经脉冲、激活状态(未激活时s=1)和权值,g(t)为一个尖峰脉冲对膜电位所产生增量随时间t的变化曲线。
为了以数字电路的形式实现运算,需对时间域离散的脉冲神经元重新建模,将尖峰脉冲替换为方波,设T为采样间隔,则可以得到下述表达式:

将每两个采样点之间的时间段划分为一个活动周期,同一个活动周期内的神经元活动(收发脉冲)视为同时进行的,因此式(9)的计算需要记录从上一个不应期结束时刻(n0T)到当前时刻的所有活动周期的输入脉冲数据,计算量庞大,计算效率低,于是对膜电位变化曲线g(t)进行改进,采用如图6 的分段拟合方法实现,即g(nT)=2-nT,用tn表示nT,且T=1,则式(10)可以简化为式(11):

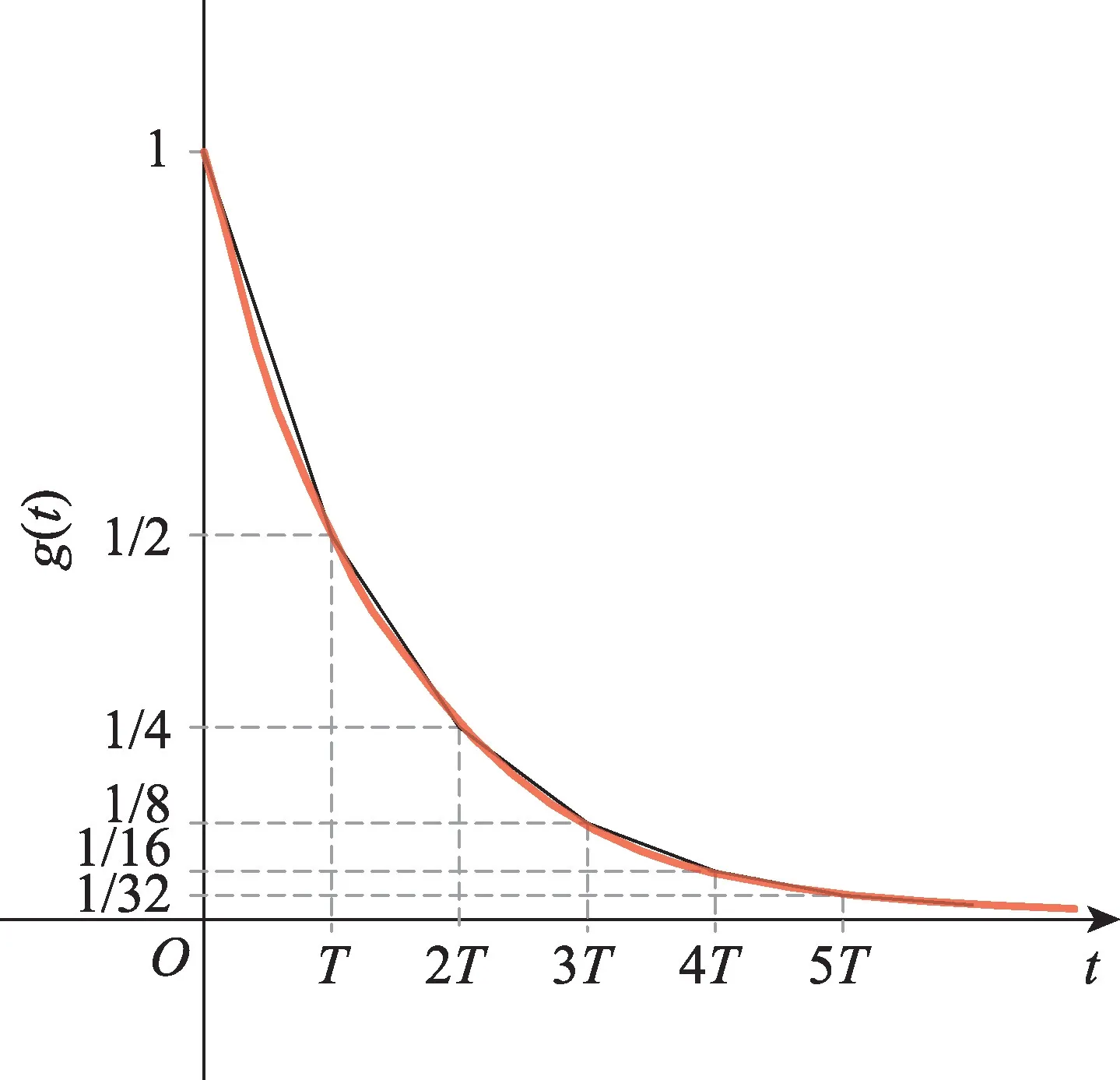
Fig.6 Piecewise fitting membrane potential curve图6 分段拟合的膜电位变化曲线
根据上式,神经元在当前活动周期结束时的膜电位可由上一活动周期结束时的膜电位uj(tn-1)、当前活动周期的接收脉冲pi(tn)以及自身状态sj(tn)求得,避免了大量的运算,且g(t)变化曲线系数取为1/2,也即上一活动周期膜电位的衰减系数,通过移位实现,进一步减小硬件资源开销。
基于脉冲神经元膜电位表达式构造脉冲神经元模型,如图7 所示。神经元电路结构包含:脉冲接收器、实现膜电位衰减的移位器、判断激活条件的比较器、脉冲发生器等。

Fig.7 Spiking neuron circuit图7 脉冲神经元电路结构
3.2 双神经元计算单元
基于概率计算范式,可将人工神经元转换为脉冲神经元完成对应运算。为了实现片上神经网络重构系统,本文提出了双神经元结构作为基本计算单元(processing element,PE),模拟输入神经元到输出神经元的概率脉冲传输过程。输入神经元包括本地权值存储单元、膜电位及其激活单元和概率脉冲调制乘法单元(包括比较器和LFSR 等);输出神经元包括脉冲接收模块、膜电位移位寄存器。
对于单个神经元结构而言,其工作过程为:输入数据经过乘法、加法再经过激活函数,并根据权值发送脉冲编码信号。而在双神经元结构中,输入数据位于输入神经元,先经过激活函数,再根据权重发送脉冲;输出神经元将接收到的脉冲累加至膜电位寄存器,并在切换活动周期时衰减膜电位。
基于上述概率计算的双神经元,本文提出了基于概率计算的脉冲神经元与传统神经元可重构的设计方案。针对神经元的乘加运算(式(7))以及脉冲神经元的条件加权的累加运算(式(11)),均采用概率脉冲编码的方式转换为脉冲形式实现运算,以实现在同一个电路架构下,同时支持不同神经元模型的计算功能:

式中,Cij(m)为基于概率计算得到的频率编码脉冲序列,对于脉冲神经元的计算具有如下转换关系,α与Cij的编码长度N相关。

对于传统神经元的计算具有如下转换关系,α同样与脉冲编码长度N相关,且进行人工神经元计算时,式(12)中上一活动周期膜电位衰减uj(tn-1)/2 用偏置θ代替,sj、pi取值为1。
另外,由于卷积计算具有规则性和重复性,输入特征图的不同像素点将与同一个权重数值进行乘法运算,即卷积计算的重要特点之一“权值共享”,如果将权值作为乘数的概率脉冲信号,膜电位激活值作为被乘数,也就是概率脉冲调制的使能信号,那么可以将多个计算单元的比较电路进行合并,如图8 所示,共用一个权重数值,并行进行多个乘加运算,比较器电路的资源平摊到各个计算单元中,每个计算单元的平均开销就能够进一步降低。
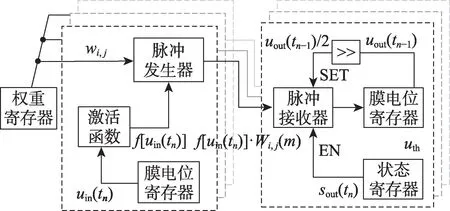
Fig.8 Double neuron computational unit with shared weight图8 权值共享的双神经元计算单元
3.3 神经网络的可重构架构
基于双神经元计算单元设计了可重构神经网络运算架构,用xm-ym,k符号表示一个双神经元计算单元,其中xm代表脉冲发生电路,连线代表权重,ym,k代表接收器且采用图4 所示电路结构。
基于双神经元概率计算的神经网络计算架构如图9 所示。其中,输入膜电位ui,m(tn)存入xm,判断激活情况并根据权重大小向ym,k发送概率脉冲;tn-1活动周期膜电位uo,k(tn-1)衰减1/2 后从输入端输入,并依次经过y1,k,y2,k,…,ym,k,接收各输入神经元发送的脉冲信号,完成一系列累加运算,从输出端输出tn活动周期的膜电位数值uo,k(tn)。
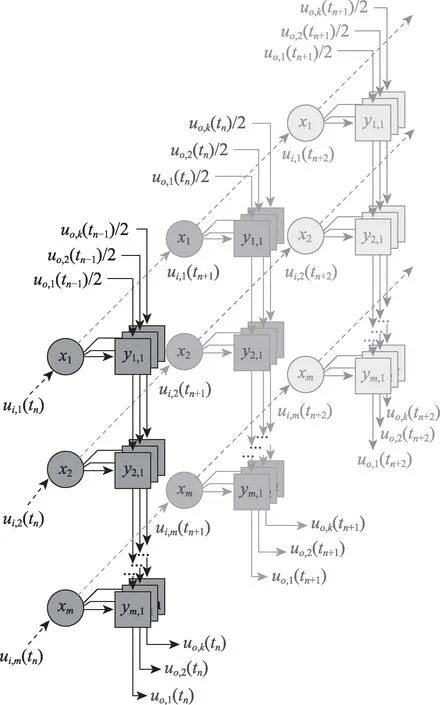
Fig.9 Computing array based on double neuron图9 双神经元计算阵列
上述运算过程为脉冲神经网络的一层运算,输出的膜电位数值既被用于当前层的下一活动周期运算,同时也是网络下一层的输入神经元膜电位,参与下一层当前活动周期的运算。当网络的所有层依次完成运算后,则一个活动周期计算完毕,进入下一个活动周期,并再次重复上述过程。
为了适配SNN(spiking neural network)和CNN(convolutional neural network)网络可重构结构,设计了控制与数据路由模块,用于计算阵列的配置与复用,实现对计算资源的充分利用;一个阵列的尺寸设置为m=3,k=32,共96 个双神经元单元。两者组成一个可以独立完成网络处理工作的计算核,可实现多种模态的神经网络运算。
4 硬件实现
4.1 乘累加单元性能对比
为了验证概率计算构造的逻辑电路性能,概率计算乘加器与经典的二进制数阵列乘加器进行了对比。使用包含相同16 个计算单元构造的乘加器计算电路,从而并行执行乘累加运算。乘累加运算uj=,其中,i=1,2,…,16。
本实验使用的FPGA 芯片是KINTEX-7,二进制乘加器受限于关键路径,插入一级流水后最高时钟仅达200 MHz,而概率计算方法最高时钟频率可达700 MHz,即所采用FPGA 芯片的时钟上限。因此,本实验对概率计算给出两套时钟频率的实验结果,均基于FPGA 配套的设计套件得到硬件实现的各项报告,整理如表1 所示。
以OPS 为单位的能效数值存在一个取值范围,与不同Tc取值一一对应,例如单路方案700 MHz 能效换算为:最高能效时Tc=1,243.5 GSOPS/W=487 GOPS/W;最高精度时Tc=128,243.5 GSOPS/W=3.8 GOPS/W。同理4 路方案700 MHz 能效换算为:最高能效时Tc=1,722.6 GSOPS/W=361.3 GOPS/W;最高精度时Tc=32,722.6 GSOPS/W=11.3 GOPS/W。
表1 中统计对象是16 个计算单元并行时的资源开销,功耗是在同等条件下完成对数据输入输出获得的结果。不同的乘法器电路对功耗的影响,也即计算逻辑电路产生的功耗,在FPGA 中主要体现在clocks、signal、logic 上,因此表1 列出的功耗仅为三者之和的动态功耗。其余功耗如时钟管理器(MMCM)功耗和静态功耗主要由FPGA 本身以及I/O 决定,与所设计的计算逻辑电路无关。

Tabel 1 Performance comparison between traditional MAC and stochastic MAC表1 二进制阵列乘加器与概率计算乘加器性能对比
由于使用概率计算实现乘累加运算时,计算时长与计算精度有关,难以直接用乘加操作作为衡量算力计量单位,引入另一种算力计量单位:概率计算中的计算操作称作突触操作(synaptic operations),是一种条件加权的累加操作,最早由IBM 的True-North团队提出[2],对应的算力单位为SOPS,表示每秒进行的累加操作次数。
4.2 神经网络实现
在KINTEX-7 上实例化了16 个3.3 节所述计算核并行运行,时钟频率设置为350 MHz,基于FPGA配套设计套件得到各项报告,如图10、图11 所示,并完成了如下几个常见SNN 或CNN 模型的运行实验,各网络模型的权重数据均采用8 bit 量化方案,且Tc设置为32,即精确乘加计算。
基于综合报告,计算每个核的峰值算力为134.4 GSOPS;与表1 相同,功耗部分不计入与逻辑电路无关的时钟管理模块功耗、静态功耗与I/O 功耗,平均单计算核功耗为227 mW,峰值能效为0.592 TSOPS/W。

Fig.10 FPGA synthesis report of single core(350 MHz)图10 计算核FPGA 综合报告(350 MHz)

Fig.11 FPGA synthesis report of 16 cores(350 MHz)图11 16 核FPGA 综合报告(350 MHz)
4.2.1 SNN 神经网络实现
基于单层SNN 的监督学习算法,对网络进行训练,使用MNIST 数据集,网络结构为一层全连接形式的SNN 网络,输入神经元784 个,输出神经元10 个,对应手写数字0~9,共10 个类别。
训练所得网络测试集正确率为89.3%,8 bit 量化后正确率为89%,降低0.3 个百分点。由于MNIST 的图像数据为二进制数值,在进行SNN 运算前还需要将图像编码为脉冲序列。利用概率脉冲编码,将28×28 个像素点的二进制灰度值转换为784个输入神经元(784=28×28)各自发送的Np=256 脉冲序列,也即256 个活动周期。
双神经元PE 的计算顺序为:输入神经元膜电位,经过激活函数后产生脉冲;输出神经元接收脉冲,进行累加运算得到输出膜电位。而单层SNN 计算顺序为先进行累加运算得到输出膜电位,再经过阶跃形式的激活函数(阈值比较)得到输出神经元发送的脉冲,并根据产生脉冲的先后或者有无,判断分类结果。因此阵列计算时需要设置为两层以实现上述运算。第一层负责膜电位计算的累加与衰减操作,第二层则仅负责激活判断,不进行计算操作。
搭建了相应的显示系统,如图12 所示,第1、3 行为随机选取的数据集图像,第2、4 行为相应的识别结果。

Fig.12 MNIST dataset and SNN operation mode图12 MNIST 数据集与SNN 运行模式
4.2.2 Stochastic CNN 神经网络实现
根据3.2 节的基于概率计算的神经元转换方法,对两种常见CNN 模型进行SNN 转换,转换后的网络模型既不完全与SNN 一致,也不同于CNN,称其为SCNN(stochastic CNN),SCNN 的计算结果与Tc存在较大关系,采用4 路方案的概率计算时,当Tc=32时,网络运行结果与原CNN 一致;Tc<32 时,计算与原CNN 模型相比将产生误差,实验中使用Tc=32 的精确计算模式。
使用前述计算核进行硬件加速,各CNN 模型同样采用8 bit 量化:首先,通过计算机软件仿真对转换后网络模型的准确率进行了测试,由于采用Tc=32的精确计算模式,因此转换前后的计算结果是一致的,准确率并没有损失;其次,对电路进行功能仿真,得到详细的电路运算过程,并观察运行结果(膜电位变化以及神经元激活情况等)与软件仿真结果完全一致,同时根据仿真时间得到各模型的处理帧率,各项实验结果如表2 所示。

Table 2 Performance of common deep learning networks with single core表2 常见深度学习网络的单核性能
在传统的二进制计算过程中,受到数据调度与计算时间不均衡的限制,无法时刻处于峰值计算状态,PE 利用率一般很低,如表3 所示,列出了几款现有硬件加速器所能达到的PE 利用率。

Tabel 3 Comparison of PE utilization rate表3 PE 利用率比较
列举的三款加速器采用ASIC 实现,算力与能效的计量单位也非突触操作,因此均值能效、峰值能效与本设计并不具有可比性,但PE 利用率与电路实现方式无关,而与所采用的计算架构有关,因此是有对比意义的一项属性。本文基于概率计算以脉冲神经元的形式完成运算操作,对数据读写速度的需求大幅降低,更易实现数据调度与脉冲计算的同步进行,保证了计算时间与调度时间的均衡,大幅度减少了计算单元等待数据调度的空闲时间,因此达到了极高的PE 利用率。
5 结论
神经网络基础计算单元直接影响其硬件加速器的计算能效。本文提出了基于低功耗、高计算效率的概率计算的基础单元——乘加器。基于概率计算单元构造了脉冲神经网络和概率卷积神经网络,并实现了支持SNN 与SCNN 运算的可重构计算核心:北航筹算(BUAA-ChouSuan)。
基于KINTEX-7 平台对几种乘加器方案进行对比测试,相比于经典的二进制乘加器,概率计算模式的乘加器单元在面积与功耗方面具有明显的优势。在200 MHz 时钟频率下,单路概率计算的逻辑资源开销(LUT)降低80%,功耗降低76%,最高能效比是二进制乘累加器的8.82 倍。在SCNN 网络计算中,测试了LeNet 与AlexNet,在时钟频率350 MHz,均值能效可达0.536 TSOPS/W,PE 利用率在90%以上。对MNIST 数据集,在8 bit 量化权重,Tc=32 条件下,识别精度可达97.87%与98.28%。
