下肢外骨骼膝关节模糊滑模位置控制器设计

李鹏杰 王新蕊 李小奇 许国强 司访 张煜 叶冬雨

（中国兵器工业第二〇八所，北京，102202）

引言

下肢助力型外骨骼系统是一种穿戴于人体的助力装置，目前主要运用于单兵，以提高士兵的物资搬运携行及快速机动能力.为贴合实战提高穿戴舒适性，下肢助力外骨骼膝关节需具有贴合人体、结构简单等特点，无法安装力矩传感器，因此大多采用位置环控制.在人机系统行走步态周期内，外骨骼膝关节面临负载冲击大、变化范围广等困难，一般控制算法难以达到理想的控制效果.滑模控制是一种变结构控制，拥有随时开关的特点，可以进行设计且对象与扰动无关，响应速度快、对参数变化及扰动不灵敏、物理实现简单，从而为复杂机电系统控制提供了一种较好的解决方案.但是当系统阶数较大或者结构参数不确定时，很难直接获取控制率，同时抖振问题一直制约着滑模控制的工程化运用.针对上述问题，国内外专家学者提出了很多解决方案，主要有趋近率法、边界层法、观测器法和与智能算法结合等.胡飞等[1]设计了一种模糊PID滑模控制系统，有效解决了下肢外骨骼步态控制过程中电液伺服系统存在的非线性、外在干扰等问题.宋胜利等[2]提出一种快速二阶终端滑模控制策略，将绝对值函数隐藏在积分项里，提高了传统二阶终端滑模控制的全局收敛性.熊少峰等[3]提出一种非奇异终端滑模方法，有效克服了奇异问题.Utkin V I等[4]在控制率中引入等效控制来预估外界干扰.Elmokadem T等[5]基于super twisting算法设计的二阶滑模观测器能够快速稳定估计出外界干扰，从而削弱抖振.上述研究大多采用传统趋近率和滑模面，很难实现系统快速性和稳定性的统一.

本文针对下肢助力外骨骼膝关节，设计了一种自适应滑模位置控制器，采用单输入双输出的结构形态，被控对象的输入量应用快速终端趋近率求取，选择滑模函数S作为模糊控制器的输入项，分别选择幂级趋近项系数k1和指数趋近项系数k2作为模糊控制器的两个输出项，依据系统运动动态特性与两个输出项之间的关系，制定模糊规则，使得系统状态点远离滑模面时，趋近率大，离滑模面近时，趋近率小，保证系统最大程度抑制抖振的同时快速趋近滑模面.

1 下肢助力外骨骼膝关节结构及数学模型

1.1 膝关节结构及永磁同步电机数学模型

图1给出了下肢助力外骨骼膝关节结构图，系统主要由永磁同步电机、减速器、编码器、驱动器等部件组成.为提高控制精度，系统采用三闭环控制，其中电流环和速度环采用数字控制，位置环的反馈值取执行机构轴端编码器值.

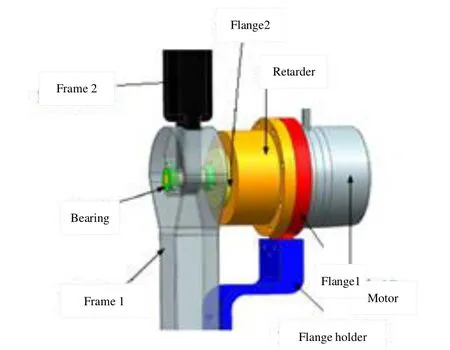
图1 膝关节系统结构图Fig.1 An illustration of knee joint system

在不影响控制性能的情况下，假设：涡流和磁滞损耗几乎为零，电机铁芯饱和忽略不计，电机气隙磁场皆均匀分布，三相绕组的感应电流均以正弦波形式作用.依据假设的情况，采用id=0的控制策略实现对转矩控制的线性化和解耦控制.基于旋转坐标轴（dq轴坐标系），可以得出系统线性状态方程[6-8]：

式中，L为等效dq轴产生的电感；iq为q轴上的电流；TL为折算到电机轴上的总负载转矩；R为定子相电阻；ωr为转子的机械角速度；B为黏滞摩擦系数；ψf为转子上的磁势；Te为电机轴输出转矩；J为折算到电机轴上的总转动惯量；Pn为极对个数.

1.2 膝关节伺服系统状态空间模型

膝关节伺服系统采用三闭环控制，其中位置环选用模糊滑模控制器，速度环简化为PI控制，电流环简化为P控制.由于模糊滑模控制对系统参数精度要求低，故将机械部分假设成刚性体，电气部分处于理想状态，可得速度环的传递函数为[9]：

式中，τm=L/R是速度环时间常数，K是速度环增益.将减速器考虑成积分环节1/(is)，i为减速比，可得膝关节伺服系统开环传递函数为[10]：

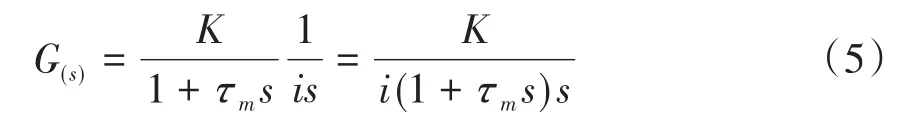
可得下肢助力外骨骼膝关节伺服系统结构图如图2所示.其中，θ为实际位置并作为反馈量，θref为指令位置，位置控制器的输出量ωref是被控对象的输入量，设u=ωref，系统的状态向量为X=[x1x2]，其中x1=θ，x2=θ̇，则系统状态空间方程为[11-13]：

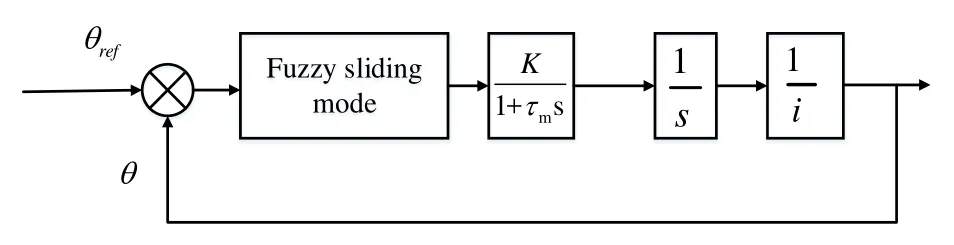
图2 下肢助力外骨骼膝关节位置伺服系统结构简图Fig.2 Structure diagram of knee joint position servo system of lower limb assist exoskeleton

式中，f(x)=-1/τmx2；g(x)=K/iτm考虑系统经常受到不确定因素的影响，为提高状态空间方程精度，需增加不确定项：

式中Δf，Δg为添加的不确定部分，假使系统满足条件

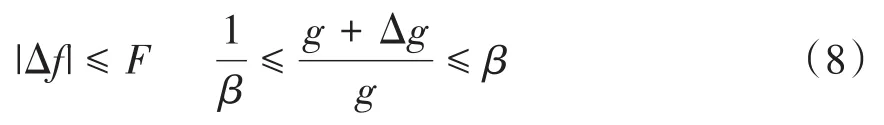
式中，β≥1且为常数，F为标量值.

2 模糊自适应滑模控制器设计

2.1 滑模控制器设计

2.2 趋近率系数与滑模运动特性关系分析

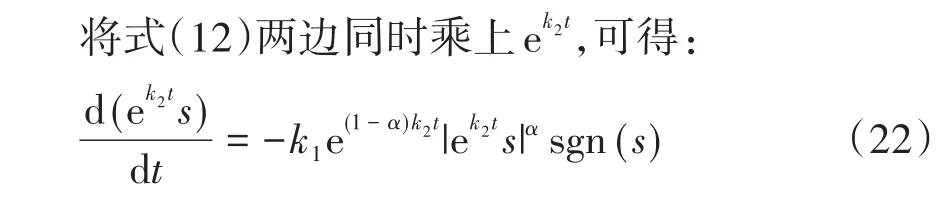
可知式（12）中的“-k2s”项具有加速收敛的作用.结合传统幂次趋近率特性，可知当远离滑模面时，k1，k2均应取较大值；当接近切换面时，为抑制抖振，k1，k2应取相对较小值，整个过程中应保证k11.

2.3 模糊自适应滑模控制器设计

根据上述趋近率系数与滑模运动特性关系，将模糊控制器设计成单输入双输出结构形式.即：运用模糊规则，根据滑模函数s的值，自适应调整k1和k2的值.将s的值归一化到区间[-1，1]上，并将s分为正大、正中、正小、几为零、负小、负中、负大等7种情况，模糊子集为｛NB，NM，NS，ZO，PS，PM，PB｝；将系数k1和k2的值归一化到区间[0，1]上，分为几为零、正小、正中、正大等4种情况，模糊子集为｛ZO，PS，PM，PB｝；隶属度函数均选用三角函数.根据上述滑模动态特性与趋近率系数之间的关系分析结果，制定14条模糊规则，如表1所示.

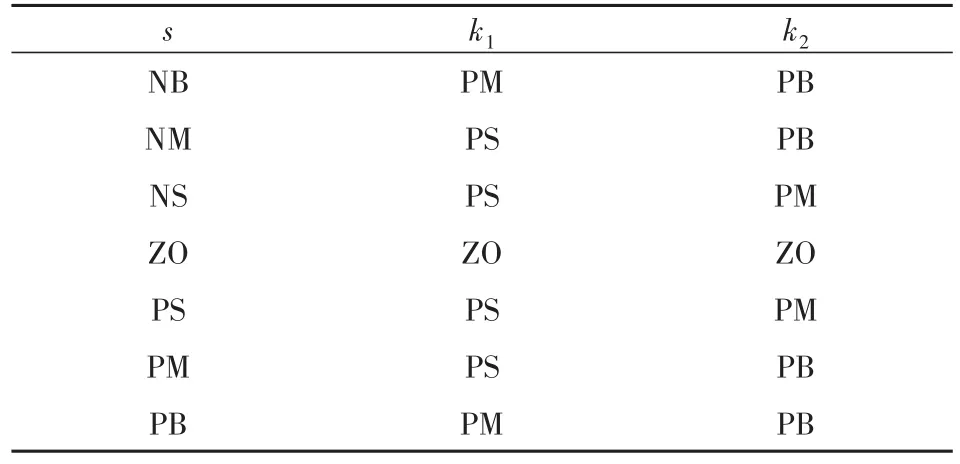
表1 模糊控制器规则表Table 1 Rule table of fuzzy controller

采用重心法解模糊，可得：

则被控对象的输入为

膝关节模糊自适应滑模控制系统机理如图3所示.

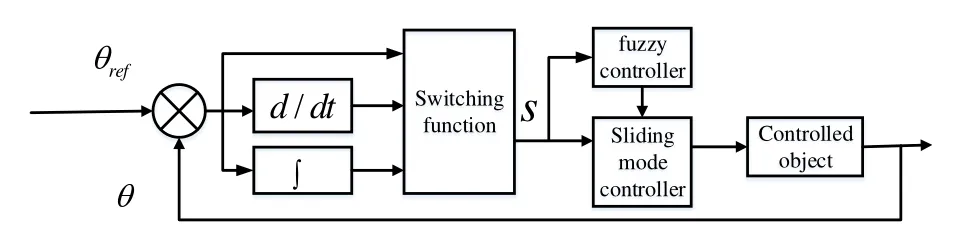
图3 模糊自适应滑模控制器控制机理图Fig.3 Control mechanism of fuzzy adaptive sliding mode controller

3 仿真结果及分析

为验证控制策略的正确性，运用Matlab/Simulink进行仿真实验，并与经典PID和经典模糊自适应滑模控制策略（即：滑模面选取s=e+cė，其中c为常数，趋近率选取指数趋近率）相比较.仿真模型具体参数如下：模糊滑模控制器参数为c=126，m=11，k3=15，k4=1200；电机转子惯量J=2.627g⋅m2，等效电感L=50mL，永磁体Ψf=0.056Wb，电机磁极对数Pn=4，相间电阻R=1.38Ω，额定电流Ic=21A，摩擦黏滞系数B=1.26 × 10-4N·m·s；谐波减速器减速比1∶120，速度增益K=120，电流环参数为[P，I，D]=[0.715，0，0]，速度环参数为[P，I，D]=[5.2 × 10-5，0.2884，0]，位置环参数为[P，I，D]=[10000，0，0].仿真时间设置为2s，求解器选择ode45.

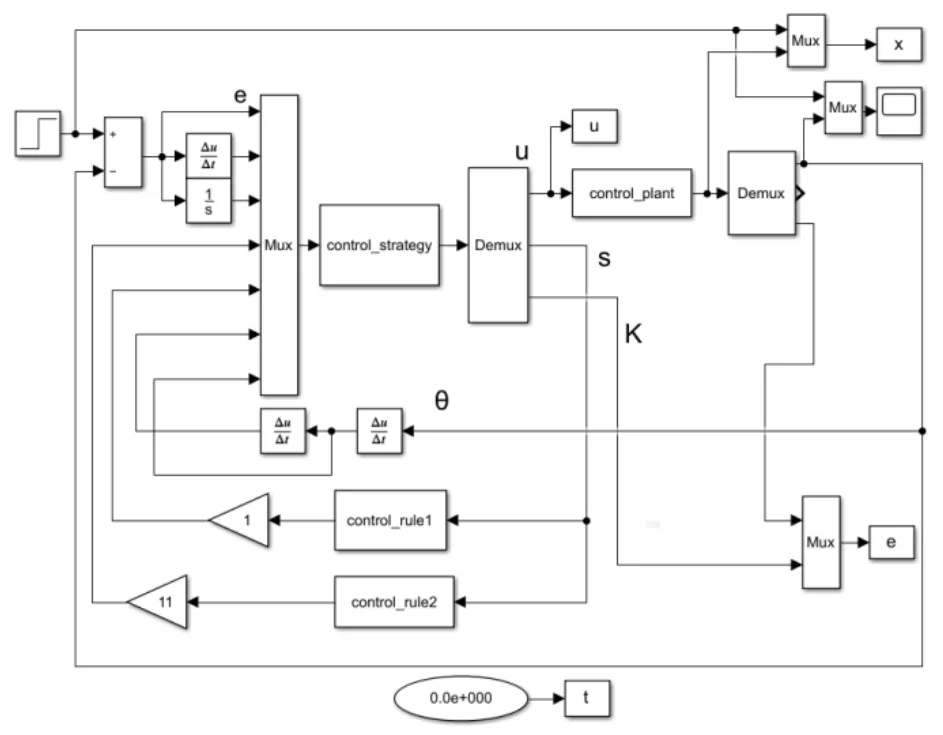
图4 新型滑模控制策略仿真模型Fig.4 Simulation model of new sliding mode control strategy

3.1 常值负载干扰

为验证下肢助力外骨骼膝关节位置控制器抗干扰能力，在1s时突加一个值为10N·m的阶跃信号，如图5所示，经典PID和滑模控制器出现很大位置偏移，很长时间才恢复到平衡位置，且初始位置响应较慢；新型滑模控制器系统基本不受影响，且初始位置响应较快.

图5 阶跃响应曲线Fig.5 Step response curve

3.2 位置跟踪误差

为验证控制系统的跟踪性能，选取r=20sin(1.24t)做为系统的跟踪曲线，如图6所示，新型滑模控制器的跟踪误差远小于经典滑模、PID控制器的跟踪误差.

图6 跟踪误差曲线Fig.6 Tracking error curve

4 实验验证

实验系统选用STM32F407ZGT6作为位置控制核心板，电机选用J56ZWX02无刷直流电机，额定转速3058r/min～3258r/min，额定扭矩1.5N·m，谐波减速器减速比1∶120，电流环为P控制，采样频率20kHz，速度环为PI控制，执行频率10kHz，位置环依次选用经典PID控制器、经典滑模和新型滑模控制器，执行频率1kHz.系统输入选用正弦信号r=20sin(1.24t)，修正参数如下：c=126，m=11，k3=15，k4=1200.角度初值为0.08，自变量s的量化因子为0.3，变量s和ṡ的输出量化因子为6.3×10-7和3×10-7.实验结果如图7所示，与经典滑模和PID控制策略相比，新型滑模控制策略的毛刺和误差峰值明显减小.

图7 实验控制跟踪误差对比Fig.7 Comparison of tracking error with experimental control

5 结论

针对下肢助力外骨骼膝关节位置伺服系统，设计了一种模糊自适应滑模控制策略.仿真及实验结果均表明，该控制策略与经典滑模、PID控制策略相比，跟踪误差更小、响应速度更快、鲁棒性更强，该控制策略完全能够满足下肢助力外骨骼膝关节位置环主从伺服跟踪工作要求.