基于A-FFRLS算法的永磁同步电机转动惯量辨识研究

田 威，张幽彤，李建航

(北京理工大学 清洁车辆实验室，北京 100081)

0 引 言

永磁同步电机(以下简称PMSM)广泛应用在高精度、高性能的工业场合，这对其速度动态性能提出了更高的要求。电机在运行过程中转动惯量是恒定的，进行离线辨识即可，然而对于整个电机系统，在不同负载工况下，作用在电机轴上的力发生改变，使电机系统的转动惯量发生变化，进而导致系统的速度响应特性降低，最终影响整个系统的机械特性[1]。在工业场合的实际应用中，PMSM的转动惯量要小于异步电机，对外部环境或者工况变化更加敏感，其调速系统受负载惯量的影响更大[2]。因此，准确辨识PMSM系统的转动惯量值，对提升调速系统的动态性能意义重大[3]。

针对PMSM转动惯量准确辨识问题，国内外学者进行了大量研究。PMSM转动惯量辨识方法主要有离线辨识和在线辨识[4]。离线辨识[5-6]是在电机工作前完成对电机参数的测量，其易于实现但是不能实时获得电机运转中惯量参数的变化，不适用于对精度与动态性能要求高的工业场合。在线辨识方法[7-8]可以在电机系统运行过程中，实时获取电机的参数来完成惯量参数辨识，其辨识方法主要有卡尔曼滤波法(EKF)、递推最小二乘法(RLS)、模型参考自适应法(MRAS)等[9]。文献[10]使用EKF算法，将惯量值作为状态变量，通过滤波算法对其进行辨识，其所需数据量较大和计算复杂等问题有待解决；文献[11]提出利用遗忘因子递推最小二乘法(以下简称FFRLS)来完成转动惯量的辨识，仿真结果具有较快的收敛速度和辨识精度，但是其遗忘因子值固定，无法保证辨识效果最优；文献[12]采用基于模型参考的自适应辨识，其辨识精度较高，然而模型中的自适应率需要不断更换，不具有通用性；文献[13-14]分别提出了重力搜索算法(GSA)和变步长Adaline 神经网络算法，这些智能算法虽然对于参数辨识具有较高精度，但是其实现复杂，需要大量的迭代计算或训练，计算耗时长，无法满足系统的快速响应要求。

针对以上转动惯量辨识算法存在的问题以及对算法复杂度和实用性的综合考虑，本文设计了一种自适应遗忘因子递推最小二乘算法(以下简称A-FFRLS)的转动惯量辨识方法，在FFRLS算法基础上，引入模糊控制理论[15]对遗忘因子值进行动态控制，使惯量辨识系统可以根据算法辨识结果与实际值之间的差距自适应调整遗忘因子值，使惯量估计值能够快速且准确地逼近真实值，从而实现转动惯量的实时在线辨识。本文通过仿真和实验，对比了A-FFRLS与FFRLS算法对转动惯量的辨识结果，证明了所设计的算法在对PMSM进行转动惯量辨识时，在保证辨识速度的同时，具有更高的稳定性和精度，可为电机的调速控制提供参数依据。

1 转动惯量辨识策略设计

1.1 基于遗忘因子的递推最小二乘算法

常规的最小二乘算法收敛速度慢，因此为提高收敛速度，需要引入遗忘因子进行数据加权[16]，其算法基本步骤如下。

PMSM系统模型定为自回归模型：

y(k)=φT(k)θ+ξ(k)

(1)

式中:k表示时刻；y(k)为k时刻系统输出;φT(k)为测量数据向量;θ为实际的参数向量；ξ(k)为噪声向量。

(2)

加入遗忘因子λ(0<λ<1)，系统的目标函数：

(3)

(4)

1.2 PMSM转动惯量辨识

PMSM机械转矩平衡方程：

(5)

式中:Te与Tl分别为电机的驱动转矩和负载转矩；J为转动惯量；ωm为机械角速度；B为阻尼常量。

对式(5)进行Laplace变换,以ωm为输入，以Te-Tl为输出，系统的传递函数：

(6)

通过式(6)可推导出系统带零阶保持器的脉冲传递函数：

(7)

式中:Ts为相邻两个采样周期间隔。联立式(5)和式(7)，将电机的机械转矩平衡方程离散化，可得：

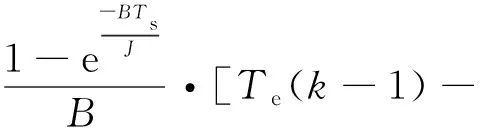
(8)

进一步整理可得：

(9)

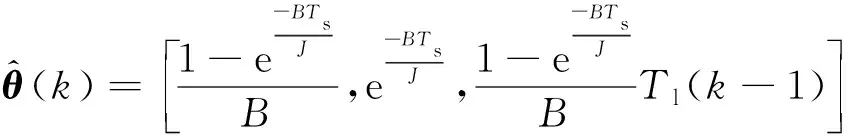
当Ts趋近于无穷小时，可得：

(10)

此时，系统可根据角速度ωm和电磁转矩Te为输入，依据FFRLS的递推公式可依次辨识出控制系统的转动惯量J与负载转矩Tl。

1.3 基于模糊控制的遗忘因子在线优化策略

FFRLS算法中的遗忘因子λ为恒定值，但λ的大小会影响算法的收敛速度和稳定性[17]。随着λ的增大，稳定性增强，收敛速度减慢，二者呈现出相反的趋势，常规选固定折中值的方法很难保证全工况条件下的稳定性和收敛速度得到较好的满足[18]。本文采用模糊控制理论对FFRLS算法进行优化，以解决FFRLS算法中结果收敛速度和稳定性相互矛盾的问题，以下为具体操作方法。

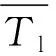
(11)

辨识过程中，|e(k)|越大，参数辨识模型与实际模型间差距越大，λ的值应减小，保证算法快速收敛；|e(k)|越小，参数辨识模型与实际模型间差距越小，λ的值应增大，提高算法的稳定性[19]。

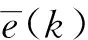
(12)

式中:m为选取残差的数量；Ts为仿真步长。

综上，基于模糊控制的遗忘因子在线优化的原理图如图1所示。

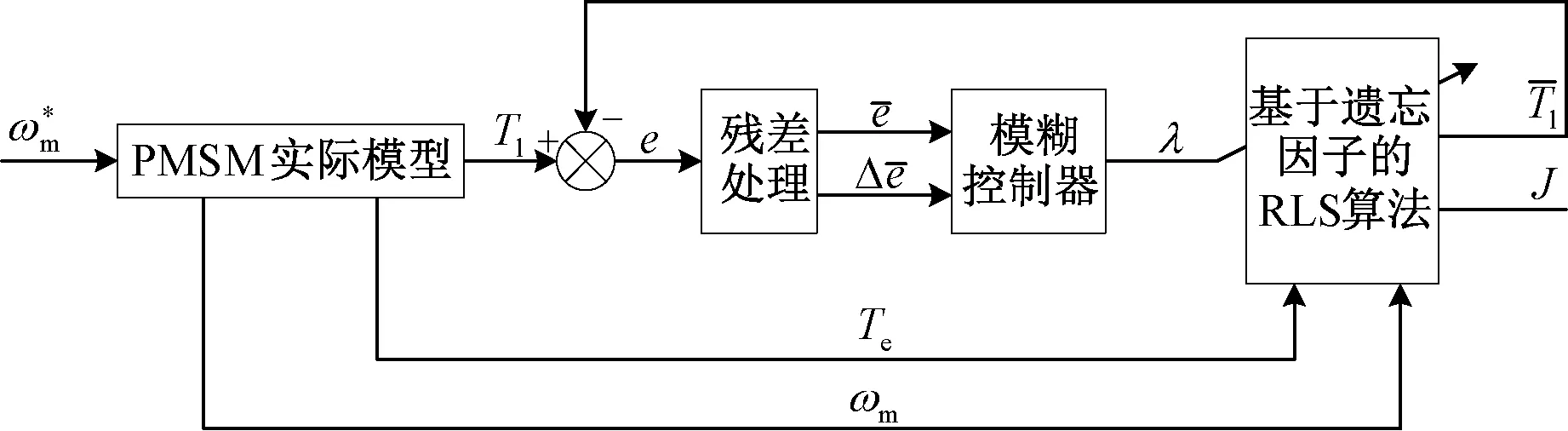
图1 基于模糊控制的遗忘因子在线优化

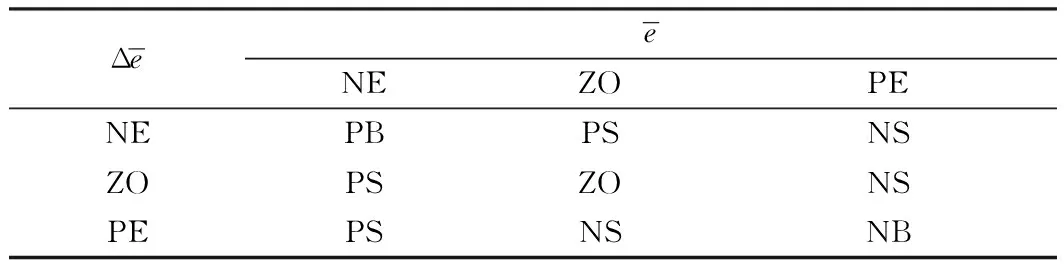
表1 模糊控制规则表

在实际转动惯量辨识过程中，为减少计算量，提高算法效率，支持算法实用应用，定义λ值的修正周期为仿真步长的α倍，第k时刻的辨识过程如图2所示。

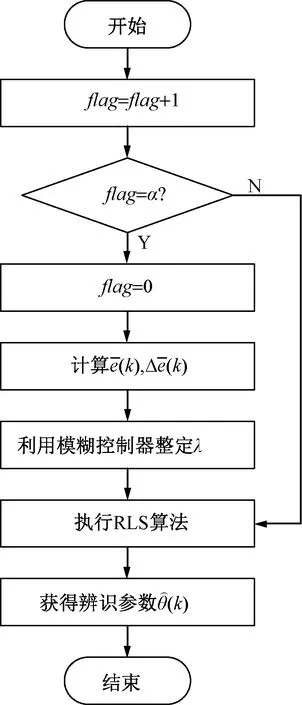
图2 第k时刻的辨识算法流程图

重复执行以上过程，即可实现PMSM系统转动惯量的在线辨识。

2 仿真分析

2.1 PMSM控制模型建模

在MATLAB/Simulink中构建表贴式永磁同步电机双闭环矢量控制系统，仿真电机参数来源于实验室自研的太阳能赛车用轮毂电机，主要参数如表2所示。图3为PMSM控制系统转动惯量辨识框图，在矢量控制系统基础上引入A-FFRLS算法，利用电机模型获得转速与转矩参数，完成算法的迭代计算，实现PMSM转动惯量的辨识。其中，仿真步长Ts=10-5s，仿真工况为太阳能赛车道路行驶最常用工况，转速800 r/min，负载为20 N·m。考虑到电机实际运行过程中，转动惯量在不同工况下的变化不明确，因此在仿真过程中以转动惯量的阶跃和渐变两种工况来验证算法的有效性。

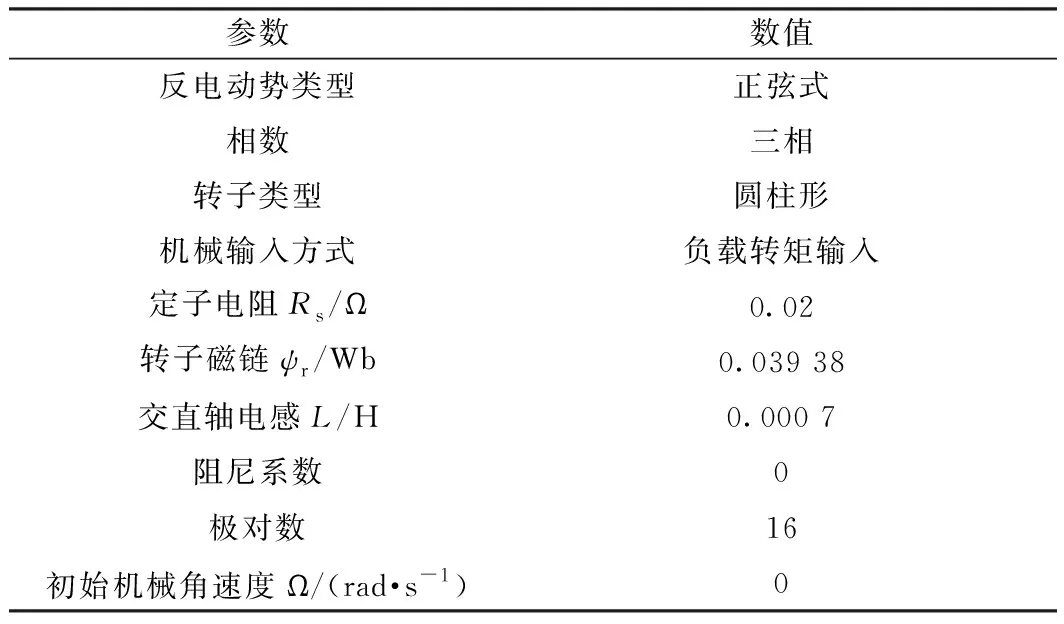
表2 电机模型参数表

基于图3的辨识模型，使用不同遗忘因子值的FFRLS算法对转动惯量进行辨识，对辨识数据的平均误差和平均方差进行分析，公式如下：

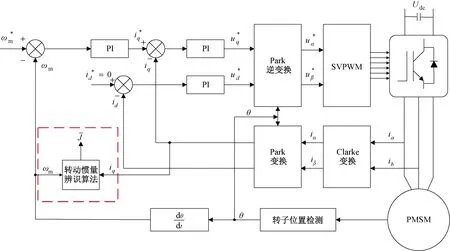
图3 PMSM控制系统转动惯量辨识框图

(13)

(14)

表3为不同遗忘因子值下的辨识结果，结果验证了FFRLS算法随着遗忘因子的值增大，辨识速度逐渐降低，辨识结果稳定性逐渐升高。取折中值λ=0.95作为算法的对比对象[19]，来验证A-FFRLS算法的有效性。

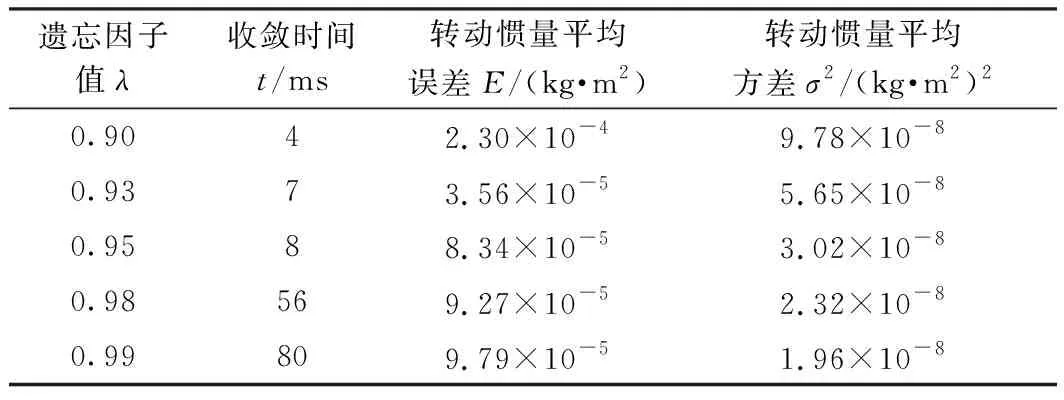
表3 不同遗忘因子下转动惯量辨识结果

2.2 PMSM转动惯量阶跃

PMSM在运行过程中可能出现负载激增，导致被控电机的转矩发生剧烈变化，此时转动惯量可能发生阶跃变化，因此建立电机在此种情况下转动惯量发生突增、随后重新稳定的仿真工况，旨在验证算法在电机转动惯量发生突变时的辨识效果。电机转动惯量参数变化如下：

(15)

图4和图5中设置电机转动惯量在0.2 s处发生突变，将A-FFRLS算法与λ=0.95的FFRLS算法进行对比，通过对比图4中转动惯量辨识曲线可发现，两种算法的收敛速度相差不大，均能在0.004 s之内收敛，但稳定性的差异较大。

图4 阶跃工况转动惯量仿真辨识结果

图5 阶跃工况遗忘因子变化

参考表4中所计算出两种算法辨识结果的平均误差和平均方差可得出结论：在阶跃工况下，A-FFRLS算法的误差和方差都更小、更稳定，曲线更平滑，在保证了收敛速度的同时，有效提高了算法的精度。

表4 阶跃工况转动惯量辨识结果

2.3 PMSM转动惯量渐变

电机转动惯量渐变过程模拟的是电机平稳工作时电机内部转矩等参数连续改变，从而影响转动惯量值发生连续变化并最终稳定的情况。仿真旨在验证A-FFRLS算法在电机转动惯量渐变时的辨识结果。电机转动惯量参数变化如下式：

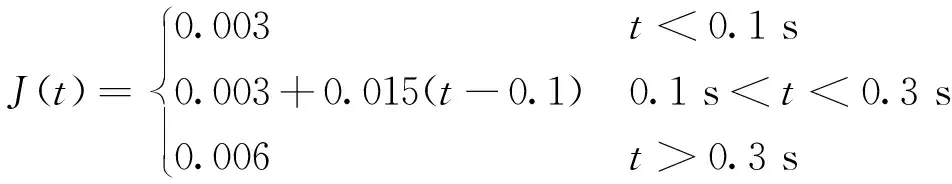
(16)

设置电机转动惯量值在0.1～0.3 s间渐变，将A-FFRLS算法与λ=0.95的FFRLS算法进行对比。通过图6可发现，两种算法的收敛速度相近，但稳定性存在较大差异，A-FFRLS算法的曲线波动要小得多。依据表5中计算出两种算法辨识结果的平均误差和平均方差，在渐变工况下，A-FFRLS算法相对于固定遗忘因子递推最小二乘算法辨识结果更加平滑稳定，更加有利于PMSM系统控制的稳定。

图6 渐变工况转动惯量辨识结果

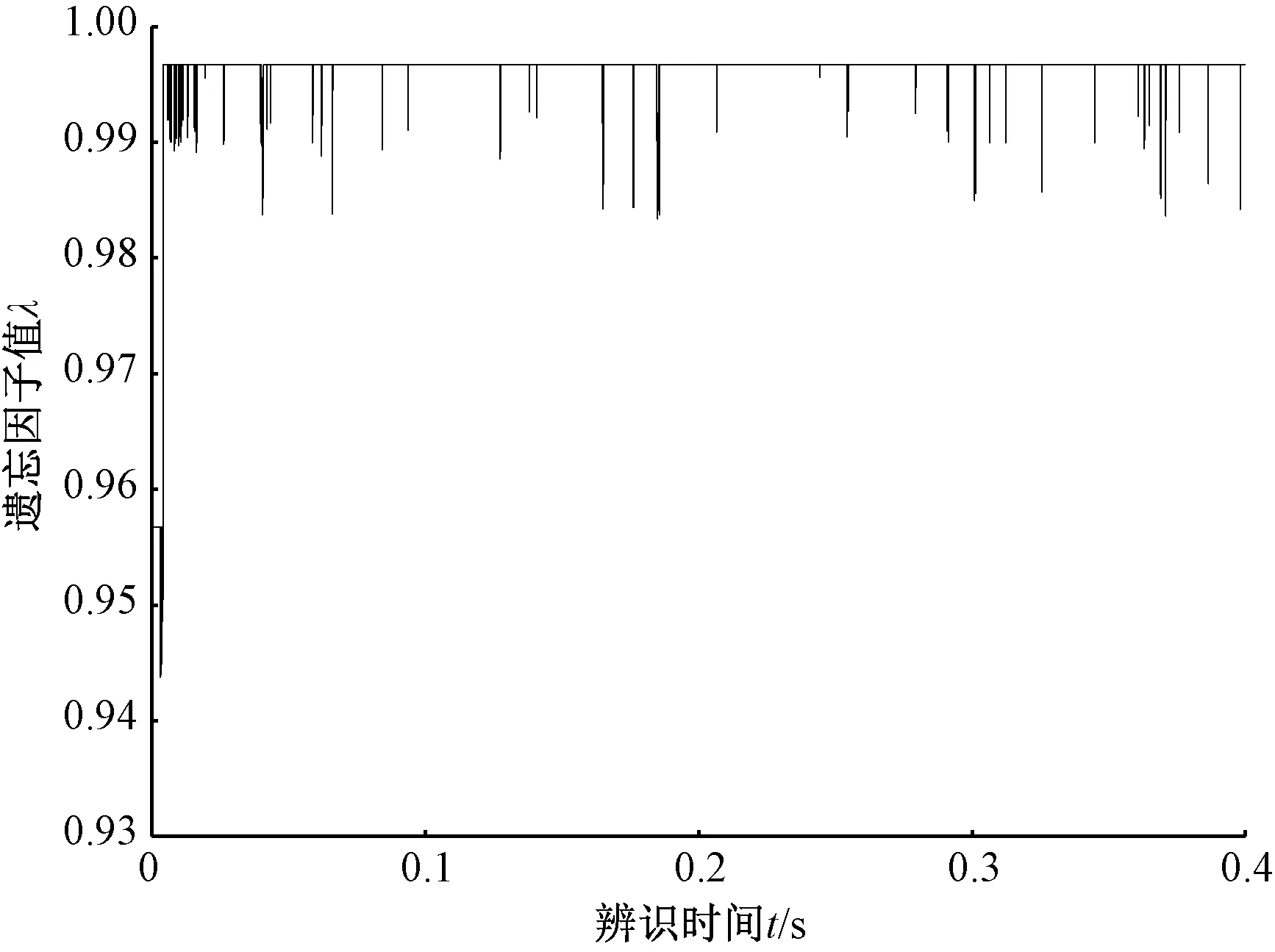
图7 渐变工况遗忘因子变化

表5 渐变工况转动惯量辨识结果

在以上两种情况下A-FFRLS算法相对一般的FFRLS算法在保证高收敛速度的同时，其辨识结果的误差和方差更小，具有更高的稳定性和精度，有效地解决了常规FFRLS算法中结果收敛速度和稳定性相互矛盾的问题，可实现PMSM转动惯量的实时辨识，为电机的调速控制提供参数依据。

3 实验验证

电机测试平台采用对拖形式搭建，图8为PMSM实验测试平台搭建示意图，图9为测试平台实物图。硬件主要由加载电机、被测电机、控制器和采集卡等组成，软件方面以LabVIEW为上位机，通过CAN通信的方式对2台电机进行控制，使电机能在特定的工况下运行。实验过程中，采用高精度转矩仪对实际的负载转矩与转速进行测量，并将信号传递给采集卡，由采集卡将转速转矩值传递到上位机，同时将A-FFRLS算法写入LabVIEW上位机，在上位机上进行算法的迭代计算，从而完成转动惯量的辨识。

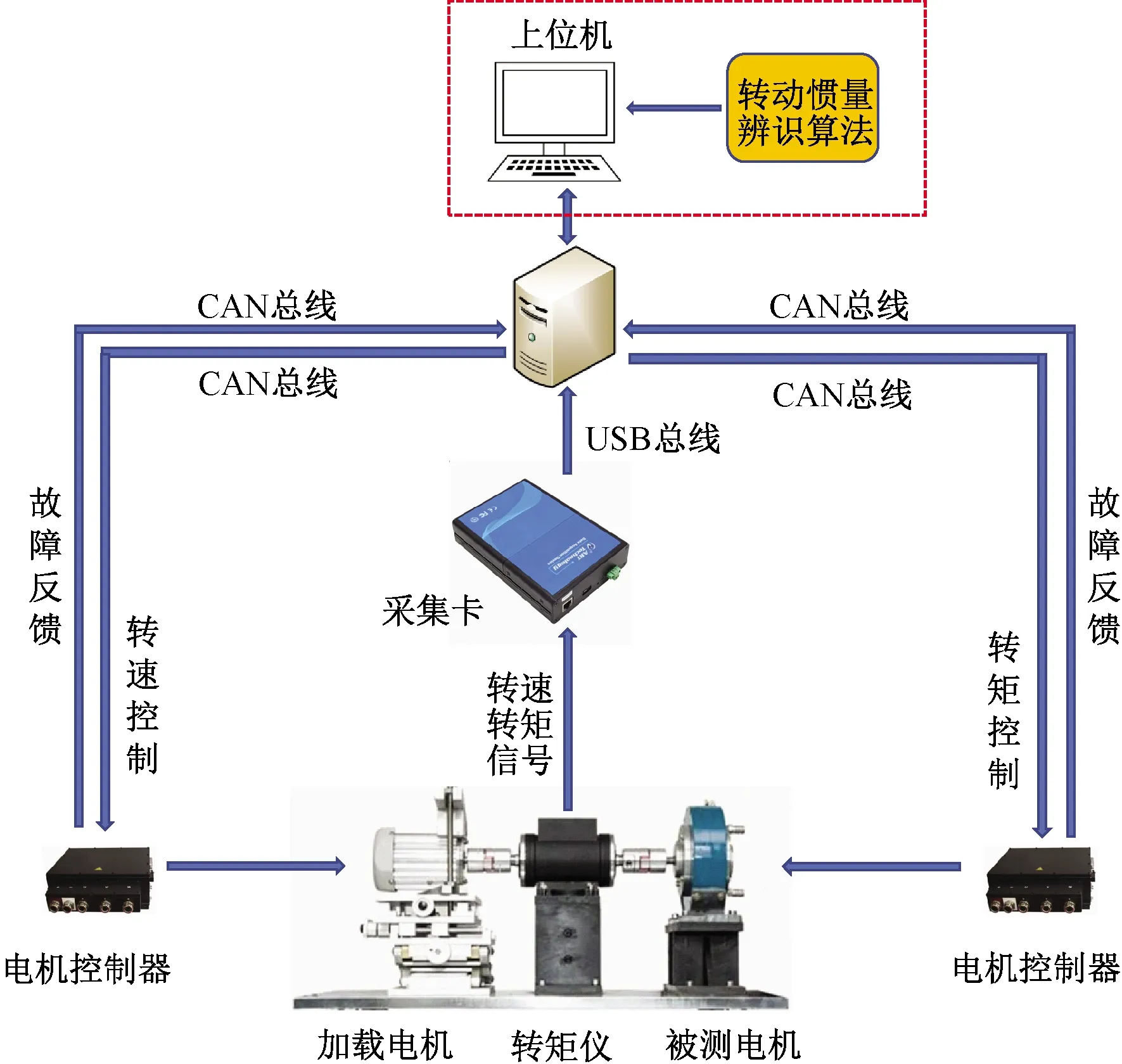
图8 PMSM实验测试平台搭建示意图

图9 PMSM实验测试平台实物图

为直观评估A-FFRLS算法的有效性，设计了负载突变工况作为实验工况。被测电机为太阳能赛车用轮毂电机，未加负载的情况下，通过电机和联轴器的尺寸和质量可计算出系统转动惯量约为0.002 kg·m2，电机的额定工况为转速800 r/min，额定转矩20 N·m，在行驶过程中单电机的峰值转矩能到30 N·m，综合考虑电机实际使用场景的需求，同时为验证电机在瞬态工况下算法的辨识能力，实验中通过CAN信号直接控制转矩的突变，将电机从空载突变为额定转矩再突变为峰值转矩的连续阶跃工况作为实验工况，即选择转速800 r/min，0.15 s时转矩由0突变为20 N·m，0.3 s处再突变为30 N·m，来对比A-FFRLS与FFRLS在负载突变时的辨识速度以及工况稳定后的辨识精度。与仿真不同，在进行实验测试时，转动惯量值无法人为设定，只能根据算法来进行辨识，同时由于外部干扰以及上位机实际计算处理能力有限等问题，实际辨识结果与仿真存在一定差异。实际的转动惯量辨识结果如图10所示，其遗忘因子值变化如图11所示。

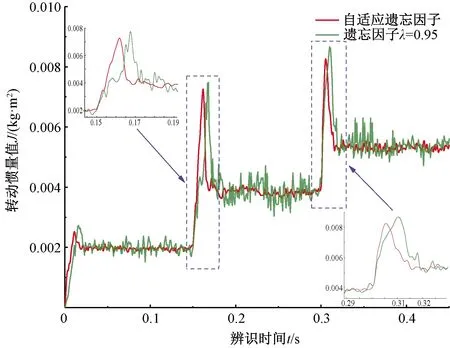
图10 实验转动惯量辨识结果

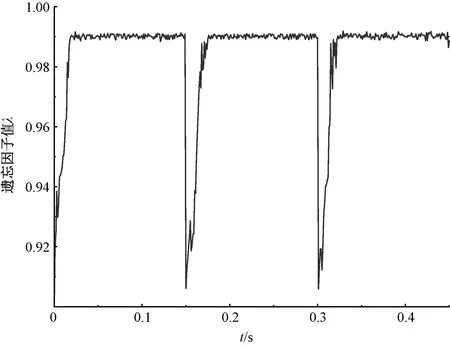
图11 实验遗忘因子变化

通过图10和图11可看出，电机负载分别在0.15 s、0.3 s发生阶跃突变时，所对应的遗忘因子值迅速减小，以提高算法收敛速度；当工况稳定后，A-FFRLS算法的遗忘因子值稳定为0.99，符合算法设计的预期效果。电机空载时，两种算法的转动惯量辨识值约为0.002 kg·m2，与实际计算出的结果一致，证明了算法的准确性；在负载发生突变的瞬态工况下，A-FFRLS相对于FFRLS算法的辨识速度稍快，在20 ms内辨识值即可达到收敛值。同时负载工况的不同会导致电机系统实际转动惯量的值发生改变，其辨识值从0.002 kg·m2突变为0.003 9 kg·m2再突变为0.005 3 kg·m2，以此值为标准计算出的两种算法辨识结果的平均误差和平均方差，如表6所示。在此种工况下A-FFRLS相对于FFRLS算法辨识平均误差能够降低50.2%，平均方差降低42.6%。

表6 实验转动惯量辨识结果

综上可知，在负载发生突变的瞬态工况下，A-FFRLS相对于FFRLS算法的辨识速度稍快；当工况稳定后，A-FFRLS算法的辨识结果更加准确和稳定，辨识曲线更加平滑，证明了本文设计的算法在进行转动惯量辨识时，解决了FFRLS算法中辨识结果收敛速度和稳定性相互矛盾的问题。在保证辨识速度的同时，具有更高的稳定性和精度，可实现PMSM转动惯量的实时辨识，为电机的调速控制提供参数依据。

4 结 语

为实现PMSM系统转动惯量的实时准确辨识，本文在FFRLS的基础上采用A-FFRLS算法以改善传统方法存在精度和实时性相矛盾的问题，同时保证了辨识具有良好的精度和实时性。本文在分析常规FFRLS算法优缺点的根本原因后，将FFRLS算法与模糊控制理论相结合，实现了遗忘因子的自适应控制。随后在MATLAB/Simulink平台上通过阶跃和渐变两种工况对比分析了A-FFRLS和FFRLS两种算法的辨识能力，证明了A-FFRLS算法的可行性和有效性。最后在电机测试平台上，依据电机的实际使用情况设计了负载瞬态突变实验，对比了两种算法下的转动惯量辨识效果。实验结果表明，在负载发生突变的瞬态工况下，A-FFRLS相对于λ=0.95的FFRLS算法的辨识速度稍快；当工况稳定后，A-FFRLS算法的的辨识结果更加准确和稳定，辨识平均误差能够降低50.2%，平均方差降低42.6%，可实现PMSM转动惯量的实时准确辨识，为电机的调速控制提供参数依据。