晚清汉译泽田吾一中学数学教科书初探

杜奇芳, 高红成

(天津师范大学 数学科学学院,天津 300387)

中国与日本同属汉字文化圈,文化交流源远流长。甲午战争之后,中国人看到日本明治维新的成功,认识到改变中国科举制度的重要性[1]。在这种社会背景下,清政府通过借鉴日本教育制度、派遣大批中国学生赴日学习、翻译和引进日本书籍、创办新式学堂等作为实现我国教育近代化的一条捷径。1904年,我国颁布《奏定学堂章程》(亦称“癸卯学制”),该章程几乎完全移植于日本,是我国最早付诸实施的近代学校章程。新学制颁布之初,各级各类学校所需的教科书极为匮乏,在这种情况下大量日本教科书被翻译引入,这些汉译日本教科书为新学制的顺利实施奠定了基础。数学作为必修课程,整个社会对数学教科书的需求迅速增大。据毕苑统计,1890年至1915年,汉译日本教科书书目共计27类507种,其中数学教科书所占比重最大共89种(算术类14种,代数类22种,几何类36种,三角类17种)[2]。据冯立昇教授统计,甲午战争后,清末翻译刊行的日本数学教科书的数量至少有151种,涵盖了从最初等的小学算术直到大学的微积分内容[3]。

当时汉译日本数学教科书底本主要是菊池大麓、长泽龟之助、藤泽利喜太郎、桦正董、上野清、林鹤一、泽田吾一等人的著作。学界对菊池大麓、长泽龟之助等人的数学教科书已有许多研究[4-7],比较充分,但对泽田吾一的研究不多,有些文章虽然提及却不系统和深入。通过初步研究和考证,泽田吾一共有6部数学教科书被翻译引入,包含算术、代数、三角学、解析几何、微分积分等方面,受众涵盖小学堂、中学堂和高等大学堂。从教科书种类和层次来看,仅次于长泽龟之助。泽田吾一的教科书翻译情况是研究新学制颁布后的数学教育发展的原始资料,值得关注和研究。限于史料和篇幅,本文简单介绍泽田吾一、教科书译者及出版社的情况,着重对其中几部中学数学教科书进行研究。

1 泽田吾一及其教科书译者简介

1.1 泽田吾一简介

泽田吾一(さわだごいち),1861年10月26日(文久元年9月23日)出生于日本岐阜市,1931年3月12日逝世,日本著名数学家、历史学者。明治15年(1881年)成为陆军省御用人员,在参谋本部测量科工作,同年加入东京数学会。1886-1887年在第一高等中学(现为东京都立日比谷高等学校)担任数学老师。1887年进入帝国大学理科大学物理系学习,著名数学家菊池大麓为其讲授数学,1891年毕业。1892年在第四高等学校担任教授,1896年任陆军中央幼年学校教授,1897年担任东京高等商业学校(现为一桥大学)教授,1917年退休。泽田一生都在不断学习。

泽田吾一曾在多所学校任教,教学经验丰富,曾编写多部数学教科书,如《高等小学笔算教本(教师用)》《高等小学笔算教本(学生用)》《解析几何学大意》《中等代数学教科书》《微分积分学纲要》《算术教科书》《商业算术教科书》《珠算练习实用算术》等,还与菊池大麓合编《初等平面三角法教科书》[8]。合作者菊池大麓(1855-1917)是日本明治时期的数学家、教育行政家,编写的数学教材非常丰富[9]。

因为泽田具有丰富的教学经验,他编写的数学教科书一定程度上可以说是数学教学思想与日本教学实践相结合的产物,在日本广受欢迎。当时接收清末留学生的日本成城学校,使用的三角学教科书就是菊池大麓、泽田吾一编纂的《初等平面三角法教科书》,这本教科书自1893年出版以来,到1905年已出日文版第五版订正本。此外还有泽田吾一任教的第一高等学校、高等商业学校都是清末留学生的培养机构。当时高等商业学校的数学教员就是泽田吾一,任教时间为1904-1905年[10]。可以想见,泽田吾一及其数学教科书在当时留日学生之间有一定的影响力,后来一些留日学生选择泽田的教科书作为底本也就顺理成章。癸卯学制颁布后,泽田吾一已出版的数学教科书基本上都被翻译引入我国,并逐渐进入我国课堂发挥其影响力。

根据调查和各书目,泽田吾一的数学教科书翻译引入我国的有6部,面向小学堂1部、中学堂4部、高等大学堂1部,大体情况见表1。

表1 汉译泽田吾一数学教科书Tab.1 Chinese version of Sawada Goichi’s mathematics textbooks

《笔算教本》为崔朝庆所译,底本是泽田的《高等小学笔算教本(学生用)》。张务本、赵宪曾合译的《最新代数学教科书》,底本是泽田的《代数学教科书》,有谷钟秀作的序和赵宪曾写的序言。王永炅译的《平面三角法新教科书》,底本是菊池大麓、泽田吾一合著的《初等平面三角法教科书》,黄元吉校订,书中翻译了原作者的序言。表1中第3部赵秉良译的《平面三角法》见于一些书目,可能是《平面三角法新教科书》的初版。彭延致译的《解析几何学纲要》,底本是泽田的《解析几何学大意》,仇壮嬴作序。这部教科书在各清末汉译日本数学教科书书目中未见记载,一些研究者也未曾注意,是本文新近发现的史料。赵缭译的《微分积分学纲要》,底本是泽田的《微分积分学纲要》,1907年初版,1910年再版。

1.2 译者简介

有些译者在清末时期名气与影响力较大,所以关于这些译者的研究文章或书目记载较多,如崔朝庆的生平资料就更容易搜集掌握。但还有些译者是之前学术界关注度不高的,现通过搜集史料在此做简单介绍。

崔朝庆(1860-1943),字聘臣,江苏南通人,清末民国时期著名的数学家、教育家,曾前往日本人在北京创办的同文书院学习,在此期间,他熟练掌握了日文,为日后翻译日文著作打下了良好的基础。1896年创办数学社团——集贤讲舍,1912年创办《数学杂志》[11]。

张务本、赵宪曾、谷钟秀三人为留日同学。张务本,山西大同灵丘人,基督教传教士,曾任“中华民国”奉天省(今辽宁省)高等检察厅检察长。

赵宪曾,直隶南宫县廪生,曾留学日本,习法政科[12],回国后,通过1909年廷试选拔成为外务部的司员[13],1917年(民国六年)任滨县县立第一小学校长[14],1920年任安徽省教育厅厅长[15]。

谷钟秀(1874-1949),字九峰,直隶定县(今河北定州)人,出生于直隶定州马家县,清末优贡。1898年,考入京师大学堂,1901年(光绪二十七年)赴日本早稻田大学学习政治经济学。留学期间,谷钟秀结识孙中山等革命党人,加入中国同盟会。回国后任直隶高等师范学堂教员、直隶督署秘书等。抗日战争胜利后,曾任北平市参议会议员、北平文物整理委员会主任委员、河北省政府民政厅厅长、河北通志馆馆长。著有《中华民国开国史》《世界地理》等[16]。

王永炅,留学于日本东京物理学校,毕业后回国,1907-1910年任闵学堂数理教习。曾在福建优级师范学堂讲授物化选课的初等数学和物理类科目。著有《新制算术校本》《新制平面几何学校本》《新制代数学校本》《新制平面三角法校本》《新制立体几何学校本》《数学公式》等,大都为中学校及师范院校适用[17]。

黄元吉,曾在上海商务印书馆担任编译工作。编写《共和国数学教科书》《中学代数学教科书》《中学校教科书平面几何》等。黄元吉翻译的日本数学著作主要有:林鹤一、津村定著《代数学:因数分解》; 林鹤一、谈中济著《算术——整数及小数》; 东利作著《平面几何学——圆》; 林鹤一、武田登三著《平面几何学:面积》; 林鹤一、淡中济、大冢驵太郎著《算术:分数四则》; 林鹤一、矢田吉熊著《代数学:幂法开法及无理数虚数》; 林鹤一、菅集人著《平面几何学:直线图形》; 菊池大麓著《平面几何学教科书》等。这些翻译的数学著作都被囊括在《算学小丛书》中,并被收录在《万有文库第一集》。

本研究通过比较学龄期ALL患儿自评和家长代评生活质量得分，了解了ALL患儿整体生活质量状况;也进一步证实患儿和家长总体评价间不存在明显差异，当患儿自评存在困难时，家长代评具有一定的参考价值;并且提示了在临床工作中，应充分结合患儿和家长两者的汇报，以提供更全面、更优质、更个性化的护理。

赵缭(1878-1952),字负沉,长沙人。20世纪初进入由岳麓书院改制的湖南高等学堂。1903年进入日本弘文学院,学习日语、修身、教育学、数学、理化、史地等科目,不久升入大阪高等工业学校。1905年8月在日本加入同盟会。曾被吉林省高等学堂聘为教授,任教数学、天文学等课程[18]。参与翻译的日文书籍有《微分积分学纲要》(泽田吾一著),与余焕东合译《新译算术教科书》(桦正董著),与易应崐合译《中学校数学教科书算术之部》(桦正董著)《中学校数学教科书算术之部问题详解》《中学校数学教科书代数之部》(桦正董著); 与易应崐合编中学教科书《算数之部》《代数之部》。

有关彭延致与仇壮嬴的生平资料未找到,但从《解析几何学纲要》的序中得知,两人为同学。书中的序是仇壮嬴在1911年于东京之客邸所作,以此推断彭延致和仇壮嬴应该都为留日学生。

2 《平面三角法新教科书》简介

《平面三角法新教科书》的编排顺序为:序言、目录、公式集锦、正文内容、附录、习题答案、对数表、圆函数对数表、圆函数表。从序言中可以得知,菊池大麓和泽田吾一于1891年开始合编该教科书,于1893年初版完成,日文原版在1893年由大日本图书株式会社出版发行。该书每次再版,都详加修正。如1899年的修订版中,将百分法、弧度法、正矢、余矢、逆圆函数删略。1905年已出日文版第五版订正本。此外“序言”中明确指出该书的使用范围,即中学校教科书体裁。菊池大麓与泽田吾一称这本书“比其他三角法书,不无稍异其趣”,但“约言处尚多,必待教员推勘说明,乃是完全无遗憾”。且原著者认为该书论述简洁,较注重实用性。

编排形式上完全按照西方数学教科书的形式,采用横排编写,利于公式的书写。同时,在学生容易忽略的地方,标有“注意”二字,并加黑,以便提醒学生易错之处。编写过程中注重图文,正文中有三处地方应用了表格说明,使所述内容直观明了。书中有丰富的图形,许多例题、公式通过图形来推理说明,比如圆函数正负记号,任意之角、之圆函数等都通过图形推理说明,清晰明了,便于记忆。

《平面三角法新教科书》中“公式集录”列有70组公式,共有公式124个。书中的定义、公理、定理都采用统一编号,每节习题重新排序,且习题均在书后附有答案,便于学生学习。全文共十五编,依次为:

第一编:角之计算法; 第二编:圆函数; 第三编:30°45°60°; 第四编:任意之角; 第五编:余角外角圆函数之关系; 第六编:二角之圆函数; 第七编:倍角之圆函数; 第八编:三角方程式; 第九编:分角; 第十编:对数; 第十一编:对数及三角表之用法; 第十二编:三角形角及边之关系; 第十三编:三角形解法; 第十四编:距离及高; 第十五编:三角形面积,外切圆,内容圆。

《平面三角法新教科书》的附录“测量大意”包括六章内容,分别为:侧链测量、罗针盘测量、罗针子午线、真子午线、经纬仪、三线测量、水准测量。所占篇幅为21页。每一章均从具体实例出发,利用三角函数知识对实际问题进行求解。对于附录中的内容,序言中说:“三角法应用之最著名最近便者,莫如测量。测量之为术,在受中学教育者,颇适切于实用,且于学者亦大增趣味。故于其学三角法而以实用示之者。必行利便。”

卷末所附对数表、圆函数对数表、原函数表所占篇幅并不多,目的是让学习者用于练习,而非专门用于计算的检查捷表。关于三角计算表:“行世既多,组织各异。有列比例部分一行或二行以上者,有附列比例部分小表或亦有不附列者。本书之表,固求其具备,悉心编成者也。”关于圆函数对数表:“差值变化过大者,用五分进法,其缓者用十分进法。故由此表所得之数,比由一分进表所得者,不无小异,惟其差甚微。以实地验之,只是不足争之小数耳。”此外书中还强调,对近于0°及90°的角,其圆函数必当依密表检算[19]。

3 《最新代数学教科书》简介

《最新代数教科书》上册的编排顺序为:代数学教科书序、序言、凡例、目录、正文、补习问题、附录、答之部,共69个知识点,83道例题,745道习题。下册的编排顺序为目录、正文内容、附录、补习问题、答之部、版权所有页、河北译书社印行书目,共73个知识点,89道例题,555道习题。采用横排编写,利于公式的书写。阅读顺序为自左向右,对于方程式及其代数式也采用横排编写,大大简化了教科书的内容,方便实用,简明扼要。

从书中开篇的序中得知,谷钟秀认为代数学从西欧传入我国,可通过我国已有的天元术知识进行领悟学习。当时代数学已成为中学重要教科,但是“应用则略揆,诸教学之道有遗憾焉”。而泽田吾一的代数学教科书恰恰弥补了这一缺点,并且赵宪曾与张务本认为,泽田吾一所著教科书在代数学方面是“尤善之善者”,故赵氏与张氏选择泽田吾一的代数教科书进行翻译。

在正文目录之前,有七条凡例如下[20]:

(一) 旧代数学,用干支及天地等字代既知及未知数。是书悉用罗马字母代之,循各国教科之通例。我国近自中学以上亦置英文一科,习此亦甚便,故仍之。

(二) 旧代数学,尽直行书之。此用横行,从算术教科等书之例,以归一致。

(三) 中东文字虽同,而义意逈异,故遇其不能猝解之字悉改用吾国常语,以使学者易读。

(四) 创作名词,系著者第一之工夫。故其确正名词,稍思索而能得其意者,仍采用之,以存原著本色。

(五) 教科书为教育本国国民而作,原书问题,间有不适吾国用者,易之。

(六) 中东度量权衡不同,故关于此等之问题,悉尊吾国之度量权衡法而改正之,使无歧误。

(七) 译书易蹈辞不连意之弊,此书辞笔务避艰深,以平易为主,尚祈学者不以浅近见讥,是幸。

这七条凡例大体概括了张务本、赵宪曾在翻译数学教科书时的标准:引进西方数学符号代替汉字天干、地支等,已知及未知数均用罗马数字代替汉字甲、乙、丙、丁等; 采用横排编写的方式代替原有的竖排编写,阅读顺序为自右向左; 虽然中国与日本的某些字形同但意义迥异,在翻译时应采用我国常用语,方便阅读; 能够通过字面本身而领悟其含义的术语,要保留原著本色; 原书中的问题需符合我国国情,对于不符合者应删略; 我国与日本度量权衡标准不同,翻译时以我国为准; 译述的语言应浅显易懂,忌深奥晦涩。这些准则在当时对教科书的编译有重要的借鉴和引领意义。

《最新代数教科书》正文共十三编,上册六编,下册七编。书中正文内容为:第一编绪论; 第二编整式; 第三编方程式; 第四编整式续编; 第五编分数式; 第六编方程式续编; 第七编二次方程式; 第八编无理式; 第九编比及比例; 第十编级数; 第十一编顺列及配合; 第十二编二项式定理; 第十三编对数。与下册相比,上册每一编之后都附有杂题。全书在学生容易忽视的地方,标有“注意”二字。涉及加法、减法、乘法等章节内容时标有“法则”二字。在例题解答过程中,对结果进行验算时,标有“验”字并用下划线强调。整体来看,书中每章内容基本上均采取了叙述式的编写体例,即以概念-公式、方程或法则-例题-习题的形式呈现。

4 《解析几何学纲要》简介

《解析几何学纲要》的编排序言为:绪言、上海群益书社新书广告两页、目录、正文、问题之答。全书共89个知识点,116道习题。横排编写,页码采用阿拉伯数字编号。仇壮嬴认为“虽然世固有明微积之理而不明大代数学者,未有明微积之理而不明解析几何学者矣”[21]。也就是说他认为明晓解析几何是学习微积分知识的基础,甚至评价道“无几何学则微积分学空虚而无用”。

《解析几何学纲要》中的内容分为九部分,前八部分为正文,后一部分为问题之答,共113页。《解析几何学纲要》的目录为:第一编“点”,15页; 第二编“直线”,22页; 第三编“极坐标”,7页; 第四编“坐标之变换”,6页; 第五编“圆”,19页; 第六编“圆锥曲线”,19页; 第七编“一般二次方程式”,6页; 第八编“点,直线,平面,曲面,(立体几何学)”,10页; 问题之答,9页。

泽田吾一在原著的绪言中,对此书做以下评价:

本书结构与历来书籍有诸多不同之处。许多所称解析几何学的书籍更注重对圆锥曲线的研究,但这只是由于圆锥曲线的性质在一定程度上是讲授解析法的好材料罢了; 依编者见,如圆锥曲线的复杂性质,对于不是数学专家的人来说并无大用处,而解析法才是能让广大一般人士大受裨益之物; 故而,本书对于初学者的解析法中最有效的部分,即线与圆的论述较多,而对于圆锥曲线,只给出了其重要性质及简单定理,并将一般相对复杂的部分省略(但在问题中也给出了一些)。

由此可见,此书编撰的目的是为了简便,这对解析几何学的的思想传播与普及有积极的促进作用。

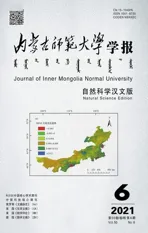
但《解析几何学纲要》在各大书目中未见记载。书中的一个重要的特点是,数学名词术语后面带有英文原版名词,在名词后加上英文原名,统一名词术语,为熟习英文的学生提供方便,不致概念混淆。全书共59个学术名词,其中大部分名词术语与现今所用术语完全一致或相近。不太一致的数学名词如表2所示。

表2 《解析几何学纲要》一些名词术语译文Tab.2 Translation of some terms in Outline of Analytic Geometry

5 结语

泽田吾一的三种中学数学教科书的传入,正逢清政府施行《奏定学堂章程》时期,因此这些数学教科书无疑最符合当时的教育国情。由于资料限制,本文只涉及泽田吾一的中学数学教科书,对于他的《微分积分学纲要》只有付之阙如。汉译泽田吾一中学数学教科书改变了以往长期从右至左的编排习惯,完全采用西方数学教科书的编排形式,采用西方数学符号,如书中的没有采用天、干、地、支、人、口甲、口乙、口丙、口丁等晚清数学家李善兰和伟烈亚力主创的数学符号,而是用西方字母A、B、C来表示,同时还采用了现代数学符号+、-、×、÷等。名词术语翻译是否准确,对于知识的传播与理解有重要影响,书中的大部分数学名词术语与现在一些数学名词术语相近或相同。此外,教科书中的定义、定理也简洁明了,习题丰富,例题也做到每一步都简洁易懂。内容安排注重实用性,将理论与实际相结合,让学生学以致用,难度适中,方便学生的自学。这些特点让学生的学习更加方便化、系统化,对当时中国数学教育的发展走向近代化起到了直接的促进作用。