城市道路平曲线设计指标探究

董占宇

（上海市政工程设计科学研究所有限公司，上海市 200092）

0 引 言

城市道路平面走向一般遵循规划红线，在路线转角处往往需设置平曲线。《城市道路路线设计规范》（CJJ193—2012）（下文简称《规范》）中对于平曲线设计指标进行了具体的规定。但在实际工程设计中，尤其是路线转角较小时，设计人员对于《规范》中部分条文的解读常常产生分歧，一定程度上降低了工程设计效率。对《规范》中相关平曲线设计条文进行分析，厘清不同条文的适用条件，选取合适的设计指标，对于提高设计效率、保证工程质量具有积极的意义。

1 平曲线参数计算

1.1 道路平面线形

直线、圆曲线和缓和曲线，称为平面线形三要素，世界各国道路平面线形均由三要素组成。其中，圆曲线与缓和曲线统称为平曲线。

缓和曲线的形式较多，包括回旋线、三次抛物线、双纽线、多次抛物线等等。世界各国使用回旋线居多，根据《规范》，我国城市道路中缓和曲线也采用回旋线。

1.2 回旋线基本公式

回旋线是曲率随曲线长度成比例变化的曲线，这一性质与驾驶员以匀速转动方向盘汽车由直线驶入圆曲线或圆曲线驶入直线的轨迹线相符[1]，其基本公式为：

式中：r为回旋线上某点的曲率半径，m；l为回旋线上某点到原点的曲线长，m；A为回旋线参数，m。

在回旋线终点处，l=Ls，r=R，则有：

式中：R为与回旋线相连接的圆曲线半径，m；Ls为回旋线长度，m；

1.3 平曲线几何元素计算

以城市道路平面线形中最为常见的对称基本型曲线为例，其计算图式见图1。

其几何元素计算公式如下[1]：

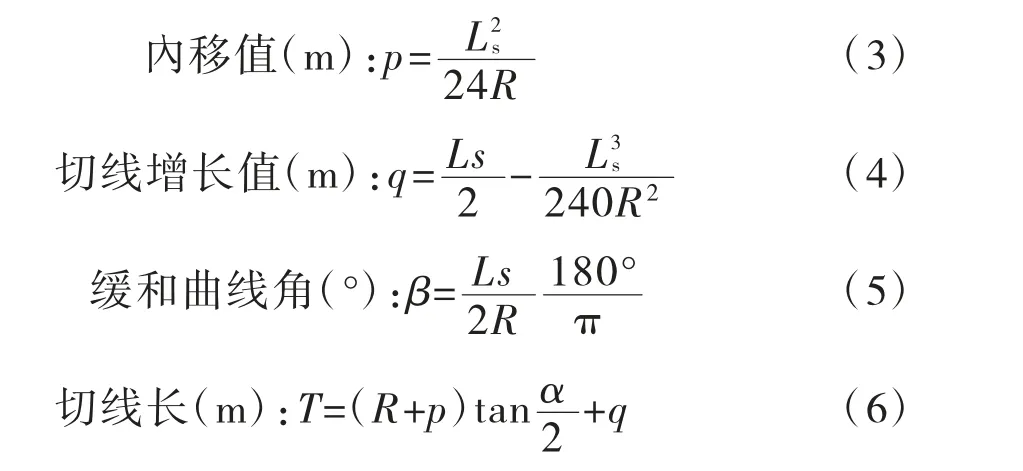
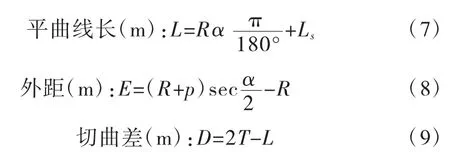
式中：Ls为回旋线长度，m；R为圆曲线半径，m；Α为转角（°）。

2 《规范》中平曲线设计指标相关条文

《规范》中对于城市道路平曲线设计指标的规定较为详细，本文中不一一列举，仅列出实际设计过程中经常产生分歧的几条：

（1）《规范》条文6.3.3第5款：缓和曲线最小长度应符合表1的规定。当圆曲线按规定需设置超高时，缓和曲线长度还应大于超高缓和段长度。

表1 缓和曲线最小长度

（2）《规范》条文6.3.3第6款：缓和曲线参数A宜根据线形要求和地形条件确定，并应与圆曲线半径相协调，宜满足R/3≤A≤R的要求。当圆曲线半径小于100m时，A宜接近R；当圆曲线半径大于3000m时，A宜接近R/3。

（3）《规范》条文6.3.4第1款：平曲线与圆曲线最小长度应符合表2的规定。

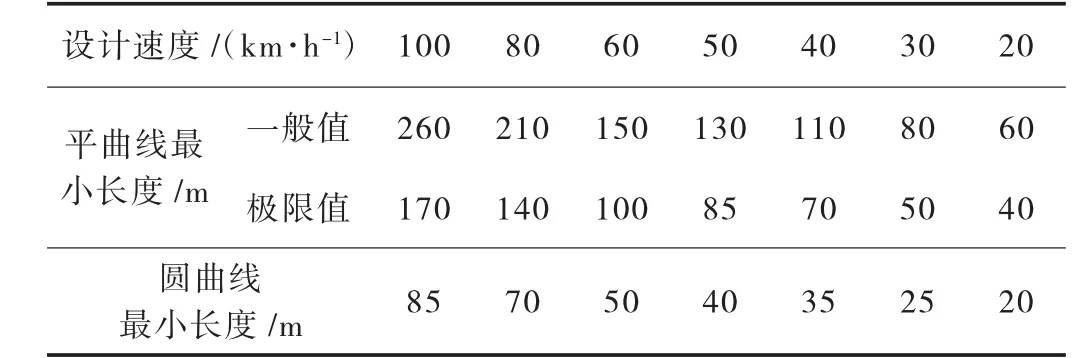
表2 平曲线与圆曲线最小长度

（4）《规范》条文6.3.4第2款：道路中心线转角α小于或等于7°时，设计速度大于或等于60km/h的平曲线最小长度还应符合表3的规定。

表3 小转角平曲线最小长度

此外，《规范》中未提及，《公路路线设计规范》（JTGD20—2017）条文9.2.4第1款要求，对于基本型曲线。

（5）回旋线—圆曲线—回旋线的长度以大致接近为宜。

一般来说，按第（5）条要求，将回旋线、圆曲线、回旋线的长度之比设计成1∶1∶1～1∶2∶1[1]，这种线形在视觉上较为协调，故该条文也经常作为部分设计人员遵循的标准。

3 相关条文解读

3.1 缓和曲线最小长度的确定方法

从驾驶操作的角度考虑，一般认为汽车在缓和曲线上的行驶时间不少于3s，才能使驾驶员从容地转动方向盘。若设计速度为v（km/h），则

从乘车感受的角度考虑，设αs为离心加速度变化率，以直线与圆曲线（半径为R）之间的缓和曲线为例，设在t（s）时间内汽车由缓和曲线起点行驶至缓和曲线终点，离心加速度由0变化到v2/R，而t=Ls/v，于是有

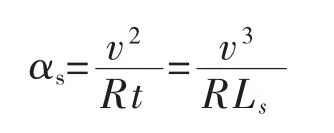
我国离心加速度变化率采用0.6m/s3，故从乘车舒适性角度计算，要求

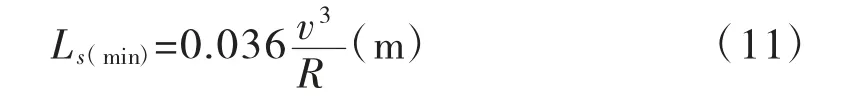
R选用设超高最小半径，对式（10）和式（11）分别验算后，取两者中大值，并取整为5或10的倍数，即可得到表1中的结果。

3.2 平曲线最小长度的确定方法

根据经验，在每段曲线上驾驶员操作方向盘不感到困难至少需要3s的行程。如果中间圆曲线长度为0，平曲线长度也需要达到缓和曲线最小长度的2倍，此时两段回旋线径向衔接，曲线为凸形曲线，对驾驶操作不利，而且视觉上也不舒顺，只在路线严格受地形、地物限制处方可使用，表2中平曲线最小长度极限值即按此控制。

为了避免驾驶员频繁操作，引起驾乘体验的不适，平曲线最小长度一般值按照3倍于缓和曲线最小长度控制，即保证两端设置最小长度的缓和曲线后，保留一段相同长度的圆曲线，使车辆通过圆曲线的时间不小于3s，由此得到表2中平曲线最小长度一般值。

当平曲线转角太小时，即使采用较大的圆曲线半径，驾驶员仍会将曲线长度看成比实际的短，造成急转弯的错觉，转角越小，这种现象越明显。根据经验，引起驾驶员错觉的道路转角临界值为7°。为了使驾驶员在小转角平曲线上准确识别出路线的实际情况，需设置足够长的平曲线，增大曲线的外距。若平曲线最小长度仍按两端缓和曲线径向衔接控制，此时即有

将式（12）带入式（7）得到：

当α很小时（≤7°），sec(α/2)接近1，根据式（8），可以近似认为E≈p，将式（12）、式（13）带入式（3）得到：

α＜7°时，为尽量消除小偏角路线可能引起的驾驶员视觉误判，需使平曲线外距E与α=7°时的E相等。若α=7°时，L按非小偏角平曲线极限最小长度（6s行程）控制，即L=v/0.6，根据式（14），应有

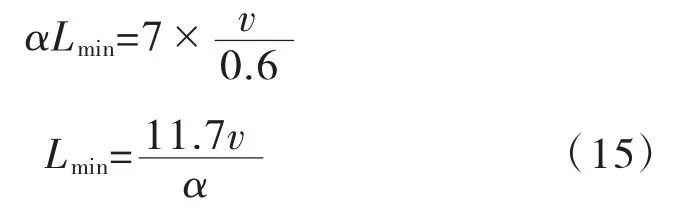
将设计速度数值代入式（15）计算后取整，即可得到表3中的结果。

3.3 缓和曲线参数A的确定方法

缓和曲线的设置不仅使车辆更易于遵循车道轨迹，同时也使线形连续圆滑，能更好地诱导驾驶员视线。为了获得视觉上美观、舒顺的线形，缓和曲线角β宜控制在3°～29°之间，将β=3°及β=29°代入式（2）、式（5），则有即

若R小于100m，则A宜大于或等于R；当R接近100m时，宜取A=R；当R较大或接近于3000m时，A宜选择在R/3左右；当R超过3000m时，即使A小于R/3，视觉上也是舒顺的。

3.4 条文优先次序分析

规范用词的角度分析，第2章中所列第（1）、（3）、（4）条均采用“应”字，表示严格，在正常情况下均应这样做；第（2）条采用“宜”字，表示允许稍有选择，在条件许可时首先应这样做；而第（5）条未在《规范》中列出，在实际设计过程中，可以根据实际情况自由选择是否遵循。

从实际应用的角度分析，第（1）、（3）、（4）条对车辆行驶安全影响较大，工程设计中平曲线指标必须首先满足其要求；第（2）条主要从线形的顺适与美观角度考虑，对行车安全影响较小，条件受限时，可适当放宽；第（5）条的提出也是基于视觉上线形的协调考虑，虽然《规范》中未作此类要求，但在道路工程设计中，在满足行车安全的基础上，追求线形的美观、协调是值得鼓励的，故在实际应用中第（5）条可作为参考，但条件受限时可不必强求。

根据以上分析，本文所列举出的条文优先次序应为：（1）=（3）=（4）＞（2）＞（5），见表4。

表4 条文优先次序

4 不同条件下平曲线设计指标探究

4.1 条文适用的边界条件分析

根据图1可知，设置基本型曲线的几何条件为：

城市道路平面线形受到规划红线的限制，路线转角α不能自由调整，而且城市中小转角的情况比较普遍，所以缓和曲线角β的设置也受到一定限制。实际设计中，特别是遇到小转角平曲线，经常出现本文所列条文无法同时满足的情况，比如：有时无论采用任何方法，A值都无法取到R/3；有时A值取到R/3，但平曲线长度不满足一般值要求。故应对各条文的适用条件进一步分析，在选用条文时有所取舍。

对于条文（1）、（3）、（4），无论路线转角α大小，选用合适的圆曲线半径及缓和曲线长度，均易于满足，主要矛盾集中在第（2）条和第（5）条。

根据式（16）、式（17）的推导过程可知：

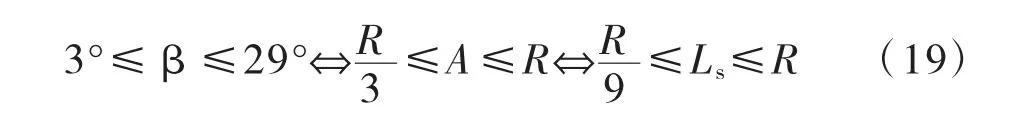
故若A≥R/3，则缓和曲线角β需大于等于3°，由式（18）可知，需α≥6°。换言之，规划红线的路线转角α需在6°以上时，缓和曲线参数A才有按条文（2）推荐的范围取值的可能性。

由图1和式（5）可知，设圆曲线长度为LY，若要满足第（5）条Ls1∶LY∶Ls2在1∶1∶1～1∶2∶1之间，则需

结合式（19）可知，规划红线的路线转角α需在12°以上时，才有同时满足第（2）条和第（5）条的可能性。根据以上分析，α=6°及12°是对条文取舍的边界条件，对于不同的α，应具体分析需要遵循哪些条文、无需或不能遵循哪些条文，防止本末倒置的情况出现。

4.2 α≤6°时的平曲线设计方法

当根据规划红线走向确定的α小于6°时，β必然小于3°，所以这种情况下无论如何也无法满足第（2）条。当α=6°时，若满足第（2）条使β=3°，则圆曲线长度为0，平曲线为凸形曲线，驾驶员操作频繁，对行车不利。

α≤6°时往往需要设置较大的圆曲线半径才能满足平曲线长度要求，即使缓和曲线参数A不满足第（2）条中推荐的范围，平面线形也是舒顺的。所以这种情况下可不必考虑第（2）条，在满足（1）、（3）、（4）的基础上，尽量满足第（5）条的要求。

由于此时圆曲线半径经常大于《规范》中规定的不设缓和曲线最小半径，故也可以只设置圆曲线。虽然第（4）条的结果是考虑设置缓和曲线的条件下计算得出，但经过对仅设置圆曲线情况下外距的验算，圆曲线长度按第（4）条控制是可行的。

4.3 6°＜α＜12°时的平曲线设计方法

当6°＜α＜12°时，缓和曲线参数A具备了按照第（2）条推荐范围取值的基本条件。当α与圆曲线半径R确定时，由图1可知：LY=R（α-2β）π/180°，缓和曲线角β的大小影响圆曲线长度。如果β过大，而R又不足，将导致圆曲线长度不足。故在满足第（2）条中β≥3°的要求时，需要设置半径足够大的圆曲线，才能满足条文（3）中对平曲线最小长度一般值的规定。而城市道路圆曲线半径受规划红线限制，所以应结合用地条件，对于不同半径的圆曲线，分析各条文的适应性。

设条文（1）中规定的缓和曲线最小长度为Ls（min），条文（3）中规定的平曲线最小长度一般值为Lmin，令圆曲线最小长度LY（min）=Lmin-2Ls（min）应注意Ls（min）≈LY（min）。通过计算可知，α＞6°时，Lmin均能满足条文（4）的规定，故此时平曲线长度按条文（3）中一般值控制即可，无需考虑条文（4）的规定。

可以注意到，当6°＜α＜12°时，若满足条文（2），令β≥3°，则有β＞α/4，此时缓和曲线长度必然大于圆曲线长度。所以此时只要保证LY≥LY（min），即可满足条文（3）中对平曲线最小长度一般值的要求（因为此时Ls＞LY≥LY（min）≈Ls（min），即R（α-2β）π/180°≥LY（min），将β≥3°代入可得到满足条文（1）、（2）、（3）（一般值）、（4）时关于圆曲线半径的必要条件：

若根据用地条件拟定的圆曲线半径满足式（21），则可判定该交点处有条件按条文（1）、（2）、（3）（一般值）、（4）的要求设置平曲线。根据式（20），在这种情况下，第（2）条与第（5）条的要求实际上是矛盾的，而（2）的优先级别高于（5），所以应优先遵循第（2）条，不再考虑第（5）条的要求。

但当平曲线转角很小且平曲线设置不受用地限制时，采用式（21）计算出的圆曲线最小半径动辄上万米、缓和曲线长度动辄上千米，过长的曲线不利于施工计算与放样，线形比例也不协调，所以当R大于不设缓和曲线最小半径时，应取消缓和曲线，仅设置圆曲线，满足（3）、（4）即可。

如果由于用地条件限制，可设置的最大圆曲线半径R无法满足式（21）（见图2），即LY（min），意味着β=3°时，LY≥LY（min），如果要保证LY≥LY（min），则需β＜3°，此时条文（2）与条文（3）（一般值）的要求产生了矛盾。根据前述分析，圆曲线半径及长度应是影响行车安全的首要因素，设计过程中不应牺牲圆曲线长度去满足缓和曲线角的要求。但即使不考虑β的大小，圆曲线半径也应达到一定值才能使L≥L（min）且LY≥LY（min），故需对条文（3）中L≥Lmin的 要 求 进 行 一 般 性 验 算。将L=LY+2Ls，Ls≥Ls（min）、LY≥LY（min）及Ls（min）≈LY（min）代入式（7）可得：

图2 大半径圆曲线超出用地限制

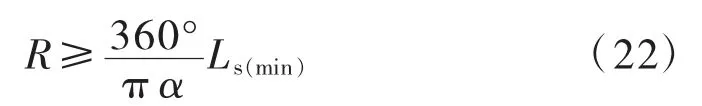
式（22）即为平曲线长度不小于条文（3）中一般值的基本条件。若根据规划红线拟定的圆曲线半径R满足，且 半 径 较大（接近3000m）的情况下，可不考虑条文（2），平曲线设计指标按（1）、（3）（一般值）、（5）控制即可；半径不大的情况下，应在满足圆曲线长度的基础上尽量贴近（2）的要求，取，使β尽量接近3°，此时无需考虑第（5）条的要求。

若由于用地条件限制，可设置的最大圆曲线半径R仍无法满足式（22），即则在设计速度不变的情况下，平曲线长度只能考虑按极限值控制（此时不具备满足第（5）条的条件）。即便如此，圆曲线半径也应达到一定值，才能使平曲线长度不小于条文（3）中的极限值：

式（23）为平曲线长度不小于条文（3）中极限值的基本条件。如果根据用地条件所能拟定的最大圆曲线半径R不能满足式（23），则必须采取降低设计速度、调整规划红线（以调整圆曲线半径）等措施进行重新设计、验算。

4.4 α≥12°时的平曲线设计方法

当α≥12°时，平曲线指标具备了同时满足（1）、（2）、（3）、（5）的基本条件，但圆曲线半径仍需满足式（22），才能使平曲线长度按条文（3）中的一般值控制。

若根据用地条件所能拟定的圆曲线最大半径R满足式（22），则根据式（5）、式（19）、式（20），并考虑条文（1）对缓和曲线最小长度的要求，联立以下不等式即可得出合理的Ls取值范围：

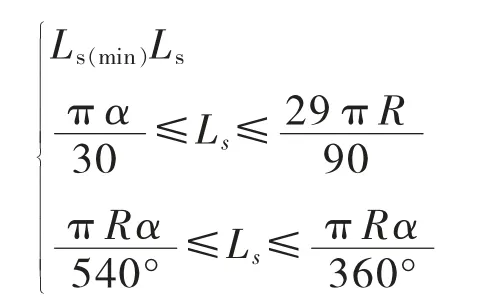
若R无法满足式（22），应对R是否满足式（23）进行验算。如果满足式（23），即，则平曲线长度按照条文（3）中极限值控制，应注意此时Ls＞LY，则必有β＞α/4≥3°，必然满足条文（2），且不具备满足第（5）条的条件，设计时缓和曲线长度Ls应按最小值Ls（min）选用，以保证尽可能长的圆曲线长度，此时平面线形方案应与降低设计速度、调整规划红线等其他方案进行比选。

如果R无法满足式（23），则必须采取降低设计速度、调整规划红线等措施。

5 结语

平曲线设计是城市道路工程设计中的重要内容，《规范》中对于平曲线设计提出了详细的要求，但由于规划红线的限制，城市道路平曲线往往不能自由调整，这就更加要求设计人员在设计过程中仔细推敲，参考《规范》时应结合实际建设条件，对相关条文灵活运用，从条文的基本原理出发，分析条文与工程的适应性，选取合理的设计指标，秉持“以人为本”的设计理念，力求在既定的设计条件下，确保道路行车安全，并尽可能提高行车舒适性、路线美观度，使工程效益最大化。