基于机载LiDAR数据提取建筑物顶面轮廓

陈 杰

( 中国能源建设集团江苏省电力设计院有限公司，江苏 南京 211102)

0 引言

LiDAR 是20 世纪90 年代开始投入使用的一种主动遥感观测系统，它通过激光传感器发射激光并且接收被物体反射后的回波，从而获取高精度的地面三维坐标，这种技术是对传统遥感手段的有效补充。

由于机载LiDAR 获取的数据为涵盖地面和地物的大量不规则分布三维点云，因此如何从这些点云数据中分别过滤出地面点和地物点已经成为近年来机载LiDAR 数据处理的研究主题，这项工作也是生成DTM 和DSM 以及城市三维重建工作的重要基础。

传统的建筑物提取和重建主要依靠摄影测量学技术，从立体像对中提取建筑物的相关信息[1]。而如今随着遥感观测技术的发展，建筑物提取和重建的主要数据源已经包括航空影像、高分辨率卫星影像[2]和机载LiDAR 数据等。其中，机载LiDAR 技术不仅能够检测房屋与它的轮廓，还能够提取屋顶表面信息，因此机载LiDAR 技术已经成为建筑物提取与重建的重要手段，如何从LiDAR 数据或者与其他数据的融合中提取与重建建筑物已经成为许多人研究的内容。

1 机载LiDAR数据过滤与分类

1.1 基于不规则三角网的LiDAR数据滤波方法

Vosselman[3]提出了一种基于斜率的方法来过滤非地面点，这种方法是一种改进的形态学腐蚀算法。一个点与其相邻点组成的向量斜率不大于阈值时，即认为这个点是地面点。Sithole[4]对这种方法进行了改进，根据局部地形特征运用不同的斜率阈值，因此需要粗略的坡度图来计算局部的斜率阈值。Rottensteiner[5]等利用DSM 和DTM 的插值(NDSM)和形态学开算子和尺寸窗口检测房屋和树木。

本文采用基于形态学和空间信息的LiDAR数据分层分类方法，将点云分类分为2 个步骤：滤波和目标分类。①将点云数据分成地面点和非地面点；②将非地面点进一步分成房屋点、植被点、车辆等。在对非地面点的分类中，采用了基于Axelsson[6]的改进的不规则三角网加密方法。首先由最小邻近区域算法获取初始的稀疏不规则三角格网，将满足设定的阈值条件的点添加到三角网中。然后，重新构建新的不规则三角网，并重新计算新的阈值。这样不断重复直到不再有新点加入为止。

添加新点的规则是把目标点到不规则三角网中相应三角形顶点角度，以及目标点到三角形面的距离与相应的阈值进行比较，如图1 所示。

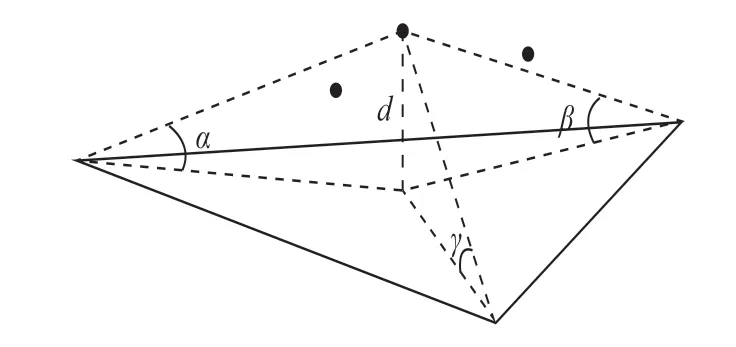
图1 不规则三角网添加新地面点示意图

阈值的选择在数据过滤中尤为重要，关系到每次能否找到正确的新地面点。其选择过程为：计算不规则三角网中各三角形内角以及各条边的边长，统计所有内角大小和边长值，通过直方图来确定角度阈值和边长阈值的大小，每次添加新点后都要重新计算角度阈值和边长阈值。

1.2 基于形态学的建筑物点提取

Meng[7]等提出了基于形态学的建筑物提取方法，首先应用滤波去除地面点，然后通过大小、形状、高度、建筑物结构和首次回波与末次回波之差等信息运用形态学的方法去除非建筑物的点。Hofmann[8]基于LiDAR 构成Delaunay 三角网提取建筑物屋顶，Karsli[9]等采用多次霍夫变换检测建筑物信息。

文中采用高程信息与形态学相结合的方法提取建筑物：首先根据非地面点在地面模型以上的高度值来区分点的类别。根据高程值将这些点分为低矮植被和高植被(比如树和房屋)。比如设定高度阈值为0.5 m，在地面点建立的三角形模型上比较目标点到模型的距离，如果低于0.5 m，就将这个点归到低矮植被的分类中。

从高植被点云中提取建筑物一般比较复杂，由于树木等高植被在高程上和建筑物相似，因此，仅依靠高程信息很难将建筑物准确提取。但建筑物和其他地物具有不同的几何分布：建筑物表面较为平整、高程变化小、而其他地物比如树木、电线杆等没有规则的几何形状，边缘高程变化较大。因此利用了8 领域搜索方法，结合高程信息进行建筑物提取。基本思路是根据相邻建筑物点高程变化小，并且分布规则、面积大等特点。算法如下：

1)将高植被点云格网化，生成规则的点集；

2)从高植被点云除去面积小于阈值条件的簇群；

3)对于树木和建筑物毗邻的情况，对其进行平面拟合，运用8 领域搜索方法，计算领域内高程值的标准偏差，如果小于阈值条件，则该点为建筑点，反之则分为高植被点。

2 建筑物顶面轮廓提取

为了提取建筑物的顶面模型，必须从离散的LiDAR 点云中提取建筑物的顶面轮廓，建筑物的顶面轮廓在城市基础地理信息数据库更新、变化检测、目标识别等领域有着广泛的应用价值，是LiDAR 数据处理的一项重要内容。

目前，基于LiDAR 数据提取建筑物顶面轮廓的一般方法是生成DSM 栅格图像，运用数字图像分割算法对其进行分割，然后用扫描线法、领域搜索法等方法实现建筑物顶面轮廓的提取，但这些方法提取的只是离散点集的粗略点集。

直接对离散点云提取轮廓的方法比较少，如Grahan[10]提出格雷汉姆算法来提取平面凸包轮廓，Edelsbrunner[11]提出了Alpha-shapes 算法并被沈蔚[12]等应用于提取离散点集的边界。

本文运用了基于Delaunay 三角网的建筑物顶面轮廓提取方法：①首先，将离散点云投影到XOY平面，生成Delaunay 三角网；②然后剔除边长大于阈值条件的三角形；③最后提取出只在一个三角形中的边作为离散点云的初始边界。

由于LiDAR 点云在空间分布的不规则性，提取的建筑物顶面轮廓十分粗糙，一般呈锯齿状，但现实中建筑物的顶面轮廓基本是光滑的。因此，还要进一步对轮廓进行规则化，而且由于大多数建筑物的相邻轮廓线满足直角约束条件，本文的建筑物顶面轮廓规则化方法如下。

2.1 基于Sleeve Algorithm的转折点提取

Sleeve Algorithm 由 Ma Ruijin[13]改进用于房屋轮廓的简化，sleeve 算法的优势在于它能够依次的处理点序列，这对于简化房屋轮廓十分合适。它的基本思路是用一根直径为d的管子来对应房屋轮廓点序列。如图2 所示为sleeve算法的原理图。

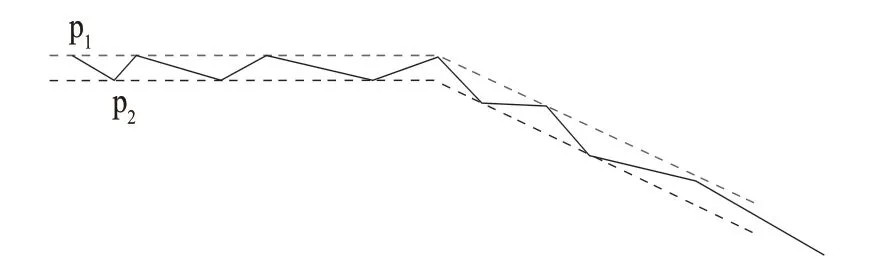
图2 sleeve算法的原理

由于管子的直径d是sleeve 算法唯一的参数，作为阈值判断边线上点偏离某一条线段的距离，从而决定该点是否为关键点(转折点)。本文中在实验中将对阈值d对结果的影响进行讨论。

2.2 基于主方向的转折点提取

建筑物的主方向是建筑物的重要特征之一。常见的计算建筑物主方向方法有：基于主成份分析的方法(陆见微[14])，基于Hough 变换的方法(杨化超[15]等)等。本文采用基于最小方向差拟合的主方向计算方法，它的原理如下。

1)用两条垂直的直线代表主副方向，称之为主(l)和副(l')方向线。αl和αl'为主副方向线的方位角，其中αl' =αl+90°，0°≤αl＜90°。

2)每条轮廓边的方位角为αi，则每条主副方向线的角度差定义为Di定义为：

3)将αl从0°取值到90°，计算每一次各条轮廓边与主副方向差之和∑Di。

4)取∑Di最小时对应的αl为主方向。

基于最小方向差拟合的主方向提取原理如图3 所示。

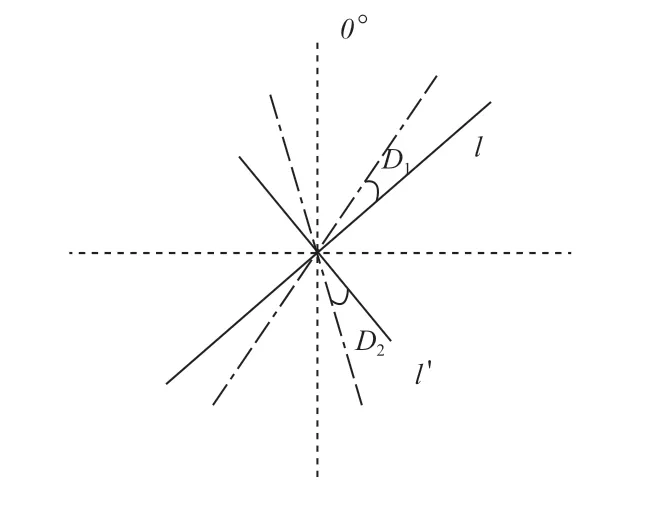
图3 最小方向差拟合提取建筑物主方向

2.3 轮廓规则化

由于现实中大多数房屋都有规则的形状，本文的轮廓规则化基于轮廓线相互垂直或者平行的假设，文中提出基于附加参数间接平差的轮廓规则化方法。

1)根据前文中提取的转折点将轮廓边分类。

2)将每一类的轮廓边的方位角加权求平均，权为该条边的长度li。

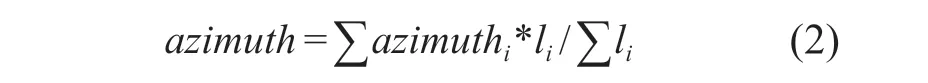
3)计算每一类的中心点的坐标，为每条边的中心点坐标加权求和。

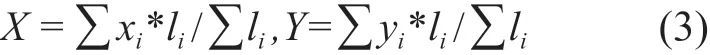
3 实验与分析

3.1 实验数据来源

本文数据由“黑河生态水文遥感实验(HiWATER)”产生，为2012 年覆盖甘肃黑河流域中游核心试验区的机载LiDAR 数据、2011 年无人机航摄影像数据[16]以及2012 年采集的该区域房屋角点、道路交叉点等控制点坐标，其中机载LiDAR 数据平均密度为4 点/m2，无人机航摄影像的空间分辨率为0.45 m。图4 中为同一区域的无人机影像和机载LiDAR数据。

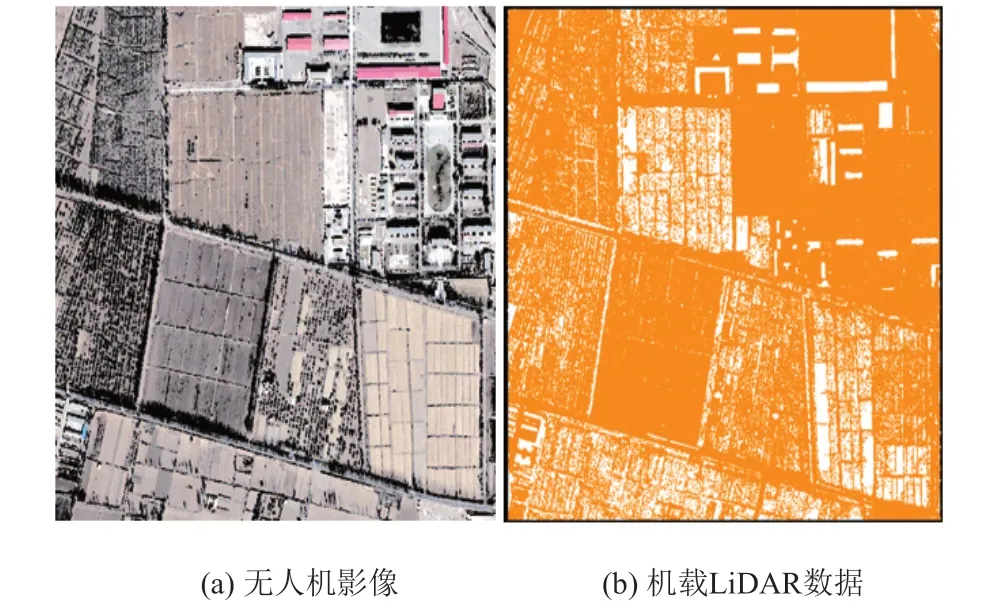
图4 无人机影像和机载LiDAR数据

3.2 机载LiDAR数据的滤波与建筑物提取实验

运用前文中所说的基于不规则三角网的点云滤波方法结果如图5 所示，左图中白色的为提取的地面点，黑色区域表示该处没有地面点，右图为利用滤波结果在商业软件中生成的DTM，其颜色表示点的高程，结合航空影像可以看出，结果对于植被、建筑点都能够较好的过滤。

图5 基于不规则三角网提取的地面点云

过滤出地面点与非地面点之后，采用了形态学的方法对非地面点先进行高程上的区分，区分出低矮植物，然后用8 领域搜索的方法，对于高植被和建筑物进行了区分，如图6 所示为最终的分类效果图，对照航空影像可以看出，结果对于建筑物的提取效果较为理想。

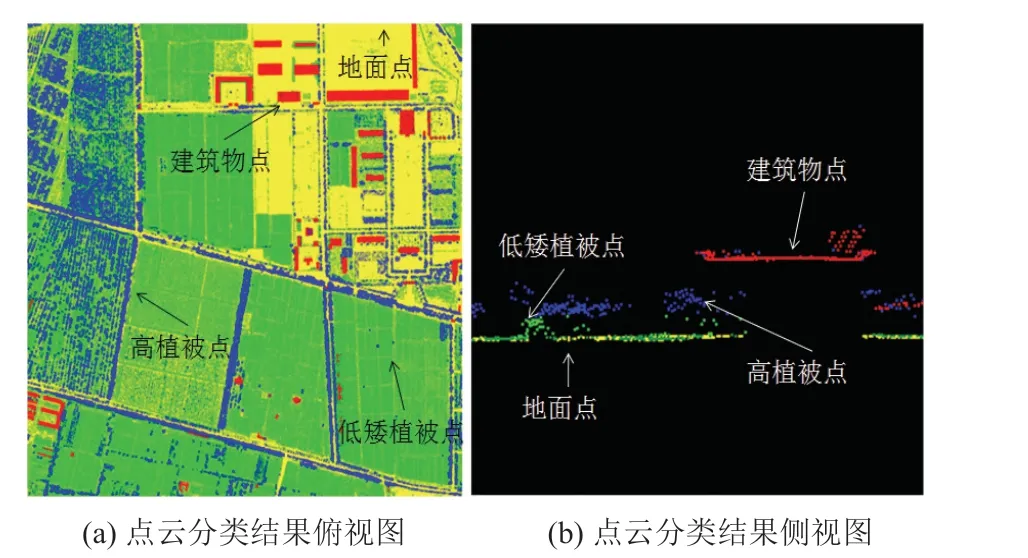
图6 基于8领域搜索的建筑物提取结果

3.3 建筑物顶面模型提取实验

3.3.1 建筑物顶面轮廓提取实验

提取出建筑物点云后，本文用商用软件裁剪出一幢建筑物的点云进行轮廓提取的实验，如图7 所示，所选房屋为普通的矩形房屋，(a)为生成初始三角网后以阈值为1 m 剔除大于阈值的边长所在三角形后的结果，(b)和(c)分别为阈值选择2 m 和3 m 的效果图，其中颜色较浅为保留的三角形，较深的为剔除的三角形。可以看出，随着阈值的增加，三角网的边缘逐渐平滑，但是细节逐渐丢失，因此本文选择了阈值为3 m 处理后的三角网。得到三角网后对其中仅在一个三角形中的边进行提取，将其作为建筑物轮廓的初始轮廓，图(d)即为提取的建筑物初始轮廓。

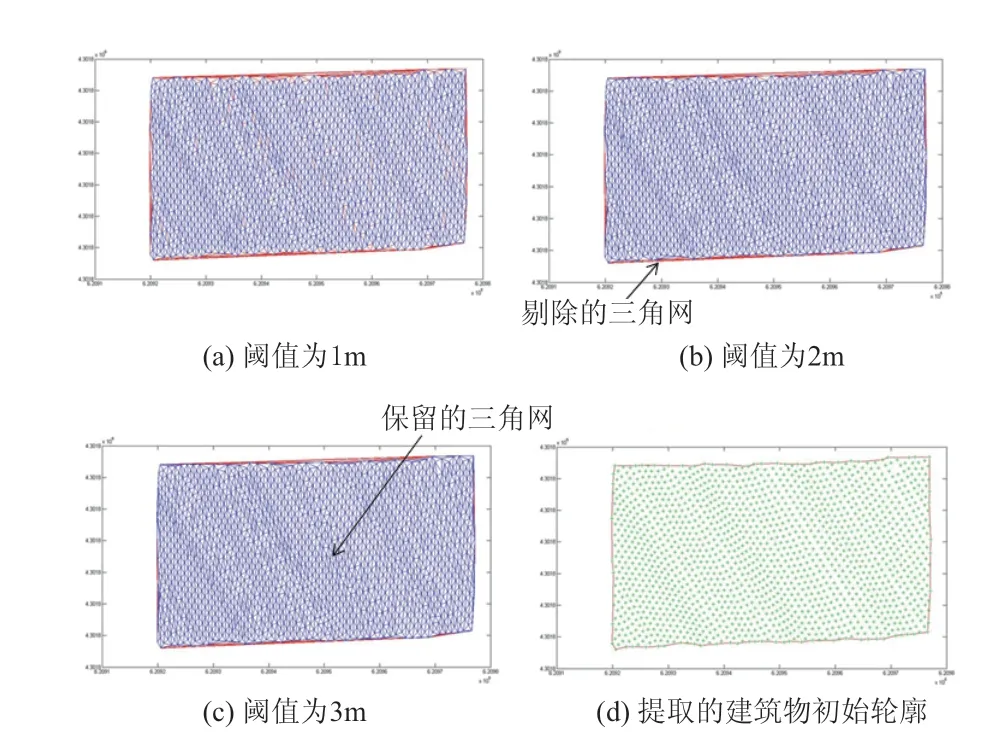
图7 去除边长大于阈值后的三角网

3.3.2 建筑物折点提取实验

提取建筑物顶面初始轮廓后，就获取轮廓点的坐标序列，由于初始轮廓凹凸不平，呈锯齿状，文中运用sleeve 算法和主方向法分别对初始轮廓提取转折点。sleeve 算法结果如图8所示。

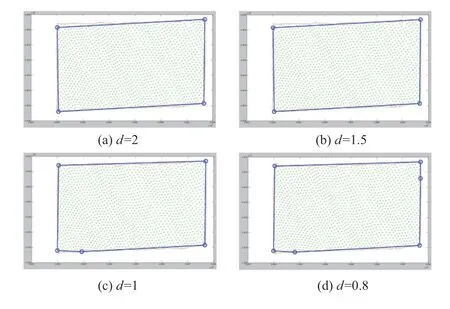
图8 sleeve算法结果

从图中可以看出，(a)结果与(b)没有变化，但当d=1时，sleeve得出的转折点由4个变成5个，d=0.8 时，转折点数为6，证明当d不断减小时，更多的点被当作转折点而被sleeve 算法所检测。实验证明d取1.5 比较合适。

文中除了sleeve 算法，也用基于最小方向差拟合的主方向判别法来对初始轮廓分类提取转折点，实验结果得出这幢建筑物的主方向方位角为1.570 8，根据该主方向将初始轮廓边分为两类：平行于主方向与垂直于主方向。实验结果如图9 所示。

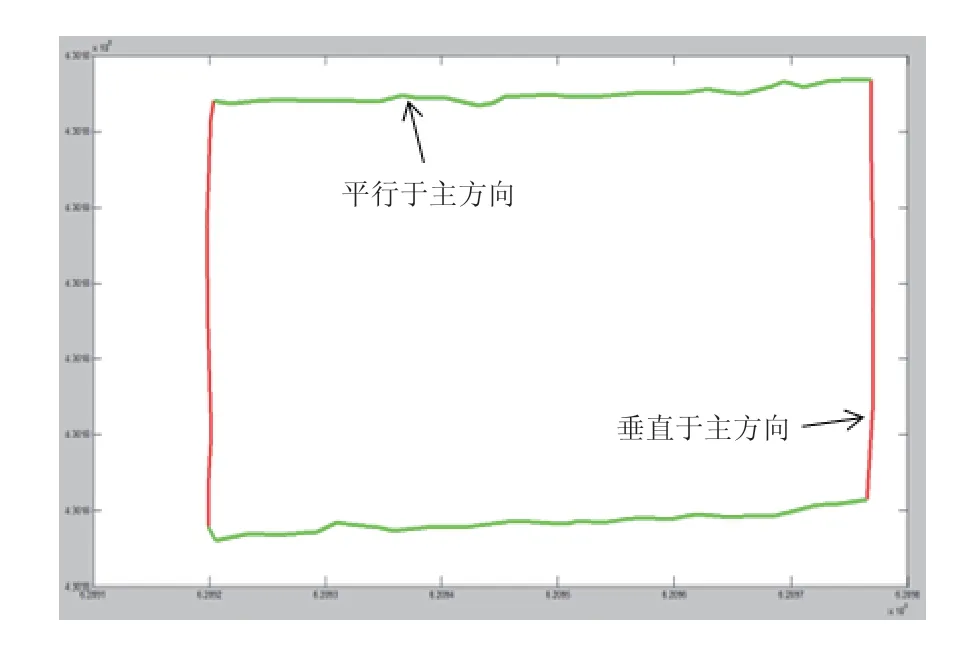
图9 基于最小方向差拟合的主方向判别

将sleeve 算法和主方向判别法的结果进行对比，主方向判别法在左上角的转折点判别中结果更为准确。

3.3.3 建筑物顶面轮廓规则化

根据上文的分类结果，文中运用基于附加参数间接平差对每一类的方位角进行了最优化，优化结果以及每一类的平均中点坐标如表1所示。

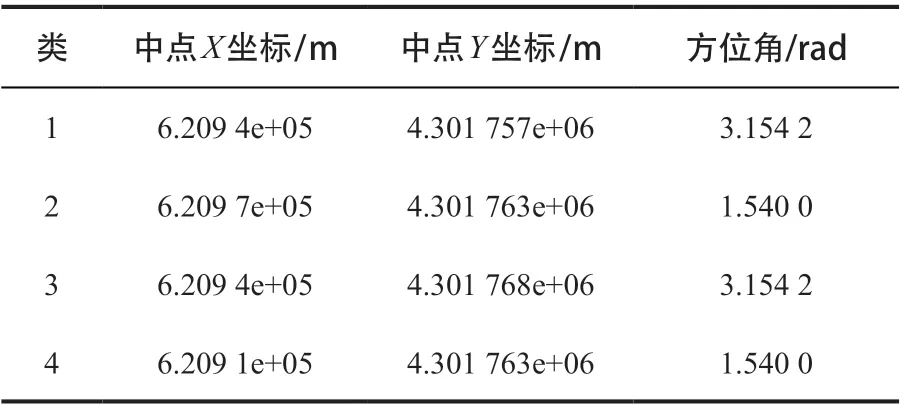
表1 轮廓规则化参数结果

图10 直观表示了规则化后的轮廓与初始轮廓的对比。

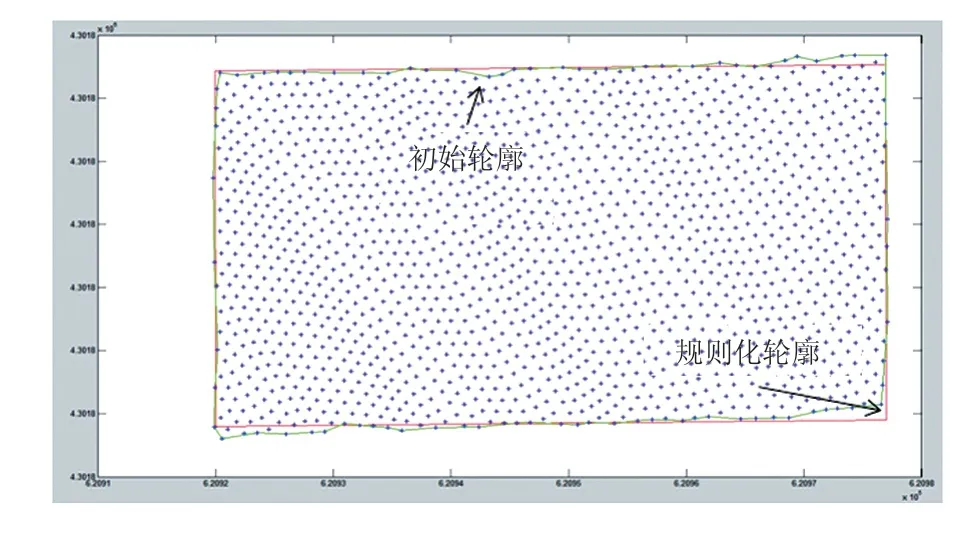
图10 规则化的建筑物顶面轮廓

为了对本文的建筑物顶面轮廓提取方法进行评价，在实验区域选择了4 个为建筑物顶面角点的控制点，它们分布在3 个不同的建筑物上，分别对其机载LiDAR 数据提取建筑物顶面轮廓,利用控制点坐标与提取的轮廓角点坐标进行对比，计算其残差和均方根误差(root mean squared error，RMSE)，结果如表2 所示。

表2 提取的建筑物顶面轮廓角点精度评价

结果表明提取的建筑物顶面轮廓角点X和Y方向的中误差均小于0.3 m,证明本文的方法能够较为精确地从机载LiDAR 点云数据中提取建筑物顶面轮廓。

4 结语

本文运用了基于不规则三角网和形态学的方法从机载LiDAR 数据中提取建筑物点云，然后用delaunay 三角网获取建筑物的初始轮廓，接着比较了sleeve 算法和主方向判别法对于初始轮廓分类的效果，最后提出附加参数的间接平差对于建筑物顶面轮廓的规则化，并获取了较高精度的建筑物顶面轮廓。

由于本文对于建筑物顶面轮廓的规则化基于其相互平行与垂直的假设，因此具有一定的局限性，如何高精度地提取不符合该条件的建筑物顶面轮廓需要做进一步的研究，另外提取的建筑物轮廓可以作为控制信息来提高其他异源数据比如航空影像、卫星影像的定位精度，这都是作者要进一步研究的内容。