异步电机直接转矩控制的仿真与研究*

王发良 ， 刘邦雄 ， 梅立雪

（景德镇学院机械电子工程学院，江西 景德镇 333000）

直接转矩控制技术是20世纪80年代兴起的一种新型电机控制技术，直接在定子坐标系下对电机电磁转矩进行控制[1]。基于定子磁链定向，采用离散的两点式滞环控制器产生PWM信号，直接对逆变器开关期间的状态进行控制，因而响应速度快。

相比较于矢量控制，直接转矩控制省去了矢量解耦控制，控制简单，便于理解。但是传统的直接转矩控制由于采用了两点式的滞环控制器对电磁转矩进行控制，造成控制系统的转矩脉动[2]。针对此问题，课题组利用零矢量具有保持转矩的特性，在传统的两点式滞环转矩控制器中加入零矢量，构成三点式滞环控制器，从而有效减小了转矩波动。

1 异步电机直接转矩控制原理

异步电动机电磁转矩表达式为[3]：

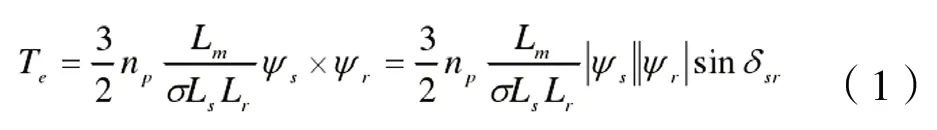
图1 异步电机直接转矩控制原理图

异步电机直接转矩控制是一个双闭环控制系统，外环的转矩调节控制器一般采用PI控制，内环采用转矩滞环、磁链滞环控制，其基本工作原理如下：给定转速和实际测量转矩的误差通过转矩调节器生成转矩给定，转矩给定和转矩模型估算出的转矩的误差通过转矩滞环比较器，生成转矩偏差信号TQ；同理，磁链给定和磁链模型估算出的磁链的误差通过磁链滞环比较器，生成磁链偏差信号ΨQ；最后，根据转矩偏差信号TQ、磁链偏差信号ΨQ以及定子磁链所属扇区θ选择合适的电压空间矢量，对逆变器进行控制，达到控制异步电机电磁转矩的目的。

1.1 磁链观测模型

利用传感器测量得到的定子电压、定子电流和转速等信息，能够对定子磁链的幅值和相位进行实时估计[4]。电压电流（U-I）模型方程是最常用的定子磁链观测模型。

1.2 磁链控制

磁链控制采用的两点式的滞环比较器，当给定信号和反馈信号之间的误差超出误差下限时，要减小磁链幅值，此时输出ΨQ为0；当给定信号和反馈信号之间的误差超出误差上限时，要增大磁链幅值，此时输出ΨQ为1；当给定信号和反馈信号之间的误差在允许范围内，不进行控制。如图2所示。

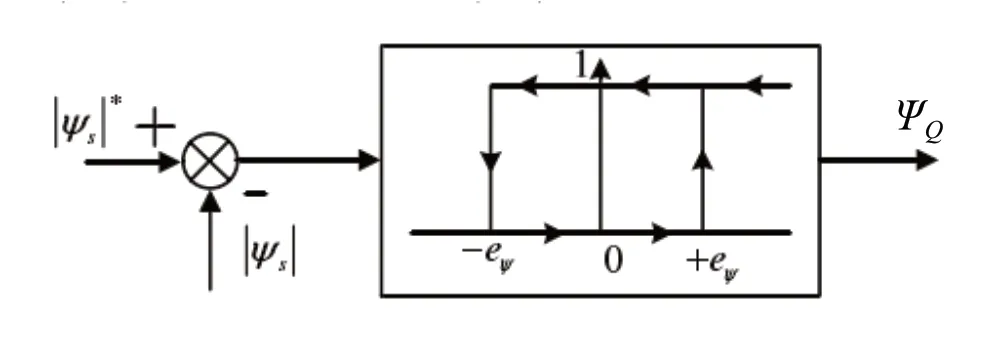
图2 两点式磁链滞环比较器

1.3 转矩观测模型

根据式（1），可以得到静止两相坐标系下电磁转矩观测器的表达式：

1.4 转矩控制

传统的转矩控制和磁链控制一样，采用的也是两点式的滞环比较器，但当转矩给定和转矩反馈之间的误差在允许范围内，转矩不受控会引起转矩波动[5]。针对此问题，本课题组采用三点式的滞环比较器，当转矩给定和转矩反馈之间的误差超出上限和下限时，其操作和两点式一样，唯一不同之处在于，当转矩给定和转矩反馈之间的误差在允许范围内，利用零矢量具有保持电磁转矩的作用的特性，引入了电压零矢量，从而减小转矩脉动[6]。如图3所示。

图3 三点式转矩滞环比较器

1）给定转矩值和测量转矩值的误差小于误差下限时，要减小电磁转矩，此时输出TQ=-1；

2）给定转矩值和测量转矩值的误差在允许范围内时，电磁转矩要保持不变，此时输出TQ=0；

3）给定转矩值和测量转矩值的误差大于误差上限时，要增加电磁转矩，此时输出TQ=1。

1.5 扇区判断

扇区划分方法如下：

基于αβ坐标系下的扇区划分图如图4所示。

图4 扇区划分图

1.6 定子电压空间矢量开关表

确定了转矩偏差信号TQ、磁链偏差信号ΨQ以及定子磁链所属扇区θ，就可以选择合适的电压空间矢量。经过分析可得到如表1、表2所示两种开关表。

表1 开关表（未加入零矢量）

表2 开关表（加入零矢量）

2 仿真分析

在Matlab2018b中的simulink下建立如图5所示加入零矢量的异步电机DTC仿真模型，电机基本参数如下：Pn=4 kW，Un=220 V，极对数为2，定子电阻Rs=1.45 Ω。

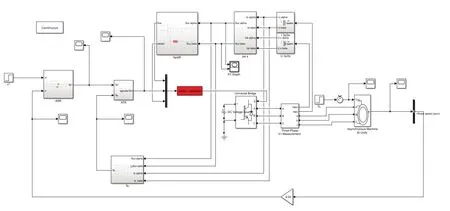
图5 加入零矢量的直接转矩控制仿真模型

仿真设置：给定转速800 r/min，给定磁链1 Wb，0.1 s加载50 nm，0.15 s减载50 nm。传统DTC和加入零矢量的直接转矩控制的磁链、转速和转矩的仿真结果分别如图6和图7所示。

图6 传统DTC算法

图7 加入零矢量的DTC算法

对比图6和图7，可以得到以下结论：1）零矢量的加入，不影响定子磁链；2）零矢量的加入使得转速超调更小；3）加入零矢量的DTC相比于传统的DTC，转矩波动明显减小。

3 结论

直接转矩控制由于其快速响应特性，广泛应用于异步电机控制领域，然而，传统的直接转矩控制存在转矩波动等问题，影响了其控制性能。利用零矢量具有保持转矩的特性，将其加入到异步电机转矩控制当中，仿真结果表明，零矢量的加入能够有效减小转矩波动。