超大直径盾构隧道机械法施工联络通道结构力学响应分析
2021-11-15刘明高马连友陆平张志陈仁东
刘明高 马连友 陆平 张志 陈仁东
1.北京市市政工程设计研究总院有限公司 100082
2.北京市首发高速公路建设管理有限责任公司 100166
3.北京交通大学土木建筑工程学院 100044
引言
双线盾构隧道间的横向联络通道是灾情发生时人员疏散和消防救援重要的生命通道。目前对于盾构隧道修建横通道,常规方法为对地层进行加固(冻结法、注浆法、旋喷桩法等),使其具有阻水性和自稳能力,而后拆除开口部位盾构管片,采用矿山法构筑横通道。但采用此类非机械法施工风险大,若加固效果不良,阻水及自立性不足,将会引发涌水坍塌等事故,后果非常严重[1]。而且此类方法工期长、冻结法施工工后融沉大、施工效果难控,因此国内外已对联络通道的机械法施工展开了探索[2,3],如德国汉堡易北河、香港屯门赤鱲角连接线、宁波地铁盾构隧道等。但对于超大直径盾构隧道机械法施工联络通道的结构受力及变形特征影响研究不足,因此本文依托北京东六环路改造工程盾构段横向联络通道工程实践,采用数值模拟的手段对不同工况下机械法施工荷载对主体结构的影响展开研究。
1 工程概况
北京东六环路(京哈高速~潞苑北大街)改造工程盾构段长7341m,盾构隧道管片外径达15.4m,为国内最大直径之一,盾构段设置有6条人行横通道,长度为15.7m~21.2m,埋深为27.2m~62.8m,水压0.17MPa~0.46MPa,主要位于细砂、粉质黏土层。本文主要针对其中7#横通道展开研究,埋深及地质情况如图1所示。
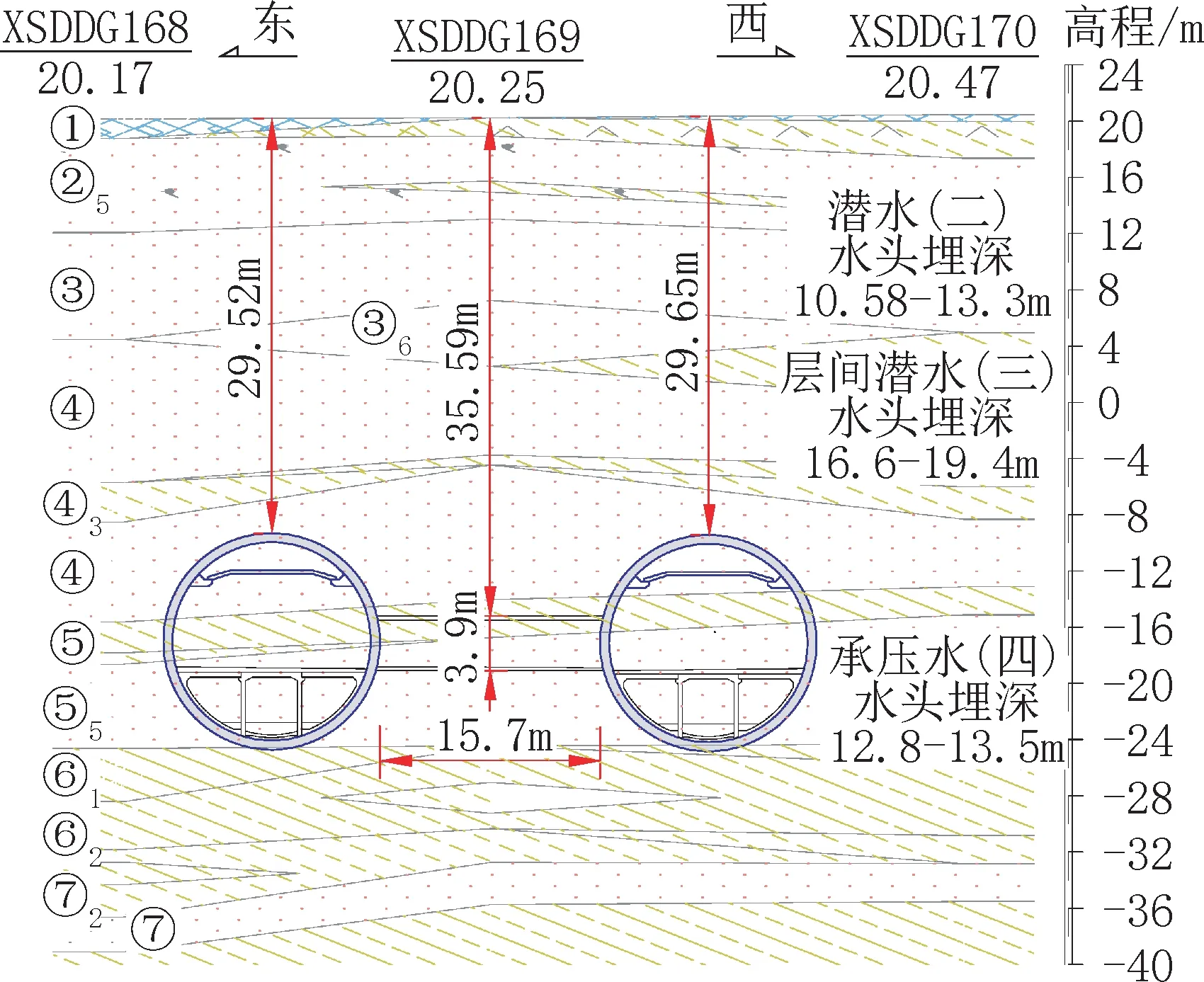
图1 7#横通道地质情况Fig.1 Geological conditions of7#cross-passage
2 数值模拟方案
本文采用ABAQUS软件建立三维模型,研究机械法联络通道施工过程(掘进机顶出主洞隧道后),施工荷载对主体结构受力及变形的影响。
2.1 地层参数
设计条件显示,主体盾构隧道拱顶埋深29.7m,双线盾构隧道净距(联络通道长度)为15.7m。为避免边界效应,盾构隧道两侧土体各取26.75m,横向长度为100m,沿盾构纵向取15环纵向长度为30m,土体总厚度为竖向取63.7m。因此模型尺寸为100m×63.7m×30m。地层土体本构选用ABAQUS内设的扩展Drucker-Prager本构模型,相比于常用的Mohr-Coulomb模型,具有计算效率高、收敛更容易等优点,且材料参数可从Mohr-Coulomb模型中进行换算,换算公式[4]为:
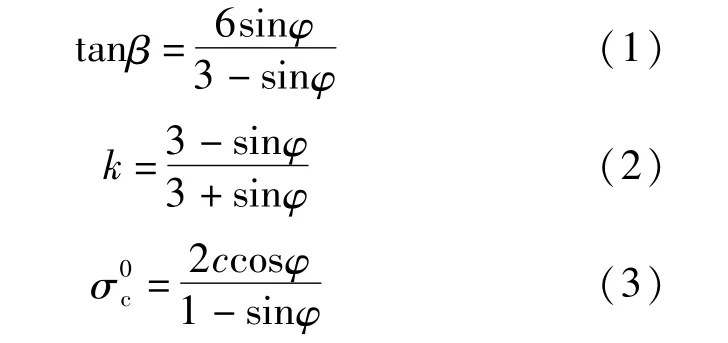
式中:c、φ分别为Mohr-Coulomb模型中的黏聚力(kPa)和内摩擦角(°);β、k、分别为Drucker-Prager模型中的内摩擦角(°)、流应变比、屈服应力(kPa)。三维模型如图2所示,土体参数见表1。
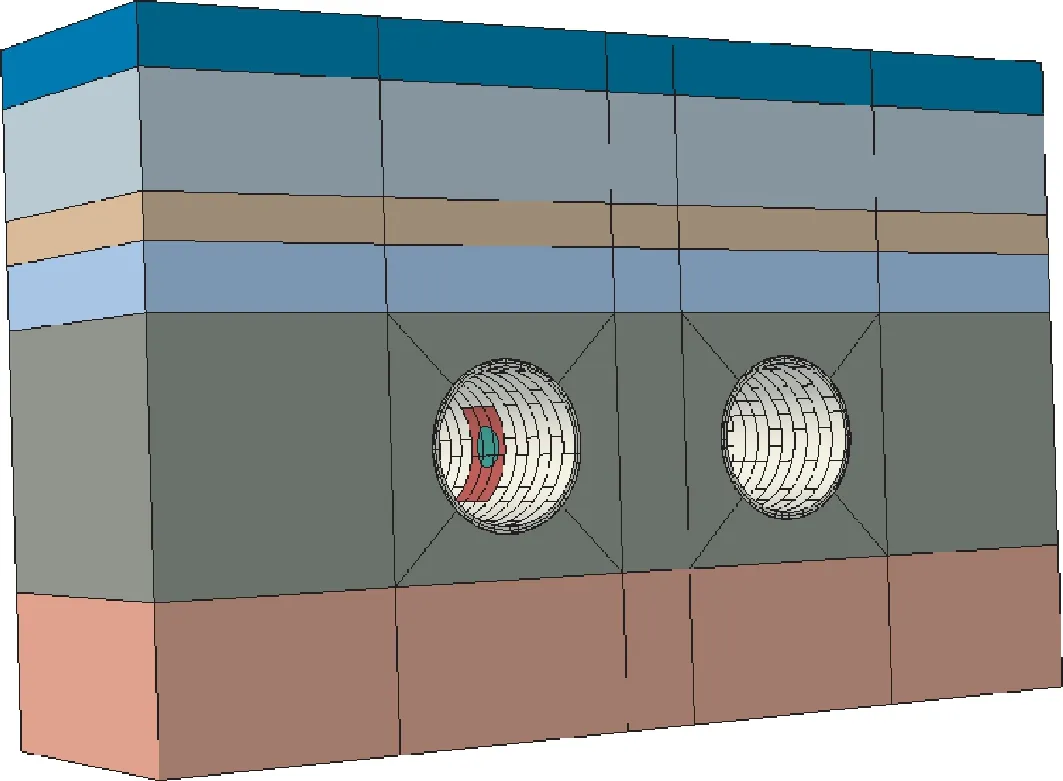
图2 三维数值模型Fig.2 Three-dimensional numerical model
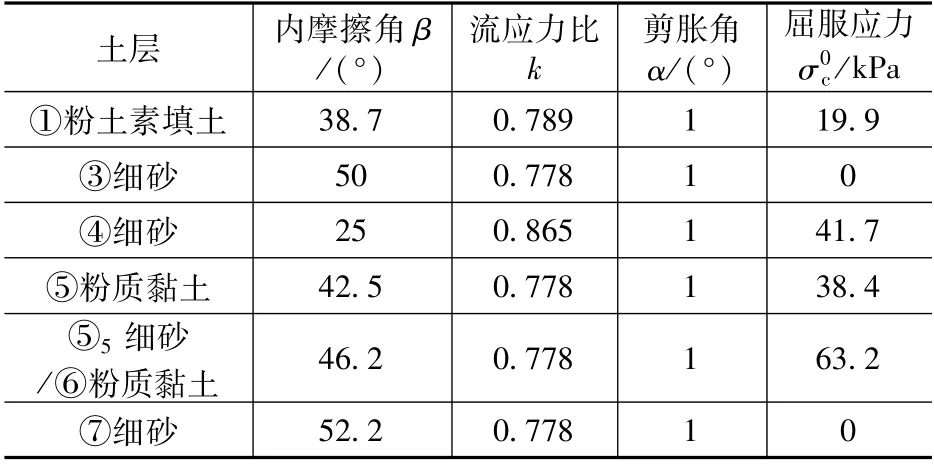
表1 土体参数Tab.1 Soil parameters
2.2 盾构隧道参数
盾构隧道的模型按照实际尺寸建立,隧道外径取15.4m,管片厚度取0.65m,环宽取2.0m(未考虑楔形量),每环采用10片管片,错缝拼装,盾构隧道管片采用C60混凝土。联络通道建筑限界宽2m×高2.5m,横通道为圆形,外径为3.9m,开口部位涉及3环共6块管片。参考国内外机械法横通道建设经验,将开口6块设计为复合管片。可切削部位设置为纤维筋混凝土C40,非可切削区为钢板-混凝土复合衬砌。管片结构均采用理想弹性本构模型,各材料参数见表2。
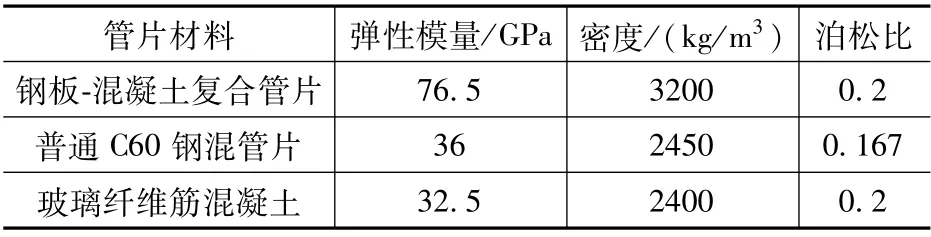
表2 管片参数Tab.2 Segment parameters
环内接头的抗弯由混凝土抗压和螺栓抗拉共同完成,管片为实体单元,设置为硬接触,可传递压应力,螺栓由抗拉弹簧模拟。环间接头的抗剪由接头摩擦力、分布式凹凸榫、斜螺栓等共同承担。已有研究表明[5],由于拼装误差,凹凸榫往往已存在搭接,且螺栓与螺栓孔间隙比凹凸榫间隙更小,因此环间抗剪主要由凹凸榫来承担。通过经典材料力学公式[6]计算环内接头的等效弹簧刚度为ks=2.84×108N/m(沿管片环向),环间接头的等效弹簧刚度为kst=3×109N/m(沿管片环间接触面的任意方向)。接头按照实际位置布置,环内弹簧每环沿纵向布置3个,环间弹簧沿环向布置28个。
2.3 施工荷载工况
考虑到本项目主隧道为超大直径盾构隧道,外径达到15.4m,所以施工荷载施加方式借鉴香港屯门赤鱲角项目施工案例,如图3所示。机械法掘进机顶推的反力由反力架传递到主体盾构隧道开口同侧的4个锚固端头(1.2m×1.2m)上,因此作用在主体结构上的施工荷载为作用在端头上的张拉力荷载。数值模拟荷载施加方式如图4所示。

图3 香港屯门隧道机械法施工联络通道案例Fig.3 Cross passage of Tuen Mun-Chek Lap Kok Link tunnel constructed by mechanical method
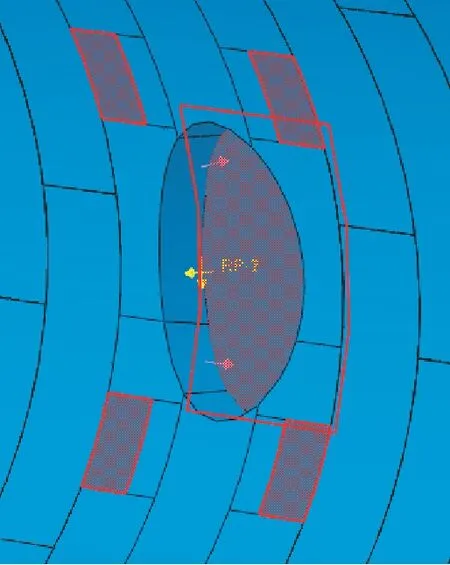
图4 拉力荷载作用区域Fig.4 Tensioning force loading area
机械法可以分为顶管法和盾构法,但两者反力的提供方式是相同的,且顶管法所需的顶推反力更大,因此本文的荷载选取顶管顶推力,并依托7#横通道工况对顶推力进行初步计算[7],公式如下:
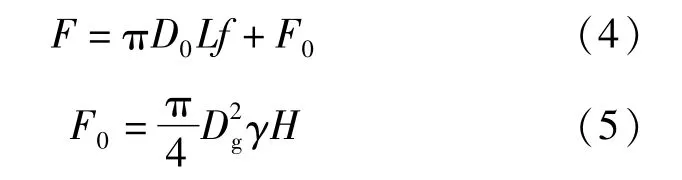
式中:F为总顶进力(kN);D0为管道外径(m),取3.9m;L为管道设计最大顶进长度(m),取15.9m;f为管道外壁与土之间的平均摩阻力(kN/m2),北京市经验取值为10kN/m2,若考虑土体浮重度为γ′=10kN/m3,考虑土拱效应埋深取2倍的顶管直径为8m,顶管机与周围土体的摩擦系数取0.4,计算得到平均摩阻力约为28kN/m2;F0为顶管机的迎面阻力;Dg为顶管掘进机外径(m),取4.0m;γ为顶管覆土的重度(kN/m3),加权平均取20kN/m3;H为顶管覆土深度(m),取埋深35.6m。
计算可得F0=8867kN,当摩阻力取28kN/m2,管节取最长值时,总顶推力的最大值为F=14460kN。综合以上,偏于安全考虑,设定模拟荷载范围为0~30000kN,取9个工况,分别为0kN、3000kN、6000kN、9000kN、12000kN、15000kN、20000kN、25000kN、30000kN。
3 数值模拟结果分析
3.1 位移分析
1.竖向位移
不同反拉力荷载工况下,主体结构的竖向位移云图如图5所示,限于篇幅只列出荷载为0kN、9000kN、20000kN、30000kN工况的模拟结果。由图5可知,不同荷载作用下,隧道整体变形模式一致:隧道顶部发生沉降,底部发生隆起,并随荷载的增大,沿隧道纵向有不均匀的趋势。提取各环顶部和底部位移值绘制曲线,如图6所示。可知,随反拉力荷载的增大,主体结构的顶部沉降和底部的隆起位移逐渐减小,即结构的竖向收敛值逐渐降低。对于开口环,相较于荷载为0的工况,荷载增加到30000kN时,主体结构顶部沉降减小了2.82mm(40.4%),底部隆起减小了1.99mm(7.9%),竖向收敛减小了4.81mm(14.9%)。
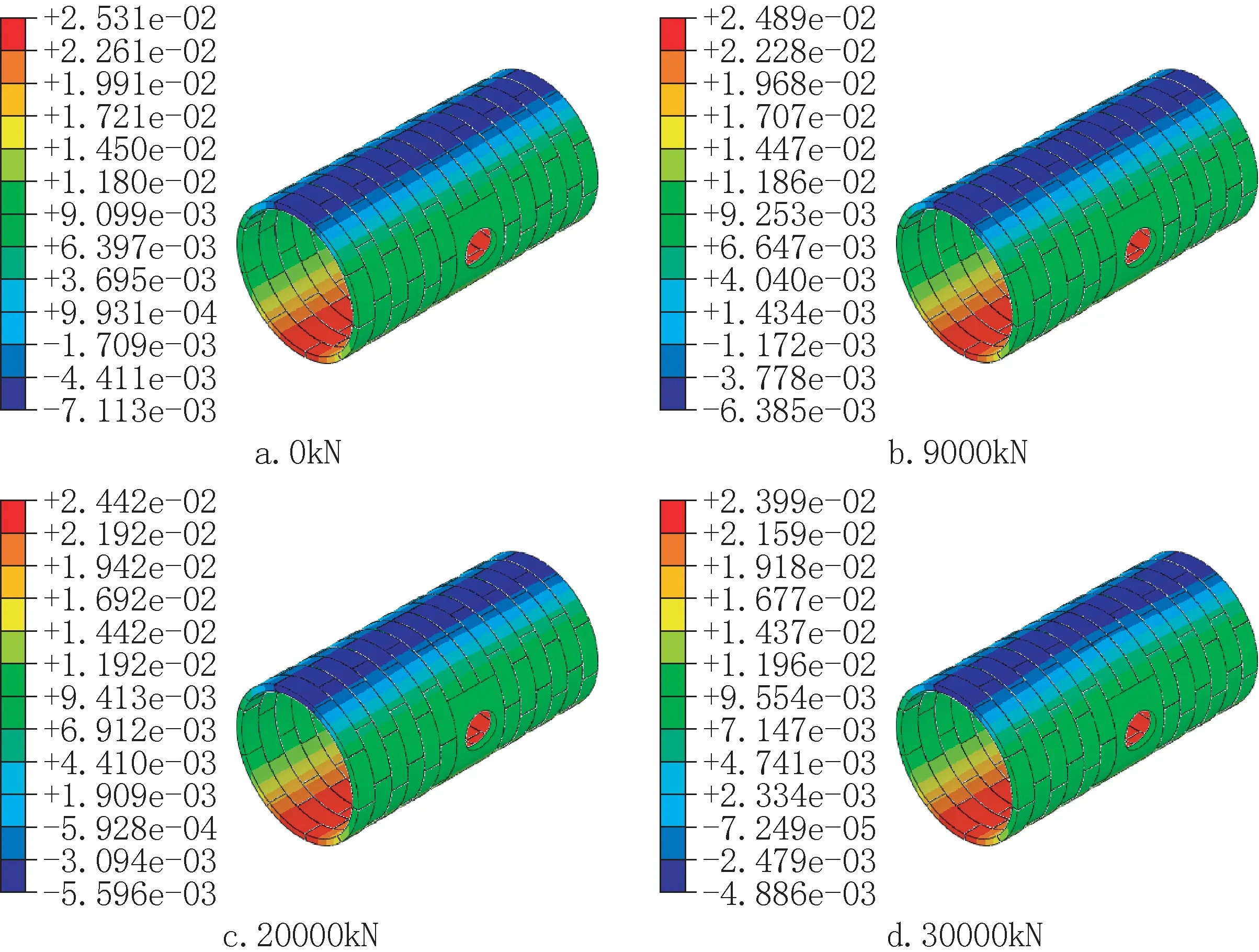
图5 不同荷载条件下主隧道竖向位移云图(单位:m)Fig.5 Vertical displacement contours of main tunnel under different load conditions(unit:m)
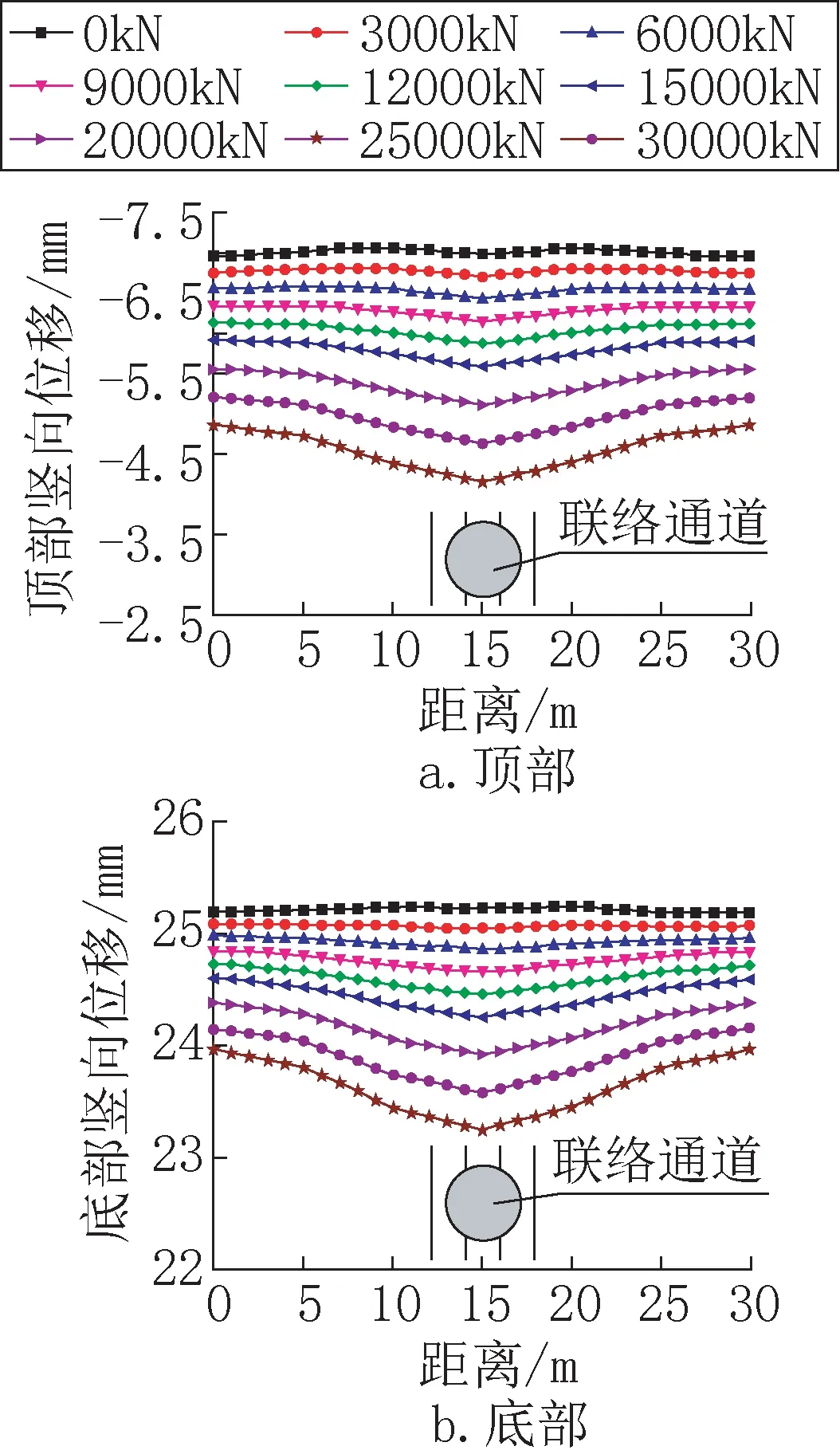
图6 盾构隧道竖向位移沿纵向变化情况Fig.6 Variation of vertical displacement of the shield tunnel along longitudinal direction
2.横向位移
不同反拉力工况下,主体结构的横向位移云图如图7所示(向右为正),限于篇幅只列出荷载为0kN、9000kN、20000kN、30000kN工况的模拟结果。由图7可知,不同荷载作用下,隧道整体变形模式一致:隧道左侧发生向左的位移,右侧发生向右的位移,并随荷载的增大,位移云图沿隧道纵向有不均匀的趋势。
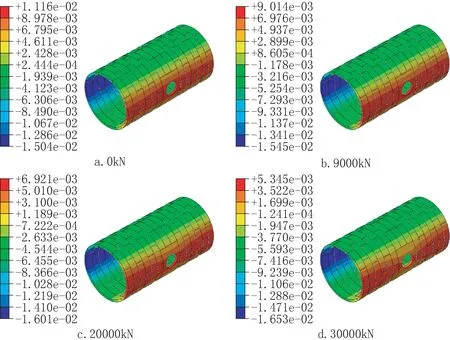
图7 不同荷载条件下主隧道横向位移云图(单位:m)Fig.7 Horizontal displacement contours of main tunnel under different load conditions(unit:m)
提取各环左侧和右侧的位移值绘制曲线如图8所示。分析左侧位移情况可知随反拉力荷载的增大,主体结构的左侧产生向左的位移,荷载为30000kN的工况,相较于0荷载工况,隧道左侧向左移动了1.41mm。

图8 盾构隧道横向位移沿纵向变化情况Fig.8 Variation of horizontal displacement of the shield tunnel along longitudinal direction
分析右侧位移可知,随反拉力荷载的增大,主体结构的右侧也产生向左的位移。荷载为30000kN的工况,相较于0荷载工况,隧道右侧向左移动了7.40mm。进一步分析隧道右侧的变形曲线可知,反拉力荷载小于15000kN时,主体结构开口环部位向右位移最大,说明由于开口环结构刚度的削弱,主体结构在开口部位向外挤出,椭圆度增大。当反拉力进一步增大到15000kN以上时,主体结构开口环向右的位移最小,说明由于拉力荷载的作用,抵消了由于开口环结构刚度削弱而产生的向外的挤出变形,结构的椭圆度减小。
3.结构椭圆度
绘制开口环结构的椭圆度随荷载的变化情况,如图9所示,可知不同荷载下主体结构椭圆度均满足规范要求(8‰),而且随荷载的增大,椭圆度近似呈线性减小,荷载30000kN的情况相比于0荷载情况,椭圆度减小了18.5%。
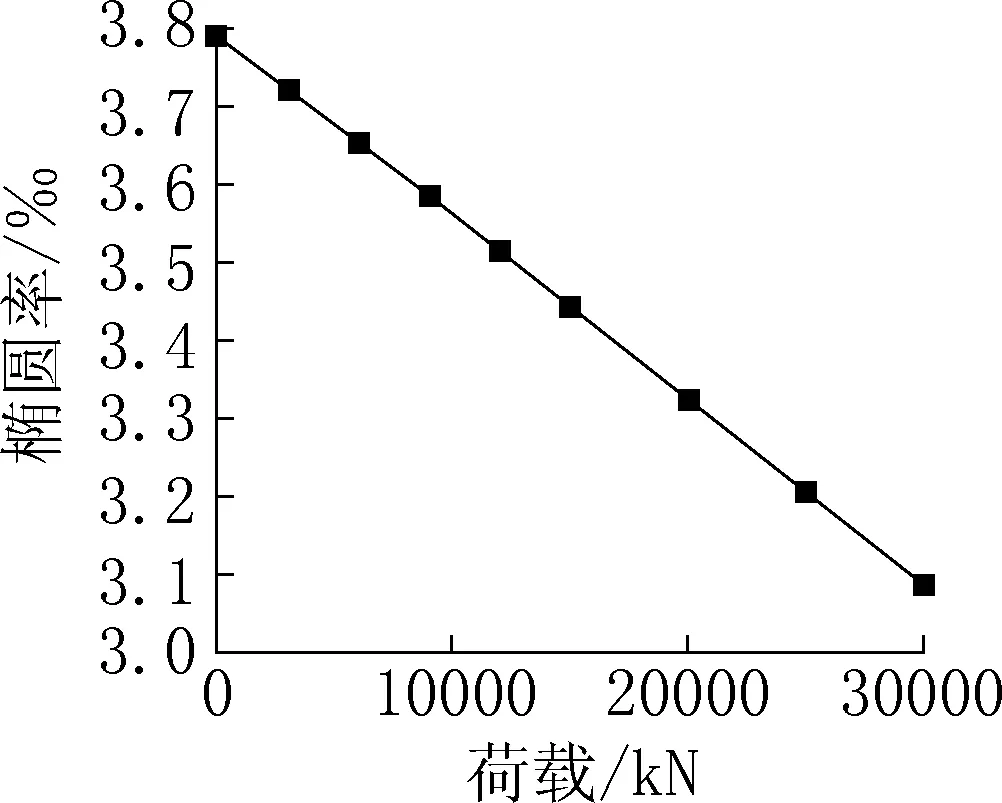
图9 开口环椭圆度随荷载变化情况Fig.9 Variation of ellipticity of opening ring with the load
3.2 最大主应力分析
在30000kN反拉力荷载作用下,主体隧道最大主应力云图如图10所示。可知,最大主应力主要集中在开口部位,其他部位受力较为均匀。提取9种工况下开口部位的主应力云图如图11。可知结构承受最大拉应力位置相同。且随着荷载的增大,结构应力云图分布形式发生变化,由开口部位四周的拉应力域逐渐变为锚固端附近的拉应力域。
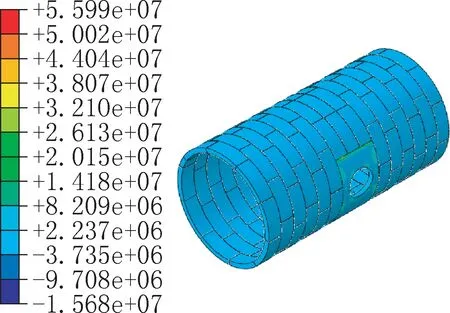
图10 30000kN工况下主隧道应力云图(单位:Pa)Fig.10 Stress contour of main tunnel under30000kN condition(unit:Pa)
提取图11中9种荷载工况下,主隧道管片最大拉应力和最大压应力,见表3,并绘制主体结构最大拉应力随荷载的变化曲线如图12所示。可知,随着施工荷载的增大,结构所受最大拉压应力也增大,荷载为30000kN工况相比于0荷载工况,拉应力增大4.87MPa(9.45%),压应力增大3.3MPa(26.66%),但也均在钢板复合管片的承载能力范围内(Q235钢板抗拉压刚度为225MPa),可保证结构的安全。
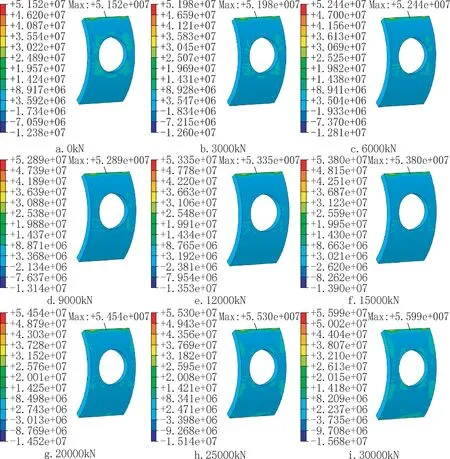
图11 不同荷载作用下结构最大主应力云图(单位:Pa)Fig.11 Maximum principal stress contours of main tunnel under different load conditions(unit:Pa)
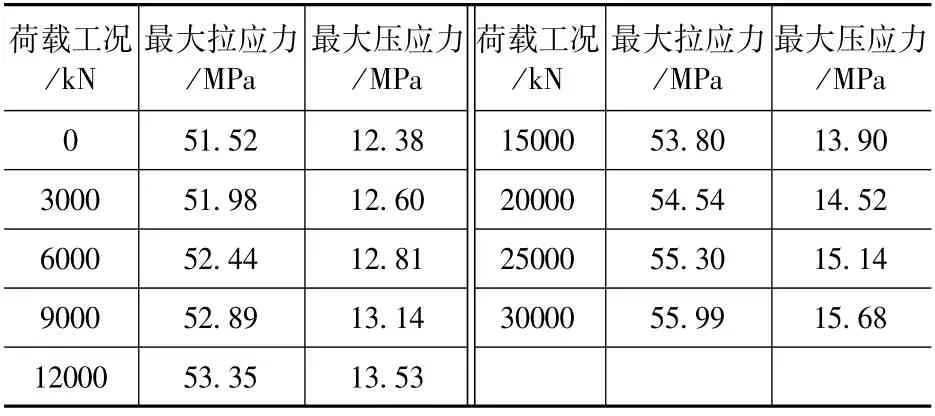
表3 不同荷载工况下主隧道最大主应力Tab.3 Maximum principal stress of main tunnel under different load conditions
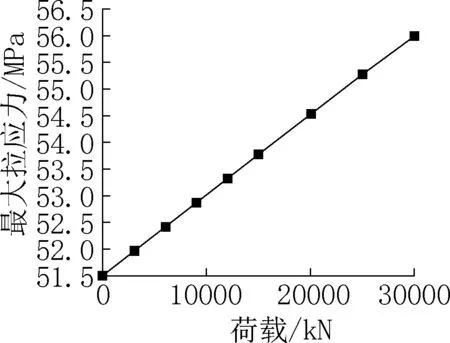
图12 不同荷载工况下开口部位最大拉应力Fig.12 Maximum tensile stress of the opening part under different load conditions
4 结论
1.随拉力荷载的增大,结构顶部沉降和底部隆起值均逐渐减小,荷载为30000kN工况相比于0kN工况,顶部沉降减小2.82mm(40.4%),底部隆起减小了1.99mm(7.9%),竖向收敛减小了4.81mm(14.9%)。
2.随拉力荷载的增大,结构整体向左(开口对侧)发生位移。荷载为30000kN工况相比于0kN工况,右侧向左位移了7.40mm,左侧向左位移了1.41mm。
3.开口环结构椭圆度随反拉力荷载的增大而呈线性减小的趋势,且结构椭圆度均满足规范要求。从变形与内力变化规律与趋势来看,采用“拉力型”反力对于主体结构受力是有利的。
4.随反拉力荷载的增大,结构所受最大拉应力和压应力均发生一定增大,荷载为30000kN时,结构所受最大拉应力为55.99MPa,但均在钢板复合管片的承载能力范围内,说明在施工过程中结构可保证安全。
