面向小学计算思维培养的项目式教学设计

吴莹颖

摘要：计算思维是信息技术学科重要的核心素养之一。如何高效开展小学生计算思维培养成为研究重点。本文以计算思维六大过程要素为切入点，结合项目式学习，探索面向学习者计算思维培养的项目式教学模型，并以“2022冬奥会宣传”为具体案例，通过“提出问题—分析问题—探究实践—讨论交流—评价展示”这一教学流程，提升学生的计算思维素养。

关键词：计算思维;可视化编程;项目式教学

中图分类号：G434  文献标识码：A  论文编号：1674-2117（2021）21-0046-04

计算思维是指“运用计算机科学的基础概念进行问题求解、系统设计，以及人类行为理解等一系列思维活动”，其包括六大过程要素：界定问题、抽象特征、建立模型、设计算法、实施算法、迁移应用。计算思维作为信息技术核心素养之一已成为小学信息技术教学的主要任务与目标之一。小学阶段学生的低认知水平与计算思维的高要求之间形成一对主要矛盾，如何高效开展小学生计算思维培养成为研究重点。

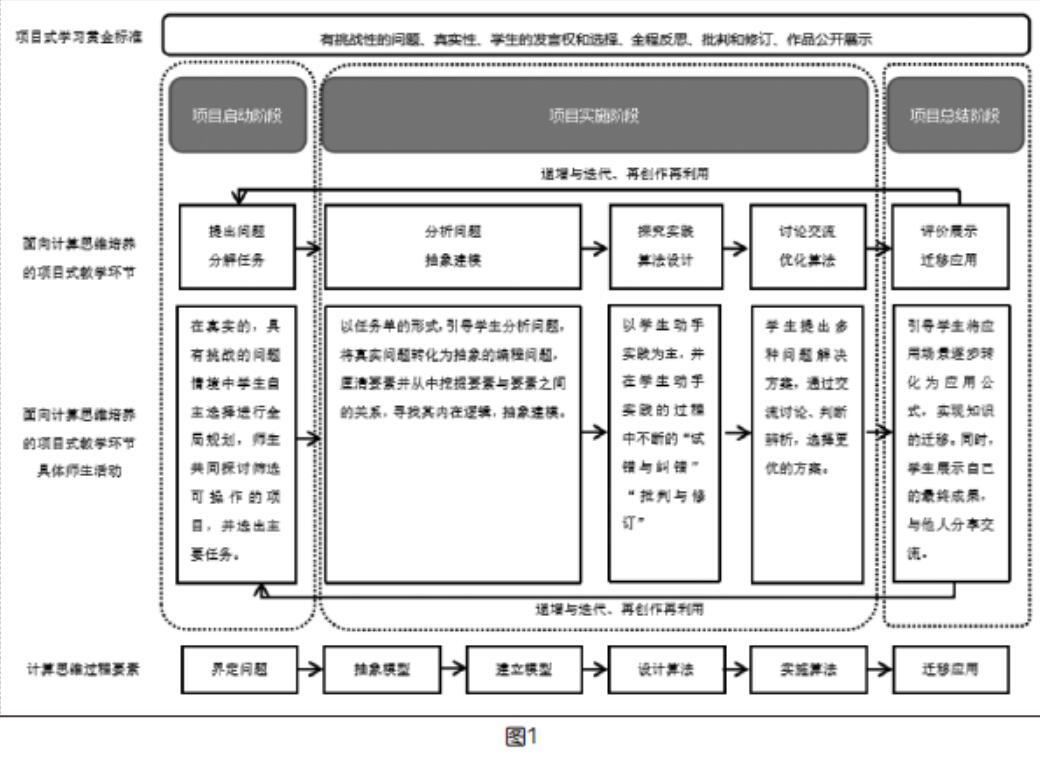
项目式学习（PBL）是以学习者为中心，学生围绕真实复杂的问题进行探究，并在主动探究的过程中积极建构新知，形成一定的成果，从而提高自身综合素质的一种教学模式。巴克教育研究所对项目式学习提出了“黄金标准”：富有挑战性的问题或困难、持续探究、真实性、学生的发言权和选择、全程反思、批判和修订、作品公开展示。项目式教学模式契合计算思维核心素养的培养，它能更好地帮助编程活动设计明晰起点与目标，从而提升学生的计算思维。因此，笔者以计算思维六大过程要素为切入点，结合项目式学习的特征与标准，构建了面向学习者计算思维培养的项目式教学模型（如上页图1），同时，基于可视化编程软件，以“2022冬奥会宣传”项目式教学设计为例，具体展示面向计算思维培养的项目式教学设计。

提出问题，分解任务

编程教学经常进入传统教学模式误区，以知识点教学为主。看似“有序”的知识点教学对于学生的知识建构而言恰恰是“无序”的，学生学习了基础的计算概念，但是却很难将这些计算概念建立有效的关联，在后期的编程创作中，知识的迁移应用成了难点，同时学生的计算实践以及计算观念也很难得到发展。而在较大的项目情境学习时，学生将不断地与问题情境产生互动，在已有经验与新问题之间不断建立关联，创设意义，建构知识体系。同时，较大的项目式学习将给予学生更充分的实践时间，更有利于学生的深度学习。

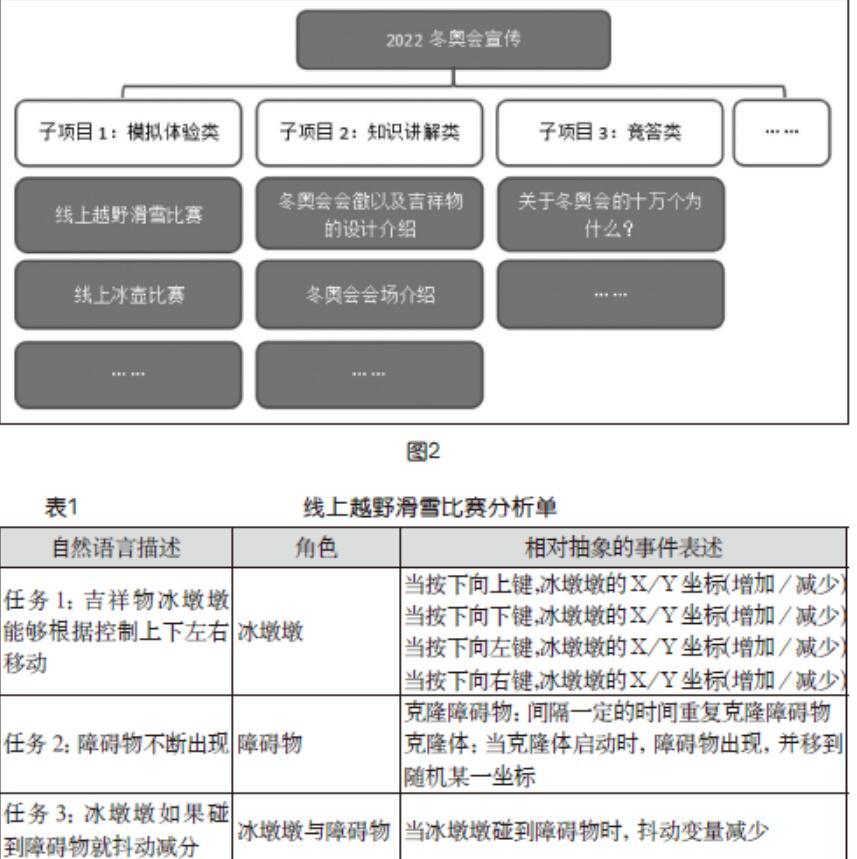
以“2022冬奥会宣传”这一项目学习为例，教师通过展示一段冬奥会的视频，创设问题情境：2022年冬奥会即将在我国北京举行，同学们能不能利用所学的可视化编程软件，宣传2022冬奥会。通过这样一个真实的劣构问题，激发学生展开头脑风暴。学生围绕着问题情境，搜索相关资料，开展小组讨论，对程序进行全局规划设计，提出了关于此问题的相关规划构思（如图2）。

教师引导学生在诸多想法中，寻找可操作、可执行的设计想法，并将设计想法进行有效的识别归类、筛选形成可执行的设计方案。通过这样的头脑风暴，能够引导学生更好地发散思维，不断丰富预设目标，扩充程序内容。在学生自行拟定的规划框架之上，师生共同探讨、筛选出主要任务“线上越野滑雪比赛”，并分析任务，化繁为简，将这一大任务分解成了三个小任务：吉祥物冰墩墩滑雪;障碍物不断出现;冰墩墩与障碍物。通过明确主要任务，分解任务，引导学生在接下来的项目学习过程中有的放矢。

分析问题，抽象建模

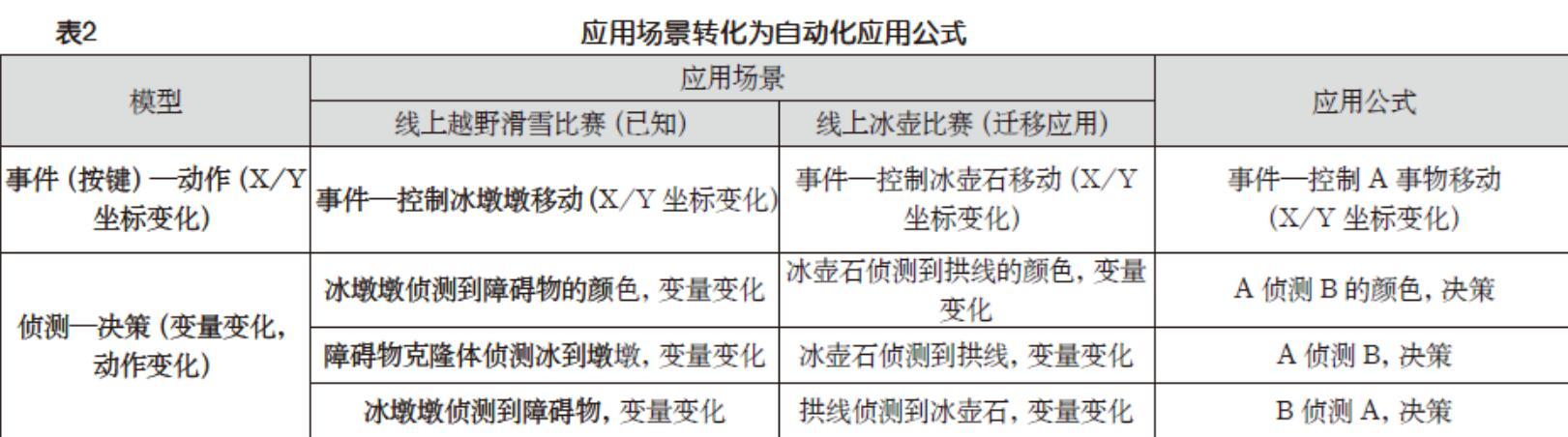
根据明确的主要任务，教师通过问题分析引导学生将真实问题转化为抽象的编程问题，厘清要素并从中挖掘要素与要素之间的关系，寻找内在逻辑。在这一任务中，教师通过任务单的形式，引导学生小组讨论，并填写相应的表格（如表1），将问题从自然语言的表述向积木搭建转化，从而将问题抽象化。例如，任务1学生的自然语言描述为“吉祥物冰墩墩能够根据控制上下左右移动”，而“上下左右移动”这一自然语言表述在计算机中是不可识别的，因此教师可引导学生转换为“X/Y坐标的增加与减少”，提炼出关键要素，建立初步模型：事件（按键）—动作（X/Y坐标变化）。任务2学生的自然语言描述为“障碍物不断出现”，在编程中如何实现障碍物的反复出现呢？教师通过引导使学生能够归纳分析出“克隆”这一关键词。任务3学生的自然语言描述为“冰墩墩如果碰到障碍物就抖动减分”。这时教师应注意引导学生将语言转换为“当冰墩墩碰到障碍物时，就抖动并且变量减少”。把减分转换为“变量的减少”，简化抽象模型：侦测—决策（变量变化，动作变化）。通过这样的引导转化，从具体向抽象逐步转化，提升了学生分析问题能力以及抽象能力，为后期的编程实践打下基础。

探究实践，算法设计

项目式学习最重要的环节是学生的主动探究实践，程序设计更离不开学生的探究实践，学生在反复试错的过程中不断反思，收获新知。例如，学生在根据“线上越野滑雪比赛”分析任务单进行自主编程时，会发现任务1中对冰墩墩套用“事件（按键）—动作（X/Y坐标变化）”模型之后，冰墩墩会移出屏幕且周围背景无变化。这时，教师根据学生在实践过程中遇到的问题，提出相对运动这个知识点，并播放动画《汽车与小树》。“当我们坐在汽车上看窗外的小树时，是不是觉得小树在移动，但实际上是车在运动，小树是静止的。如果我们是站在小树旁看汽车，这时的汽车是运动的而我们是静止的，所以运动、静止是相对的，它们与物体相对于选定的参照物有关。同样的道理，如果冰墩墩静止，背景运动了，那么看起来是不是感觉冰墩墩在运动呢？”“那如何将‘事件（按键）—动作（Y坐标变化）这一模型套用在背景上呢？”学生根据教师的不断提问，不断深入学习实践，从而发现如果把背景的Y坐标进行反方向变化，冰墩墩静止，这时即可形成冰墩墩正向移动的视觉体验。这时学生可能又会发现问题：“背景移动，冰墩墩静止，虽然让冰墩墩看上去移动了，但这时静止的障碍物看上去也一起跟着移动了。”这时，教师可以引导学生讨论解决方案，学生通过思考想到“背景移动，冰墩墩静止，障碍物移动，而且背景移动速度要与障碍物移动速度相等”的解决方案，并進行算法的设计。通过探究实践，反复试错、不断反思、批判与修订，从一个个问题的提出到一个个问题的解决，学生在这一过程中提升了解决问题的能力，并能够感受程序设计“反复与递增”“测试与调试”的计算实践过程。

讨论交流，优化算法

“条条道路通罗马”，算法设计更是如此。在项目式编程学习的过程中，教师应该引导学生发散思维，形成多样化的解决方案，并通过讨论交流优化方案。例如，在进行任务3时，学生掌握了“侦测—决策”这一抽象模型，在实际的算法设计时，学生提出了以下几种可能的算法设计方案：冰墩墩侦测障碍物颜色、冰墩墩侦测障碍物这个角色、障碍物克隆体侦测冰墩墩等。然而在讨论交流过程中会发现，第一种方案由于障碍物存在多种颜色，所以以侦测颜色进行算法设计存在偶然性。第二种方案通过尝试，可以很好地侦测冰墩墩与障碍物的碰触，然而变量的计算却出现了一些问题，原因是冰墩墩与障碍物克隆体出现反复碰触导致变量不断增加，所以需要在侦测到克隆体后删除克隆体，然而在冰墩墩角色脚本当中只能删除障碍物本身，无法实现克隆体的删除，因此这一方案也存在漏洞。第三种方案可以实现冰墩墩与障碍物碰触的侦测，同时也能实现在碰触后删除克隆体，变量也能正常变化了。当主要任务完成之后，教师可引导学生通过同伴之间的思维碰撞、交流、互动，激活思维的火花，针对学生提出的多样化优化方案，引导学生对其进行适当的择优与指导。

评价展示，迁移应用

在完成了主要任务之后，教师引导学生梳理总结，迁移应用（如下页表2）。例如，学生学习了“事件（按键）—动作（X/Y坐标变化）”这一模型，可以将其应用在“线上冰壶比赛”中，通过“事件—动作”这一模型控制冰壶石的移动，应用“侦测—决策”判断冰壶石与拱线的碰触情况等。

同时，教师应给予学生足够的时间，根据学生在项目启动阶段所预设的“2022冬奥会宣传的规划框架”，继续完善程序，形成最终的成果。在这一过程中，教师要给予学生脚手架，如知识点微课、学习资料，引导学生通过资料查询、动手实践、同伴互助、教师个别指导等方式完善程序。

成果的完成并不是终点而是补给站，教师可通过呈现辅助描述手册以及评价标准，引导学生描述自己的作品，并结合评价标准对自己以及他人的作品进行评价，如引导学生表达“我的冬奥会宣传作品包括哪几个部分”“我的创意点有……”“我在实践的过程中遇到了什么困难”“我是通过什么方式解决的”“我觉得还有哪些地方可以再进一步完善”等;引导学生评价他人作品，如“我觉得你的作品的优点是……”“但我建议你还可以从这些方面进一步改善作品”“我想请教你这一部分是如何完成的”“我觉得你的作品给了我很大的启发，我可以在……地方改善我自己的作品”等。引导学生在与他人的交流互动中，不断改善作品，再利用再创造、递增与迭代，提升计算观念，获得成长。

总之，从知识点教学转向项目式教学，引导学生在大项目中“提出问题—分析问题—探究实践—讨论交流—评价展示”，并在反复迭代的过程中，引导学生主动与他人分享交流，从而培养学生的计算思维。

参考文献：

[1]Markham，T，Larmer，J.，&Ravitz， J.Project based learning handbook：Aguide to standards-focused project based learning（2nd edition）[M].Novato，CA：Buck Institute for Education，2003.

[2]王春易.從教走向学：在课堂中落实核心素养[M].北京：中国人民大学出版社，2020.

[3]秦琦.面向计算思维培养的可视化程序设计教学实践——以《设计无人驾驶小车》一课为例[J].中国信息技术教育，2021（04）：22-24.

[4]严大虎，苏秀玲，李雨婷.基于问题解决模型的学习者计算思维培养——以编程类课程“数据库技术及应用”的教学为例[J].现代教育技术，2021（02）：109-117.

[5]王卫全，郭苗苗，王晨.通达计算思维的问题驱动教学模式研究[J].中国信息技术教育，2021（05）：34-37.

本文系福建省教育科学“十三五”规划2020年度立项课题“计算思维三维框架在小学编程教学中的应用探究”（立项批准号：FJJKXB20-561）部分研究成果。