基于CEEMD-ARIMA的中美双边贸易额组合预测

朱彦名 张振华

摘要：文章使用互补集合经验模态分解（CEEMD）和自回归移动平均（ARIMA）组合预测模型对中美双边贸易进出口总额进行建模预测。传统ARIMA模型的拟合精度较低，CEEMD-ARMA组合相比传统时间序列模型预测精度更高，有效解决了原始数据的非平稳性。仿真结果表明，该模型优于其他模型，能够以一定的精度预测中美双边贸易额走势。

关键词：CEEMD;ARIMA;组合预测;中美双边贸易额

一、引言

改革开放以来，我国的经济迅速发展，进出口贸易的快速增长功不可没。对外贸易作为拉动经济发展的三辆马车之一，合理的预测其发展走势是必不可少的，这对制定未来贸易战略方针具有重大的指导性作用，对外贸易市场的进一步擴大，参与全球化经济竞争，保证我国经济平稳快速增长，保证国民经济平稳增长具有积极的意义。

进出口贸易是拉动经济增长和实现对外交流的重要工具，近年来我国对外贸易发展迅速，尤其是出口经济。但随着国际形势的日益复杂化和我国高新技术产业核心竞争力升级，近年来中美贸易摩擦日益严重。美国以“贸易逆差”为由对中国发动贸易战，实则是为了遏制中国的崛起。自2018年3月以来，美国针对中国推出三轮提高关税政策。另一方面，美国指责中国“窃取知识产权”和“强迫技术转让”，体现出美国试图妨碍中国发展高新技术。中美关税增加，贸易摩擦的产生必然对中美双边贸易产生影响。科学预测中美贸易的发展趋势，对我国制定中美贸易战略方针有着一定指导性作用。

目前针对进出口贸易额的预测应用分析，我国学者所选择的预测方法各有不同，但预测方法多为单一模型。吴昕（2016）基于向量自回归模型，采取定量与定性分析相结合的方式对我国进出口贸易趋势进行了预测研究;陈锐（2015）基于“监督分组”主成分回归对进出口贸易值与增速进行了预测。回归预测的缺陷在于只提取了线性规律而对非线性规律则无法进一步进行挖掘。杜江（2010）基于模糊时间序列模型，针对我国对外贸易的进口水平进行了预测;陈蔚（2015）使用人工BP神经网络方法和ARIMA模型，对我国对外贸易的进口与出口贸易额进行了预测;王雅琴（2018）采用时间序列分析和弹性分析法就中美贸易战局势下对我国煤炭进出口贸易额进行了预测。目前传统单一模型预测结果的平均绝对百分误差多在10%～40%间，为了提高预测的精度，近年来更多的学者将神经网络、时间序列、支持向量机（SMV）、灰色预测、模糊算法等相结合，形成多方法并用的组合预测算法模型。舒服华（2018）运用小波变换和灰色DGM（2，1）模型相结合的方法预测我国进出口贸易总额。本文选用时间序列预测模型，结合适用于非平稳时间序列的CEEMD分解法构建组合预测模型，该模型相比其他模型能够有效地解决时间序列数据的非平稳性问题，且预测精度更高。

二、相关模型理论

（一）时间序列模型

根据时间序列模型的建模步骤，首先对原时间序列需进行平稳性检验和白噪声检验。

1. 时间序列预处理

（1）平稳性检验。图检验法和单位根检验法是常见的平稳性检验方法。图检验法利用了平稳序列具有短期相关的特性，对序列自相关系数进行观察，若其较快衰减到零而后在零附近波动，则原序列为平稳的。而常见单位根检验法有DF检验、ADF检验和PP检验，若检验出原序列存在单位根，则序列为非平稳时间序列，反之则为平稳序列。在实际分析过程中，由于经济发展趋势，大多数的经济时间序列都是非平稳的。因此要对原序列进行平稳化，若原序列为非平稳时间序列，可通过对数处理和差分处理等方式将非平稳时间序列平稳化。

（2）白噪声检验。白噪声检验也称作纯随机性检验，其目的是检验原时间序列是否为白噪声序列。白噪声序列的特点是任意两个时点的随机变量都无关系，即原序列中没有任何动态规律可以为人所用。因此白噪声序列是无法进行预测分析的。只有通过白噪声检验，也就是说原序列为非白噪声序列，预测建模才有意义。

2. 平稳时间序列建模

（1）自回归模型。p阶自回归过程AR（p）的表达式为：

Yt=c+■？覬iYt-i+εt（1）

自回归模型讨论的是t时刻的序列值Yt与过去时序值Yt-i和常数项c的相关关系，φi（i=1，2，…，p）表示自回归系数，且φp≠0，εt表示残差，残差应符合白噪声序列。

（2）移动平均模型。q阶移动平均模型MA（q）的表达式为：

Yt=c+■θiεt-i+εt（2）

移动平均模型讨论的是t时刻的序列值Yt与现在干扰值εt以及过去随机干扰值εt-i的相关关系。εt为t时刻的干扰值，c表示常数，θi（i=1，2，…，q）表示移动平均系数，且θq≠0。

（3）自回归移动平均模型。自回归移动平均模型讨论的是t时刻的序列值Yt与现在干扰值εt、过去随机干扰值εt-i，以及过去时序值Yt-i和常数项c的相关关系，即ARMA（p，q）模型、表达式为：

Yt=c+■？覬iYt-i+εt-■θiεt-i（3）

3.非平稳时间序列建模

单整自回归移动平均模型，即ARIMA（p，d，q）模型，表达式为：

（1-■？覬iBi）（1-B）dYt=（1+■θiBi）εi（4）

ARIMA模型可用于非平稳时间序列，其中p为自回归系数，q为移动平均系数，d表示差分阶数。实际上ARIMA（p，d，q）模型可从ARMA（p，q）模型通过d阶差分得到，即将非平稳时序通过差分的方式使原序列平稳化，再采用ARMA模型进行建模的过程。

（二）CEEMD分解

1. EMD分解思想

经验模态分解法，也可称为EMD分解法是一种自适应信号时频处理方法。EMD方法由N. E. Huang（1998，2009）提出，该分解方法适合处理非线性、非平稳信号序列。相比较于传统的小波分解，EMD分解更能保持原有序列的信息，信号损失更小，且局部表现能力更优，更适合对高频、非线性的经济宏观数据进行处理。通过EMD方法分解得出来的分量被称作本征模函数（Intrinsic Mode Function，简称IMF）。分解步骤如下：

（1）找出原始信号s（t）所有的极大值点，并将其用三次样条函数拟合出原始信号的上包络线;同理，找出信号所有极小值点，拟合出下包络线。

（2）计算上下包络线的均值，记为m1（t），那么原信号的第一個IMF分量为：

h1（t）=s（t）-m1（t）（5）

经验模态分解法将信号分解为一系列表征时间尺度的IMF分量，使得各IMF分量是窄带信号，即IMF分量必须满足下面两个条件：在整个信号程度上，极值点和过零点的数目必须相等或者至多只相差一个;在任意时刻，由极大值点定义的上包络线和由极小值点定义的下包络线的平均值为零，即信号的上下包络线关于时间轴对称。具体步骤如下：

找出原始信号x（t）所有的极值点，使用三次样条函数拟合出原始信号的上包络线emax（t）和下包络线emin（t）;

计算上下包络线均值，记为m1（t），用原始信号x（t）减去m1（t）：

m1（t）=（emintm1（t）+emaxm1（t））/2（6）

h1（t）=x（t）-m1（t）（7）

（3）对残余的h1（t）作为原始信号重复上述步骤，直到得出的余量满足以下两个条件为止：函数在整个时间范围内，局部极值点和过零点的数目必须相等，或最多相差一个;在任意时刻点，局部最大值的包络（上包络线）和局部最小值的包络（下包络线） 均值为零。此时得到第一个IMF分量，用IMF1（t）表示，此分量为原序列x（t）中最高频分量。

h1k（t）=h1（k-1）（t）-m1k（t）（8）

c1（t）=h1k（t）（9）

（4）将分量IMF1（t）从原序列x（t）中剔除，得到残余序列r1（t）：

r1（t）=x（t）-IMF1（t）（10）

将残余序列r1（t）作为原始信号，重复上述步骤，则可以得到第二个分量IMF2（t），如此循环：

r2（t）=r1（t）-IMF2（t）（11）

rn（t）=rn-1（t）-IMFn（t）（12）

到此原始序列x（t）则被分解成n个IMF分量，其频率由高频逐渐到低频，以及残余函数rn（t），残余函数rn（t）代表了序列的平均趋势，

2. CEEMD基本思想

互补集合模态分解（complementary ensemble empirical mode decomposition，简称CEEMD）是由Yeh（2010）等人从EMD方法和EEMD方法不断优化而来。相比EMD方法，他解决了EMD方法所存在的模态混叠效应与频谱泄露问题，相比EEMD方法，他能更高效地抹去重组信号中的残余辅助噪声，在一定程度上提高了效率。其主要步骤为：

第一步：向原始序列x（t）中添加n组正、负成对的辅助白噪声序列，得到

M■M■=1 11 -1x（t）N（13）

其中，N表示辅助白噪声，加入白噪声后重组数据为M1、M2。

第二步：对第一步处理后的数据进行EMD处理。可以得到IMFij，即第i个分量的第j个IMF。

第三步：计算均值得到

IMFj=■■IMFij（14）

其中，IMFj表示CEEMD分解后最终得到的第j个IMF分量，n为白噪声组数。

三、实验研究

（一）数据获取

考虑数据的连续性及有效性，本文选取了2008年5月至2019年12月共140个数据作为本文核心数据，下文皆以此月度数据为核心，数据来源于中国商务部国别报告（https：//countryreport.mofcom.gov.cn/）。此外，为了提高预测结果的稳健性，本文选取了1985年第一季度至2020年第二季度共142个季度数据，数据来源于Wind数据库。月度与季度数据原始数据时序图（见图1、图2）。

（二）时间序列预测模型

1. 时间序列预处理

经济学上的时间序列通常呈现非平稳性，通过观察中美双边贸易进出口总额的时间序列图，可以发现其整体存在着上升趋势。本文采用ADF检验法对序列平稳性进行检验，ADF检验结果表明，t值为-2.401，均大于1%、5%、10%显著水平下的临界值，进一步表明中美双边贸易进出口总额时间序列为非平稳序列。

中美双边贸易的非平稳性通常是宏观经济波动和季节波动所造成的，欲将原始序列平稳化，本文先对原序列进行季节差分，再进行一阶差分。差分处理后的数据如图3所示，可见处理后的序列基本在零值附近波动，无明显的上升趋势。将处理后的序列再进行ADF检验，结果显示，t值为-4.375，此时1%水平的临界值为-3.493、5%水平的临界值为-2.889、10%水平的临界值为-2.581，t值小于各个显著水平下的临界值，同时p值小于0.01，表明处理后的序列不存在单位根。将处理后的时间进行Ljung-Box检验，发现其p值小于0.01，表明差分后的序列不是白噪声序列。由此可见，经过预处理后的序列符合平稳非白噪声序列，可以进行下一步建模。

2. 模型定阶

中美双边贸易进出口总额时间序列进行差分后为平稳序列，建立ARIMA（p，d，q）模型，数据预处理中进行了季节差分和一阶差分，因此可以将季节差分后的数据作为原始数据，再取差分阶数d=1。由自相关函数图和偏自相关系数图（见图4），可以确定模型中p与q的阶数，本文的预选模型为ARIMA（2，1，2）和ARIMA（2，1，3）。

3. 建模

利用R.Studio软件，本文分别对预处理后的数据进行ARIMA（2，1，2）和ARIMA（2，1，3）建模，参数估计的结果如表1所示。

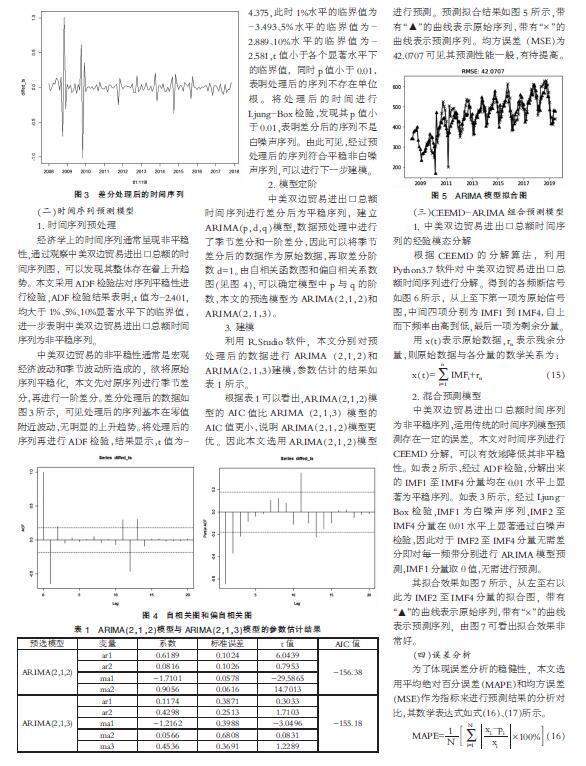
根据表1可以看出，ARIMA（2，1，2）模型的AIC值比ARIMA（2，1，3）模型的AIC值更小，说明ARIMA（2，1，2）模型更优。因此本文选用ARIMA（2，1，2）模型进行预测。预测拟合结果如图5所示，带有“▲”的曲线表示原始序列，带有“×”的曲线表示预测序列。均方误差（MSE）为42.0707可见其预测性能一般，有待提高。

（三）CEEMD-ARIMA组合预测模型

1. 中美双边贸易进出口总额时间序列的经验模态分解

根据CEEMD的分解算法，利用Python3.7软件对中美双边贸易进出口总额时间序列进行分解。得到的各频断信号如图6所示，从上至下第一项为原始信号图，中间四项分别为IMF1到IMF4，自上而下频率由高到低，最后一项为剩余分量。

用x（t）表示原始数据，rn表示残余分量，则原始数据与各分量的数学关系为：

x（t）=■IMFi+rn（15）

2. 混合预测模型

中美双边贸易进出口总额时间序列为非平稳序列，运用传统的时间序列模型预测存在一定的误差。本文对时间序列进行CEEMD分解，可以有效地降低其非平稳性。如表2所示，经过ADF检验，分解出来的IMF1至IMF4分量均在0.01水平上显著为平稳序列。如表3所示，经过Ljung-Box检验，IMF1为白噪声序列，IMF2至IMF4分量在0.01水平上显著通过白噪声检验，因此对于IMF2至IMF4分量无需差分即对每一频带分别进行ARIMA模型预测，IMF1分量取0值，无需进行预测。

其拟合效果如图7所示，从左至右以此为IMF2至IMF4分量的拟合图，带有“▲”的曲线表示原始序列，带有“×”的曲线表示预测序列，由图7可看出拟合效果非常好。

（四）误差分析

为了体现误差分析的稳健性，本文选用平均绝对百分误差（MAPE）和均方误差（MSE）作为指标来进行预测结果的分析对比，其数学表达式如式（16）、（17）所示。

MAPE=■■■×100%（16）

MSE=■■（xi-pi）2（17）

其中，xi表示原始序列的真实数据，pi表示预测结果，N为样本数。

本文采用CEEMD分解法，从月度数据和季度数据两个层面与传统时间序列模型进行对比验证，另外在模型定阶上对比了ACF/PACF图形定阶法与自动定阶法。得出的平均绝对百分误差（MAPE）以及均方误差（MSE）如表4所示。

从表4中可以看出，无论是季度数据还是月度数据，CEEMD-ARIMA组合预测模型的表现都明显优于传统时间序列模型，平均绝对百分误差（MAPE）和均方误差（MSE）也更小，因此采用CEEMD-ARIMA组合预测模型的精度更高，预测效果更佳。此外，对比月度数据和季度数据可以看出，在近乎相同数据量的情况下，时间跨度小的月度数据比跨度大的季度数据预测结果更加精确，因此用月度数据进行预测更加具有可靠性。

四、结语

本文采用了互补集合经验模态分解与ARIMA的组合预测方法建模，较之于传统的单一时间序列模型使用差分等方法处理序列的非平稳，采用分解的方式对原始序列的信息损失更小，且计算精度更高。通过对非平稳的中美双边贸易额的实际数据实验对比，可以看出互补集合经验模态分解与ARIMA的组合模型在非平稳时间序列预测中比传统模型预测效果更加良好。

本文给予了中美两国进出口贸易的预测，一方面发现月度数据比季度数据预测效果更好，另一方面验证了CEEMD-ARIMA预测模型的实用性。能否就此将此方法应用在两国出口贸易、进口贸易，乃至某行业某领域进出口贸易，还有待探究。

参考文献：

[1]吴欣，王雯婧.我国进出口贸易潜力预测研究——基于VAR分析方法[J].经济研究参考，2016（33）：34-39.

[2]陈锐.基于“监督分组—残差”主成分回归的进出口贸易预测[J].统计与决策，2015（13）：112-114.

[3]杜江，李玉蓉，钟菲菲.基于模糊时间序列对我国对外贸易中的进口水平的预测[J].统计与决策，2010（23）：112-114.

[4]陈蔚.基于线性ARIMA与非线性BP神经网络组合模型的进出口贸易预测[J].统计与决策，2015（22）：47-49.

[5]王雅琴.中美贸易战下我国煤炭进出口预测[J].中国煤炭，2018，44（10）：9-13.

[6]舒服华.基于小波DGM（2，1）模型的我國进出口贸易额预测[J].保定学院学报，2018，31（03）：17-23.

[7]Norden E.Huang，Zheng Shen，Steven R.Long， et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J].1998，454（1971）：903-995.

[8]Wu Z， Huang N E. Ensemble Empirical Mode Decomposition：A Noise-Assisted Data Analysis Method[J].Advances in Adaptive Data Analysis，2009，1（01）：1-41.

[9]Yeh J R，Shieh J S，Huang N E. Complementary Ensemble Empirical Mode Decomposition：a Novel Noise Enhanced Data Analysis Method[J].Advances in Adaptive Data Analysis，2010，2（02）：135-156.

*本文受全国统计科学研究重点项目资助（项目号2016LZ18）。

（作者单位：广东外语外贸大学。张振华为通讯作者）