面向异构物理机的云任务调度策略及性能优化①
2021-11-14范宝芝王开宇白小军金顺福
范宝芝 王开宇 白小军 金顺福
(燕山大学信息科学与工程学院 秦皇岛066004)
0 引言
随着无线通讯技术的发展,网络应用程序的使用越来越多。移动设备负载能力不足的问题日趋明显,云计算为移动设备的任务卸载提供支持[1]。值得注意的是,不断增长的云应用导致云数据中心消耗着巨大的能源,对环境也产生了恶劣的影响。研究发现,按照每年40%~60%的增长率估算,到2030 年云数据中心的能源消耗将达到8000 TWh[2]。绿色云计算是社会进步的必然趋势,也是实现可持续发展的前提。缓解云数据中心的高耗能问题是云计算研究的重点内容之一。
文献[3]提出了一种动态迁移虚拟机的调度方法,通过建立一个虚拟机放置/迁移的平台,使用两个调度程序分别调度预期的负载和未预期的负载,有效降低了云数据中心的功耗。文献[4]提出了一种动态的空闲间隔预测方案,该方案可以估计未来中央处理器(central processing unit,CPU)空闲间隔长度,选择考虑成本效益的休眠状态以最小化运行功耗,并提高CPU 的利用率。以上文献专注于降低云系统的能源消耗,却忽略了云用户对响应性能的需求。
考虑到云用户对响应性能的需求,文献[5]提出了一种基于(N,T) 休眠机制的云计算中心节能策略。结合唤醒阈值N及长度为T的休眠计时器,建立多重同步休假随机模型。利用改进飞蛾扑火优化算法,给出了节能策略的联合优化方案,实验证实所提策略在保证用户响应性能的基础上,有效降低了系统能耗。文献[6]提出了一种基于动态阈值的服务器唤醒策略。该策略综合考虑用户端的任务情况和服务器的能耗成本,动态调整任务请求数的阈值,并根据时间优先级唤醒服务器。与静态阈值的服务器唤醒策略相比,该策略有效降低了云计算系统的能耗开销。以上研究专注于云系统本身,未考虑产生任务的移动设备及移动设备自身的处理能力。
本文综合考虑云用户响应性能及云系统的能源消耗,基于部分用户任务在移动设备本地处理器执行的实际情况,提出一种移动设备本地处理器持续工作和云端物理机内虚拟机同步休眠的任务调度策略。针对云端异构物理机的不同服务速率,在远程云端建立多个带有同步多重休假的M/M/ck排队模型。利用拟生灭过程和矩阵几何解给出系统模型的稳态分布,通过系统实验揭示任务平均响应时间与系统平均运行功率的变化趋势。构造系统成本函数,引入Logistic 映射混沌机制改进传统鲸鱼优化算法,给出最优任务分配策略,实现系统成本的最小化。
1 任务调度策略及系统模型
1.1 任务调度策略
针对移动设备存储空间不足且处理能力有限等问题,借助于远程云端的帮助,移动设备任务负载能够有效地得到均衡。在任务调度器的协调下,将移动设备产生的任务分为两部分,一部分任务分配到本地处理器接受服务,另一部分任务则卸载到远程云端的虚拟机上接受服务。
远程云端部署多个异构物理机,物理机的集合表示为S={S1,S2,…,Sn},| S|=n。通过虚拟化技术在物理机Sk(k=1,2,…,n) 上部署ck(ck≥1)个云虚拟机。假设部署在同一台物理机上的虚拟机同构,不同物理机上的虚拟机异构[7]。给出由本地移动设备和远程云端组成的体系结构,如图1 所示。

图1 移动设备与远程云端构成的体系结构
传统云服务中,云服务器一直处在活跃状态,增加了远程云端的能源消耗。休眠机制是一种有效减少能源消耗的人为手段。借助于虚拟化技术,在同一台物理机上的虚拟机中引入周期性同步休眠机制,不同物理机上的虚拟机引入周期性异步休眠机制。在每个物理机上设置一个休眠定时器。当物理机上的全部任务结束服务时,该定时器触发,部署在该物理机上的全部虚拟机同时进入休眠状态。不同物理机上的定时器的触发相互独立,也就是说,一个物理机上的虚拟机的休眠或唤醒,与另一个物理机上虚拟机无关。
基于所提出的体系结构,远程云端上的虚拟机具有3 种状态:活跃状态、空闲状态和休眠状态。虚拟机的状态转换过程如图2 所示。
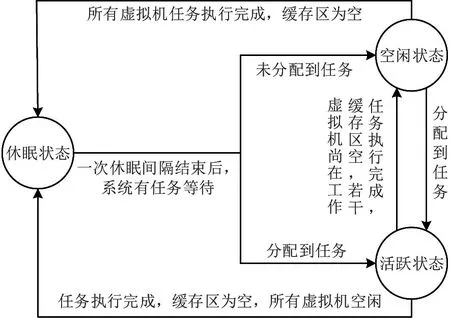
图2 虚拟机的状态转移过程
(1) 活跃状态。处于活跃状态的虚拟机为某一个任务提供服务。虚拟机服务完成当前任务后,按先来先服务规则为缓存区中等待的任务提供服务。若缓存区空,但其他虚拟机未全部空闲,则该虚拟机由活跃状态切换到空闲状态。若缓存区空且所有虚拟机空闲,则该虚拟机与其他虚拟机同步切换到休眠状态。
(2) 空闲状态。处于空闲状态的虚拟机,可以随时为分配到的任务提供服务,也可以与其他虚拟机同步进入休眠状态。若分配到任务,空闲虚拟机可以立即切换到活跃状态。若所有虚拟机全部执行完成所分配的任务且缓存区空,该虚拟机与其他虚拟机同步切换到休眠状态。
(3) 休眠状态。处于休眠状态的虚拟机暂时不再为任务提供服务。当虚拟机处于休眠状态时,新到达任务在系统缓存区中排队等待。当一个物理机的休眠定时器到期时,若系统缓存区空,重新启动休眠定时器,其上的虚拟机同时开始下一个休眠间隔,多个休眠间隔构成一个休眠期;若系统缓存区不空,全部虚拟机则同时结束休眠,依次处理系统缓存区滞留的任务。分配到任务的虚拟机由休眠状态切换到活跃状态,未被分配到任务的虚拟机由休眠状态切换到空闲状态。
1.2 系统模型
将移动设备视为连续工作的M/M/1 排队,远程云端的每一个物理机视为虚拟机同步多重休假的M/M/ck排队,建立系统模型。
令任务的产生服从参数为λ(0<λ <+∞) 的指数分布。假设一个物理机上的虚拟机服务能力相同,令物理机Sk(k=1,2,…,n) 上的虚拟机服务一个任务的时间服从参数为μk(0<μk <+∞) 的指数分布,令物理机休眠定时器长度服从参数为θk(0<θk <+∞) 的指数分布。
假设任务在本地执行的概率为q(0 ≤q≤1),任务卸载到远程云端的概率为1-q。卸载到远程云端的任务将分配到某一个物理机上。假设某个任务分配到物理机Sk的概率为ξk,则ξ1+ξ2+…+ξn=1。基于以上假设,本地任务的到达服从参数为λ0=λq的指数分布,物理机Sk上的任务到达服从参数λk=λ(1-q)ξk的指数分布。假设物理机具有无限容量的缓存。
本地移动设备的系统服务强度ρ0定义为一个本地任务的服务时间内分配到本地移动设备的平均任务数。ρ0表示为

其中,μ0为本地移动设备的服务率。
云端物理机Sk的系统服务强度ρk定义为一个云端任务的服务时间内卸载到云端的平均任务数。ρk表示为
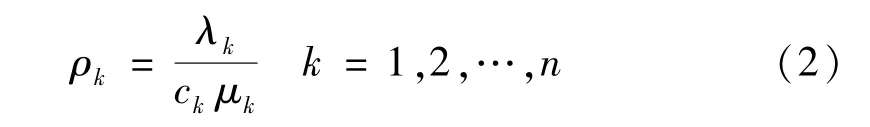
为了使系统稳定,令本地移动设备的系统服务强度ρ0和云端物理机Sk的系统服务强度ρk均小于1。
令随机变量Xk(t)=i(i=0,1,…) 表示时刻t物理机Sk内的任务数。令随机变量Yk(t)=j(j=0,1) 表示时刻t物理机Sk上虚拟机所处的状态。当j=0 时,表示虚拟机处在休眠状态;当j=1 时,表示虚拟机处在活跃状态。{(Xk(t),Yk(t)),t≥0} 构成一个二维时间连续马尔科夫链,其状态空间表示为
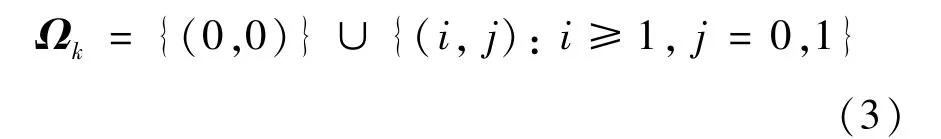
令πk(i,j) 表示稳态下物理机Sk的系统水平为i、系统阶段为j的概率分布。πk(i,j) 表示为
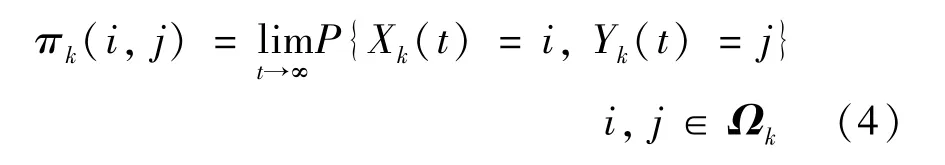
令πk(0)=πk(0,0) 表示为稳态下系统水平为0 的概率向量,令πk(i)=(πk(i,0),πk(i,1))表示为稳态下系统水平为i的概率向量。二维连续时间马尔可夫链{(Xk(t),Yk(t)),t≥0} 的稳态概率分布Πk表示为
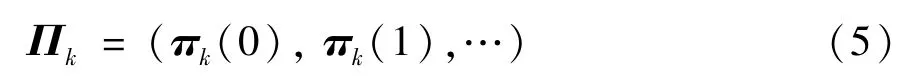
2 系统模型的稳态分析
假设远程云端部署了n个异构物理机,物理机Sk上部署了ck个虚拟机。物理机Sk可看作一个独立的同步多重休假M/M/ck排队[8]。物理机Sk上虚拟机的状态转移机制如图3 所示。

图3 物理机Sk 上虚拟机的状态转移
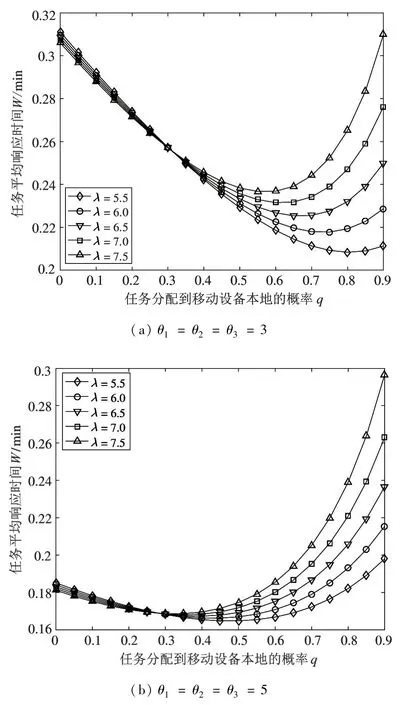
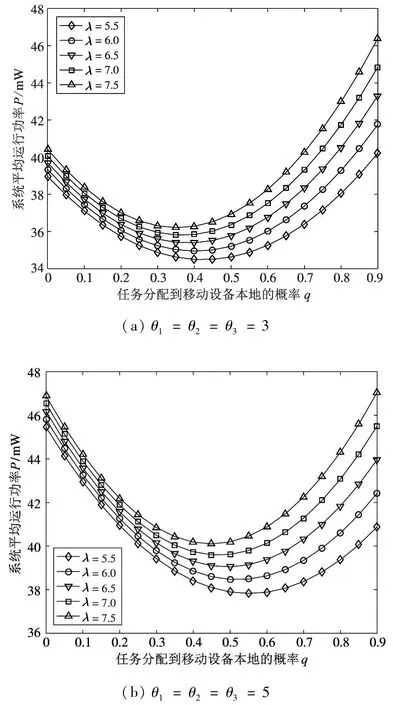
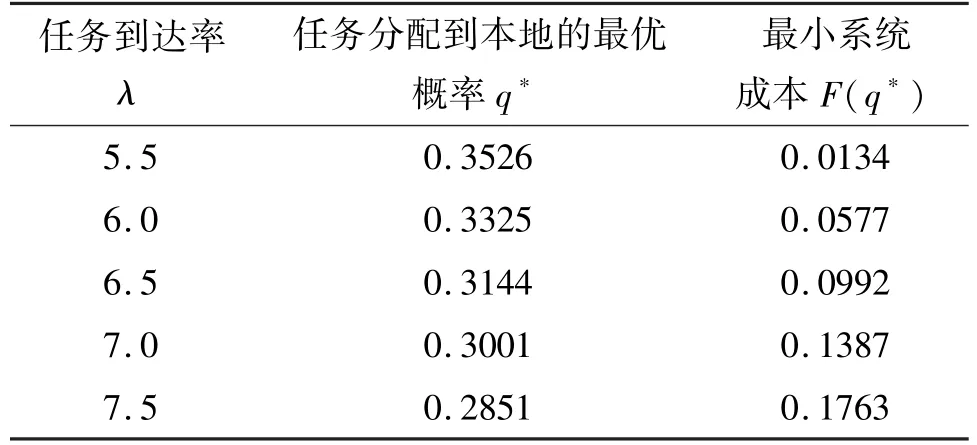
由图3 可以分析出一个物理机中多个虚拟机的状态转移过程。当j=0 时,物理机Sk上ck个虚拟机全部处于休眠状态。当j=1 时,若系统内有i 令Qk表示二维连续时间马尔可夫链{(Xk(t),Yk(t)),t≥0} 的一步转移率矩阵,Qk(x,y) 表示经过一步转移后,系统水平从x(x=0,1,…) 到y(y=0,1,…) 的转移率子阵。为了表述方便,将Qk(x,x -1)、Qk(x,x) 与Qk(x,x +1) 分别记为Bk(x)、Ak(x) 与Ck(x)。 (1) 当x=0 时,虚拟机一定处于休眠状态,且缓存区为空。当无任务到达时,系统水平和系统阶段均保持不变,Ak(0) 退化为一个数值,Ak(0)=-λk。若有一个任务到达,系统水平由x=0 变为x=1,系统阶段不变,转移率为λk,Ck(0) 为1 ×2 维矩阵,表示为 (2) 当x=1 时,虚拟机既可能处于休眠状态,也可能处于活跃状态。 首先,讨论系统水平下降的情形。当虚拟机处于休眠状态时,任务不可能产生离去。当虚拟机处于活跃状态时,若处理完成一个任务,系统水平由x=1 变为x=0,虚拟机由活跃状态切换到休眠状态,系统阶段由j=1 变为j=0,转移率为μk。Bk(1) 为2 ×1 维矩阵,表示为 其次,讨论系统水平不变的情形。当虚拟机处于休眠状态时,若无任务到达且休眠定时器未到期,转移率为-(λk+θk);若休眠定时器到期,虚拟机由休眠状态切换到活跃状态,系统阶段由j=0 变为j=1,转移率为θk。当虚拟机处于活跃状态时,若无任务到达且虚拟机未处理完成当前任务,转移率为-(λk+μk),此时,虚拟机无法进入休眠状态。Ak(1) 为2 ×2 维矩阵,表示为 最后,讨论系统水平增加的情形。无论虚拟机处于休眠状态还是活跃状态,若有一个任务到达,系统水平由x=1 变为x=2,系统阶段不变,转移率为λk。Ck(1) 为2 ×2 维矩阵,表示为 (3) 当1 首先,讨论系统水平下降的情形。当虚拟机处于休眠状态时,任务不可能产生离去。当虚拟机处于活跃状态时,若处理完成一个任务,系统水平由x变为x -1,转移率为xμk,此时,物理机Sk还存在未处理完成的任务,虚拟机无法进入休眠状态。Bk(x)为2 ×2 维矩阵,表示为 其次,讨论系统水平不变的情形。当虚拟机处于休眠状态时,若无任务到达且休眠定时器未到期,转移率为-(λk+θk);若休眠定时器到期,虚拟机由休眠状态切换到活跃状态,系统阶段由j=0 变为j=1,转移率为θk。当虚拟机处于活跃状态时,若无任务到达且虚拟机未处理完成当前任务,转移率为-(λk+xμk),此时,虚拟机无法进入休眠状态。Ak(x) 为2 ×2 维矩阵,表示为 最后,讨论系统水平增加的情形。无论虚拟机处于休眠状态还是活跃状态,若有一个任务到达,系统水平由x变为x +1,系统阶段不变,转移率为λk。Ck(x) 为2 ×2 维矩阵,表示为 (4) 当x >ck时,虚拟机仍然可能处于休眠状态或者活跃状态。 首先,讨论系统水平下降的情形。当虚拟机处于休眠状态时,任务不可能产生离去。当虚拟机处于活跃状态时,有ck个任务同时接受服务,若处理完成一个任务,系统水平由x变为x -1,转移率为ckμk,此时,虚拟机同样无法进入休眠状态。Bk(x)为2 ×2 维矩阵,表示为 其次,讨论系统水平不变的情形。当虚拟机处于休眠状态时,若无任务到达且休眠定时器未到期,转移率为-(λk+θk);若休眠定时器到期,虚拟机由休眠状态切换到活跃状态,系统阶段由j=0 变为j=1,转移率为θk。当虚拟机处于活跃状态时,若无任务到达且虚拟机未处理完成当前任务,转移率为-(λk+ckμk),此时,虚拟机无法进入休眠状态。Ak(x) 为2 ×2 维矩阵,表示为 最后,讨论系统水平增加的情形。无论虚拟机处于休眠状态还是活跃状态,若有一个任务到达,系统水平由x变为x +1,系统阶段不变,转移率为λk。Ck(x) 为2 ×2 维矩阵,表示为 由上述分析可得,转移率子阵Ak(x) 与Bk(x)均从系统水平ck开始重复,Ck(x) 从1 开始重复。将重复的Ak(x) 与Bk(x) 分别用Ak与Bk来表示,将重复的Ck(x) 用Ck来表示,则马尔可夫链{(Xk(t),Yk(t)),t≥0} 的一步转移率矩阵Qk可以表示为如下分块形式。 从一步转移率矩阵Qk的结构可知,状态的转移只发生在相邻的系统水平之间。因此,二维连续时间马尔可夫链{(Xk(t),Yk(t)),t≥0} 可以看成一种拟生灭过程。该过程正常返的充分必要条件是矩阵方程 的最小非负解Rk(也称为率阵)的谱半径Sp(Rk)<1。 由Qk子阵结构,可设率阵,将Ak、Bk、Ck与Rk代入式(17),可得率阵Rk如下。 根据率阵Rk的解析结果,可以看出率阵Rk的谱半径,所以二维马尔可夫链{(Xk(t),Yk(t)),t≥0} 正常返。利用所求得的率阵Rk,构造方阵B[Rk]如下。 由平衡方程及归一化条件可得如下方程组: 其中,Ι为单位矩阵,e为全1 列向量。 系统的稳态分布表示为 其中,πk(0,0) 由归一化条件给出如下。 任务响应时间定义为从任务的产生时刻开始,到任务结束服务离开系统为止所经历的时间段。 分配到本地执行的任务平均响应时间W0包括任务在本地缓存区的平均等待时间与在本地处理器的平均服务时间。根据排队模型M/M/1 的解析结果,给出本地任务平均响应时间W0的表达式为 卸载到远程云端的任务平均响应时间包括任务在缓存区的平均等待时间与在虚拟机上的平均服务时间。由第2 节给出的系统模型的稳态分析结果计算出平均等待队长的表达式,进一步利用Little 公式[9]得出物理机Sk上任务平均响应时间Wk的表达式为 任务在本地执行的概率为q(0 ≤q≤1),卸载到远程云端的概率为1-q,卸载到远程云端的任务分配给物理机Sk的概率为ξk。综合式(24)给出的本地任务平均响应时间W0和式(25)给出的物理机Sk任务平均响应时间Wk,得出任务平均响应时间W为 移动设备处于活跃状态时,其处理器高速运转,令其运行功率表示为。移动设备处于空闲状态时,其处理器低速运转,令其运行功率表示为。显然,。移动设备平均运行功率P0为 其中,ρ0表示为移动设备处于活跃状态的概率。 综合式(27)给出的移动设备平均运行功率P0和式(28)给出的物理机Sk平均运行功率Pk,得出系统平均运行功率P的表达式为 为量化任务到达率λ、休眠参数θk、任务分配到移动设备本地的概率q及任务卸载到远程云端物理机Sk上的概率ξk对云系统任务调度策略的影响,进行系统实验,刻画以分钟(min)为单位的任务平均响应时间与以毫瓦(mW)为单位的系统平均运行功率的变化趋势。系统实验所用计算机的处理器为Intel(R) Core(TM) i7-4790,运行频率为3.60 GHz,内存为8 GB。系统实验与系统优化在Matlab R2016a的环境下实现。 在保证系统稳定,即本地服务强度ρ0<1 与远程云端物理机的服务强度Max(ρ1,ρ2,…,ρn)<1的约束下,设置如表1 所示的系统实验参数。 表1 系统实验参数设置 使用表1 设定的参数,固定卸载到远程云端物理机S1、S2、S3的概率(ξ1=0.2225、ξ2=0.3432、ξ3=0.4343),考虑不同的休眠参数θk(k=1,2,3)进行系统实验,图4 刻画了任务到达率λ与任务分配到移动设备本地的概率q对任务平均响应时间W的影响。 横向观察图4,随着任务分配到移动设备本地的概率q的增大,任务平均响应时间W先呈现下降趋势,在到达最低点之后开始上升。当任务分配到移动设备本地的概率较小时,任务在远程云端物理机的响应时间占平均响应时间的主导地位。随着任务分配到移动设备本地的概率的增大,任务在远程云端物理机缓存区的平均等待时间随之减少,任务平均响应时间降低。当任务分配到移动设备本地的概率较大时,任务在移动设备的响应时间占平均响应时间的主导地位。随着任务分配到移动设备本地的概率的增大,任务在移动设备本地的平均等待时间随之增大,任务平均响应时间上升。 图4 任务平均响应时间的变化趋势 纵向观察图4,随着任务到达率λ的增大,任务平均响应时间W的变化趋势与任务分配到移动设备本地的概率q有关。当任务分配到移动设备本地的概率较小时,更多的任务卸载到远程云端物理机接受服务。任务到达率越大,虚拟机进入休眠状态的概率越小,任务平均响应时间随之减少。当任务分配到移动设备本地的概率较大时,分配到移动设备本地的任务越多,任务在移动设备本地的等待时间变长,任务平均响应时间随之增大。 对比观察图4(a)和图4(b),随着休眠参数θk(k=1,2,3) 的增大,任务平均响应时间W呈现下降趋势。任务分配到本地设备的概率较小时,更多的任务卸载到远程云端物理机。当休眠参数较小时,任务在缓存区中等待虚拟机结束休眠的时间较长,导致任务平均响应时间加大。这种情况下,本文所提策略中的休眠机制对任务平均响应时间的影响较大。而当休眠参数较大时,任务在缓存区中等待虚拟机结束休眠的时间相对缩短,任务平均响应时间随之减少。这种情况下,本文所提策略中的休眠机制对任务平均响应时间的影响较小。 图5 刻画了任务到达率λ与任务分配到移动设备本地的概率q对系统平均运行功率P的影响。 横向观察图5,随着任务分配到移动设备本地的概率q的增大,系统平均运行功率P先呈现下降趋势,在到达最低点之后开始逐渐上升。当任务分配到移动设备本地的概率较小时,更多的任务卸载到远程云端物理机接受服务,远程云端物理机的运行功率占系统平均运行功率P的主导地位。随着任务分配到移动设备本地的概率增大,卸载到远程云端物理机的任务量减少,物理机上的虚拟机处于活跃状态的可能性减小,物理机的运行功率下降,系统平均运行功率下降。当任务分配到移动设备本地的概率较大时,更多的任务分配到移动设备本地接受服务,移动设备本地的运行功率占系统平均运行功率P的主导地位。随着任务分配到移动设备本地的概率增大,分配到移动设备本地的任务增多,移动设备功耗增大,系统平均运行功率上升。 纵向观察图5,随着任务到达率λ的增大,系统平均运行功率P随之增大。任务到达率越大,意味着任务量越多,移动设备与物理机的功耗增大,系统平均运行功率上升。 对比观察图5(a)和图5(b),随着休眠参数θk(k=1,2,3) 的增大,系统平均运行功率P呈现上升趋势。随着休眠参数的增大,虚拟机进入休眠状态的可能性降低,而虚拟机处于活跃状态或空闲状态的可能性增大,系统平均运行功率上升。 图5 系统平均运行功率的变化趋势 比较图4 与图5 可以看出,最低的平均响应时间所对应的任务分配到移动设备本地的概率无法实现最低的能耗水平。实际应用中,需根据实际应用的业务特点设置任务分配到移动设备本地的概率。 系统实验所揭示的任务平均响应时间和系统平均运行功率的变化规律表明,任务到达率、休眠参数与任务分配到移动设备本地的概率是影响系统性能的重要因素。在不同的任务到达率下,合理设置任务分配到移动设备本地的概率能够实现响应性能与能耗水平的合理均衡。 对任务平均响应时间W与系统平均运行功率P进行归一化处理,构造无量纲系统成本函数如下。 其中,f1表示任务平均响应时间对系统成本函数的影响因子,f2表示系统平均功率对系统成本函数的影响因子[10]。当任务分配到移动设备本地的概率q的取值在[0,0.9]时,任务平均响应时间W的最大值和最小值表示为Wmax和Wmin,系统平均运行功率P的最大值和最小值表示为Pmax和Pmin。 为了实现系统成本函数的最小化,利用智能寻优算法找出最优任务分配到移动设备本地的概率。相比于一般的优化算法,鲸鱼优化算法的收敛速度较快,能够在较短的时间内寻找到目标函数的最优解。算法中的每一头鲸鱼所处的位置代表目标函数的一个可行解,采用随机和最佳搜索代理模拟鲸鱼的捕猎行为,并使用螺旋模型模拟座头鲸的汽泡网攻击机制[11]。本文中,增加了混沌初始化用来提高鲸鱼优化算法的全局搜索能力。算法的主要步骤如下所示。 步骤1初始化算法执行的最大迭代次数Maxiter=10 000,鲸鱼种群规模N=1000;设置任务分配到移动设备本地的概率q的上限qup=1 及下限qlow=0,当前迭代次数iter=1。 步骤2利用混沌方程初始化鲸鱼种群的位置。 步骤3设第1 条鲸鱼位置为当前最优位置q*,利用式(30)计算系统成本函数F(q*)。 步骤4利用式(30)计算全部鲸鱼所对应的系统成本函数F(qi(iter)),i=1,2,…,N,找出当前最优鲸鱼位置q*。 步骤5根据鲸鱼捕食行为更新鲸鱼位置。 步骤6判断迭代过程是否完成。 步骤7输出最优鲸鱼位置为最优分配到移动设备本地的概率q*,给出最小系统成本函F(q*)。 设置系统成本函数的影响因子f1=2.0、f2=1.6,利用改进的鲸鱼优化算法给出不同任务到达率下任务分配到移动设备本地的最优概率,优化结果如表2 所示。 表2 任务分配到移动设备本地的概率的优化结果 从表2 的数值结果可以看出,任务分配到移动设备本地的最优概率随着任务到达率的增大逐渐减小。移动设备的本地处理能力有限,随着任务到达率的增大,移动设备本地的任务量负载加重,因此,任务分配到本地执行的最优概率呈下降趋势。 综合考虑云用户的响应性能与云系统的能耗水平,在远程云端引入周期性休眠机制,提出了一种云计算任务调度策略。基于远程云端,考虑异构物理机,建立同步多重休假M/M/ck排队模型,给出了系统模型的稳态分布。基于Matlab 进行了系统实验,实验结果表明,任务平均响应时间与系统平均运行功率之间存在折衷关系。设定任务平均响应时间和系统平均运行功率的影响因子,构建了系统成本函数。利用混沌方程初始化种群位置,改进鲸鱼优化算法,给出了任务分配到移动设备本地的概率的优化结果,实现了系统成本函数的最小化。






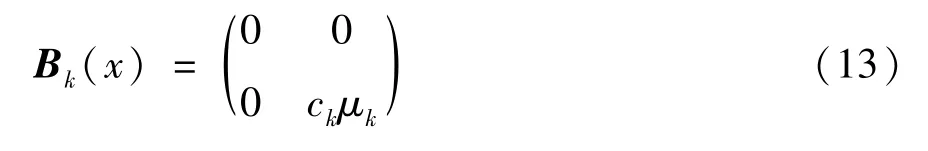
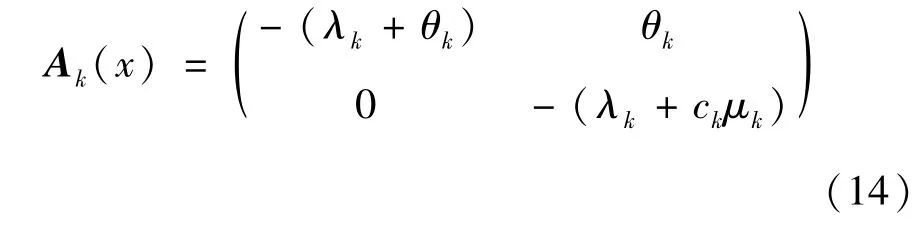








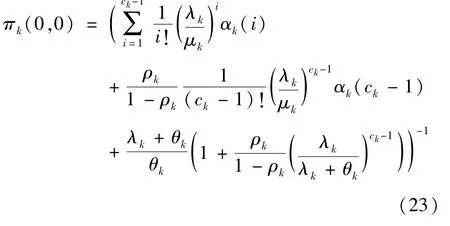
3 系统性能指标


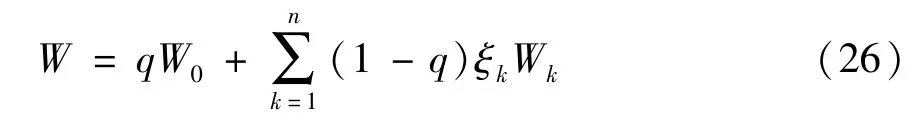

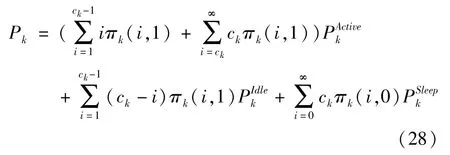
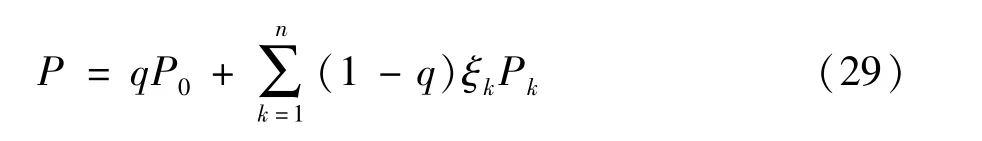
4 系统实验

5 系统优化





6 结论
