水下等离子体声源的电声转换模型研究与计算①
2021-11-14刘小龙雷开卓李洪兵
刘小龙 李 宁 雷开卓* 李洪兵
(*空军工程大学防空反导学院 西安710051)
(**中国船舶及海洋工程设计研究院 上海200011)
(***西北工业大学航海学院 西安710072)
0 引言
水下等离子体声源利用液电效应产生高强度的水下冲击波,该技术经过半个多世纪的发展,目前已经广泛应用于工业、医疗和国防领域等诸多方面,例如用于体外冲击波碎石、管道解堵、水处理、海底地质勘探与目标探测等。
水下等离子体声源电声转换的一般过程可以描述为:将交流电整流后对高压脉冲储能电容器充电,当达到预定电压后,击穿触发隔离间隙开关,使置于水中的放电电极两端瞬间加上高压,电极间的水介质在强电场作用下发生击穿,电能浪涌式释放并形成等离子体导电通道,发生水下脉冲放电。由于放电时间极短(几微秒),放电电流很高(千安到万安的量级),等离子体通道在极短的时间内获得大量的能量,通道内温度急剧升高,通道会受热体积膨胀。由于液体的不可压缩性和惯性,通道的膨胀受到阻碍,从而就会在水中形成巨大的冲击波,并逐渐衰减成声波,同时还伴随有光辐射和电磁波辐射等复杂物理现象。这种“液电效应”通常有两种基本形式[1],即电弧放电和电晕放电,本文仅限于讨论电弧放电形式的电声转换模型。
由于水下等离子体脉冲放电过程的瞬时性和不易观测性,对于该技术的电声转换研究尚无比较成熟的理论模型。大多数文献都是以应用研究为背景,从某个侧面对水下脉冲放电过程中的电特性或声特性进行研究,并利用经验公式或通过实验研究对比,给出冲击波性能与电路参数的定性关系[2-8],但尚未深入研究等离子体放电通道的电声转换效率问题。文献[5]结合实验测量波形和压力波计算经验公式获取放电回路参数和声波能量,并与理想情况下的电极注入能量相比来计算声效率。文献[6]给出了声效率的计算模型,但对于储能能量、系统输入能量、负载消耗能量等电路参数均是基于实验测量所得,并未给出放电电压、电流和冲击波等波形参数的数学表达式。文献[7]通过大量实验重点研究了水下电晕放电的电特性、声特性及其电参数对声特性的影响规律,给出了功率脉宽和直达波脉宽的关系。文献[8]在将电弧放电通道等效电阻视为时变电阻时,利用有限差分方法对放电回路的电流和电压进行了仿真计算,该方法在盐水中计算放电通道电阻时较为精确。本文基于典型水下等离子体电弧放电的实验装置和电参数、声参数测量波形,较为全面地分析充放电回路的电特性、等离子体通道电声转换特性,给出了系统能量传输的简化理论模型,并对充电效率、放电效率及电声转换效率进行了完整的理论描述,最后结合实验数据验证所提模型的可靠性,为进一步研究设计水下等离子体声源提供参考。
1 水下等离子体电声转换装置
水下等离子体电声转换装置等效原理图如图1所示,包括调压器t1、升压器t2、整流器D和充电回路总电阻R1(包括回路限流电阻和回路寄生电阻等)。高压脉冲储能电容C,隔离间隙G,放电回路寄生电感L,放电回路总电阻R2(包括放电电极放电时的电阻),以及放电电极S。整个装置可以分成两大部分:(1)充电回路,如图1 中实线框部分;(2)放电回路,虚线框所示部分。其中U为交流电网供电电压,u0为交流电网的有效电压,u1为调压变压器输出,u2为升压变压器输出,iin(t) 为充电回路电流,io(t) 为放电回路电流。
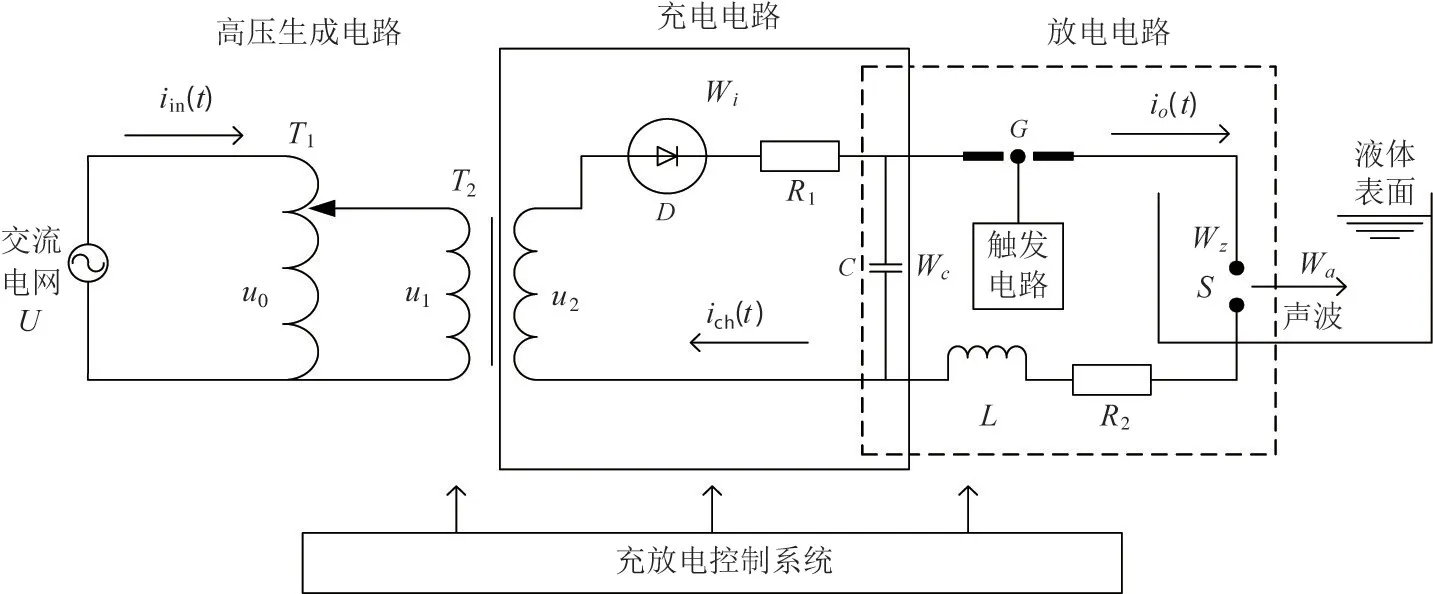
图1 水下等离子体声源装置原理图

由于水下等离子体声源具有可重复性,对于充电回路而言,要求尽量在短时间内对储能电容进行大容量充电,并减少充电回路的热损耗,因此充电回路采用高效率、低内阻的高压生成电路;对于放电回路而言,储能电容需要在极短的时间内将存储能量释放给放电电极,因此通常选用电容容量大、耐压高、损耗低、寄生感抗低的高压脉冲储能电容,并要求放电回路中的传输线缆电感和放电电极电感尽量小,以此来提高放电效率。
2 水下等离子体电声转换模型
充电回路前边的电路部分,即交流电网⇒调压器⇒升压变压器输入端,这部分的电能消耗可以使用电能表测得,本文并没有考虑这部分的能量消耗与关系,仅考虑升压变压器输出端之后电路系统的能量关系。
在研究电声转换模型时,为了便于分析,将整个系统划分为充电回路和放电回路,然后再分别对充电回路和放电回路的能量模型进行研究。
2.1 充电回路
充电回路如图1 中实线框所示,其回路方程可表示为
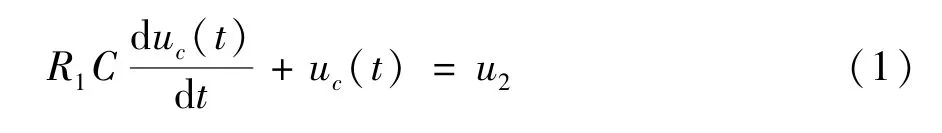
式中,u2为升压变压器输出电压,即充电电压。系统采用恒压充电,因此u2为常数。uc(t) 为高压脉冲储能电容两端的电压,R1为充电回路的总电阻。在充电回路部分,包括输入能量Wi和输出能量Wc两部分能量,下面分别给出其定义和计算表达式。
(1)输入能量Wi。其定义为升压变压器输出端⇒高压整流硅堆⇒充电至高压脉冲储能电容器,这几个阶段所消耗的电能。Wi可以通过对充电回路的电压和电流进行测量,再对其乘积进行积分得到,即
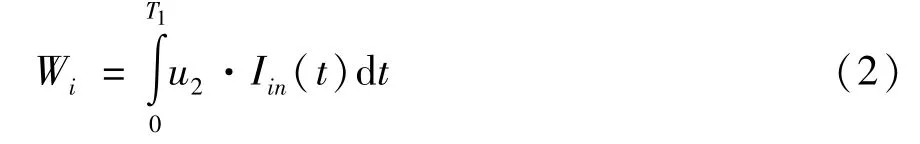
其中,T1为充电时间,Iin(t) 为充电回路电流,且根据式(1)有:
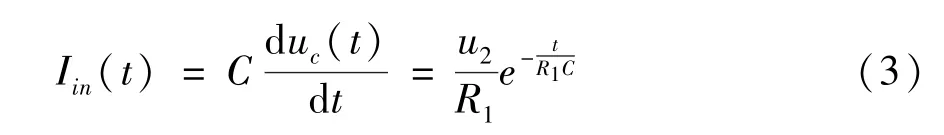
将式(3)带入式(2),得出输入能量的表达式为
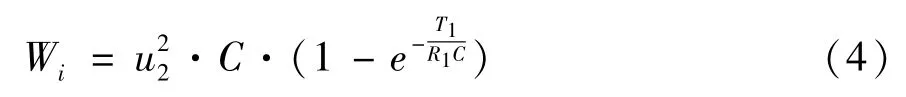
(2)储能能量Wc。其定义为充电回路输出给高压脉冲储能电容的能量,即为高压脉冲储能电容器储存的能量。
根据式(1)可以求出高压脉冲储能电容两端的电压为
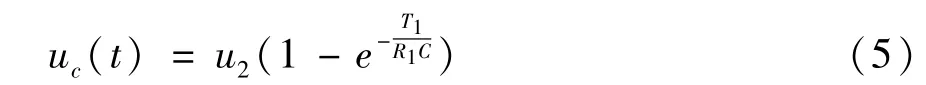
当t=4R1C时,即充电时间T1=4R1C时,高压脉冲储能电容两端电压uc=0.98u2,此时一般认为充电已经结束[9]。因此,储能高压脉冲储能电容器的储存能量Wc为
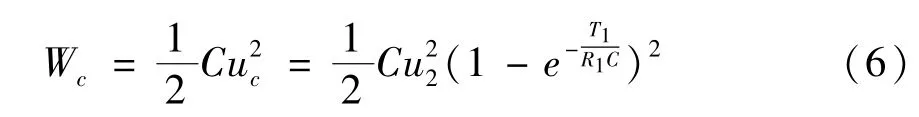
在一定的误差范围内,也可以近似地利用Wc=计算。
2.2 放电回路
(1)负载消耗能量Wz。其定义为当放电回路中的触发开关导通后,瞬间加载到放电电极两端的能量。
图2 是在高压脉冲储能电容为5 μF、放电电压为16 kV、放电电极间隙为4 mm 时测得的放电回路电流和电压波形。可以看出,电压和电流的峰值并不出现在同一时间,这个现象是由于放电回路存在寄生电感引起的。在本次讨论中,并没有考虑放电等离子体通道电阻的电感成分,而是假设放电通道电阻是纯电阻,这样的假设并不是没有根据的[10]。为方便模型的建立和计算,将电流和电压的波形用一个包络为指数衰减的sin 函数来逼近,分别由式(7)和式(8)表示。
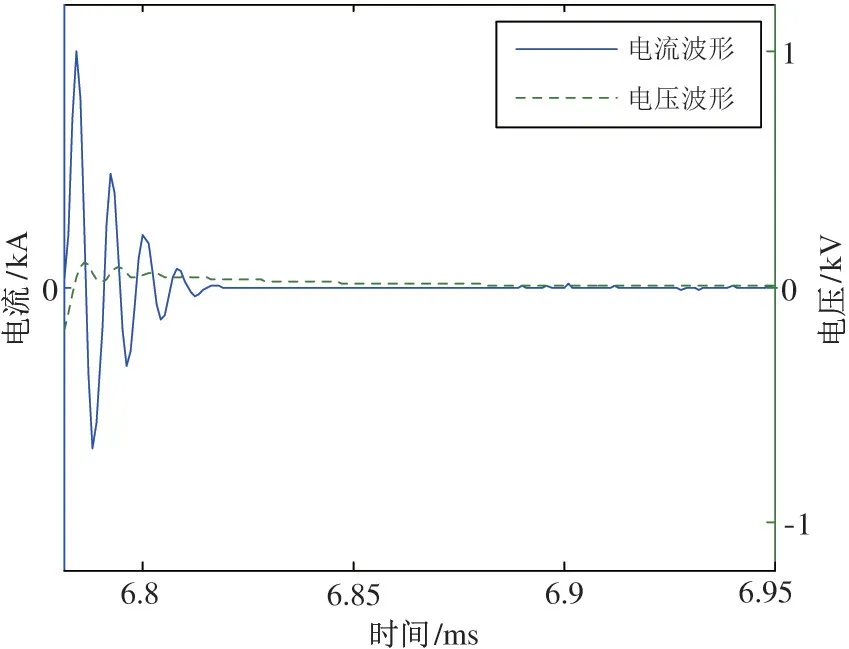
图2 放电回路典型的电压、电流波形
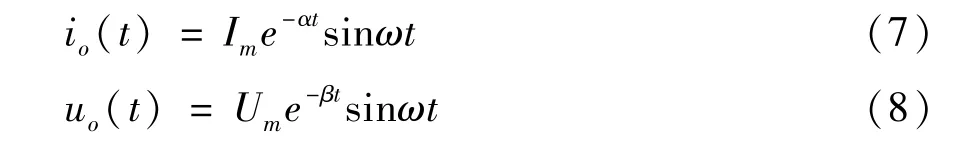
式中,Um和Im分别为电压和电流的最大值,α和β分别控制电流和电压的衰减快慢,ω为振荡频率。这5 个量可以在电压和电流的波形中得到,进而可以计算得到负载消耗的电功率。由于本文将放电回路的电阻看作是纯电阻的,因此可将电流和电压表达式中的ω视为相等。电功率可表示为式(9)的形式。
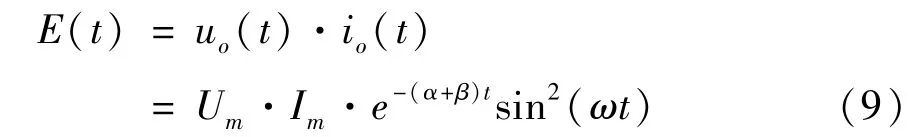
其中,E(t) 为电功率。则负载消耗的能量为

其中,T2为放电时间,可选取能量集中的前3~4 个周期为计算时间。
(2)声能量Wa。其定义为水下等离子体电弧放电过程中,等离子体放电通道膨胀后所产生的强声冲击波的能量。
水下等离子体声源产生的冲击波能量可根据声信号压力分布曲线求得,当传播距离超过声源半径10~20 倍的距离时,由冲击波引起的滞后流的影响可以忽略不计[11-12]。水下等离子体声源的半径近似等于放电电极间隙,一般电极间隙设置为1~4 mm,因此满足上述近似条件,则Wa可由式(11)求得。
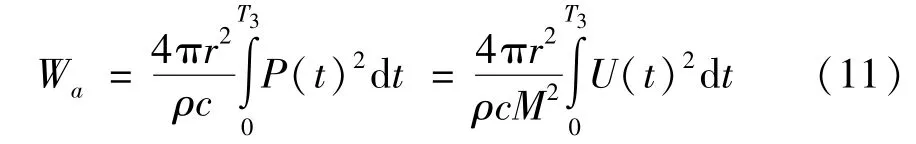
其中,r为测量点到声源的距离,ρ为水的密度,c为声速,M为传感器的灵敏度,T3为压力传感器输出信号的脉宽,P(t) 为声压,U(t) 为传感器输出电压信号。
图3 是通过实验在不同放电电压下测得的由压力传感器输出的电压信号典型波形。其中,高压脉冲储能电容的电容值为1 μF,放电电压分别为10.5 kV、5.5 kV 和7.6 kV,电极间距为1 mm。为了便于观察波形,将3 个压力传感器输出的电压信号波形放在一起,可以看出,不同放电电压下的传感器输出电压信号的波形重复性很好。由于水介质的阻尼作用,声波的强度呈指数衰减,因此电压信号的波形可以用式(12)来逼近,即
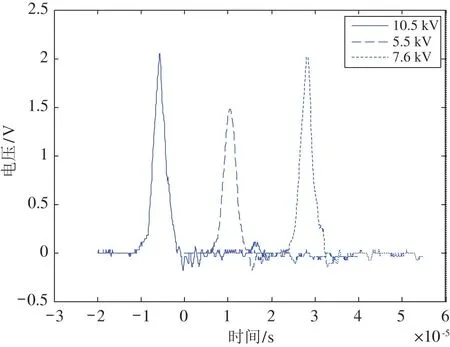
图3 压力传感器测得的电压信号典型图形
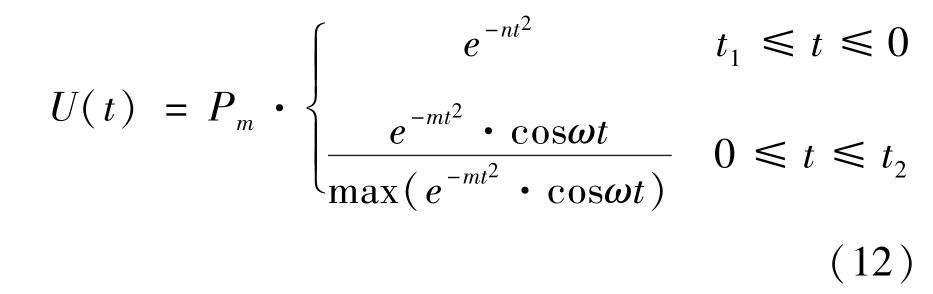
式中,m、n根据测得的实际电压信号波形拟合来选定,max(e-mt2·cosωt) 表示求e-mt2·cosωt的最大值。
2.3 不同效率的定义
通过上文分析,现给出系统各部分效率的定义及其计算表达式。
充电效率ηe定义为储能电容器的储能能量Wc与系统的输入能量Wi之比,表达式为
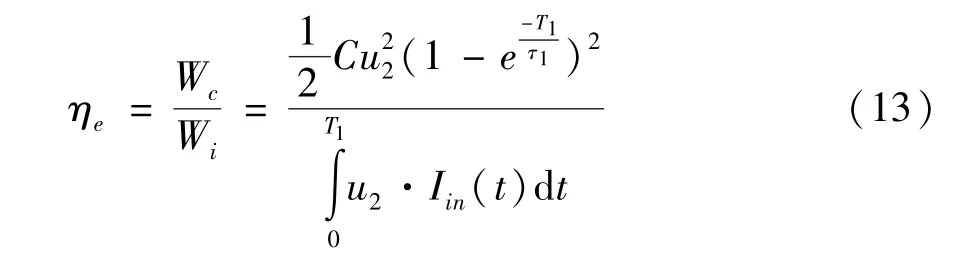
式(13)反映了升压变压器输出端⇒高压整流硅堆⇒充电至高压脉冲储能电容器这几个环节总的效率。
传输效率ηc定义为传输至负载放电电极所消耗的能量Wz与储能电容器的储能能量Wc之比,表达式为
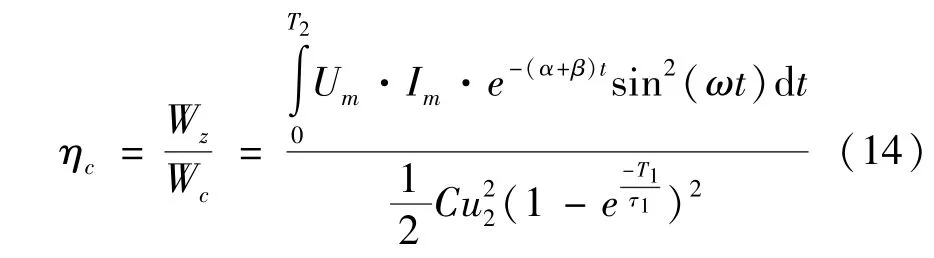
式(14)反映了高压脉冲储能电容能量实际传输到负载上的传输效率。因为高压脉冲储能电容的能量并没有完全加载到负载上,有一部分会消耗在传输线等中间部件上,如传输线、隔离间隙等,最后负载上释放的能量只是高压脉冲储能电容储存能量的一部分。
电声转换效率ηa定义为放电产生的强声冲击波能量Wa与负载放电电极消耗能量Wz之比,表达式为
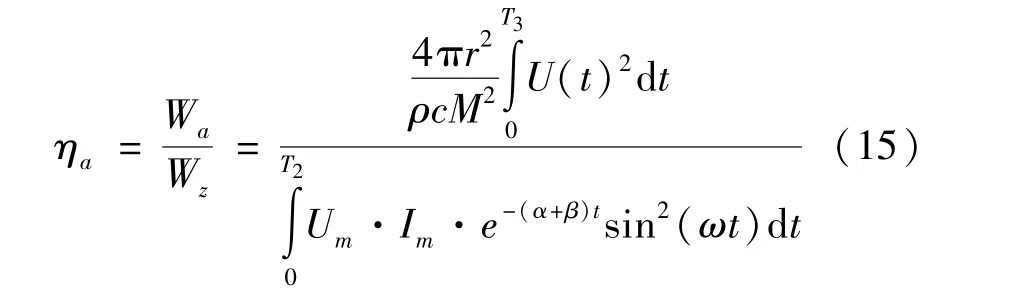
式(15)反映了加载到负载放电电极上的总能量通过电声转换后最终形成声能量的转换效率。
通过上述分析,系统总声效率ηS为各部分效率的乘积,表达式为

式(16)反映了等离子体声源系统最终产生的声能量与系统输入能量的比值。
3 计算结果与讨论
如前所述,本文建立了水下等离子体声源电声转换模型,并给出了系统各部分的能量和效率计算方法。下面利用水下等离子体声源实验装置开展声源系统电声参数测量实验,进而验证前面理论研究的有效性。本文利用图1 所示的水下等离子体电声转换实验装置开展实验研究,实验条件如下:实验水域3 m×1 m×1 m,箱体内注入自来水,放电电压为10 kV,放电电极间距为2 mm,储能电容为0.8 μF,压力传感器测量点距声源中心16.7 cm。在该实验条件下实际测得的传感器输出电压波形,即冲击波波形如图4 所示,图中实线部分为实验测量波形,虚线部分为利用式(12)仿真计算的拟合波形,由图4可以看出拟合出来的信号波形与实验测得的波形一致性很好,因此在计算水下等离子体声源产生的声能量时,利用拟合出来的波形能较好地反映实际情况。
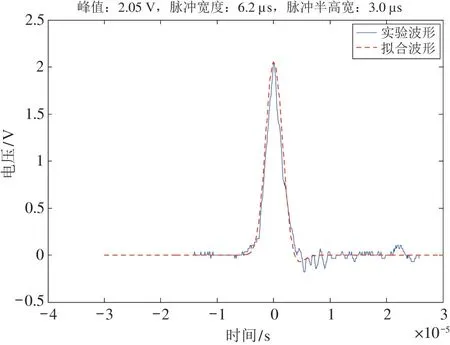
图4 冲击波实验波形与拟合波形
图5 是根据式(7)和式(8)得到的放电电流和电压的波形。其中,放电电压波形是虚线部分,放电电流波形是实线部分。对比图5 与图2 可以看出,计算模型中所用的电流和电压的函数波形能够较好地保持实际实验测得的波形的主要特性(幅度、衰减、振荡频率等)。在放电通道形成之前,放电电极间的电压等于储能电容两端的电压,这时由于并没有形成等离子体放电通道,因此没有电流流过放电电极,放电回路电流为0。由图5 与图2 均可以看出,放电电压和放电电流的峰值相差半个周期。
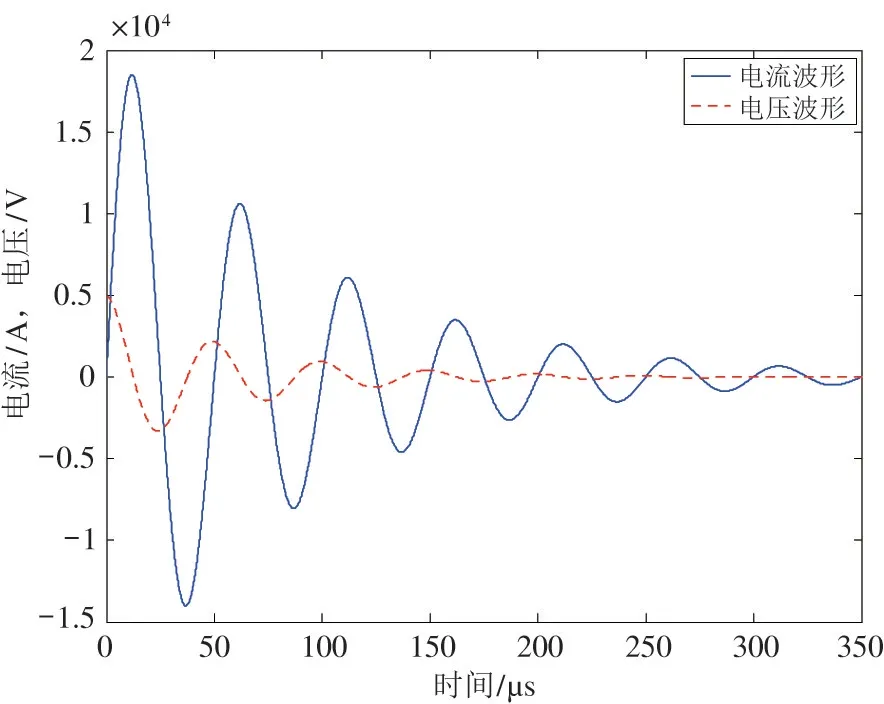
图5 计算得到的放电电流与电压波形
图6 是利用模型计算得到的放电功率随时间的变化曲线。由于放电电流与放电电压的峰值出现时刻相差半个周期,因此,放电电功率的振荡频率为放电电压(电流)的2 倍。并且在开始的前3 个周期,电功率的衰减并不太大,随后衰减逐渐增大。因此,在计算放电电能的时候,可以选取电功率较大的前4~5 个周期。
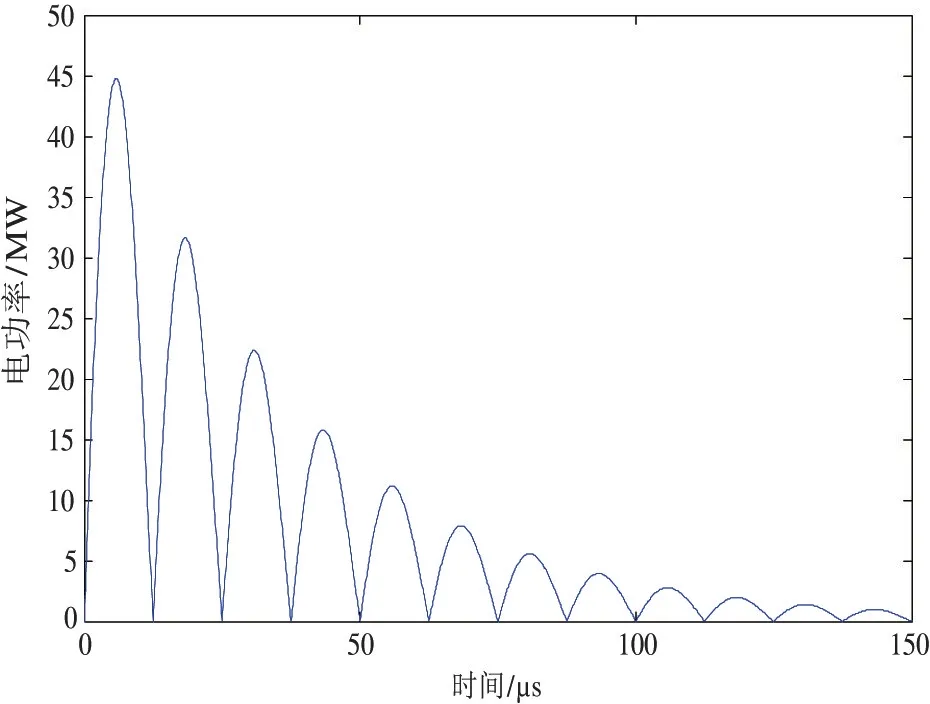
图6 电功率随时间的变化曲线
通过上述分析,在相同实验条件下,当充电时间为4τ,利用压力传感器在距放电电极中心16.7 cm处测得的冲击波电压峰值为2.05 V,90%脉宽为6.2 μs,如图4 中实线所示。
当压力传感器电压和声压的转换系数为1.4 MPa/V,放电电流的峰值约为4000 A,电极两端的电压约为3000 V 时,通过式(6)计算得到的电容器储存能量为Wc=38.55 J,负载消耗的能量由式(7)~(10)计算得到,即
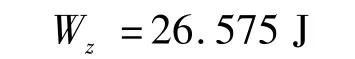
传输效率根据式(14)可以计算得到,即
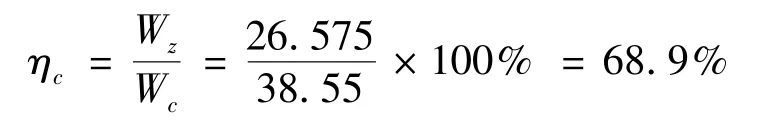
利用上述实验系统形成冲击波的声能量可根据式(11)、式(12)计算得到:
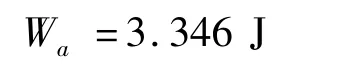
电声转换效率为
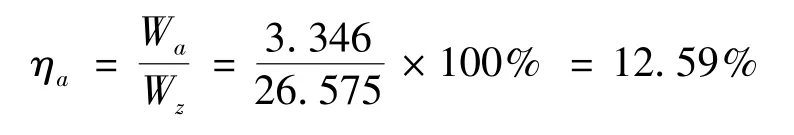
充电效率根据式(13)可得:
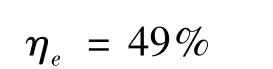
则系统总效率为
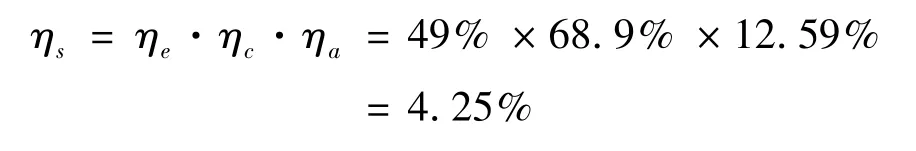
4 结论
本文详细分析了水下等离子体声源电声转换装置的电特性,并对系统中各部分能量和效率进行了定义,在此基础上,建立了水下等离子体声源的电声转换效率模型和系统总效率模型。结合等离子体声源电声转换实验装置,利用所建立的电声转换效率模型,对系统中的能量消耗、传输及系统效率进行了计算。由于本系统采用恒压充电方式,根据式(13)可知系统的充电效率最高为50%,效率较低。如果采用恒流充电可以将效率再提高40%左右。通过计算得出系统总效率在4%左右,与其他文献给出等离子体电弧放电系统的总效率在一个量级上。如果要提高系统总效率,可对高压脉冲储能电容、系统储能、放电电极结构、放电电极间距、系统充电方式、馈线方式等不同充放电回路参数进行合理设计,如减小放电回路的寄生电感、采用“最佳放电电极间距”等,进而达到对冲击波波形参数的设计,提高电声转换效率,最终达到提升系统总效率的目的。
