一种紧凑型1024点流水线FFT处理器设计
2021-11-14霍永华焦利彬
于 建,霍永华,焦利彬,杨 杨
(1.河北民族师范学院 物理与电子工程学院,河北 承德 067000;2.中国电子科技集团公司第五十四研究所, 河北 石家庄 050081;3.北京邮电大学, 北京 100876)
0 引言
快速傅里叶变换(Fast Fourier Transform,FFT)是基于正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)传输方式通信系统中的关键性技术,用于传输数据在时域与频域之间的转化[1]。OFDM作为使用最广泛的多载波调制技术,已成为多种通信领域的规范基础[2],如长期演进(Long Term Evolution,LTE)、无线局域网(Wireless Local Area Network,WLAN)以及全球微波互联接入(Worldwide Interoperability Microwave Access,WiMAX)等[3],同时,OFDM在5G通信系统中仍然是最为主要的调制技术[4]。在OFDM系统中的物理层,FFT处理器是最为复杂的运算模块,消耗大量的硬件资源[5],因此大量的研究都聚焦于FFT算法与硬件实现架构的优化,达到降低其所消耗的硬件成本。
算法方面,基-2库里图基FFT 算法最为著名[6-7],它拥有简单的蝶形单元,非常适合硬件的实现,但所需的复数乘法运算量大。基-2kFFT算法[8]解决了基-2算法复数乘法运算量过大的问题,同时还能够保持与基-2算法一样简单的蝶形单元,因此非常适合用于FFT处理器的硬件实现。基-2k算法根据k值的不同可分为基-22算法、基-23算法、基-24算法和基-25算法等。
硬件实现架构方面,由于流水线架构(Pipelined Architecture,PA)[9]具有适中的硬件资源消耗与更高的数据吞吐量,常被用于FFT处理器的硬件实现。PA架构又分为前向反馈与负反馈2种风格[10],由于负反馈风格中的SDF架构需要更少的寄存器以及更简单的控制逻辑,常被用于低硬件成本FFT处理器的设计。

1 算法选择与评估
考虑到基-2k算法不但拥有与基-2算法一样简单的蝶形架构,还能够减少旋转因子的运算复杂度,因此本文采用基-2k算法用于1 024点FFT处理器的设计。
不同k值的基-2k算法针对1 024点FFT计算一共包含9个旋转因子计算阶段,只是k值的不同会导致旋转因子不同。表1所示为不同k值的基-2k算法在计算1 024点FFT时旋转因子的详细分布情况。

表1 1024点基-2k算法旋转因子运算分布Tab.1 Distribution of twiddle factor at each stage to compute 1024-point FFT for radix-2k algorithm

2 整体设计方案
图1所示为基-25算法SDF架构1 024点FFT处理器的整体结构图。图1中,BF2I与BF2II模块为基本的I型与II型蝶形单元,主要用于输入复数序列的加法与减法运算,II型蝶形单元除了进行基本的加减法运算还要处理额外的‘-j’运算[14];蝶形单元上方的矩形块为不同容量的延迟缓冲单元,主要为蝶形单元的输入提供恰当的数据并对数据进行整理;‘⊗’代表复数乘法运算单元,输入序列通过复数乘法单元运算后,就会得到与相应阶段旋转因子相乘的结果,计算后的结果会直接进入下一阶段的蝶形运算中;‘CLK’为控制时钟,由10位计数器产生,用于切换蝶形单元的类型并为复数乘法单元提供合适的控制逻辑。

图1 基-25算法1024点SDF FFT结构图Fig.1 Block diagram of radix-25 1024-point SDF FFT
2.1 旋转因子拆分与两阶段CSD常数乘法

2.1.1 旋转因子拆分原理
图2所示为截取基-25算法64点FFT第5阶段旋转因子运算的信号流图。


图2 第5阶段基-25算法64点FFT信号流图Fig.2 SFG of radix-25 for 64-point FFT of the 5th stage

逻辑模块

(b) 改良后的蝶形单元图3 内嵌模块的蝶形单元Fig.3 Butterfly unit with embedded
2.1.2 两阶段CSD常数乘法单元


表2 8区域中旋转因子对应的映射Tab.2 Eight symmetric region mapping of twiddle factor
(1)
CSE1=din+din>>2
CSE2=din-din>>2
CSE3=din+din>>3
CSE4=din-din>>3
CSE5=din-din>>4。
(2)

表3 12位字长16组常数值CSD数值表示Tab.3 CSD representation of sixteen constant values with 12-bit word-length
2.2 适配于与乘法单元
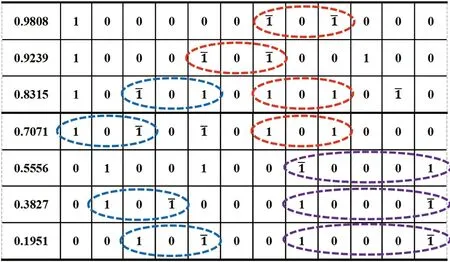
表4 7常数值CSD表示Tab.4 CSD representation of seven constant values
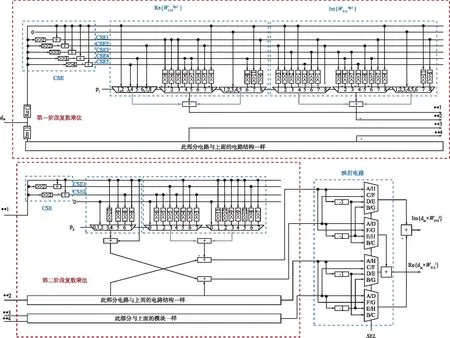
(a) 适配于旋转因子两阶段CSD常数乘法单元逻辑模块

(b) 两阶段复数乘法及控制逻辑图解图4 适配于旋转因子两阶段CSD乘法单元整体架构详解Fig.4 Detailed overall architecture of two-stage CSD multiplied unit for twiddle factor

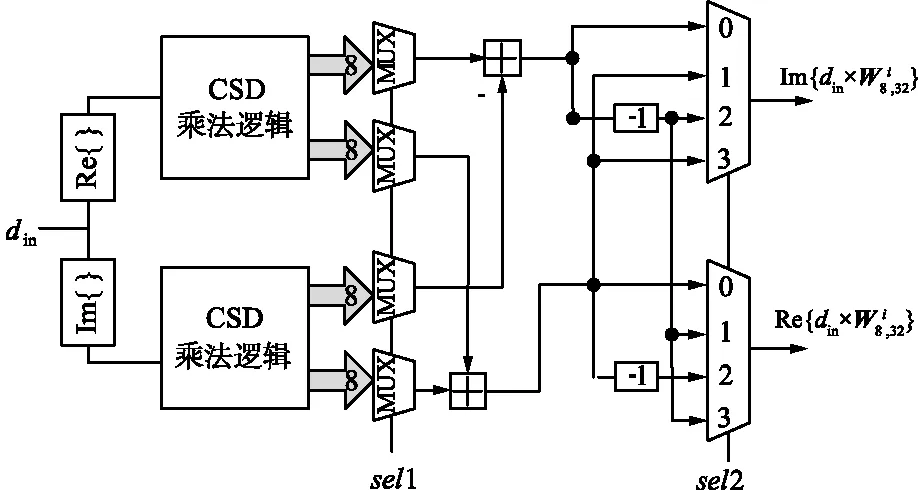
(a) CSD常数乘法单元通用架构

(b) 适配于与逻辑模块图与乘法单元Fig.5 CSD multiplied unit for
3 评估与比较
采用Verilog HDL对所设计的1 024点FFT处理器进行建模,利用QUARTUS PRIME开发平台对设计进行综合评估,器件选择Intel FPGA CYCLONE家族的10CL055YU484I7G。表5所示为本文的设计方案与其他已存在的设计方案在1 024点FFT处理器设计方面的比较,为了更加直观地评估各个方案的硬件资源消耗,对设计所消耗的LEs与MBs进行了标准化处理,设定本文方案的所消耗的LEs与MBs为1。
图6所示为基于Matlab计算出的结果与QUARTUS PRIME平台仿真工具MODELSIM-ALTERA得出结果之间的比较(设输入序列的实部与虚部取值范围为1~1 024),其中‘*’代表Matlab计算结果,‘△’代表MOELSIM仿真结果。
图6中FFT点数的输出结果表明,MODELSIM仿真结果与Matlab计算结果完全吻合,验证了所提出设计方案的有效性。

(a) 计算结果比较(FFT点数取值范围0~50)
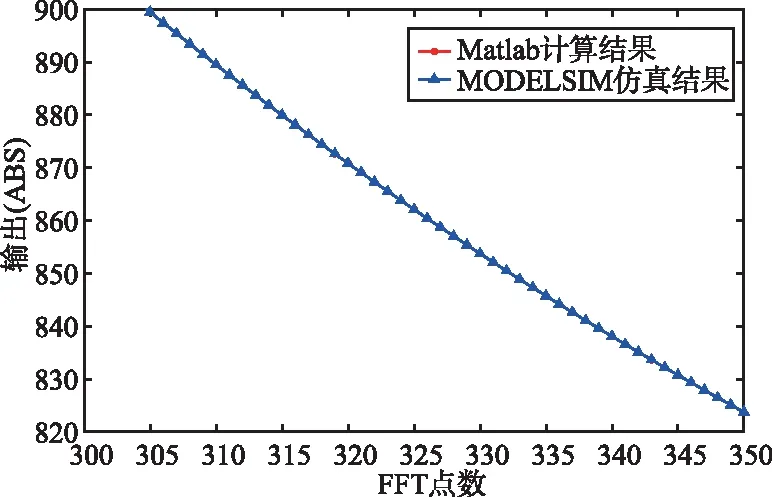
(b) 计算结果比较(FFT点数:取值范围300~350)
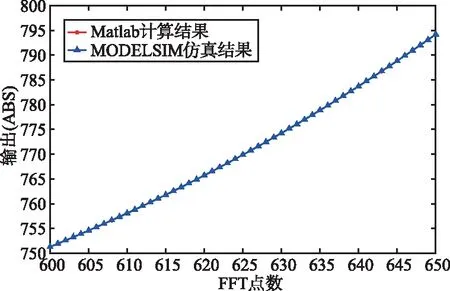
(c) 计算结果比较(FFT点数:取值范围600~650)
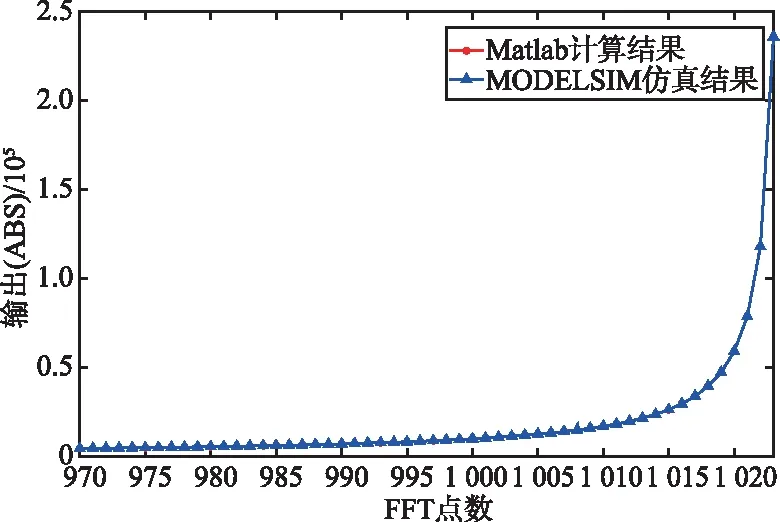
(d) 计算结果比较(FFT点数:取值范围970~1 023)图6 MODELSIM结果与Matlab计算结果比较Fig.6 Comparison between MODELSIM simulation result and Matlab calculation result
由表5可知,对比已存在的设计方案,本文的设计方案至少能够节约28%的LEs与48%的MBs,工作频率为120 MHz时功耗为12.6 mW。本文的设计方案内部字长设定为24 bit,SQNR达到了57.6 dB,同时本文无需布斯乘法器参与复数乘法运算,全部采用硬件资源消耗低的CSD常数乘法器来完成。

表5 不同方案1 024点FFT处理器性能比较Tab.5 Performance of the proposed 1 024-point FFT processoras compared with existing schemes
4 结束语
本文基于Intel FPGA设计了一种紧凑型1 024点FFT处理器,为了减少旋转因子的复杂度,采用了基-25算法,考虑到硬件实现的难易度和硬件成本问题,使用了SDF流水线架构。在此基础上提出了一种旋转因子的分解方案,使得所有复数乘法运算全部由CSD常数乘法单元完成,大幅度地降低了硬件成本。基于QUARTUS PRIME综合结果显示,对比已有的方案能够至少节约28%LEs和48%MBs的使用量,SQNR达到了57.6 dB,工作频率为120 MHz时,功耗为12.6 mW,本文所设计的1 024点FFT处理器非常适合对硬件成本和功耗要求苛刻的应用场景。
