舰船短波信号快速测向技术研究及仿真

陈 静

(中国人民解放军91404部队，河北 秦皇岛 066001)

0 引言

空间谱算法在20世纪60年代被提出，目前为止应用较为广泛的一种空间谱估计算法[1]是多重信号分类算法。在空间谱算法的基础上提出了大量的子空间分解类算法，按照算法方向可以将其分为噪声子空间以及信号子空间2类[2]。许多估计算法在实际的工程应用耗时耗力，没有被广泛使用到实际测算中[3]。有学者遵循均匀圆阵多重信号分类算法在处理问题时数据之间的循环特性，将空间表达式进行等价变换，利用DFT算法来实现空间谱算法快速计算的目的。也有学者提出将求根多重信号分类算法中的求根计算利用线性搜索的计算方法来代替[4]。

在20世纪60年代，空间谱估计将干涉仪技术进行了引进，干涉仪技术是一种测向算法，主要含有相位干涉仪和相关干涉仪2类算法[5]。对不同阵元之间的相位差进行计算是相位干涉仪算法的显著特征，再通过阵元之间的空间位置关系利用比相的方式得到信号的入射方向[6]。系统的测向精度可以通过相位信息来对两阵元之间的距离进行调整得到，当处于一定范围内时，间距越大，测向精度也越高，一旦超出间距范围(阵元间距比半波长大)，会使其产生相位模糊的现象，从而使得测向精度和相位模糊二者矛盾[7]。相关干涉仪的测量依赖于实际测量得到的相位差数据和在不同方向下的相位差数据求得其相关度，对最大相关度匹配的方向进行搜索从而完成对来波的方向测算。相关干涉仪利用比较相关度的方式对相位模糊问题进行消除和减弱，由于该算法避免了相位模糊的问题，使其应用范围更广[8]。

本文通过一种基于快速卷积理论的空间谱算法来解决空间谱中的快速计算问题，然后提出了一种基于引导基线的相关干涉仪测向算法，解决舰船短波信号处理过程中计算量过大的问题。研究利用单信道瓦特森-瓦特算法和相关匹配提取示向角度值的方法对所提出的算法进行了仿真分析，最后对仿真结果进行分析总结。

1 无线电测向算法

1.1 基于快速卷积理论的空间谱算法

在短波测向中圆阵是一种最常见的阵列形式，在此基础上基于快速卷积理论结合多重空间分类算法的空间谱快速计算方法，这种算法相对来说测向时效性得到了提高[9]。实际生活中，空间谱的点数和圆阵的阵元数不一定相等，不能保证圆阵分布是均匀的，所以在进行空间谱的计算是无法直接利用方向向量和特征向量二者的循环卷积算法的。

为了对其进行计算，通常会利用构建虚拟圆阵的方式进行计算，将阵元数M变换为K，使其成为一个虚拟均匀圆阵，该阵元的输出结果为0。经过扩展后得到了一个阵元数K和空间谱点数L相等的阵列，此时就可以对构建虚拟均匀圆阵通过卷积的方式计算出该阵列的空间谱。所以，方向向量的表示方法为：

∂(θ)=[∂1(θ)，∂2(θ)，…，∂k(θ)]。

(1)

对于多重空间分类算法，同样需要调整噪声子空间中的元素分布，实现方式是将0元素按照一定的方式将其加入到相应的位置中。同时还要保证虚拟阵列的空间谱计算结果和原始阵列的计算结果一致，所以引入的0元素和原特征向量各元素的位置关系要和阵元扩展后阵列中虚拟阵元与真实阵元之间的位置关系一致[10]。因此得到的利用虚拟阵列计算多重空间分类算法倒谱的计算式为：

(2)

在仰角一定的时候，B中的第n行向量ψ可以通过第1行向量a对各分量进行n-1次循环移动得到。

由于阵元数和空间谱点数相等，所以多重空间分类算法倒谱的计算可以通过方向向量和特征向量进行卷积计算得到。卷积计算可以通过离散傅里叶计算得到，当空间谱点数为2的n次方时，离散傅里叶可通过快速傅里叶变化得到[11]，所以，当仰角为ψ时，多重空间分类算法倒谱的计算方式为：

(3)

(4)

式中，round( )指的是要将( )内的结果进行四舍五入，映射误差是通过K值来决定的，二者之间是反比例函数。通过阵列的最大相位差来对K进行取值时，其应该处于阵列所能容许的最大误差范围之内。误差的计算表达式为：

(5)

式中，Δεmax是阵元的最大角度映射误差，通过具体的阵行进行确定。在实际的应用过程中，要想获得更高的测向时效性，K值并不一定要按照上述要求选择，可以取更小的值。阵元位置的映射误差也会造成测向结果的偏差，此时在与测向结果比较近的范围内对其再进行比较细致的谱峰搜索，可以提高测向的准确度，消除因误差造成的测向偏差。

1.2 相关干涉仪测向算法

在计算时，相关干涉仪技术中的三角函数计算是一个耗时的过程，为了减少该过程的耗时和复杂度，传统的方法是首先建立一个相位差的数据模版，该模版是全空域和全频段的。但是因为数据模版具有一定的离散性，该离散性主要表现在频率和角度上。这些因素会导致模版中的信号频率、角度不能保证与真实的数据值完全匹配[12]。为了减小该影响，就要在生成的数据模版中，其步进越小离散性也会越小，但是在减小数据模版步进的同时会增大测向系统的存储资源成本。

计算相关度的时候，基于基线引导的相关干涉仪算法也需要对相位差的数据模版进行设计。为避免传统算法的弊端，还需要解决角度和频率匹配度和内存资源占用度之间的矛盾。基于基线引导的相关干涉仪算法实时依据工作频率与搜索角度进行计算，可减少事先建立好数据模版的步骤[13]。

与传统的计算方式相比，利用基于基线引导的相关干涉仪算法实时计算模版数据的方式会导致有额外的计算量产生，为了避免该影响，需要对数据模版的算法进行优化。优化方法是将与相关度计算中的相位差对应的两阵元坐标分别设为(x1,y2)与(x2,y2)，且当信号的入射角一定时，可以得到相位差的模版数据：

ji(fmn,qmn) =v1(j1+2pm)+v2(j2+2pn)。

(6)

相关度的代价函数为：

(φ,θ) = argmax(φmn,θmn)。

(7)

将式(6)代入式(7)可以计算出角度的相关度，且在阵形确定的情况下，v1，v2都是常数。利用优化后的算法确定了算法的搜索范围，降低了算法的复杂度，提高算法计算效率的同时也提高了计算精度。

1.3 单信道瓦特森-瓦特测向算法

瓦特森—瓦特测向算法不是直接对来波的相位比较，而是将其转变为电压振幅之间的比较，以此计算出所要测量的来波示向度[14]。在理想状况下，该测向体制的方位感应电动势灵敏度可以通过正北方间的夹角余弦值的变化来确定，垂直方向的感应电动势的灵敏度则可以通过仰角的余弦值变化得到。

来波入射为任意方向时，北、南方向的电动势用VN/S表示，东、西方向的电动势用VE/W表示，来波的方位计算方式为：

(8)

来自θ与180°+θ角的电波，北/南和东/西天线上产生的电动势值一样。为了排除方位不确定的模糊性，在测向系统中引入一根判定天线。该判定天线是全向天线。将判定天线输出与另外二组天线的输出的相位差进行比较，可解决方位的模糊性。

该测向体系的显著特点是能够对同信道的干扰进行分辨，同时测向的时效性和准确度以及测向速率都比较高。由于该系统是小基础测向系统天线，所以天线的测向灵敏度以及抗波前失真会受到一定的限制。与多信道测向系统相比，单信道测向系统有着更为简单的架构，所需要的成本也会得到降低[15]。所以本文主要是对舰船上的单信道瓦特森-瓦特测向技术进行研究。

单信道瓦特森-瓦特测向系统首先将判定天线接收到的信号振幅为O(φ)=Ae，将O乘以幅度加权系数w0再与北南天线和东西天线分别合路，获得4组输出信号：

(9)

(10)

式(9)和(10)包含了方位向4个象限的来波信号测量的信息。与入射方位角的信息进行结合利用相关匹配法计算就可以得到的入射波的方位角φ。

对测向天线的性能进行衡量是依据测向精度进行评价的。在实际的应用中，幅度相位和天线单元响应的不一致，以及阵元的位置误差和互耦等特性会导致阵列模型产生不同程度的误差；接收机接收信号幅值的稳定程度也可能导致系统示向角度产生随机误差[16]。同时相位不平衡和硬件设备等因素都可能导致示向角的误差产生。利用相关匹配法对方位角进行提取时增加了一个预校准过程，可以在一定程度上缓解由于半径波长比的增大以及相位的不平衡所带来的误差。

2 中短波测向系统研究

2.1 基于快速卷积理论的空间谱算法结果

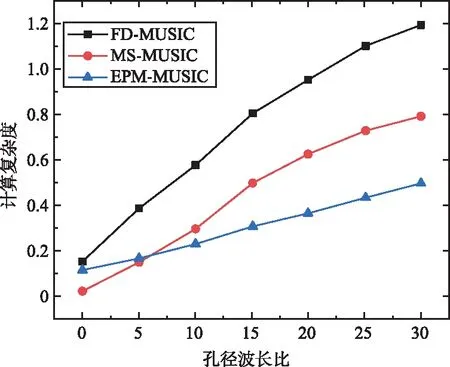
基于快速卷积理论的空间谱算法(EPM-MUSIC)可以适用于任何圆阵，为了验证该算法的复杂度和性能，对该算法、傅里叶域的多重空间分类算法(FD-MUSIC)和流形分离多重空间分类算法(MS-MUSIC)在任意阵、十字阵和均匀圆阵的情况下对其进行测试分析，分析结果如图1所示。图1(a)为任意阵下的不同算法的计算复杂度分析结果，图1(b)为基于十字阵的算法计算复杂度分对比结果，图1(c)为基于均匀圆阵的算法计算复杂度对比结果。

(a) 任意阵下的不同算法的计算复杂度分析结果

(b) 基于十字阵的算法计算复杂度分对比

(c) 基于均匀圆阵的算法计算复杂度对比图1 不同算法的计算复杂度分析结果Fig.1 Analysis results of computational complexity of different algorithms

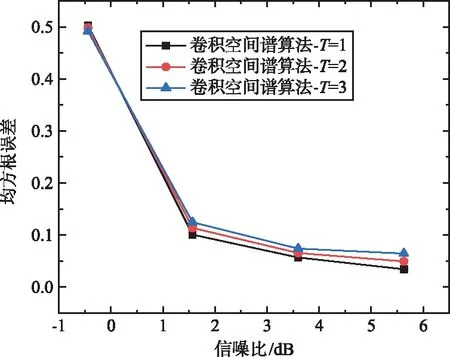
均方根误差与信噪比的关系曲线图如图2(a)所示，当T=1时的各算法测向性能对比图如图2(b)所示。

(a) 均方根误差与信噪比的关系曲线

(b) 当T=1时的各算法测向性能对比图2 不同算法的测向均方根误差结果分析Fig.2 Result analysis of direction-finding RMSE of different algorithms

由图1和图2可以看出，在不同阵形下的计算复杂度中，孔径波长比在变化时，EPM-MUSIC算法与FD-MUSIC算法和MS-MUSIC算法相比复杂度的变化不明显，所以，该算法具有较好的计算。EPM-MUSIC算法的计算复杂度要更有优势。而在测向性能对比中，几种算法的性能几乎一致，并没有太大的区别。

2.2 相关干涉仪的测向结果

为了验证本文提出的基于基线引导的相关干涉仪算法的测向性能。将其与基于余弦函数的相关干涉仪算法、伪线性迭代最小二乘测向算法进行测向性能对比。基于余弦函数的相关干涉仪算法的基线长度和测向性能相关，所以本文分别选择基线长度为短(S)、中(M)和长(L)三种类型进行测试，测试结果如图3所示。图3(a)为不同算法的方位角均方根误差对比图，图3(b)为不同算法的方位角解模糊概率对比图，图3(c)为不同孔径波长比的测向时效性分析结果图。

(a) 不同算法的方位角均方根误差对比

(b) 不同算法的方位角解模糊概率对比

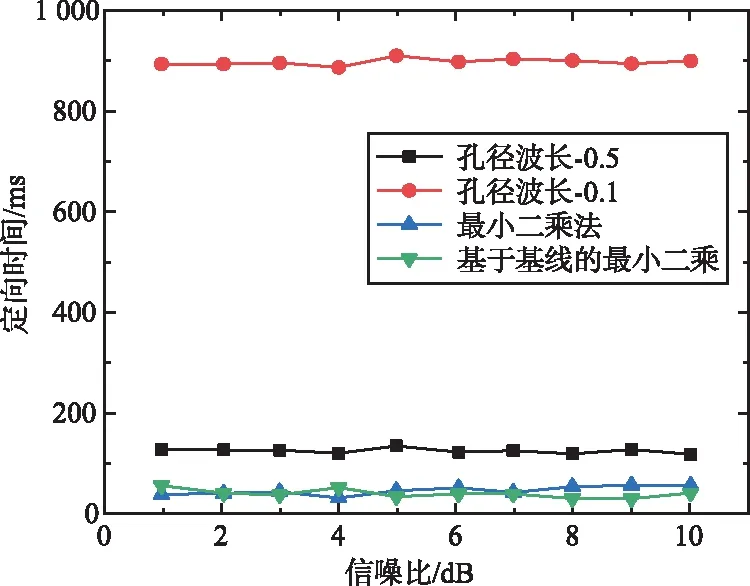
(c) 不同孔径波长比的测向时效性分析结果图3 不同相关干涉仪算法的测向性能对比结果Fig.3 Comparison results of direction-finding performance of different correlation interferometer algorithms

由图3可以看出，通过分析不同信噪比和不同孔径波长比下的测向性能，本文提出的基于基线引导的相关干涉仪算法的测向精度最高；合适的基线长度也会提高余弦函数法对伪相关峰的抑制效果。基于基线引导的相关干涉仪算法的测向时效性表现最好，占有较大的优势，更利于宽带信道化的测向处理。

2.3 单信道瓦特森-瓦特的测向性能分析

将相关匹配法和反正切算法进行对比测向性能，对单信道瓦特森-瓦特系统进行测试，测试结果如图4所示。

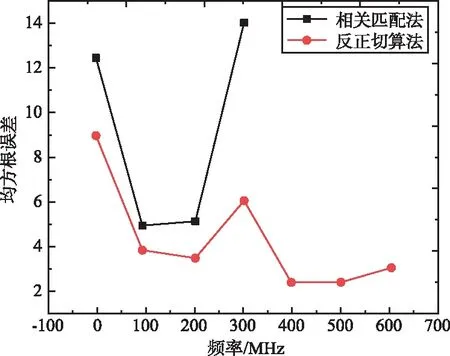
图4 不同算法的测向均方根误差对比结果分析Fig.4 Comparison result analysis of direction-finding RMSE of different algorithms

由图4可以看出，基于相关匹配法得到的均方根误差值整体要小于反正切计算法，得到的均方根误差都在10以内，可以满足小型化设备的性能设计要求。

3 结束语

针对短波测向的过程提出了一种基于快速卷积理论的空间谱算法，并利用基于引导基线的相关干涉算法对其进行优化，最后利用单信道瓦特森-瓦特算法和相关匹配提取示向角度值的方法进行了仿真研究，初步建立了舰船短波信号快速测向方法，很好地解决了目前舰船短波信号快速测向中常见的相位模糊的问题，可以简化工作流程。本文在研究时没有对电离层发生倾斜时的状况进行分析，而短波测向精度受电离层信道参数变化的影响非常严重，一旦当电离层出现大范围倾斜的情况，电磁波会发生传播路径偏移的现象，在这种情况下测向系统的测向结果是无法受到控制的，测向精度也无法保证，在后续的研究中将对不同电离层的倾斜状况进行分析，减小测向误差。