基于细长轴双密封阀芯的精密磨削工艺及应用研究
2021-11-13王熙杰
王熙杰

摘 要 为了对双密封结构阀芯的精密磨削质量稳定性进行研究,通过研究细长轴阀芯挤压变形磨削和形位精度系统模型,提出基于参考坐标系的阀芯精密磨削工艺方法,通过某型号批次应用取得了较好的效果,说明该工艺方法对提高细长轴双密封阀芯形位精度具有一定的理论和工程应用价值。
关键词 双密封阀芯 细长轴 形位精度 精密磨削
中圖分类号:TG58 文献标识码:A 文章编号:1007-0745(2021)10-0021-06
1 研究现状中存在的问题
双密封结构电磁阀是轨姿控发动机重要控制组件,为了满足客户某型号小型化的要求,该电磁阀采用单线圈、单阀芯结构对氧化剂路和燃料路同步控制,主要由基体、阀芯等组成。
双密封结构电磁阀一处为活门座非金属端面密封,另外一处为锥面非金属棱边密封。为了实现双密封同时密封成功,需要阀芯较高精度的形位公差,且阀芯双密封尺寸和基体的双密封尺寸具备高匹配性,否则就会导致双密封失败。问题主要有:(1)单阀芯双密封过程中对阀芯的形位公差要求均在0.01mm以内,而阀芯理论上为细长轴结构,加工过程中易受力变形,研制过程中阀芯形位公差合格率仅为60%;(2)合格的阀芯零件装入基体后,由于双密封尺寸匹配性较差,双重密封性难以保证,两处气密无法同时满足要求,只能通过不断返修阀芯上下密封端面保证密封性能,装配工艺性差,研制过程中气密合格率仅为30%。
2 细长轴双密封阀芯精密磨削研究现状及解决方案
解决单阀芯双密封结构电磁阀研制过程中存在的问题,保证阀芯磨削过程中形位公差并提高其气密合格率。双密封阀芯磨削属于成形磨削的一种,成形磨削是一种高效率、高精度的精加工方法,但是在磨削过程中不能完全消除加工误差。刘丰林等建立了磨削时的工件坐标系,提出了基于误差补偿的磨削砂轮截面算法,对误差进行控制[1]。康念辉等建立了基于多体系统理论的非球面磨削误差模型并对磨削误差进行补偿[2]。所以,对磨削成形过程中磨削误差的研究主要是根据工件形状和特点建立磨削误差模型或算法,形成误差补偿方法减小误差。
双密封结构电磁阀结构较为新颖,对双密封副尺寸匹配性的研究较少,研制过程中未对该阀门双密封副进行系统地理论研究,设计对双密封匹配尺寸也是基于研制过程中的工程经验而来。
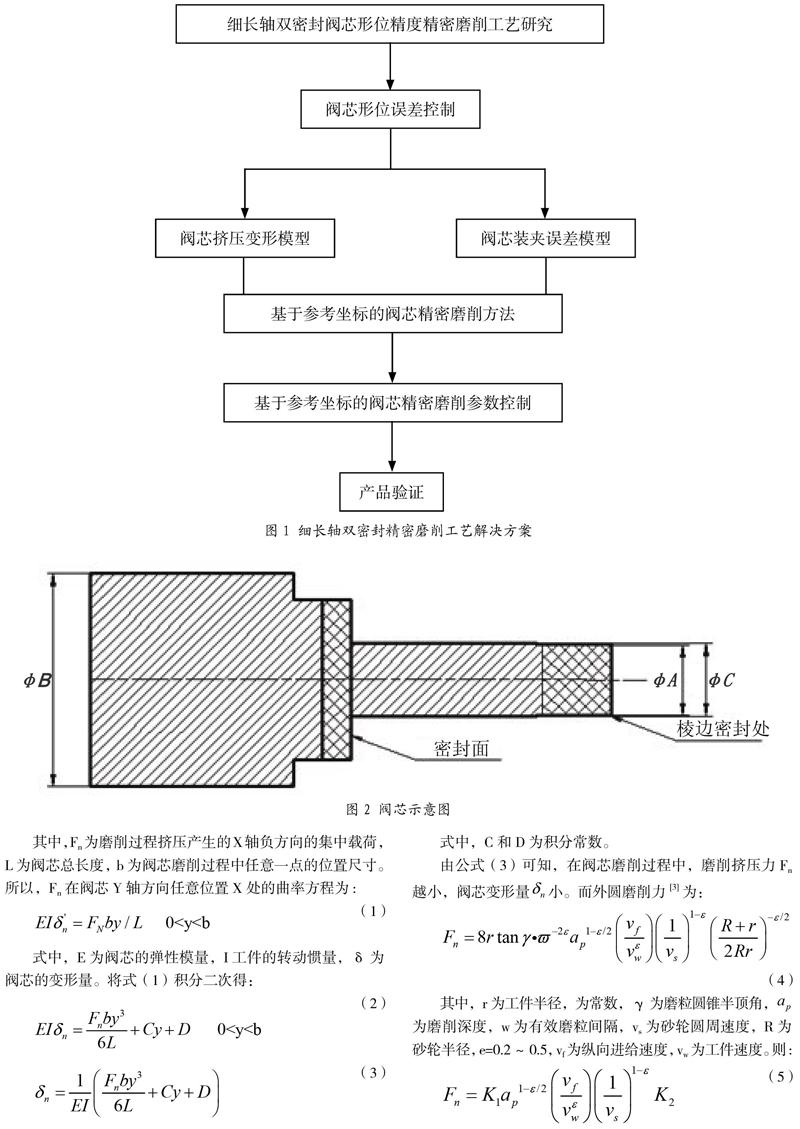
根据单阀芯双密封结构电磁阀研制中存在的问题及研究现状,本文对细长轴阀芯精密磨削质量稳定性进行研究,提出基于参考坐标的阀芯磨削控制参数,解决阀芯磨削过程中变形和形位关键尺寸超差的问题,为控制密封尺寸提供基础(细长轴双密封精密磨削工艺解决方案如图1所示)。
3 细长轴阀芯精密磨削稳定性研究
双密封结构电磁阀阀芯示意图如图2所示,和均为导向配合面,要求和对于的同轴度为0.01mm。在历史批次阀芯加工过程中,和对于的同轴度极易超差,从而影响双密封配合面密封。所以,保证和对于的同轴度是保证双密封合格的关键要素。
在细长轴磨削过程中,工件极易产生形状变形,严重影响工件加工质量。形状误差产生机理是复杂的,随着磨削的进行,砂轮在逐渐磨损,将导致磨削深度的逐渐减小,进而使工件形状有产生锥形的趋势。同时,磨削力的作用下,工件会发生弹性变形。双密封阀芯属于细长轴的一种,其形位公差超差主要来自于两个方面:(1)砂轮磨削过程中挤压阀芯,导致阀芯产生变形;(2)阀芯装夹误差导致的形位公差超差。阀芯磨削过程中的形位公差控制问题是一个亟待解决的问题。
3.1 细长轴双密封阀芯导向面理论模型
3.1.1 细长轴双密封阀芯的精密磨削挤压变形系统模型
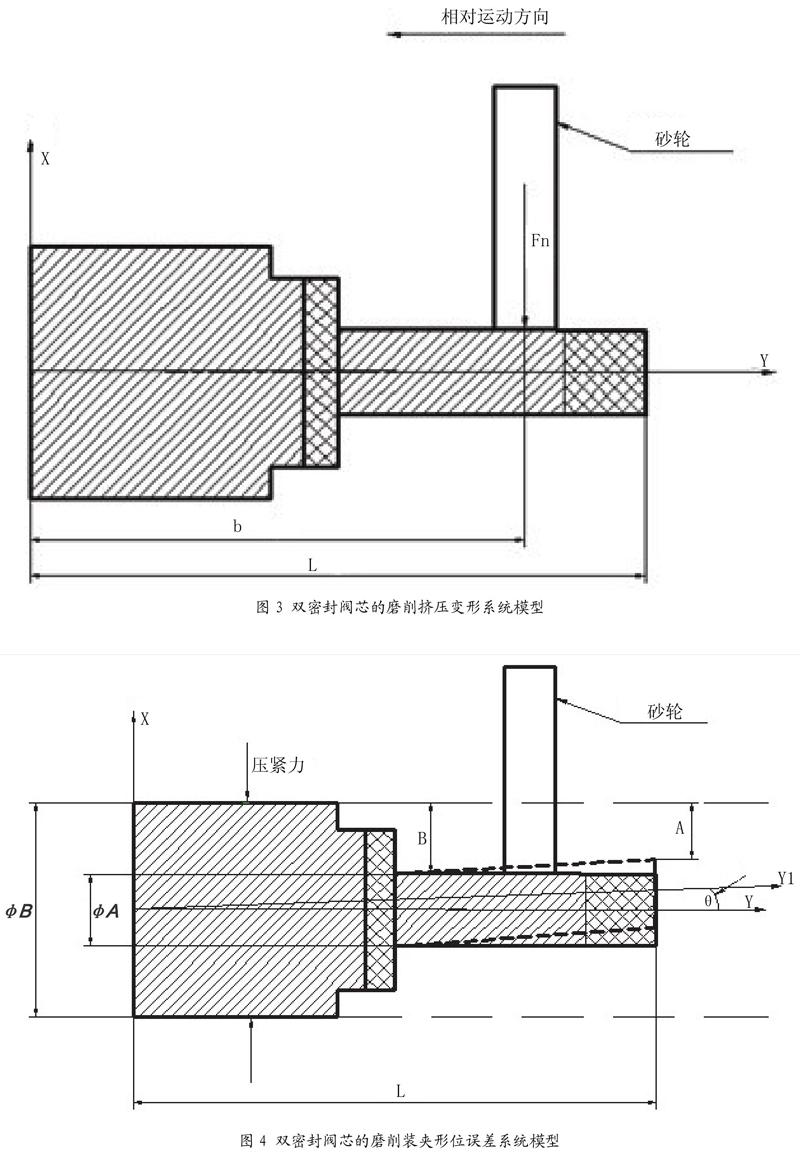
细长轴双密封阀芯的精密磨削挤压变形系统模型,如图3所示。当把阀芯由左端夹罐夹住在磨床上进行磨削时,磨床、阀芯、砂轮构成了一个弹性系统。当砂轮与工件表面接触时,X向的磨削力Fn使阀芯在接触面的X轴负方向上产生弹性变形,致使加工后的工件产生形位误差。由于砂轮在X轴负方向产生的力比阀芯悬臂的重力和Y轴方向的力大的多,故忽略不计。
其中,Fn为磨削过程挤压产生的X轴负方向的集中载荷,L为阀芯总长度,b为阀芯磨削过程中任意一点的位置尺寸。所以,Fn在阀芯Y轴方向任意位置X处的曲率方程为:
式中,E为阀芯的弹性模量,I工件的转动惯量,δ为阀芯的变形量。将式(1)积分二次得:
式中,C和D为积分常数。
由公式(3)可知,在阀芯磨削过程中,磨削挤压力Fn越小,阀芯变形量小。而外圆磨削力[3]为:
其中,r为工件半径,为常数,γ为磨粒圆锥半顶角,为磨削深度,w为有效磨粒间隔,vs为砂轮圆周速度,R为砂轮半径,e=0.2~0.5,vf为纵向进给速度,vw为工件速度。则:
3.1.2 细长轴阀芯装夹形位误差系统模型
双密封阀芯的同轴度、垂直度为阀芯的重要参数,设计要求必须保证在0.015mm以内。阀芯磨削装夹后,悬臂部分的长度相对较长,而关键的塑料密封面则位于阀芯装夹的最远处,装夹时若夹罐出现偏差或跳动,则在阀芯塑料密封面处的偏差会形成一定比例的放大,导致形位公差超出设计要求值。根据该阀芯的历史研制经验,阀芯装夹外圆找正在0.01mm范围内时,阀芯塑料端的形位公差较大甚至超差;将阀芯装夹精度找正在0.005mm范围内时,会对机床精度、装夹精度、砂轮精度和操作人员水平提出更高的要求,同时并不能保证阀芯塑料端的形位公差满足设计要求。
现加工方案为夹罐装夹,砂轮对外圆进行磨削,然后装夹外圆,对外圆进行磨削,两次装夹均存在装夹误差。阀芯装夹形位误差系统模型如图4所示,阀芯总长为L,当阀芯装夹后行程偏差角度时,阀芯相对于基准外圆的偏差为(B-A)。
3.2 基于参考坐标系的阀芯精密磨削参数控制研究及实验验证
基于参考坐标系的阀芯精密磨削方法研究:
经分析可知,阀芯装夹形成的形位误差主要来源于基准的不一致,关键在于重新构建磨削过程的参考坐标基准。考虑到磨床本身的精度较高,通过磨削过程建立参考基准,则精度可达到微米级。
本文提出基于参考坐标系的阀芯磨削方法,通过磨削过程首先建立两次重复装夹的参考基准坐标,然后以建立的参考基准为后续磨削的基准,解决阀芯装夹导致的形位误差问题。
基于参考坐标系的阀芯磨削方法如图5所示,包含以下步骤:
(1)建立参考坐标基准:装夹外圆,对阀芯A位置、B位置同时走刀进行磨削,使阀芯在砂轮A位置形成了新的坐标系(XA,YA),在砂轮B位置形成了新的坐标系(XB,YB),由于砂轮A位置和砂轮B位置是同一次加工而成,则OA、和OB位于同一轴线上且磨床的重复定位精度0.002mm。
(2)磨削外圆:在参考坐标基准建立的基础上,对外圆进行磨削,则构建砂轮A位置、砂轮B位置和外圆剩余部分三处形成的轴线。由于外圆剩余部分和砂轮B位置在同-轴线上,参考步骤(1)中的结论,则外圆剩余部分形成的轴线位于砂轮A位置、砂轮B位置形成轴线的延长线上。
(3)磨削外圆:重新装夹外圆,由于外圆经过上述步骤后精度非常高,则找正砂轮A的位置,对外圆进行磨削,即可保证外圆外圆剩余部分形成的轴线与已经形成的轴线共轴。
在基于参考坐标系阀芯磨削方法应用在基础上,研究纵向进给速度vf、切削深度、工件转速vw对阀芯变形的影响关系,建立三因素正交试验[4]。砂轮的纵向进给速度选择0.5mm/min、0.3mm/min、0.1mm/min;切削深度选择0.1mm、0.05mm、0.03mm;工件转速选择500r/min、300r/min、100r/min。对磨削后的阀芯进行计量得到实验数据如表1所示。通过极差的计算可知,纵向进给速度对阀芯形位公差的影响最大,其次是工件转速,切削深度对阀芯磨削后形位公差影响较小。
通过分析基于参考坐标的阀芯磨削正交试验数据可知,第9组试验的阀芯塑料端同轴度计量实测值最优。由于纵向进给速度对阀芯磨削的影响最大,其参数尽可能降低。所以,选择第9组试验的磨削参数作为最终的磨削参数指标。
以砂轮的纵向进给速度选择0.1 mm/min、 切削深度选择0.03mm、工件转速选择300r/min为阀芯磨削参数,并将基于参考坐标的阀芯磨削方法进行应用,对10件阀芯进行磨削,对10件阀芯的塑料端同轴度进行计量。如图6所示,阀芯塑料端同轴度最大值为0.01mm,最小值为0.006mm,满足设计要求。
3.3 产品应用情况
为了保证双密封形位公差满足设计要求,通过基于参考坐标系的阀芯磨削参数优化和实验验证,双密封阀芯磨削时采用基于参考坐标系的磨削方法,并将磨削参数设置为纵向进给速度选择0.1mm/min、切削深度选择0.03mm、工件转速选择300r/min。经过某型号02批閥芯的应用情况如表2所示,投产阀芯共480件,阀芯塑料端同轴度经计量后仅超差9件,极大地提高了阀芯形位公差的合格率。
4 产品应用
通过基于参考坐标的细长轴双密封阀芯精密磨削参数控制方法,某型号批次阀芯的形位公差合格率提高到97%,远远超出了产品研制时的水平。本文建立了阀芯精密磨削过程中的挤压变形系统模型和装夹形位误差系统模型,提出了基于参考坐标的阀芯磨削参数控制方法并通过实验和产品进行验证,效果显著提高。本文研究方案通过在某批次产品生产制造过程中进行应用,取得了良好的效果,具有一定的理论意义和工程应用价值。
参考文献:
[1] 刘丰林,康权,宋晓.螺旋面成形磨削误差补偿砂轮截形研究[J].机械科学与技术,2014,33(05):662-666.
[2] 康念辉,李圣怡,郑子文.基于多体系s统理论的非球面磨削误差模型与补偿技术[J].机械工程学报,2008(04):143-149.
[3] 丁宁.外圆纵向智能磨削研究[D].吉林大学,2004.
[4] 张振中.陶瓷模具材料微细柱面阵列的高效精密磨削技术研究[D].山东大学,2020.
