新型上承式拱桥动力特性研究与试验验证

2021-11-13颜晨宇庞木林谢肖礼

铁道科学与工程学报 2021年10期

颜晨宇，庞木林，谢肖礼

(广西大学土木建筑工程学院，广西南宁 530004)

上承式拱桥刚度大、跨越能力强，且经济性、耐久性良好，能够很好地满足西部山区桥梁建设的需求，因此，在活载比重大、动力问题比较突出的铁路桥梁中，上承式拱桥一直是大跨径桥梁选型中具有很强竞争力的结构形式[1−3]，如大瑞铁路主跨达490 m的怒江大桥[4]、主桥长445 m的沪昆客专北盘江大桥[5]，以及蒙华铁路洛河大桥[6]和板布河大桥[7]等。高速铁路上列车行驶速度高，对桥梁的力学性能要求严格，为满足高速行车需求[8−9]，在拱桥设计时，结构体系的选择和刚度、动力特性等问题不可忽视。目前上承式拱桥不断往超大跨径方面发展，结构面临自重过大、刚度减小[10]、自振频率降低等问题，极大地影响了列车在运行中的平稳性和舒适性[11]。而且，如果上承式拱桥的自振频率过小，将极易引发共振导致发生结构性破坏，造成难以挽回的损失。可见，动力特性对高速铁路拱桥自身和行车安全有着关键性的影响。目前，不同学者对于拱桥动力特性的研究各有侧重。遆子龙等[12]基于有限元和流体动力学计算方法，研究了典型细长杆件在全桥约束下的自振频率及涡振发生风速，研究表明结构内力及节点板长度会改变局部杆件的自振频率。郑晓龙等[13]利用MSC软件建立南盘江大桥车桥耦合动力模型，研究了列车经过时拱桥的动力响应规律，为解决同类型桥梁的车桥动力研究提供了参考。NGUYEN等[14]建立了的风−车−桥全耦合相互作用模型，研究了某细长拱桥在狂风及车辆作用下的动力特性，探讨了狂风环境下细长拱桥行车的安全性及舒适性。张强[15]利用ANSYS软件对千岛湖大桥的自振特性进行参数分析，为大跨度上承式钢管混凝土拱桥的冲击系数的取值提供一定的依据。曾勇等[16]利用ANSYS软件对某上承式钢管混凝土拱桥进行了动力特性研究和横向静风响应分析，为研究上承式钢管混凝土拱桥的面内及面外振型提供参考。ATAEI等[17]通过动荷载试验研究了圬工拱桥的动力放大系数，探讨了不同因素对动力放大系数的影响。由上述文献可以看出，国内外学者对于上承式拱桥动力特性的研究主要停留在现有的拱桥结构形式上，以结构创新为途径进而改善其动力特性方面的研究较少，但是结构体系创新能从根本上改变结构的力学性能，对提高上承式拱桥动力特性有着十分重要的作用。为从创新拱桥结构上着手改善其动力特性，本文提出一种兼具拱结构和桁架结构优点的新型上承式拱桥，即把立柱改为三角网，并将三角网中的部分杆件连成拱形构成副拱，形成双层桁架结构，通过提高结构的刚度，进而使结构的动力特性得到改善。以下阐述新型上承式拱桥的力学原理，修建试验桥进行环境激振试验验证理论分析和有限元计算结果，利用有限元软件研究其动力特性和刚度，并进行拱肋强度及结构的稳定性分析。

1 新型上承式拱桥动力特性研究

动力特性是结构固有的特性，主要包括其自振频率、振型和阻尼比，与结构组成体系、边界条件、材料类型等有关[18−19]。由公式可知，结构的自振频率与刚度的平方根成正比，因此，提高上承式拱桥整体刚度可直接增大其自振频率。

根据以上分析，本文所提出的新型上承式拱桥主要通过提高结构刚度进而增大其自振频率，其具体思路是，用三角网取代立柱，并将三角网中的部分杆件连成拱形构成副拱，形成双层桁架结构，从而使结构的刚度得到提高，进而改善结构的动力特性。新型上承式拱桥(下文简称“本文拱桥”)，主要由主拱、副拱、主梁和三角网组成，结构形式如图1，以下阐述其力学原理。

图1 新型上承式拱桥结构形式Fig.1 Structure of new type deck arch bridge

1.1 引入三角形稳定理念，提高结构刚度

对于传统上承式拱桥，拱上立柱仅对主梁起到多点弹性约束的作用，提高了其线刚度，而对拱肋的刚度没有贡献。将立柱改为三角网后，三角网与主梁及拱肋形成了系列连续的三角形，因三角形具有良好的稳定性，主梁及拱肋的线刚度均得到有效提高，从而提高了结构的局部刚度及整体刚度。

随着上承式拱桥跨径的增大，主梁与拱肋之间的杆件自由长度增大，超过一定长度后，其轴向线刚度i=(EA)/l变小，杆件受非节点力的特征将十分明显，大大降低了三角网的线刚度及稳定性。

解决问题的优选方案是减小构件的长度：如图2(a)所示，将三角网中的部分杆件连成拱形，形成副拱(MN)，其拱脚与新增的斜腿相接，使力直接传给基础。副拱既能减少三角网杆件自由长度，又分别与主拱、主梁形成桁架结构，从而形成双桁双拱结构，如图2(b)所示。

图2 双桁双拱结构示意图Fig.2 Structure of double truss double arch bridge

1.2 增加副拱，为主拱卸载

为了减小原主拱中间区域所承受的荷载，将三角网中的部分杆件连成拱形构成副拱，并将其拱脚与基础相连，桥面荷载往下传递时，部分荷载经上层三角网传到副拱后可直接传至基础，因此可为主拱卸载，主拱卸载示意图如图3。

图3 双拱荷载分担原理Fig.3 Load sharing principle of double arch

2 本文拱桥试验研究

为验证本文拱桥动力特性的优越性，修建一座新型上承式拱桥试验桥和一座传统上承式拱桥试验桥，对其进行脉动试验，测出两者首次发生面内竖弯的自振频率，并与有限元模型计算结果进行对比分析。

2.1 试验桥结构参数

2座试验桥跨径均为10 m，桥面全宽1.08 m，拱轴线为悬链线，拱轴系数取m=2.8，矢跨比为1/5，试验桥结构布置如图4～5，主要构件参数见表1。对比拱桥主梁与立柱和墩台之间设矩形板式橡胶支座，本文拱桥三角网杆件之间，以及三角网杆件与主梁和拱肋之间采用焊接连接。

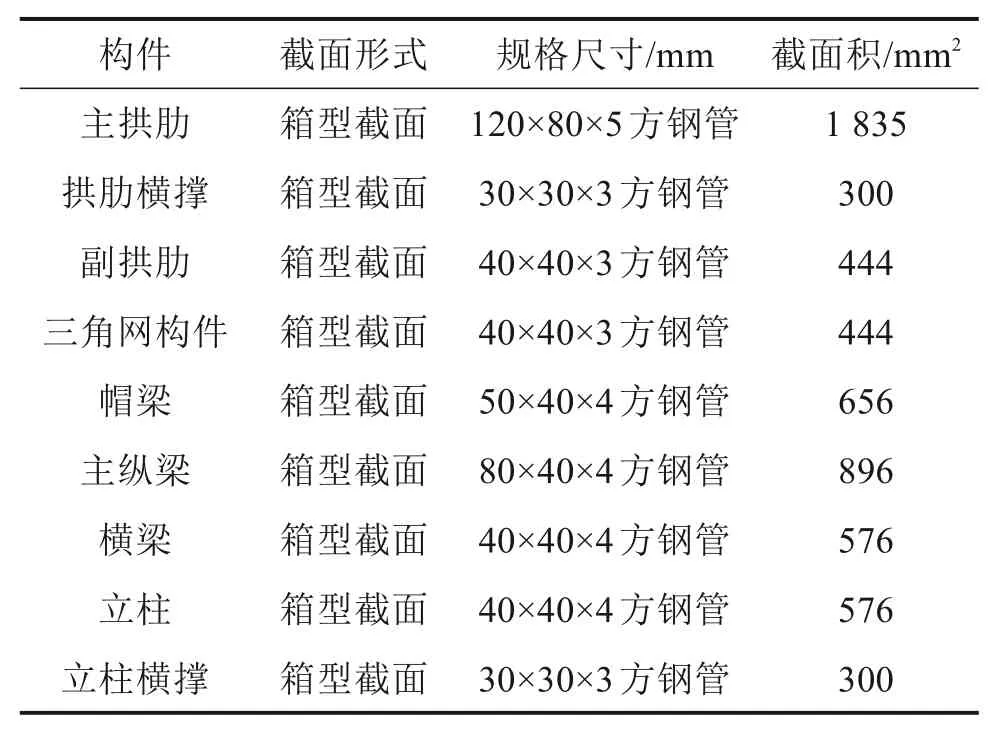
表1 试验桥主要构件参数Table 1 Parameters table of members of the test bridge

图4 本文拱桥试验桥立面图Fig.4 Elevation drawing of the test bridge of the arch bridge in this paper

2.2 试验桥有限元分析结果

通过有限元软件分别建立2座试验桥的模型，分析结构的自振频率和振型。有限元分析结果见表2。

表2 试验桥有限元模型自振频率及振型Table 2 Natural frequencies and vibration modes of the finite element model of the test bridge

图5 对比拱桥试验桥立面图Fig.5 Elevation of the test bridge of the arch bridge of contrast

有限元分析结果表明，在同一阶模态下，本文拱桥的自振频率与传统上承式拱桥相比有很大提高，且振型出现的次序也有着较大区别，前者发生面内振动的阶次较高、阶数较少。传统上承式拱桥首次发生面内振动时的自振频率仅为11.80 Hz，而本文拱桥的自振频率高达36.65 Hz，提高了210.6%；首次发生扭转振动时，传统上承式拱桥自振频率为21.45 Hz，本文拱桥自振频率为30.98 Hz，提高了44.4%；首次发生面外振动时，传统上承式拱桥和本文拱桥的自振频率分别为14.26 Hz，14.68 Hz，后者比前者略有提高。

可见，采用三角网取代平行立柱后，本文拱桥的面内、面外和扭转刚度均比传统上承式拱桥有着不同程度的提高，其中尤以面内刚度提高的效果最为明显。

2.3 环境激振试验结果分析

本次环境激振试验基于有线模态测试系统进行测试，试验中所采用的拾振器为2D001V磁电式速度传感器，总共设置3个测点，分别设在主梁1/4处、1/2处和3/4处，现场试验如图6。动态信号采集则选用DH5981动态信号采集仪，测试过程中本文拱桥的采样频率为200 Hz，传统上承式拱桥的采样频率为50 Hz，每次试验采样时间为30 min。采集完成后，通过DHDAS动态信号采集分析系统对试验桥振动加速度时程曲线进行频谱分析，得到3处测点所对应的频谱曲线，如图7～8。表3为2座试验桥首次发生面内振动时自振频率的有限元值和试验值，图9为试验桥首次发生面内竖弯时的试验振型。

图7 对比拱桥频谱图Fig.7 Spectrum of the arch bridge of contrast

图9 振型Fig.9 Vibration mode

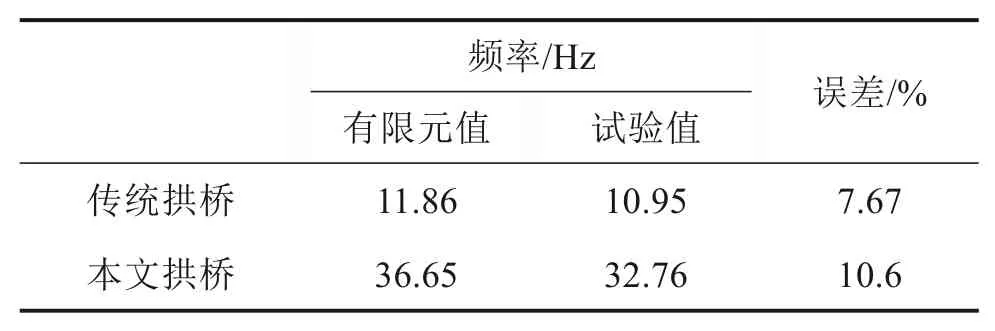
表3 试验桥首次发生面内竖弯自振频率对比Table 3 Comparison of natural frequency of vertical bending in the plane for the first time

图6 现场试验图Fig.6 Field test drawing

由试验结果可以看出，首次发生面内竖弯振动时，本文拱桥和传统上承式拱桥的自振频率试验值分别为32.76 Hz和10.95 Hz，前者比后者提高199.1%，与有限元分析结果相比，试验值的误差分别为10.6%和7.67%，且试验所测得的模态振型与有限元所得模态振型一致。综合考虑有限元分析时对试验桥边界条件的理想化处理，以及施工时可能存在的一些不可避免的缺陷，试验结果的可靠性和准确性较高，可为本文拱桥动力特性的研究提供佐证。

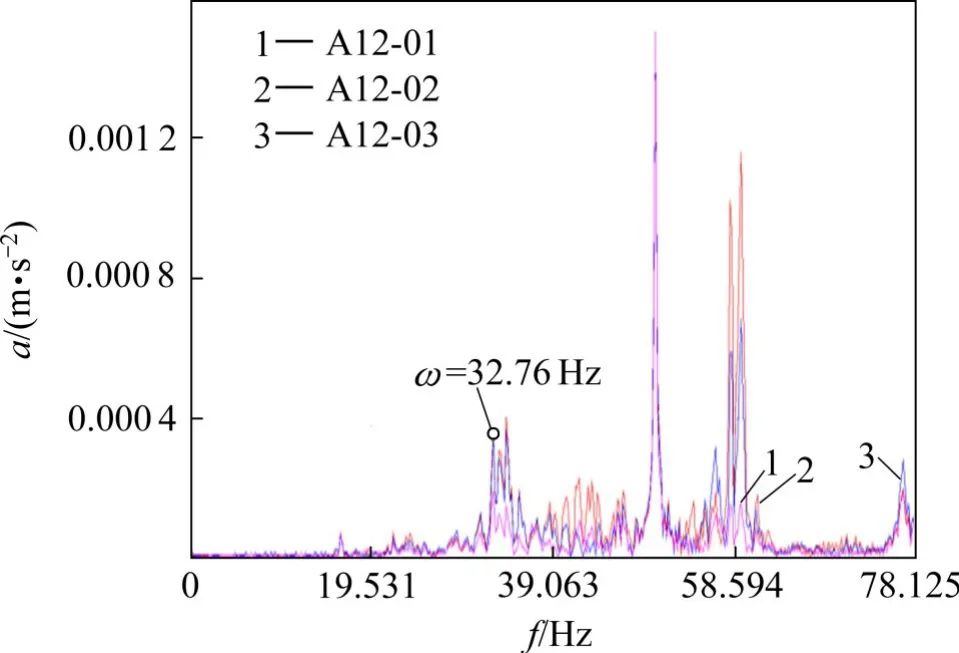
图8 本文拱桥频谱图Fig.8 Spectrum of the arch bridge in this paper

3 本文拱桥有限元分析

为进一步验证本文拱桥动力特性的优越性，采用有限元软件建立本文拱桥的模型，计算其动力特性和刚度，并将计算结果与传统上承式拱桥进行对比，此外，研究了三角网杆件刚度对结构动力特性的影响。

3.1 结构参数设置

以500 m双线铁路拱桥为例，拱轴线为悬链线，拱轴系数m=2.7，矢跨比1/5，桥面宽度为25 m。通过控制拱圈、三角网杆件和立柱的构件参数，保证本文拱桥和对比拱桥的用钢量相当(约为2.17万t)。表4～5给出了两者主要构件参数及材料用量，图10为本文拱桥结构布置图，图11为本文及对比拱桥拱肋结构布置图。

表4 对比拱桥主要构件参数及材料用量Table 4 Parameters and amount of main members of the arch bridge of contrast

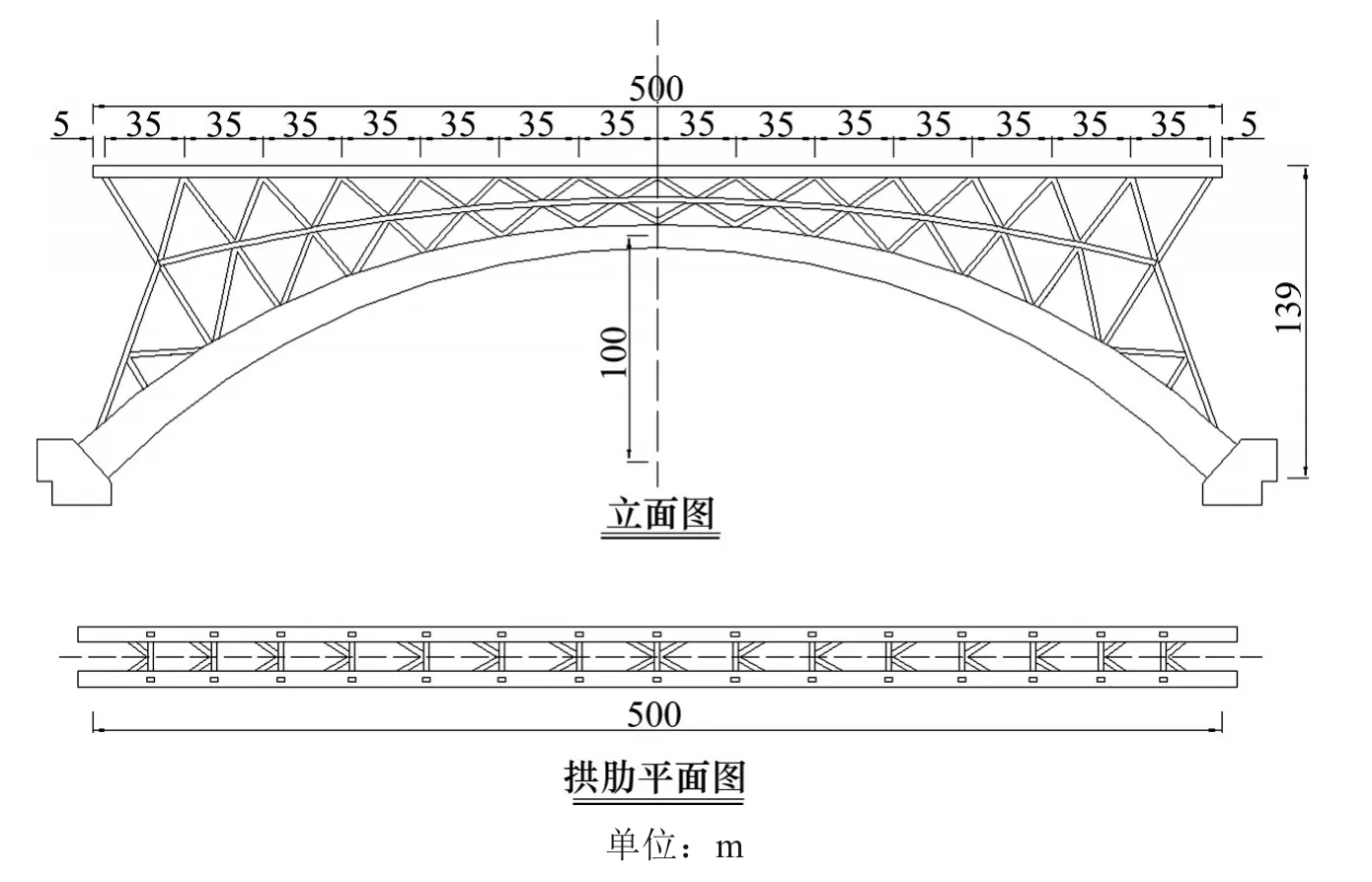
图10 结构布置图Fig.10 Layout drawing

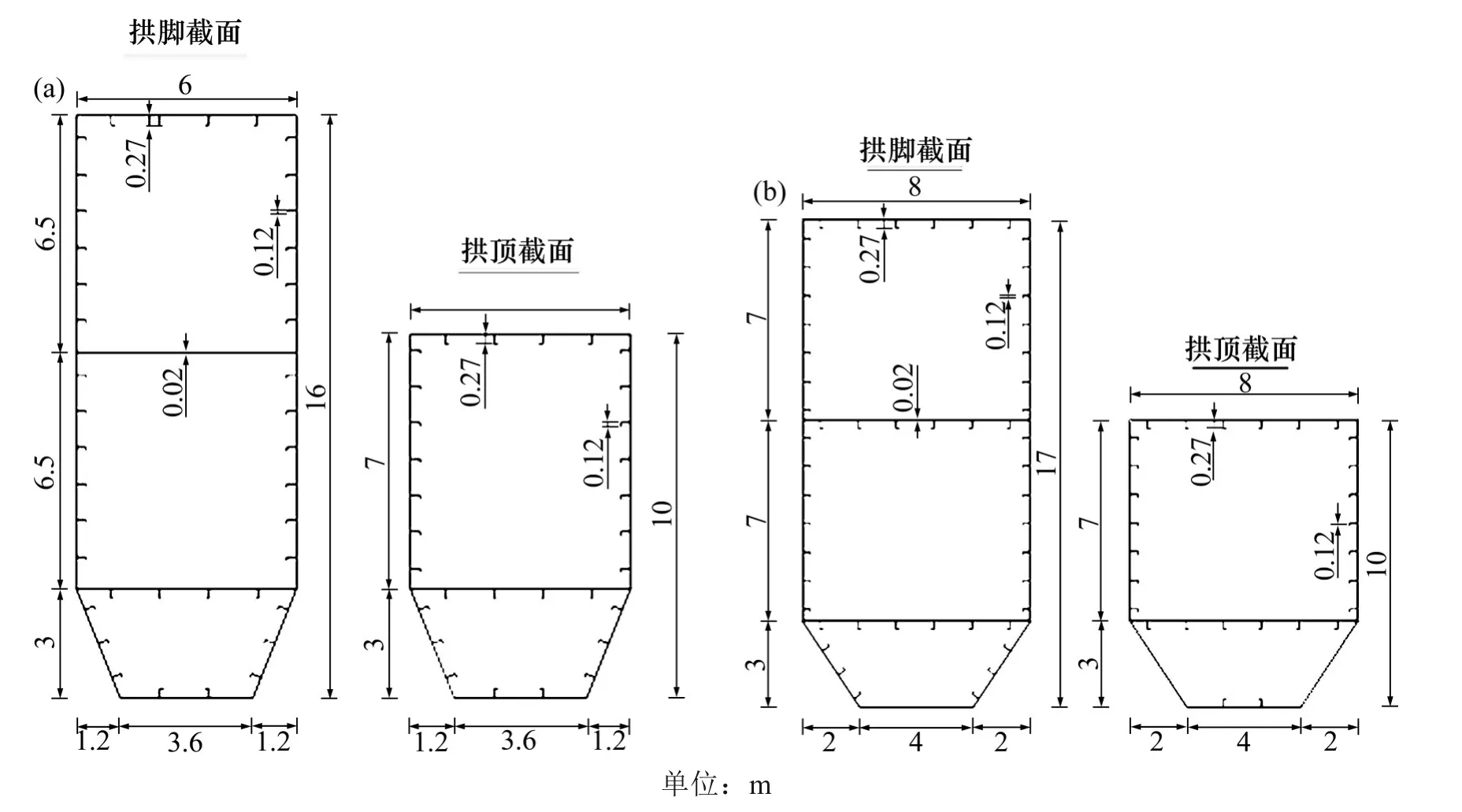
图11 拱肋截面Fig.11 Cross section of arch

表5 本文拱桥主要构件参数及材料用量Table 5 Parameters and amount of main members of the arch bridge in this paper

3.2 结构动力特性分析结果

由表6的有限元分析结果可知，本文拱桥首次出现面外侧弯、面内竖弯和扭转的自振频率分别为0.227，0.803和1.321 Hz，而传统上承式拱桥则为0.197，0.436和0.535 Hz，前者分别比后者提升了15.2%，84.1%和146.9%；而从振型出现次序来看，传统上承式拱桥前3阶振型分别为面外侧弯、面内竖弯和扭转振动，而本文拱桥首次出现面内和扭转振动的阶次有所延后，可见，三角网取代立柱后，结构的面内和扭转刚度有明显提高。

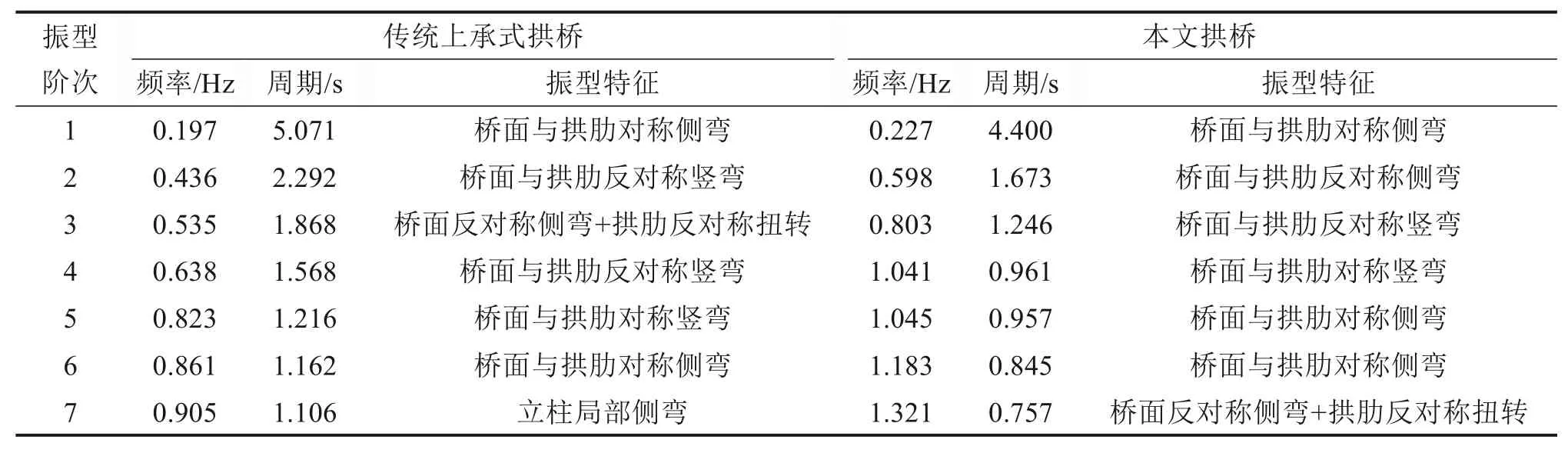
表6 有限元自振频率及振型Table 6 Natural frequencies and vibration modes of the finite element model

综上可知，尽管在保证用钢量相当的前提下，本文拱桥的自振频率与传统上承式拱桥相比仍有较大幅度的提高，因此，本文拱桥不仅在动力特性方面有着明显的优越性，其经济指标也较为良好，在方案比选时有着一定优势。

3.3 结构刚度分析结果

本文拱桥通过提高结构的刚度来达到提高其自振频率的目的，为对该理论的正确性进行验证，在3.1节所建拱桥模型的基础上，依据《铁路桥涵设计规范》[20]要求，考虑3个荷载工况：①列车活载+0.5倍温度荷载；②0.63倍列车活载+温度荷载；③列车活载，对结构的刚度进行计算。其中，列车荷载采用ZK活载，初始温度为15℃，升温最终温度为40℃，降温最终温度为−2℃。表7给出了结构在不同荷载工况下的主梁挠度计算结果。

表7 主梁挠度对比Table 7 Comparison of deflection of main beam

有限元计算结果表明，在荷载工况①作用下，对比拱桥主梁最大挠度为164.79 mm，而本文拱桥最大挠度仅为119.01 mm，比前者减少27.8%；在荷载工况②作用下，对比拱桥和本文拱桥主梁最大挠度分别为199.79 mm和159.41 mm，后者比前者减少20.2%；在荷载工况③作用下，两者主梁最大挠度分别为98.99 mm和57.51 mm，后者比前者减少41.9%。

综上可知，将立柱改为三角网后，本文拱桥在不同荷载工况下的主梁最大挠度均小于传统上承式拱桥，可见，结构的刚度得到大幅提高后，其动力特性亦随之改善。

3.4 拱肋强度分析

利用三角网杆件替换立柱后，三角网与主梁及拱肋形成了系列连续的三角形从而提高了结构的局部刚度及整体刚度，并达到为拱肋卸载的目的。为验证三角网杆件的加入对拱肋卸载作用，现对2座拱桥在列车活载下的拱肋应力分布进行分析。

图12～13为本文拱桥及对比拱桥在列车活载下的拱肋应力图。由图可知，在列车活载作用下对比拱桥及本文拱桥拱肋最大压应力分别为44.15 MPa和27.47 MPa，后者比前者减少37.8%。此外，本文拱桥在跨中处的压应力仅为9.01 MPa，远小于对比拱桥。

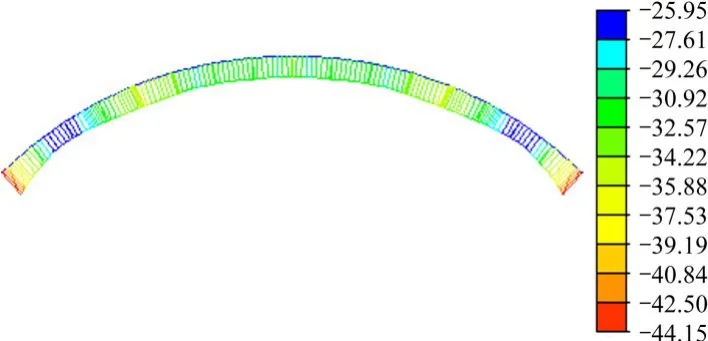
图12 对比拱桥拱肋压应力云图Fig.12 Compressive stress nephogram of arch ribs of the arch bridge of contrast

图13 本文拱桥拱肋压应力云图Fig.13 Compressive stress nephogram of arch ribs of the arch bridge in this paper

可见，采用三角网杆件的引入使得拱桥形成了变高桁架体系，结构整体受力，分担了荷载作用下拱肋应力，从而大幅提高了拱桥结构整体刚度，进而使得拱桥动力特性得到改善。

3.5 三角网杆件及全桥稳定性分析

考虑恒载及活载同时作用，分别对结构进行一类稳定稳定性分析。通过有限元计算，结构首次失稳现象发生在三角网杆件横联处，稳定安全系数为5.656。此外，结构前3阶杆件局部失稳时的稳定安全系数分别为5.656，5.882和8.296。同时，表8给出了本文拱桥前3阶发生整体失稳时的失稳模态和稳定安全系数。由表8可知，结构首次发生整体失稳时的稳定安全系数为15.64，失稳模态为面外正对称。