正态信息扩散法推断岩土参数概率分布的窗宽优化和区间截尾问题研究

孔令奇，李翠娟

(1.成都工业学院 材料与环境工程学院，四川 成都 610031；2.西南交通大学 土木工程学院，四川 成都 610031)

岩土参数概率分布的研究一直是一项基础性研究工作，具有极其重要的价值和意义[1−3]。国内外研究人员已做了大量工作[4−7]，提出了多种岩土参数概率分布拟合方法，主要包括参数估计[8−9]和非参数估计2种[10−12]。基于非参数估计的主要有最大熵法、正交多项式等方法[1−3,10−12]。宫凤强等[13]系统考察了经典分布拟合、最大熵法、一般多项式法、正交多项式法和正态信息扩散法在推断岩土参数概率分布的优劣，最终确定正态信息扩散法为相对最优的推断方法。宫凤强等[10]提出正态信息扩散法推断小样本岩土力学参数概率密度函数的有效性。朱唤珍等[1]进一步证明正态信息扩散法在大样本岩土参数概率分布推断中的有效性，但该方法在应用的过程中存在窗宽选择困难和截尾误差的问题[14]。朱唤珍等[1]给出了最优窗宽的计算方法，但忽略了窗宽选择与频率直方图的匹配关系，且对于岩土参数测试样本来说，由于受经济技术条件限制，岩土体参数的试验数据比较有限[15]，难于满足最优窗宽的取值条件。宫凤强等[16]给出了正态信息扩散法截尾分布的处理方法，正态信息扩散法采用Gaussian作为核函数时，正态分布属于无界分布，拟合曲线的首端和尾端向两边延展，给出的c3取值方法是针对样本区间的截尾方法，但其扩大了正态信息扩散分布的拟合边界。本文在既有研究基础上提出正态信息扩散法窗宽确定方法，在不同直方图分组基础上，获得测试样本“匹配窗宽”；基于正态信息扩散分布首尾延展特性，结合岩土参数实测数据的分布特征，提出“收窄”正态信息扩散分布取值区间的方法；通过工程实际测试样本验证本文方法的有效性和合理性，完善正态信息扩散法在岩土参数概率密度函数拟合上的应用。

1 正态信息扩散法窗宽确定

1.1 正态信息扩散法的概率密度函数

为了避免区间划分对概率密度函数曲线形状的影响，正态信息扩散法考虑以任意一点x为中心的邻域，统计落入这个区间的样本点个数，区域的位置随着x的变动而变动，任意一点x处的概率密度函数值由区域内的样本点数决定。

设X1,X2,…,Xn是取自总体X的样本，则样本的概率密度函数为[1,17-19]

其中，K()为核函数；h为窗宽，即每个区间的长度；n为样本个数。

1.2 既有窗宽确定方法

窗宽是正态信息扩散法推断概率密度函数中一个重要的指标。文献[1]和[17]提出通过求解积分均方误差MISE(mean integrated squared error)函数的最小值获得最优窗宽，即

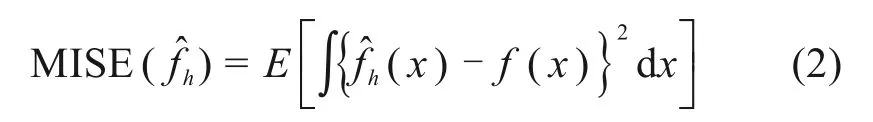
其中：f(x)为样本总体的实际概率密度。

当K(x)满足如下条件时：

1)K(x)在区间[−1,1]取值，且要求对称；

2)∫K(x)dx=1；

3)∫xK(x)dx=0；

4)∫x2K(x)dx=σ2k>0，σk为标准差。

则

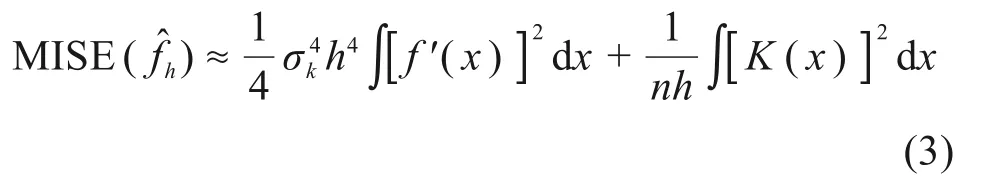
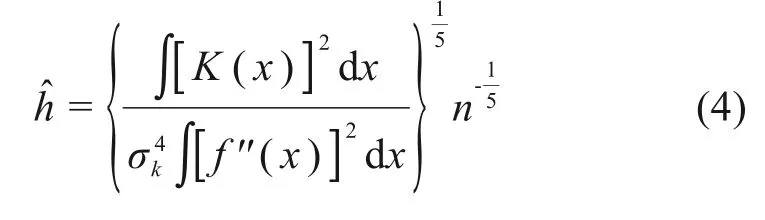
但获得式(4)还有一个最关键的前提条件，即满足h→0，nh→+∞时[17]，式(4)才近似相等。对于岩土参数测试样本来说，由于受经济技术条件限制，岩土体参数的试验数据比较有限[15]，难于满足此条件。所以对岩土参数测试样本来说，采用正态信息扩散法拟合其概率密度函数时，通过式(4)计算出的h值并非最佳窗宽。

在此仅以文献[20]提供的内摩擦角φ的测试样本为例(样本81组，具体样本值见文献[20])，详细说明窗宽取值对拟合精度的影响，更多测试样本的分析结果见1.3.2节。当直方图分组数取为10时，采用不同窗宽拟合内摩擦角φ测试样本的概率密度函数，拟合曲线如图1所示。

图1 内摩擦角样本不同窗宽下的拟合曲线Fig.1 Fitting curves of cohesion samples under different window widths

K-S检验法的检验量是整个取值范围内的最大偏差值，在一定的显著性水平下，可评估某一分布拟合的有效性，但不能提供某一分布拟合是良好的绝对信息[21]。均方差可从全局角度评估正态信息扩散法对岩土参数概率密度函数的拟合质量，故本文采用均方差(Mean Squared Error，MSE)指标检验拟合曲线的优劣[22]

式中：fi为理论频率；S*(xi)为频率直方图中每个子区间的相对频率；m为区间个数。

内摩擦角样本在不同窗宽下采用正态信息扩散法推断其概率密度函数时的均方差指标统计值如表1所示。

表1 内摩擦角样本的检验结果Table 1 Test results of internal friction angle samples

由图1和表1明显可见，当采用式(4)计算的窗宽拟合内摩擦角样本的概率密度函数时，拟合误差最大，均方差指标为0.084 3，随着窗宽取值的减小，拟合误差在h/3时达到最小，均方差指标为0.035 7，继续减小窗宽，拟合误差增大。所以，对于内摩擦角测试样本，其最佳的匹配窗宽是h/3，h并非最佳窗宽。

1.3 匹配窗宽确定

1.3.1 直方图分组

理论和实测数据均已显示选择窗宽h做为正态信息扩散法的最优窗宽是不恰当的，对既有研究工作总结发现，目前对岩土参数概率密度函数曲线的拟合不论是基于参数估计还是非参数估计法，均是根据测试样本获得直方图，而直方图绘制依赖于区间的划分，区间划分的不同直接影响曲线的形状和拟合误差的大小。在文献[1]中，作者给出了最佳窗宽的计算公式，但忽略了窗宽选择与直方图的匹配关系，最优窗宽是相对的，所以本文称其为“匹配窗宽”。

仍以内摩擦角的测试样本为例，当直方图分组数取为5和20时，其正态信息扩散分布的拟合曲线如图2～3所示。直方图分组为5时检验结果统计值如表2所示。直方图分组为20时检验结果统计值如表3所示。

表2 分组为5时检验结果Table 2 Test result when grouping is 5

表3 分组为20时检验结果Table 3 Test result when grouping is 20

图2 分组为5时拟合曲线对比Fig.2 Comparison of fitting curves when grouping is 5

图3 分组为20时拟合曲线对比Fig.3 Comparison of fitting curves when grouping is 20

由图1～3明显可见，当直方图分组数取为5时，最佳匹配窗宽为h/2；当直方图分组数取为10时，最佳匹配窗宽为h/3；当直方图分组数取为20时，最佳匹配窗宽为h/5。测试样本直方图分组数越大，应采用较小的匹配窗宽；直方图分组数越小，应采用较大的匹配窗宽。所以，采用正态信息扩散法推断岩土参数概率分布的前提是确定测试样本直方图的分组数。

文献[23]指出，确定直方图分组数的原则是分组的结果能正确反映数据的分布规律，组数应根据数据多少来确定。组数过少，会掩盖数据的分布规律；组数过多，使数据过于零星分散，也无法显示样本分布状况。

在概率论与数理统计中，对于正态分布总体的随机变量，其直方图子区间的划分与样本数量有最佳关系，取分组数m=1.87(n-1)2/5[21]。但大量的研究工作已表明，岩土参数测试样本离散性严重，呈偏态分布。所以，对于工程中非正态分布的随机变量总体，文献[24]指出，当样本个数大于50时，可将直方图绘制时的分组数m取为

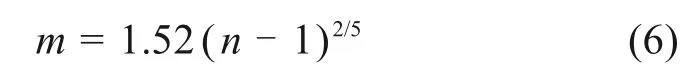
其中，n为样本个数。

对于岩土参数测试样本来说，由于受经济技术条件限制，岩土体参数的试验数据比较有限[15]，样本个数通常不足50个。文献[23]给出当样本总数在50～100时，直方图分组数取6～10。文献[25]给出当样本数在100以内时，直方图分组数一般分5～12组。

综上所述，本文按如下分组：

当样本个数大于50时，按式(6)进行直方图分组；当样本个数小于50时，直方图分组数取为5或6(依具体样本选择)。

1.3.2 匹配窗宽确定方法

由上文的分析可知，直方图分组数的不同，反映了样本不同程度的波动性和离散性，与之匹配的窗宽值也应是不同的。

根据式(4)计算的窗宽h对波动性较小的岩土参数测试样本适用，但对具有一定波动性的岩土参数测试样本，显然较小的窗宽才合适。

为此，本文提出岩土参数测试样本窗宽选择方法为：取h为初始值，依次改变窗宽的大小为h/2，h/3，h/4…，误差评价指标均方差最小为目标，确定最佳的匹配窗宽h′。

以文献[20]粉质黏土压缩指数(55组样本)、黏聚力c(81组样本)2组大样本和文献[26−28]提供的5组小样本为例，验证本文方法的有效性和准确性。5组小样本岩土参数分别为：内摩擦角正切值(24组样本)[26]、液限(26组样本)[26]、黏聚力(21组样本)[26]、350号混凝土断裂韧度(35组样本)[27]和标准风压(25组样本)参数[28]。拟合曲线如图4～10所示，MSE误差指标如表4所示。

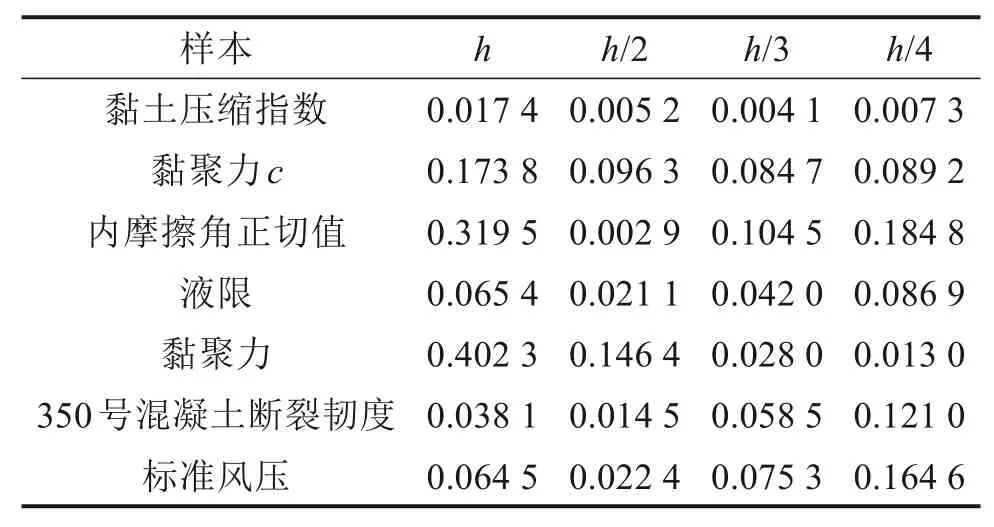
表4 MSE误差评价指标Table 4 MSE error evaluation index

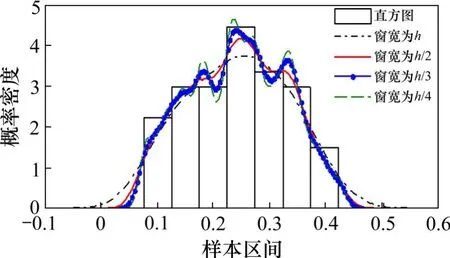
图4 粉质黏土压缩指数样本拟合曲线比较Fig.4 Comparison of fitting curves of silty clay compression index samples

图5 黏聚力c样本拟合曲线比较Fig.5 Comparison of fitting curves of cohesion c samples

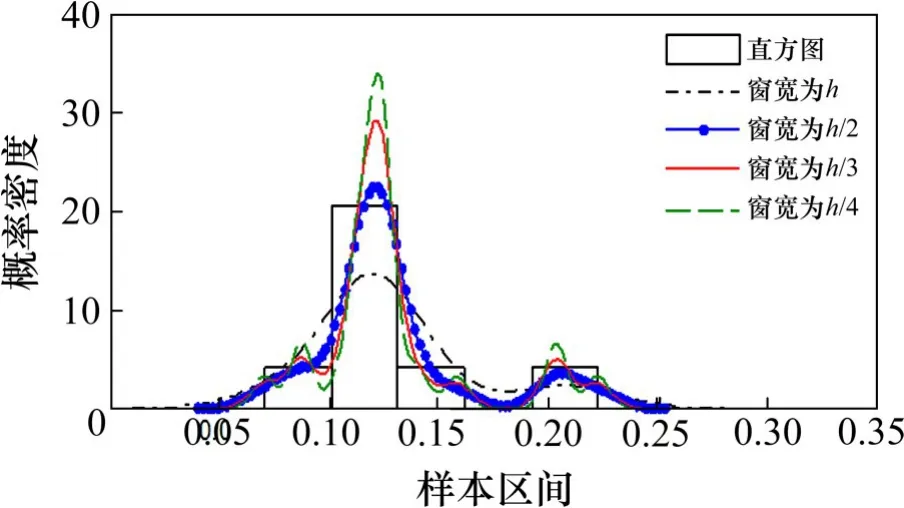
图6 内摩擦角正切值样本拟合曲线比较Fig.6 Comparison of sample fitting curves of tangent value of internal friction angle

图7 液限样本拟合曲线比较Fig.7 Comparison of fitting curves of liquid limit samples

图8 黏聚力样本拟合曲线比较Fig.8 Comparison of fitting curves of cohesive force samples

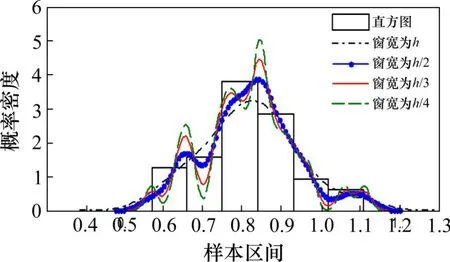
图9 350号混凝土断裂韧度样本拟合曲线比较Fig.9 Comparison of fitting curves of No350 concrete fracture toughness samples

图10 标准风压样本拟合曲线比较Fig.10 Comparison of fitting curves of standard wind pressure samples

由图4～10和表4明显可见：无论是通过拟合曲线的直观对比，还是通过均方差指标的定量检验，都说明本文提出的匹配窗宽下的信息扩散分布所得到的概率密度函数优于h窗宽下的概率密度函数。说明了本文方法在正态信息扩散法窗宽选择中的正确性和适用性。正态信息扩散法推断岩土参数测试样本概率分布的匹配窗宽与测试样本的个数和样本的离散程度相关，每组测试样本的匹配窗宽不同，应单独计算。

正如文献[1]所述，正态信息扩散法能较为理想的推断岩土参数测试样本的概率分布，但存在一个不容忽视的问题，由图1～10也可见，那就是拟合曲线存在上、下截尾误差。

2 拟合边界确定

不论对哪一种岩土参数概率密度函数推断方法，通常尾部样本点分散，取值概率很小，拟合过程中，如果上界选择过大，概率密度拟合曲线的尾部就会出现波动；如果上界选择过小，拟合曲线的尾部会上翘，因为在这种界限附近，样本点尚未明显减少，使得这个点以外的点上的取值概率得以累加。如果样本下界选得过大，拟合曲线在首端的取值概率较大，会使曲线变得平坦。

2.1 既有拟合边界确定方法

文献[16]提出了几种正态信息扩散法区间取值情况：

1)最大、最小值作为区间边界。如图1～10可见，如果选择最大、最小值作为正态信息扩散分布法的拟合边界，显然出现截尾误差，累积概率分布小于1。

2)文中对比分析了3σ，4σ，c33和c3型区间取值方法的优劣，最终确定c3型为最合理的截尾区间。

c3型区间取值方法为：以[μ-3σ,μ+3σ]为基础，参考偏度系数c进行调整，当c<0，左端边界取μ-(3-c)σ，减小下限值；当c>0，右端边界取μ+(3+c)σ，增大上限值。

正态信息扩散分布法推断岩土参数概率分布时首尾延展，超出样本边界，出现截尾误差，继续扩大样本取值边界，会使截尾误差增大。以文献[20]的黏聚力c测试样本(81组)为例，样本最大、最小值为[7,43]，测试样本的偏度系数为0.367大于0，分布右偏，采用c3型截尾区间为[−3.98,49.3]，显然正态信息扩散分布的拟合区间范围超出样本的最大、最小值区间，且下限为负，这与岩土参数的实际分布不符。

2.2 正态信息扩散法拟合边界取值

在一般概率密度拟合方法中，通常取样本随机变量z∈[zmin,zmax]，下界值取稍小于zmin，上界值取稍大于。但该方法不能直接应用于正态信息扩散估计法。比如在确定最大熵法及最佳平方逼近法积分边界时，上、下界限均是在样本最大、最小值基础上增大上界或减小下界，这样取值是将拟合曲线向首尾两端扩展，包络样本边界。但正态信息扩散估计法不同，采用Gaussian作为核函数时，正态分布属于无界分布，拟合曲线的首端和尾端向两边无限延展，远超出样本边界。所以，正态信息扩散估计法中首尾边界的确定方法应与最大熵法等相反，收窄首尾边界，在样本最大、最小值基础上，减小上界、增大下界。

为了确定正态信息扩散法的拟合边界，关键是如何减小上界、增大下界。目前没有经验值、没有统一的标准，更无文献做过系统的研究。

正如文献[16]所述，首尾区间的选择应以实测数据的分布范围为依据，拟合曲线包含样本区间范围，不能取得太宽；确定分布区间取值范围的标准是使该区间内累积概率值接近1。最简单、直接的方法是：确定样本正态信息扩散分布匹配窗宽的基础上，试探减小上界值、增大下界值，直到正态信息扩散分布拟合区间下界值稍大于zmin，上界值稍小于zmax。

为了节约试探取值时间，本文提出借助样本队列曲线法。以文献[20]给出的黏聚力c样本(81组)为例，绘制样本的队列曲线如图11所示。

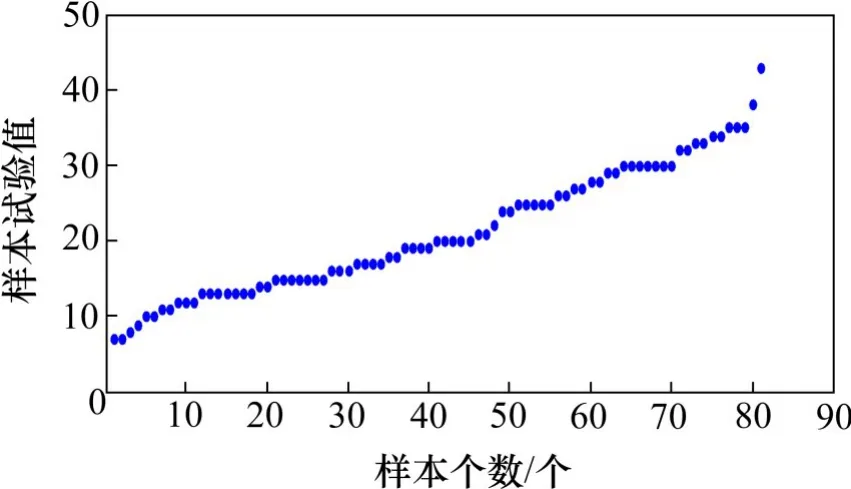
图11 黏聚力c样本队列曲线Fig.11 Cohesion c sample queue curve

由图11可见，黏聚力c首、尾部样本点分散，取值概率很小，正因如此，才造成图12所示的概率密度拟合曲线尾部出现波动，拟合曲线首尾与样本实际概率分布不吻合。为了实现拟合曲线在样本最大、最小值处的概率值为0(或趋于0)，应减小上界，增大下界。根据图11，对于黏聚力c测试样本，样本原取值边界为[7,43]，将该测试样本从小到大排列，排列之后可见样本主要取值在第5～79个样本之间，舍去样本最大值，上界取第80个的样本值38，下界舍去前4个离散的小样本，取第5个样本值9为下界。改进样本边界(即减小样本上界，增大样本下界)后的拟合曲线与原样本边界(即取样本最大、最小值作为区间边界)拟合曲线对比如图12所示。

图12 黏聚力c样本拟合曲线对比Fig.12 Comparison of cohesion c sample fitting boundary

原样本边界下的正态信息扩散分布的拟合曲线边界为[1.47,48.53]，远超出样本边界；改进样本边界后正态信息扩散分布的拟合曲线边界为[3.47,43.53]，与样本值边界更接近。原样本边界下正态信息扩散分布的累积概率值为0.997 1，K-S检验值为0.048 3；改进样本边界后累积概率值为0.999 9，接近1，K-S检验值为0.050 9，小于临界值0.1511。

上文已说明，文献[16]提出的c3型区间确定方法下，拟合区间与实际样本区间不匹配，本文不再与之对比。为了进一步证明本文方法的有效性和普适性，对上文的内摩擦角和5组小样本为例，绘制样本拟合曲线对比图，如图13～18所示。区间取值和误差检验值如表5所示。

由图13～18及表5可见：收窄样本区间后，正态信息扩散分布不仅包络样本区间，且与样本的实际分布区间更接近；收窄样本区间后在满足拟合误差的前提下，截尾误差变小，样本累积概率值更逼近1。增大的误差来自拟合曲线的首、尾，实测样本在首、尾样本点分散，在绘制频率直方图时应在首尾处不等份分组，使样本首尾处的概率值逐渐减小趋于0。

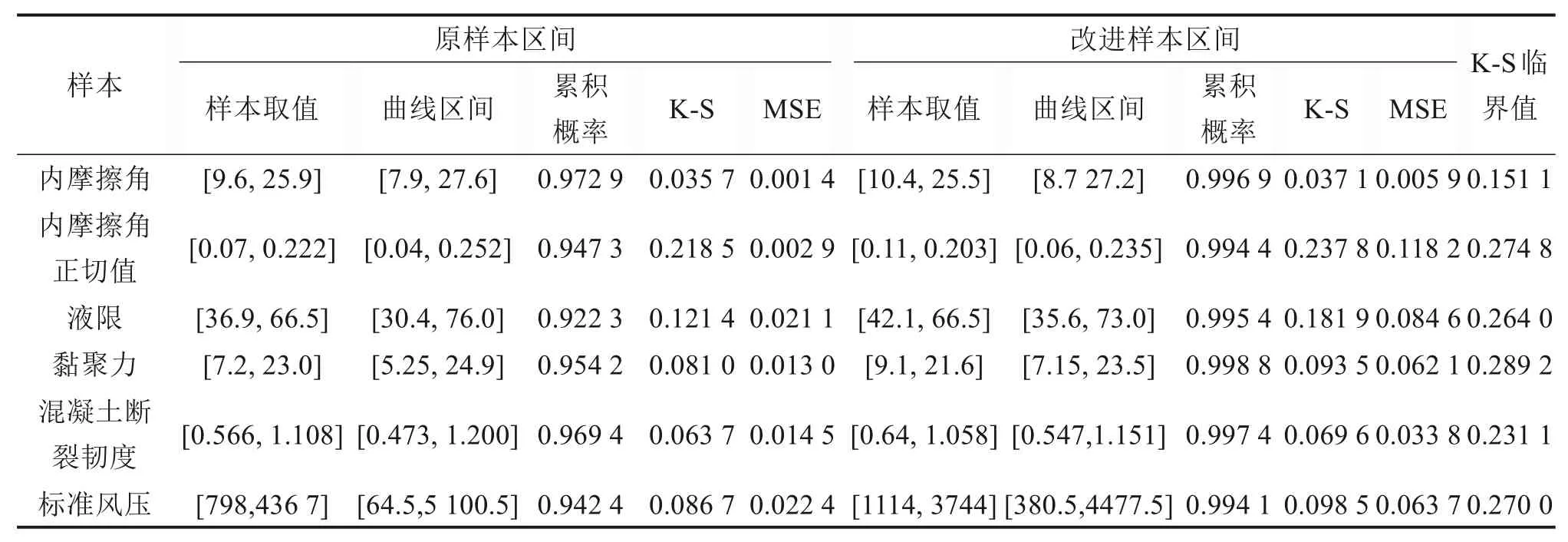
表5 样本边界、累积概率及误差检验统计值Table 5 Sample boundary,cumulative probability and error test statistics

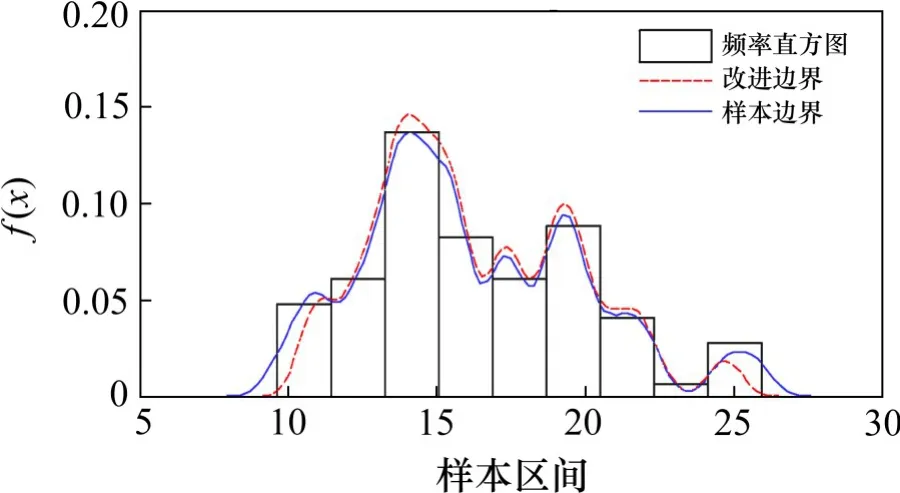
图13 内摩擦角样本拟合曲线对比Fig.13 Comparison of boundary fitting of internal friction angle samples

图14 内摩擦角正切值样本拟合曲线对比Fig.14 Comparison of fitting boundary of tangent value samples of internal friction angle

图15 液限样本拟合曲线对比Fig.15 Comparison of fitting boundary of liquid limit sample

图16 黏聚力样本拟合曲线对比Fig.16 Comparison of cohesive sample fitting boundary

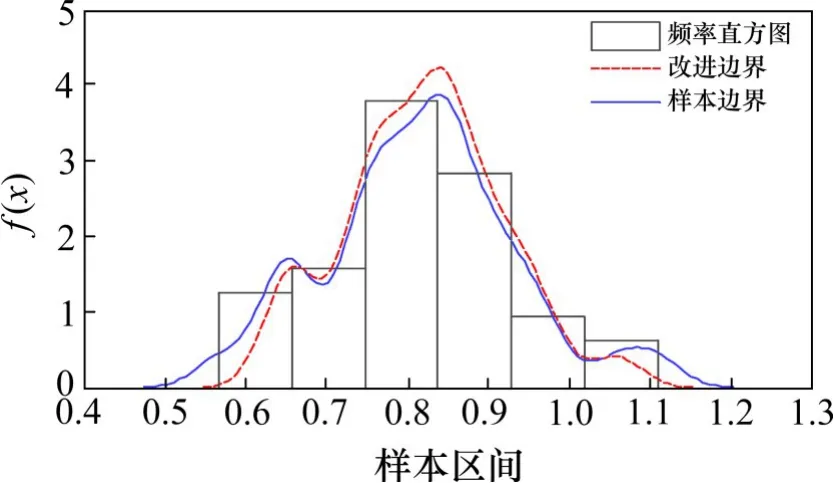
图17 350号混凝土断裂韧度样本拟合曲线对比Fig.17 Comparison of fitting boundary of No.350 concrete fracture toughness sample

图18 标准风压样本拟合曲线对比Fig.18 Comparison of fitting boundary of standard wind pressure samples

3 结论

1)合适的样本直方图分组是正态信息扩散法推断岩土参数概率密度函数的前提，测试样本直方图分组数越大，应采用较小的匹配窗宽；直方图分组数越小，应采用较大的匹配窗宽。在直方图分组数确定的情况下，以均方差最小为目标，逐步减小窗宽h的“匹配窗宽”确定方法简单有效。

2)提出的减小上界、增大下界的正态信息扩散分布样本边界确定方法，可有效减小正态信息扩散法推断岩土参数概率分布时出现的截尾误差问题。依据样本队列曲线，观测首尾样本点分布，可直观判定样本上界减小量和下界增大量。改进样本边界后的正态信息扩散分布区间内的累积概率更接近1。

正态信息扩散法的窗宽选择和截尾误差是研究人员无法回避的问题，本文的研究工作使窗宽选择和减小截尾误差问题又向前推进了一步，下一步将研究通过对大量岩土参数测试样本统计分析，探寻正态信息扩散法推断岩土参数概率分布中截尾误差取值的理论公式。