非线性滤波技术在GPS动态滤波中的运用

陈治国

(中国空空导弹研究院，河南 洛阳 471000)

0 引言

GPS全球定位系统为新一代的精密卫星导航定位系统，在军事、民用领域中均有广泛应用，但因GPS定位含有很多误差源，分别是测量随机误差与卫星的结合位置误差等，对定位精准性形成较大影响，GPS动态滤波是解除GPS定位随机误差额度有效方法之一。基于非线性滤波技术实现 GPS动态滤波，能显著提升 GPS导航定位的精准度。本文主要探究各种卡尔曼滤波方法在GPS定位估计方面的应用情况。

1 非线性滤波技术

1.1 扩展卡尔曼滤波

在上个世纪70年代后期，Sunahara等人专注于研究在非线性系统及观测下 Kalman滤波理论的扩展情况，明显拓展了 Kalman滤波的适用范畴。扩展卡尔曼滤波（EKF）是一种应用范围十分广泛的非线性系统滤波方程。为应对一些缺少相关原始状态信息与先验知识可供应用状况下的滤波，Fraser提出了信息滤波的概念，这种算法在处理测量更新问题方面表现出良好效能，但时间更新时需要进行大量的计算工作。

1.2 Unscented卡尔曼滤波（UKF）

EKF算法应用时暴露出两个不足：一是线性化假设不成立时，会造成滤波器十分不稳定；二是很难精准地计算出Jacobi与Hesse矩阵。为处理以上问题，国外学者提出了一种较适用于非线性系统的滤波器，即UKF。和EKF算法最大的不同是，UKF算法利用确定性采样所得的sigma点去表示系统额度属性，能做出更精准的估计结果。对于任何一个非线性系统，UKF算法对于高斯、非高斯输入量至少能分别达到最优估计的三、二阶近似，和EKF算法相比有很大提升[1]。

1.3 鲁棒滤波

常规Kalman滤波算法是基于H2估算准则为基础建设的，在现实运用中，很难全面了解外界干扰信号的统计属性，且系统模型本体存有一定摄动，实质上就是外界干扰与系统均带有不确定性。鲁棒控制就是针对如上特点，导入鲁棒控制思维，诱导鲁棒滤波理论的生成与发展过程，H∞滤波便是十分经典的方法。

2 GPS导航系统内非线性滤波技术的应用

2.1 EKF

2.1.1 技术处理

在卫星导航系统内，卡尔曼滤波是常用的定位解算算法，但真实系统的运动及观测模型都是非线性的，故而在现实运用中应用的是EKF。

2.1.2 仿真分析

观测时间间隔 T=l s，用户初始位置：（–1727947.4，4982862.9，3575658.9）m，初始速度：（100，100，100）m/s，初始加速度：（10，10，10）m/s2，三个方向的加速度正上、负下限分别取15 m/s2、–15 m/s2，应用二炮接收机实测仿真内的形成的卫星信息，求算出卫星位置[3]。

结合仿真结果，发现伴随抽样点位置的改变，真实值与估计值均有不断增加的趋势，滤波走势相对稳定后两条曲线基本吻合，显现出线性改变趋势。但在滤波早期，实际值和估计值之间形成较大偏差。在应用“当下”统计模型时，EKF算法在 X、Y、Z三个方向的最大定位误差依次是0.5008 mm、1.885 mm、2.278 mm，速度最大误差估计依次是2.064 m/s、5.821 m/s、6.777 m/s，均符合m级精准度要求。

2.2 UKF

2.2.1 UT变换

UT方法为UKF算法的核心。UT变化的思想主要是采用定量的阐述去进食一个高斯分布，和近似任何一个非线性函数或变换相比较其更加简单容易。其实现原理可以做出如下阐述：依照某个规则在原先状态分布内取一些点，使这些点的平均值、协方差和原状态分布的均值与协方差持平；把以上这些点代进非线性函数，这样便能获得非线性函数值点集，利用这些点集求算出变换以后的均值与协方差；因为以上所得的函数值未经过线性化处理，也没有重视自身的高阶项，故而基于此估计所得的平均值和协方差和EKF方法相比较精准度更高。

2.2.2 应用与分析

解读UKF算法对GPS系统动态滤波的仿真情况[4]。关于UKF算法三个方向的位置和速度误差对比的情况，发现UKF位置估计值自开始便和真实轨迹有较高的吻合度，表现出均匀增长的线性改变趋势。EKF、UKF算法三维位置估计的误差最大值以及位置误差样本标准差，如表 1。比较发现，在三个坐标方向的最大位置误差指标上，UKF都比EKF滤波提升了25%之上。对比两种算法的位置误差标准差，发现三个方向均有提升[5]。

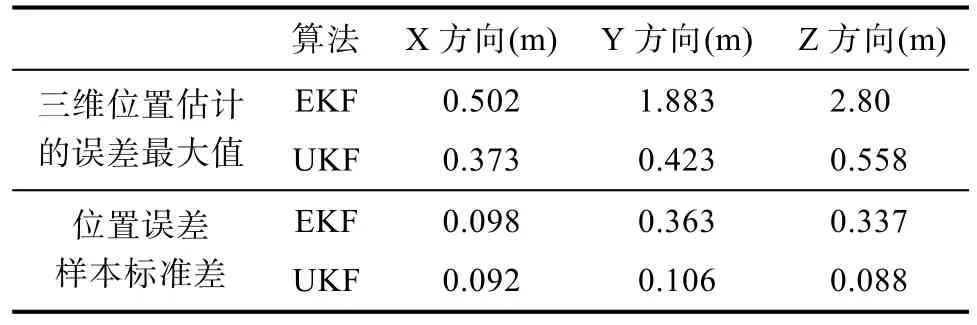
表1 UKF、EKF算法的应用情况Tab.1 application of UKF and EKF algorithms

基于以上仿真结果与分析说明，不难发现在非线性系统内，和EKF相比较，UKF的性能更加优异。UKF无需对状态及测量方程进行线性化近似处理，规避了非线性系统线性化过程生成的误差问题，且在计算量上和EKF没有显著差异。从某个角度分析，UKF能够将EKF取而代之用于非线性系统内。

2.3 H∞滤波

在上个世纪90年代，H∞滤波理论成为了鲁棒估计领域中的研究热点之一，其设计的主要思路如下：研发出一种滤波器，对应的性能指标是外界干扰信号到估计误差信号的H∞范数，这样当面对各种外界干扰信号时，能将估计误差值降到最低水平。

2.3.1H∞滤波问题的表达

本文主要研究最优H∞滤波的定义，具体是探寻到H∞估计，进而获得，推导出正定矩阵P0。参照以上做出的定义，不难发现H∞最优滤波器针对所有具有确定能量的可能干扰输入，确保将估计误差能量增益控制到最小。但以上所得结果过于保守，如下给出了次优H∞滤波问题的定义：具体是给定正数γ〉0，探寻到次优H∞估计

2.3.2 分析及应用

参照GPS导航系统状态方程与量测方程的计算方法，离散化以后，最后的状态及量测方法可以用式（5）表示：

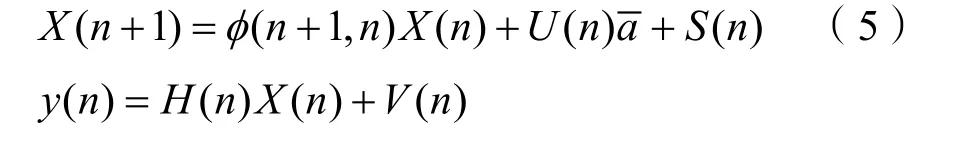
H∞滤波器设计阶段，伴随参数γ取值的减小，那么其所对应的H∞滤波器的鲁棒性就有一定强化；参数γ达最优值时，此时便能获得H∞最优滤波器，这种滤波器对外界干扰信号表现出很强的鲁棒性，但是其估计相对较保守，且只能在特殊情境下才能获得其最优闭环解。鉴于以上情况，通常利用探求其次优解的方式去代替。总结H∞滤波的仿真结果[7]，发现和UKF、EKF算法相比较，H∞滤波在三个方向位置最大误差是分别提升 90%、17%以上，且H∞滤波的收敛速度和其他两个算法相比较有很大提升。综合以上所得的仿真及分析结果，不难发现和UKF、EKF相比，H∞滤波能更好的修正GPS导航系统，位置与速度精准度均有显著提升，滤波误差收敛速度更快。并且不必实时计算系统噪声方差阵，降低了滤波的计算量，能取得更优秀的滤波效果[8]。

3 结语

当下，GPS导航系统在军事、民用等诸多领域中均有广泛应用，但是在部分场合，尤其是高动态环境下，初有的定位方法已经不能满足不断提升的性能要求。本文主要针对高动态用户设计定位算法，将卡尔曼最优估计理论用在GPS导航定位范畴中，明显提升了用户定位的精准性，使系统运行可靠性得到更大保障。和UKF、EKF相比，H∞滤波能更好的修正GPS导航系统，位置与速度精准度均有显著提升，滤波误差收敛速度更快。