基于Arnold置乱和DCT变换的彩色图像水印算法
2021-11-13冯和平王宽方李翠翠
冯和平,王宽方,李翠翠
(1.贵州水利水电职业技术学院,贵州 贵阳 551416;2. 贵州省大气探测技术与保障中心,贵州 贵阳 550001)
0 引言
随着计算机通信技术及多媒体存储和传输技术的发展,数字文件的复制变得非常容易,同时,数字信息持有者的版权保护问题和盗版问题也变得愈来愈严重。数字水印技术自被提出以来,由于数字水印技术在信息安全和经济上的重要地位,发展较为迅速,其在数字产品知识产权保护方面的作用也越来越重要。本文结合Arnold置乱和 DCT变换技术提出了一种新的基于非等长置乱水印算法,将水印信息进行预处理嵌入到载体图片的频域中,保证水印不可见性的同时,也提高了水印的抗干扰性[1-5]。
1 水印信号的产生
数字水印技术就是通过一定的算法将一些标志性信息直接嵌入到多媒体内容当中,但是不能影响原始内容的价值和使用,且不能被人的感知系统觉察到。当然,水印在一定的干扰下会受到破坏,为了给攻击者增加去除水印的难度,目前大多数水印制作方案都采用密码学中的加密体系来加强,在水印嵌入和提取时采用一种密钥,甚至几种密钥联合使用。
本论文原水印图片采用大小为 160×120的图片,将其二值化后再转换成140×140的图片,数据不足部分用0或1填充,然后对140×140 矩阵进行Arnold变换,达到置乱水印的目的,置乱后再对置乱信息分解成160×120和20×20两部分信息,即为水印信息。水印信号生成框图如图 1,其中置乱次数作为一种密钥。水印信号生成的matlab仿真结果如图2。
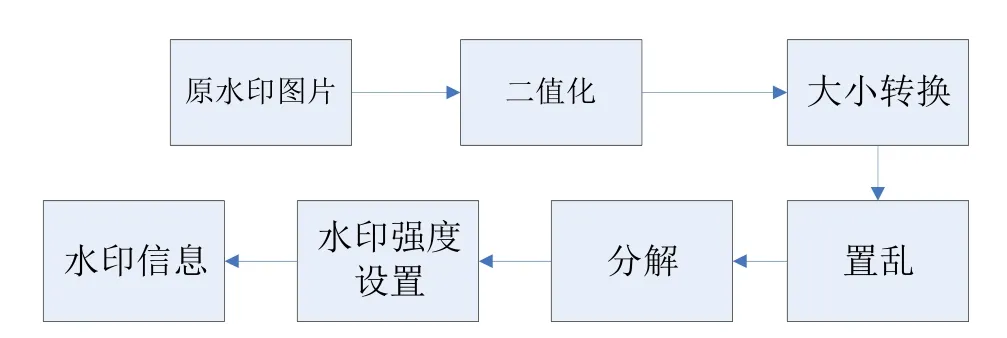
图1 水印信号生成框图Fig.1 block diagram of watermark signal generation
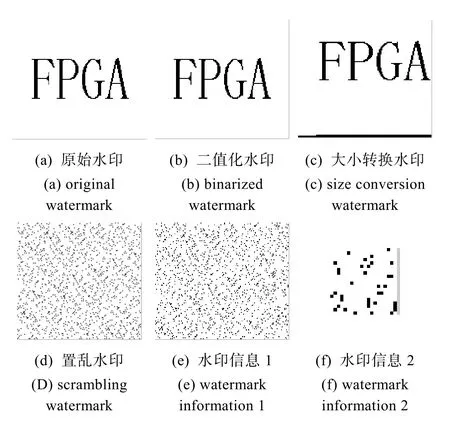
图2 水印信息仿真结果图Fig.2 simulation results of watermark information
2 水印算法
数字水印系统包含水印的嵌人和水印的检测与提取两个方面,水印的嵌入就是将水印信息按照事先约定好的位置嵌入到原始数据中[6]。水印信号检测和提取是指按照水印嵌入思想判断某一数据中是否含有指定的水印信号并提取出水印信号的过程,本设计是在DCT变换域嵌入置乱后的水印信息,为减少计算量,本论文只是抽取部分数据进行DCT变换,再将水印信息嵌入到频域系数中。其嵌入和提取流程图如图3。
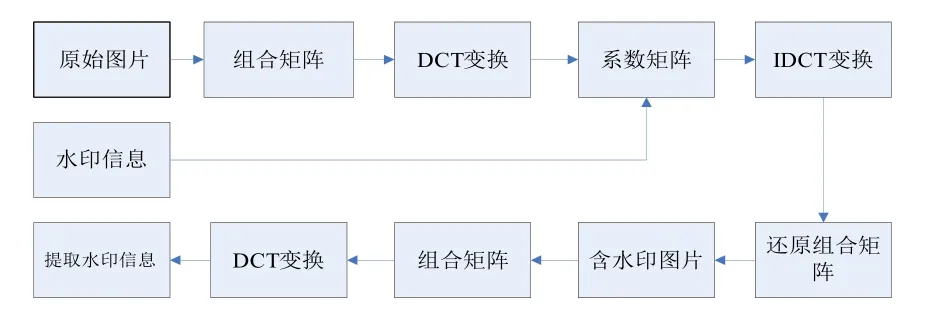
图3 嵌入和提取流程图Fig.3 flow chart of embedding and extraction
2.1 水印的嵌入算法
将置乱分解后的水印信息嵌入到彩色图片中,具体思路如下:首先分解出原始图片的RGB三个分量,分别提取三个分量数据的低两位,低三位,低三位。其次将提取出的两位、三位、三位重新组合成一个8位数组,对新数组进行DCT变换得到变换后的系数,按照预先规定的位置将水印信息嵌入到系数矩阵中,再对嵌入后的矩阵进行反DCT变换即得到组合矩阵。最后将含水印的组合矩阵拆分再还原到 RGB中即得到含水印的图片[7]。
为了保证水印的不可感知性和减小计算所带来的误差,假设M是二值矩阵,大小为M1×M2,则M= {m(i,j) , 0 ≤i<M1,0 ≤j<M2}其 中 :m(i,j)是水印像素点(i,j)的强度。将m(i,j)的取值变换为单极式m(i,j)∈ ( 0,ħ),其中ħ为正整数。最后通过实验选取最佳ħ值。
水印嵌入算法的matlab仿真结果如图4。图4为不同水印强度嵌入在低中高频域中的效果图。实验结论:嵌在低频时,水印强度越大,不可见性越差,同理可以把水印嵌入在中频和高频,有实验得知:同样强度下,嵌在高频的不可见性最好,低频的不可见性最差。

图4 水印嵌入在低中高频的效果图Fig.4 effect picture of watermark embedded in low,medium and high frequency
2.2 水印的检测算法
本检测算法采用盲提取,提取方法如下:将含水印图片的RGB分解出来,分别提取三个分量的低二、三、三位组成一个8位的新数组,对新数组进行DCT变换,然后按照预先规定的位置将水印信息提取出来,提取过程中要设定一个阀值,若提取的值大于阀值则将其变为 1否则变为 0,其中水印的嵌入位置可作为一种密钥[8-10]。原水印和在不同强度下阀值设定在强度的一半低频嵌入提取水印效果图如图5。

图5 原水印和在不同强度下低频嵌入提取水印效果图Fig. 5 the original watermark and the effect of low-frequency embedding and extraction of watermarks under different intensities
由实验可知,提取的水印和强度有关,在此用水印误差σ作为一种衡量标准,σ=L/N,其中L为提取水印与二值化水印像素值不同点的个数,N为二值化水印像素值总数。误差统计表如表1。
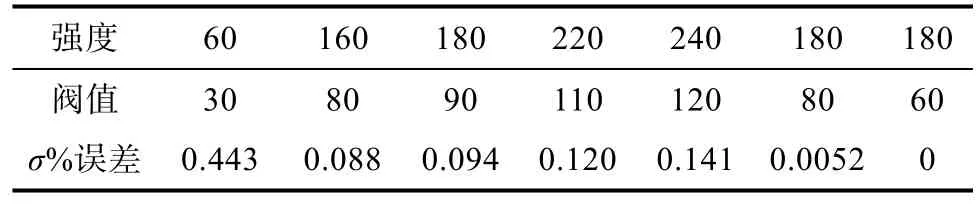
表1 不同情况误差统计表Tab.1 error statistics table for different situations
3 结论
本设计实现了基于Arnold置乱和DCT变换的嵌入和提取方案,由matlab仿真结果可知:该方案不影响原内容的价值和使用,具有较好的鲁棒性和不可见性,且该方案采用非方阵变换后嵌入,和以前的直接嵌入水印算法相比具有更好的防篡改性,且采用两种密钥给攻击者增加了去除水印的难度。
