一类非局部高维抛物系统解的爆破分析

欧阳柏平，肖胜中

（1.广州华商学院数据科学学院，广东广州 511300；2.广东农工商职业技术学院，广东广州 510507）

考虑下面反应扩散系统解的全局存在性和爆破问题

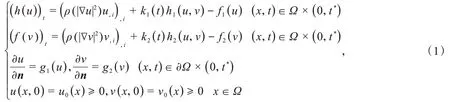
其中，Ω是Rn(n≥3)中具有光滑边界∂Ω的一个有界凸区域，▽是梯度算子，t*＜∞是爆破发生时间，否则表示u，v在∂Ω上的外法向量导数.

近几十年来，有关反应扩散问题解的爆破研究已经有很多的成果［1-12］.早期的成果其研究的边界条件和空间维数主要是齐次和Robin边界条件以及R3空间.之后，有学者把边值条件推广到一般的非线性边界条件下分析.随着研究的进一步深入，具有时变或空变系数的局部和非局部反应扩散方程和系统解的爆破问题成为了目前的研究热点.一般而言，研究其解的爆破和不爆破等性态问题必须处理好初边值条件、空间维数、时变或空变系数、局部或非局部项以及非线性项等要素.近年来，由于非局部的反应扩散问题比局部的情况更接近实际，因而其解的爆破研究更受学者们重视.但是由于局部的反应扩散理论和方法不能直接用于非局部情况，因而存在不少困难.有关解的上下界的估计，目前上界的估计方法较多，而下界的方法较少.在实际中，当爆破发生时精确的推出解的爆破时间是非常困难的，故将问题转化为估计解的爆破时间的上下界.在应用数学领域，下界的研究是一个很重要的方向，其应用已经涵盖天文、物理、化学、生物、航天等领域［13-14］.

文献［1］研究了如下反应扩散方程解的爆破问题

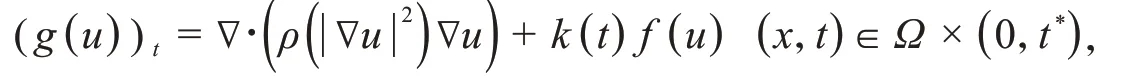
运用最大值原理和相关的微分不等技巧，得到了Robin条件下解的爆破和不爆破条件以及爆破发生时解的爆破时间的上下界估计.

文献［2］研究了如下反应扩散抛物系统爆破问题

在非线性边界条件下作者得到了高维空间上解的爆破条件以及爆破发生时解的爆破时间的上界和下界估计.

文献［10］考虑了如下反应扩散方程解的爆破现象

其中，Ω⊂Rn n≥1.运用相关的微分不等式技巧得到了全空间上解的爆破时间的下界估计.

文献［11］研究了如下具有时变系数的弱耦合反应扩散系统解的爆破问题

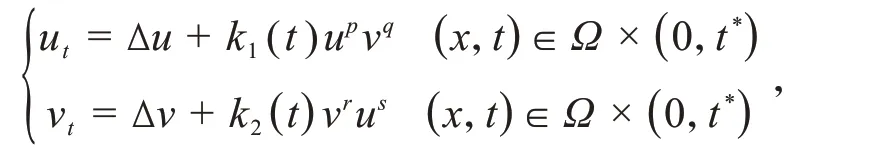
Dirichlet边界条件下，推出了解的爆破条件同时得到了在2种不同测度下Rn n≥3上解的爆破时间的下界估计.

受以上文献的启发，研究问题（1）在非线性边界条件下Rn n≥3上解的全局存在性和爆破发生时爆破时间界的估计.目前为止，尚未有论文研究关于问题（1）的非局部反应扩散系统解的爆破问题.旨在希望通过构造恰当的能量泛函辅之以适当的约束条件合理的处理高维空间、时变系数、非局部项、吸收项以及非线性边界条件等对解的爆破影响.

1 预备知识

引理1［9］设Ω是Rn n≥3上的有界凸区域，则对于u∈C1(Ω)，s＞0，有

其中，

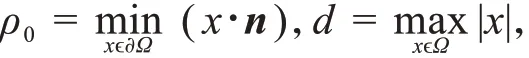
其中，dA表示面积元.

引理2［15］Sobolev不等式

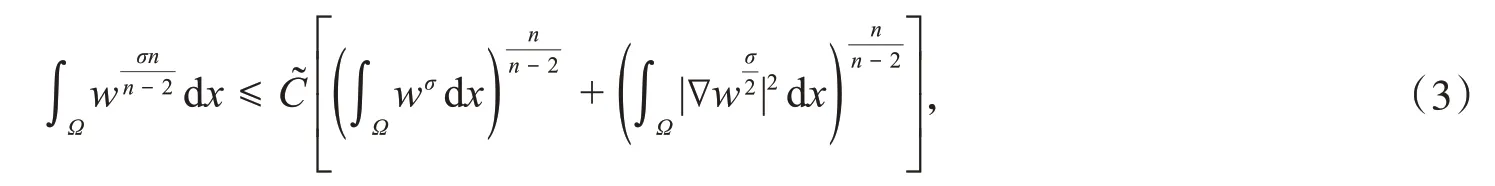
2 爆破时间的下界

设

其中，l

另外假设函数f i(ξ)，g i(ξ)，ρ(|▽ξ|2)i=1，2满足以下兼容性条件

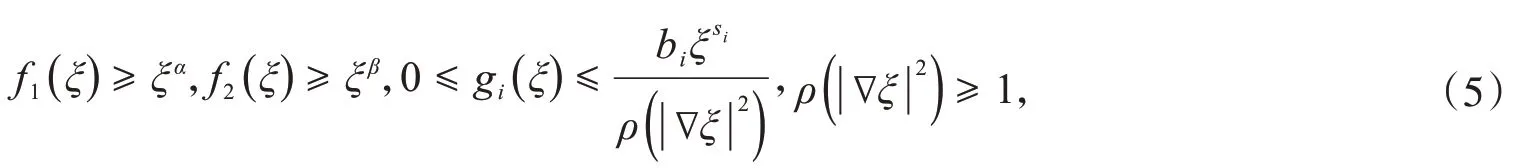
其中，ξ≥0，s i＞1，α＞2s1-1，β＞2s2-1，b i＞0.

结论：

定理1设u(x，t)，v(x，t)为问题（1）和式（4）～（5）在有界凸区域Ω的经典的非负解，则式（4）定义的能量泛函满足

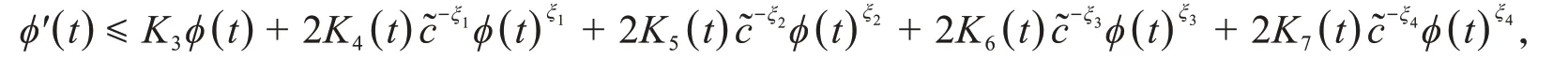
由此推出爆破时间t*的下界估计为

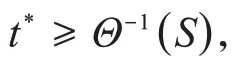
其中，K3，K i(t)i=4，5，6，7，ξi i=1，2，3，4，c~，Θ均在后面定义，Θ-1为Θ的反函数.

证明对式（4）中φ(t)求导数且利用式（5），可以推出

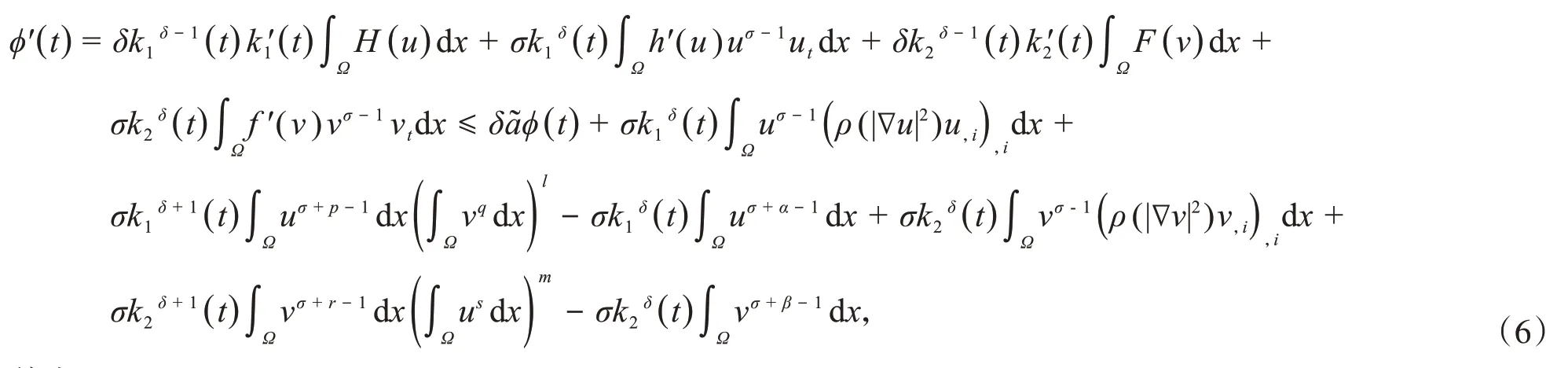
利用Hölder不等式和Young不等式，散度定理和式（5），可以推出

由式（7），可得

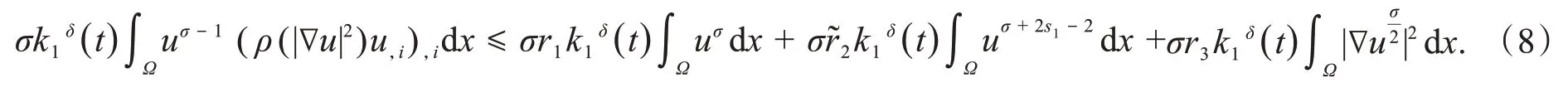
类似的推导，有

将Hölder不等式和Young不等式应用于式（6）右边第三项和第六项，分别得

将式（8）～（11）代入到式（6），得到

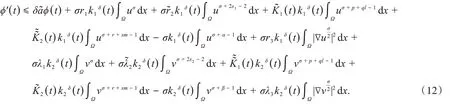
对于式（12）右边第三项和第九项，由Hölder不等式和Young不等式，有

又由式（4）～（5）可知，

结合式（12）～（15），得到

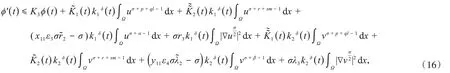
选择合适的ε3，ε4，使得于是，有

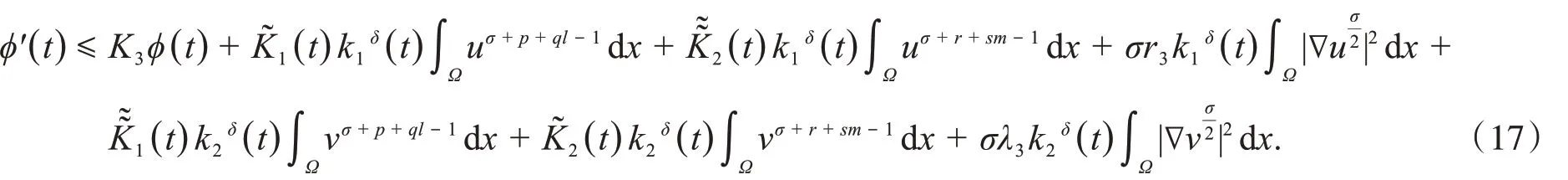
对于式（17）右边第二项，利用式（3）以及Hölder不等式和Young不等式，可以推出

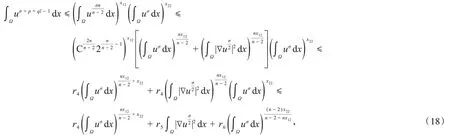
同样可得，

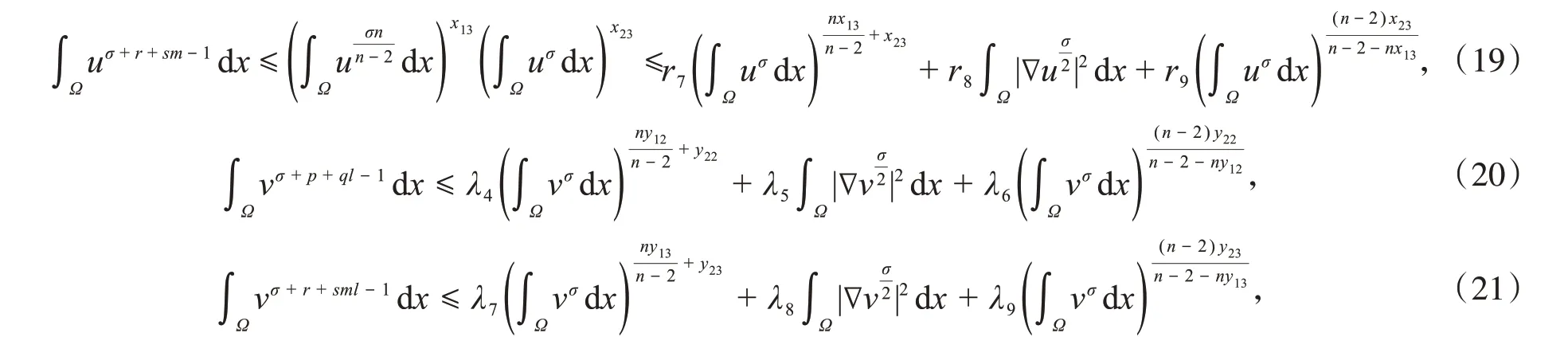
联立式（17）～（21），可以推出

其中，

选择合适的ε1，ε2，ε5，ε6，ε7，ε8，使得M1≤0，M2≤0.结合式（15），有

设

其中，K(t)=1+K4(t)c~-ξ1+K5(t)c~-ξ2+K6(t)c~-ξ3+K7(t)c~-ξ4.

对式（23）从0到t*积分，可得

又ξi＞1i=1，2，3，4，所以式（25）右边积分存在.由式（24）Θ(t*)定义易知其为单调递增函数，故

其中，Θ-1是Θ的反函数.

证毕.

3 爆破时间的上界

设

其中，p，r＞1，l，m≥0，0≤h(ξ)≤ξ，0≤f(ξ)≤ξ，ξ≥0.

定理2设u(x，t)，v(x，t)为问题（1）和式（27）在有界凸区域Ω的经典的非负解.函数f i(ξ)，g i(ξ)，ρ(|▽ξ|2)，k i(t)i=1，2以及φ(0)满足如下兼容性条件0＜f1(ξ)≤ξα，0＜f2(ξ)≤ξβ，ρ(|▽ξ|2)≥0，g i(ξ)≥0，ξ≥0，p＞

则式（27）中定义的能量泛函满足

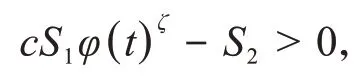
从而可得爆破时间t*的上界为

证明由式（27），利用散度定理，Hölder不等式和Young不等式以及式（28），对φ(t)求导数，得

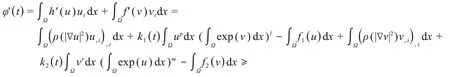
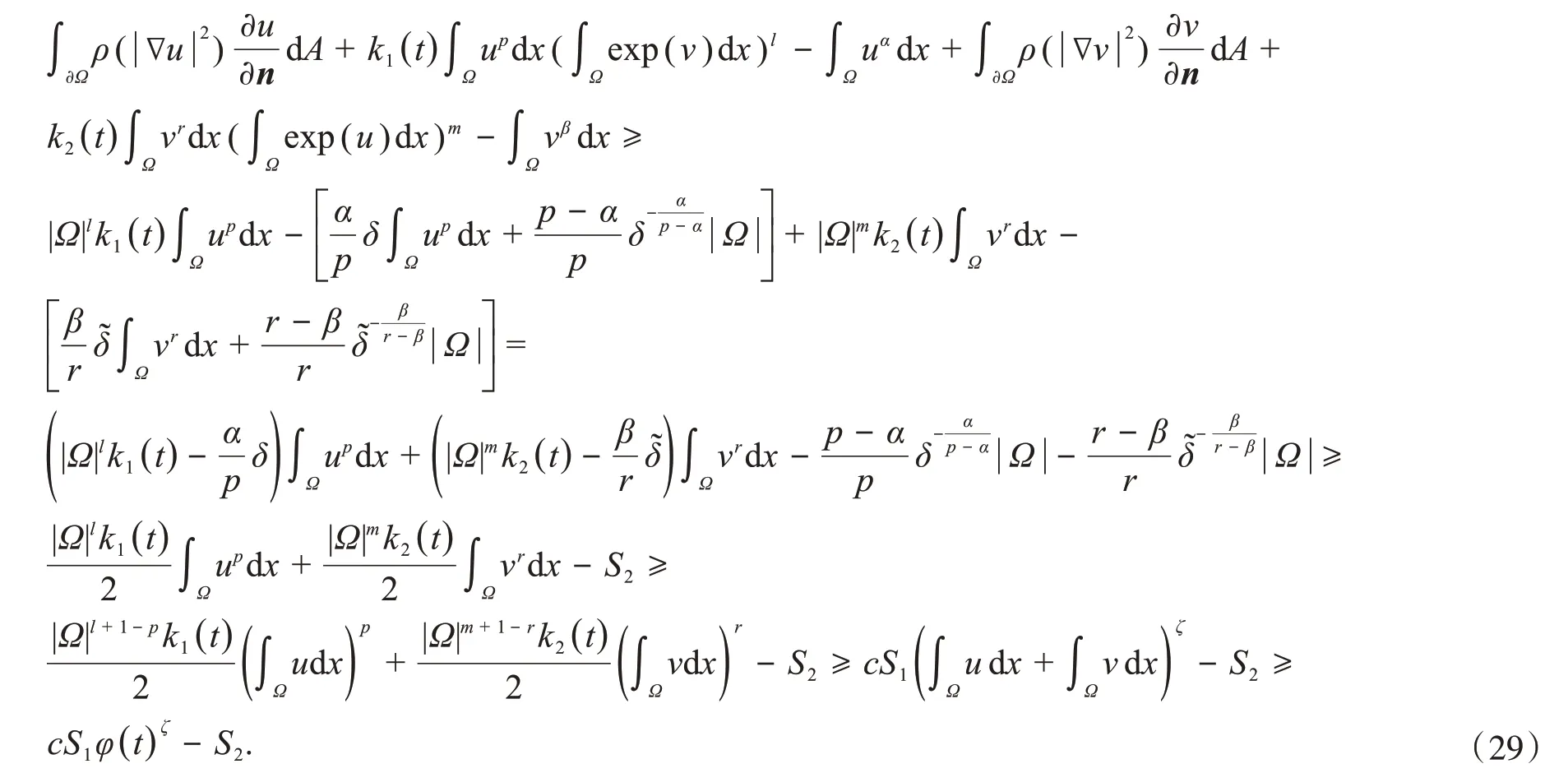
又由式（28）可以推得，∀t≥0，有

事实上，取

则有

从式（29）和（32）可知φ'(t)＞0 0＜t＜t1.从而有，φ(t1)＞φ(0).故c S1φ(t)ζ-S2＞0，矛盾.

从0到t积分式（30），可得

式（33）表明φ(t)测度下u，v会在某个时刻t*爆破，也就是说，

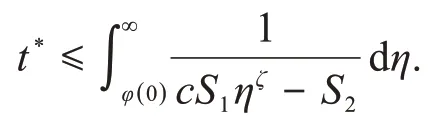
若u，v在φ(t)测度下在某个时刻t*不发生爆破，则

由此可推出

当t→+∞时，式（34）两边取极限，得到

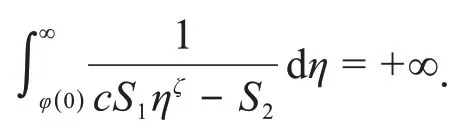
这是一个矛盾.

故φ(t)测度下u，v的上界估计如下

4 全局存在性

设

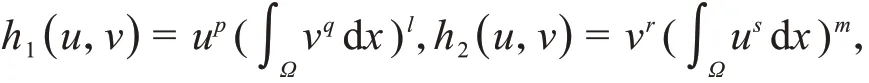
定 理3若u(x，t)，v(x，t)为 问 题（1）和 式（36）在 有 界 凸区 域Ω的 经 典 的 非 负 解.函 数f i(ξ)，g i(ξ)，ρ(|▽ξ|2)i=1，2满足以下兼容性条件

其中，ξ≥0，b i＞0，s i＞1，α＞max{2s1-1，p+ql，r+sm}，β＞max{2s2-1，p+ql，r+sm}，则φ(t)测度下问题（1）的解在任何有限时间都是有界的，也即问题（1）的解是全局存在的.

证明对φ(t)求导数，得

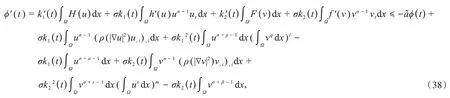
其中，=min{a1，a2}.

估计式（38）右边的第二项和第五项.利用式（7）～（9）推导，易得

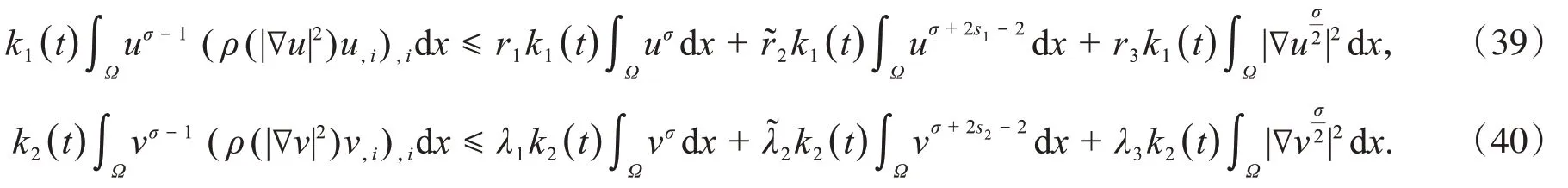
取恰当的ε1，ε2，使得r3≤0，λ3≤0.联立式（38）～（40），有

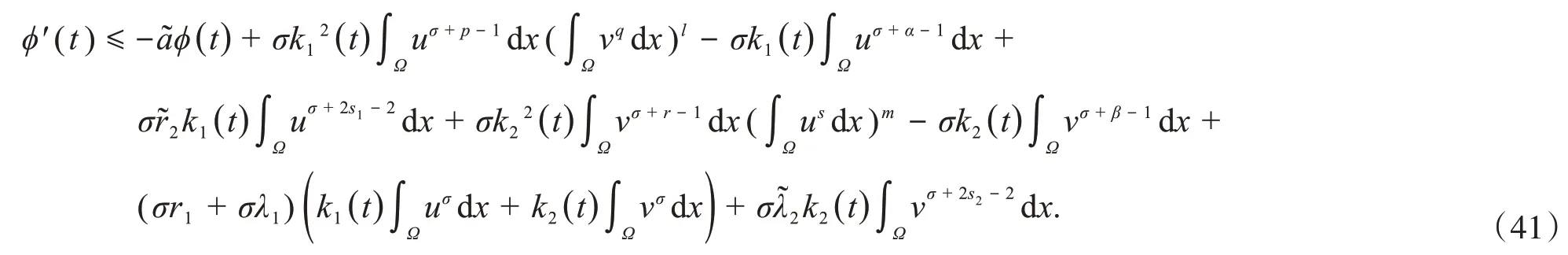
又由Hölder不等式和Young不等式，可以推出

取ξ=max{p+ql，r+sm，2s1-1}，ζ=max{p+ql，r+sm，2s2-1}，将式（42）～（43）代入到式（41），得到

对于式（44）右边第一、二、四项，利用Hölder不等式，可以推得

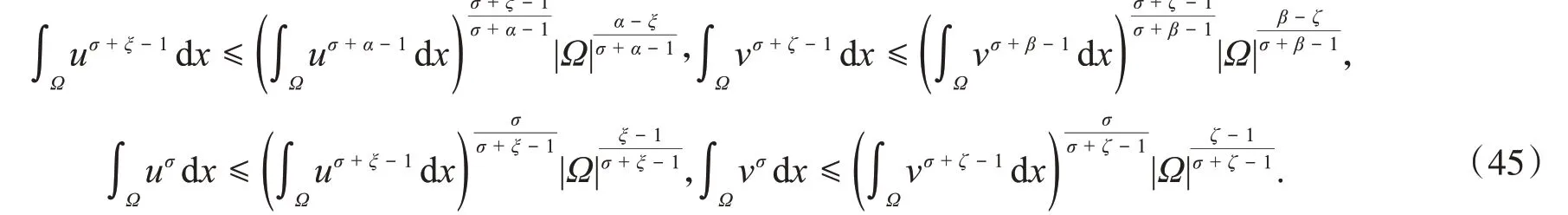
由式（44）～（45），有

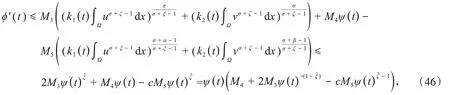
利用式（45），易得

又由式（36）～（37），可得

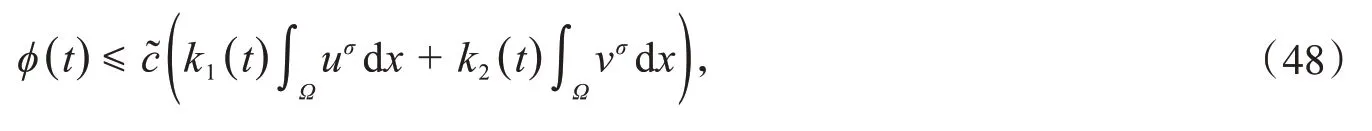
其中，~=max{c1，d1}.

结合式（46）～（48），可以推出

又因为1-ξ~＞0，ζ~-1＞0，所以由式（49）易推知在φ(t)测度下u，v是全局存在的.实际上，假设存在某个t*爆破，也就是

由式（49），得φ'(t)≤0，∀t∈[t0，t*).由此得到φ(t)≤φ(t0).当t→(t*)-时取极限，有

矛盾.

证毕.